基于贝叶斯分类的变压器绕组故障诊断算法

2021-07-07李学生张尊扬

济南大学学报（自然科学版） 2021年4期

李学生，张尊扬

(北方民族大学电气信息工程学院，宁夏银川 750021)

现代社会的日常生活、生产与电能息息相关，一旦发生电力事故，就会给人们的生产、生活造成诸多不便，甚至会带来严重的安全问题和巨大的经济损失[1]，因此，对电力系统传输的可靠性要求越来越高。变压器作为电力系统最重要的部分之一，其安全、稳定运行是保证整个电网安全运行的基础。自然灾害、人为操作不当及高温、高压作用下绝缘体老化等都可能成为导致变压器损坏的直接原因，而且通常情况下变压器故障的严重程度和性能恶化是逐渐发生的，最终可能导致电力系统大面积崩溃，引发停电[2]。由于绕组是变压器中最容易发生故障的部位，因此对变压器绕组故障的诊断变得尤为重要。

文献[3]中通过分析脉冲信号的传播过程，构建变压器绕组分布参数电路模型，得到绕组故障后波阻抗的变化规律，通过变压器绕组及绕组故障后特性曲线，判断绕组是否发生故障，由此实现变压器绕组匝间短路故障诊断。该方法的故障识别率较高，但故障诊断时间较长。文献[4]中采集变压器绕组振动信号，构造双天线无源射频识别(RFID)振动传感器标签，根据变压器绕组振动信号特点，采用奇异熵降噪处理原始信号，实现变压器绕组故障的在线诊断。该方法能够准确地定位故障，且功率损耗及成本较低，但故障诊断准确率较低。

针对上述问题，本文中提出基于贝叶斯分类的变压器绕组故障诊断模型，利用贝叶斯理论进行故障分析，通过电场分布和电场能量计算出导体间的互电容之和，获得电感和电阻矩阵，将绕组电感和电阻作为贝叶斯理论的基础，得到变压器绕组故障特征量；采用欧拉非线性理论模型离散处理五阶故障模型，构建故障模型的输出方程，完成变压器绕组故障诊断。

1 变压器绕组故障特征量

变压器种类较多，按照相数区分可分为三相变压器和单相变压器，按照绕组结构又可分为双绕组变压器和三绕组变压器。单相双绕组变压器发生短路时状态如图1所示。

从图1(a)可以看出，当绕组1或绕组2发生匝间短路时，均可以将短路的Nk视为第3绕组。图1(b)所示为第3绕组短路时具体状态。图中Rg表示故障点弧光电阻，大小与电弧路径、短路电路、温度等相关。研究表明，当电弧压降Ug=50～150 V时(一般取75 V)，第3绕组的额定电压U3W可以表示为

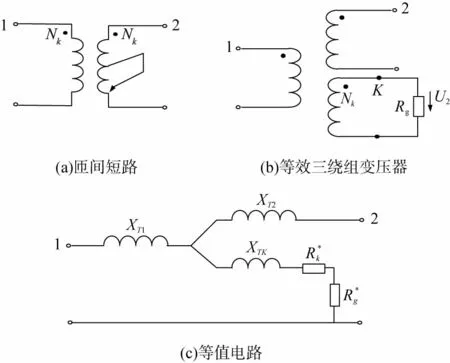
1、2—绕组编号。图1 变压器匝间短路及其等值电路

(1)

式中：UW为短路侧变压器的额定电压；W为绕组原有匝数；α为短路匝数，α=0～1。

(2)

式中：I3W为等值的第3绕组额定电流；sW为变压器额定容量。

变压器匝间短路等效电路3个绕组的等效电抗XT1、XT2、XTK的计算公式分别为

(3)

式中XK12、XK1K、XK2K分别为绕组1和绕组2、绕组1和Nk、绕组2和Nk之间的短路电抗。若短路匝数较少，XK12可以选用铭牌值。若短路匝数与绕组2的总匝数一致，则说明变压器的一侧发生了短路。

变压器中的各个绕组都可以视为由电阻、电容、电感3个特征量组合而成的一个网络，因此，以上3个参数都能够反映绕组的自身结构、组间结构、绕组与箱体或铁心之间的状态等情况。若绕组受到严重的短路冲击后产生严重变形或发生较大位移时，其电阻和电感就会产生较大变化，也就是说，如果发现变压器的绕组的电阻和电感参数发生明显变化，说明该绕组有极大可能发生了故障。

根据平行板电容理论[5]对电容进行计算。平行板电容器是在2个相距很近的平行金属板中间夹一层绝缘物质——电介质，从而组成的一个最简单的电容器，是最基本的电容器，现阶段使用的绝大多数电容器均是根据平行板电容器变形而来的。当电容器两板间距离发生改变、错开正对面积或两板间加入电介质时，电容器极板上所带的电量不发生变化，因此电容C计算公式为

(4)

式中：ε0为电容器的介电常数；εp为绕组绝缘处的介电常数；da为绕组平均直径；h为导线内金属的净高度；ap为绕组绝缘厚度。

假设系统中含有m根多导体传输线，对第k根导体进行考察，则

qk=Ck,1Uk,1+Ck,2Uk,2+…+Ck,mUk,m+Ck,0Uk,0，

(5)

式中：qk为第k根导线的电荷量；Ci,j(i≠j，i,j=1,2,…,m)为导体间互电容；Ui,j(i≠j，i,j=1,2,…,m)为电位差；Ck,0为导体对地电容；Uk,0为导体对地电位。

如果忽略掉电介质随电频变化而产生的细微改变，则绕组导体间的电容与介电常数及绕组的形状和位置相关，与绕组自身电压无关。当变压器二次电压有效值Uk=1 V，并且发生绕组接地的情况时，产生的静电场能量Wεk为

(6)

利用电场分布和电场能量即可计算出导体间的互电容之和。对导体进行加压，获得电容的线性方程组，对其进行求解即可得到电容矩阵。

变压器绕组电感L分为2个部分：一部分为线圈导线外自感，该部分参数定义为Ln;另一部分为线圈导线内自感，该部分电感参数定义为Li，即

L=Ln+Li。

(7)

求解Ln时，假设绕组为传输线，根据多导体传输线理论[6]可得

(8)

式中：C0为电容矩阵；E为单位矩阵；v为真空电磁波传播速度；μ0为电容器的磁导率。

高频集肤效应[7]引起的绕组1内自感L1表示为

(9)

式中：Rs为集肤电阻；f为频率。

考虑高频情况下的集肤效应，则

(10)

式中：d1、d2分别为导线金属芯直径、包括外绝缘层的导线总直径；μ为磁导率；σ为电导率。

电导参数能够表达电容的损耗，把绕组之间的电容Cd视为电阻电容的并联支路[8]，则

Cd=2πfCtanδ，

(11)

式中δ为阻抗角。

根据平行板电容理论，上述步骤能够计算电容器极板上所带电量，利用电场分布和电场能量，计算导体间的互电容之和，将绕组之间的电容视为电阻电容，从而获得变压器绕组故障特征量。

2 基于贝叶斯分类变压器绕组故障诊断模型

贝叶斯原理[9]包含先验概率和后验概率2个关键因素，是指在情报不完全的情况下，对未知状态部分采用已知的条件概率密度参数表达式和先验概率进行估计，然后利用公式将发生概率转换成后验概率，并且对其进行修正，最后利用后验概率的大小进行决策分类的过程。本文中利用贝叶斯理论，分析变压器绕组故障，也就是利用已知的检测目标故障特征量，通过相关函数判定变压器绕组是否发生故障的一个分类过程。

假设实例数据集合D={X1,X2,…,Xn,M}为离散随机变量的有限集，其中X1,X2,…,Xn为属性变量，M为类变量，取值范围为{c1,c2,…,cm}。设xi为属性Xi的取值，则实例Ii=(x1,x2,…,xn)属于类bj的概率，由贝叶斯定理可表示为

λP{bj}·P{x1,x2,…,xn|bj}P{bj}，

(12)

式中：λ为正则化因子；P{bj}为先验概率；P{bj|x1,x2,…,xn}为后验概率，其数值能够反映样本内数据对bj的影响。

式(12)可以转化为

P{bj|x1,x2,…,xn}=

(13)

在基于贝叶斯的故障分类过程中，各个特征量是完全独立的[10]，当样本集D中各个类别都相对齐全时，通过对所有故障的发生频率的计算，就可以获得特征变量的条件概率P{xj|B}，其中B为第j类故障样本数，同时获得各个特征量的概率P{B}，从而完成分类学习，即

(14)

(15)

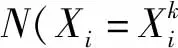
(16)

由于贝叶斯故障特征变量和类别量之间是相互独立的，因此，式(16)也可以表示为

(17)

将2个二次绕组折算到一次绕组的三阶精确数学模型可以表示为

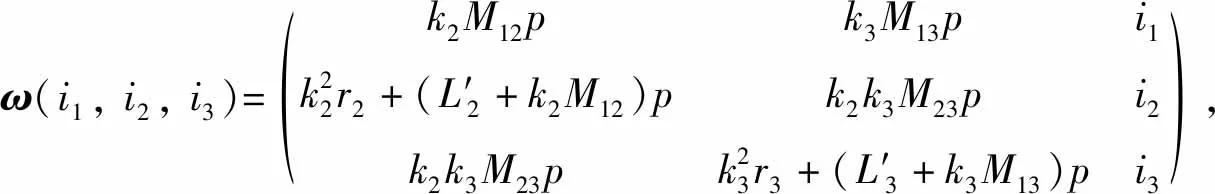
(18)

将式(18)的三阶矩阵进行整理，用电感、电阻表示为

Fpi=-Ri+u，

(19)

式中：F为电感矩阵；R为电阻矩阵；i为电流矩阵，i=(i1,i2,i3)T；u为电压矩阵，u=(u1,u2,u3)T。

电感矩阵F和电阻矩阵R也可以表示为

(20)

取状态变量x1=i1,x2=i2,x3=i3,，考虑到变压器的各类绕组故障均可以反映在电阻中，如果分别对一次、二次回路电阻r1、r2进行监控，则取附加状态变量x4=r1,x5=r2。同样，对电感进行相同处理，取状态向量xe=(x1,x2,x3,x4,x5)。通过欧拉非线性理论模型离散[11]对式(18)进行处理，可得五阶故障模型

xe(k+1)=xe(k)+Tsg[xe(k),u(k)]，

(21)

式中：Ts为采样周期；定子绕组暂态

(22)

将式(22)中的电阻矩阵监控参数r1、r2转换为状态变量x4、x5，得

(23)

电压信号可表示为

u=2U1Wsinθ，

(24)

则故障模型的输出方程为

y(k+1)=Hx(k+1)+e(k+1)，

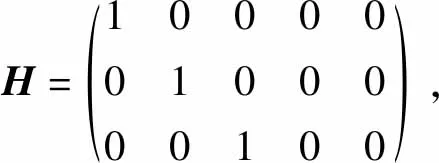
(25)

式中e(k+1)为协方差为R′、均值为0的测量噪声。

通过上述步骤，采用条件概率密度参数和先验概率估计未知状态，修正发生概率转换后的后验概率，利用后验概率决策分类，通过欧拉离散获得五阶故障模型，构建故障模型的输出方程，从而完成基于贝叶斯分类的变压器绕组故障诊断。

3 仿真结果

为了验证所提方法的有效性，搜集整理出200个变压器绕组故障数据，分别为绕组匝间短路故障60个、绕组接地故障80个、绕组变形故障60个。从中选取100个样本作为训练集，50个样本作为测试集进行实验验证。分别对比采用文献[3]、文献[4]中的方法与本文中提出的方法诊断变压器绕组故障的性能，结果如表1所示。从表中数据可以看出，在50个变压器绕组故障样本中，本文中提出的方法诊断出48个故障样本，准确率高达96%，故障诊断效果较好。

表1 不同方法的故障诊断准确率

为了验证该方法对不同故障诊断的时效性，选取绕组匝间短路和绕组变形2种故障类型进行比较，结果如图2所示。从图中可以看出，对匝间短路、绕组变形故障进行诊断时，模型仅分别延时4、4.3 s就诊断出绕组存在故障，可见该方法针对不同类型的故障诊断时间较短，诊断效率较高，达到了对变压器绕组故障的快速诊断的目的。