基于分层粒子群优化的三维点云配准
2021-07-07黄筱佟温佩芝萧华鹏邸臻炜
黄筱佟,温佩芝,萧华鹏,贺 杰,邸臻炜
(1.梧州学院 a.广西高校图像处理与智能信息系统重点实验室,b.大数据与软件工程学院,广西 梧州 543002;2.桂林电子科技大学 计算机与信息安全学院,广西 桂林 541004;3.广西师范大学 物理科学与技术学院,广西 桂林 541004)
随着图像技术的发展,借助图像数据挖掘获取有价值数据的方法在多个行业广泛应用,并且取得了良好的效果。当前的图像数据研究多是基于二维的,三维图像的研究主要集中在图像的建模和重构,摄像机从不同角度对同一实体拍摄图像数据,根据这些图像还原实体空间结构[1]。由于拍摄时受到背景、光线和噪声等的影响,因此根据多张二维图像重构三维实体的过程并不简单。当前三维图像重构采用的主要手段为三维点云配准,即通过摄像机对实体表面的多角度二维图像的采集,获得图像点云,根据二维图像所包含的点云RGB三原色和坐标值、点云与摄像机的距离值[2]等获取三维实体有效特征,去除多个二维图像包含的冗余特征,将多个图像点云平移变换至同一坐标系。
对于三维点云配准的研究成果较多。文献[3]中采用八叉树实现大规模点云样本的配准,点云的坐标变换结合了邻居节点拓扑。文献[4]中将遗传算法运用于点云配准,并运用熵值计算点的关联性,两者均取得了较好的配准效果。在小规模的点云数据匹配过程中,迭代最近点(iterative closest point,ICP)算法可以获得较好的匹配准确度,而且效率较高[5]。由于在进行较大实体的重建过程中,需要处理数量庞大的数据点云配准,标准ICP算法会消耗大量的配准时间,因此,本文中在标准ICP算法的基础上,引入分层粒子群优化 (PSO)算法,以提高配准的效率。
1 ICP 算法
ICP算法在参考点云pi(i为粒子序号)和目标点云qi之间进行最近点搜索,对N个点进行连续的坐标变换,以更接近于目标点云位置。最近点搜索评价指标为所有pi与qi的距离差的平均值f(R,T)[6],即
(1)
式中R、T分别为坐标变化的选择和平移操作。当求解的f(R,T)值满足设定的阈值时,算法停止。
设参考点云P和目标点云Q满足P={pi|pi∈3,i=1,2,…,M},M为参考点个数,Q={qj|qj∈3,j=1,2,…,N},在Q中寻找与pi最近的qj,它们之间的距离d(P,Q)的计算公式为
(2)
对P中所有的点寻找最近点,构成Y=C(P,Q),其中C为映射函数。
为了对参考点云中所有点进行距离评估,引入点云重心,参考点云和目标点云计算公式分别为
(3)
(4)
然后在式(3)、(4)的基础上构建三维点的协方差矩阵ζ[7],即
(5)
设定阈值τ,当fk(R,T)-fk+1(R,T)<τ时,算法迭代停止,其中k为迭代次数。
配准精度评价的一般方法为计算所有点云的距离的均方根误差σ,计算公式为
(6)
2 分层粒子群优化
2.1 PSO算法
采用PSO算法对三维点云的特征点进行提取,将源点云坐标作为粒子群的粒子,将多个点云坐标作为粒子群算法的输入集合,求解所有点云中曲率值较大的点作为点云特征点[10]。设第i个粒子xi=(xi1,xi2,…,xiN)的飞行速度为vi=(vi1,vi2,…,viN),以点的曲率值作为适应度函数,求解第i个粒子适应度极大值pi=(pi1,pi2,…,piN),然后计算所有粒子的适应度极大值pg=(pg1,pg2,…,pgN)。粒子速度更新公式[11]为
(7)
(8)
式中:d为第i个粒子的属性序号;c1、c2为学习因子;ω为上一个时间段的速度权重;r1,r2∈rand(0,1),为速度因子;r∈rand(0,1),为全局速度因子。
2.2 分层PSO算法
为了提高粒子群搜索速率和寻优性能,引入分层PSO算法。分层PSO算法的核心思想是将整个粒子群分成若干子群,根据子群的最优个体和全局最优进行对比[12],从而能够在所有粒子中快速找到最优个体的位置。
首先将粒子按空间分块,对每一块空间中的粒子分别求解最优值,同时根据全局最优值不断调整位置。分层粒子群的空间分割原理如图1所示。

图1 分层粒子群的空间分割原理
按照粒子的初始位置,将粒子群中的160个粒子分为10组,每组均包含16个粒子。在10个子群中分别执行PSO算法进行速度和位置更新,每次更新后都与全局最优解对比,以调整下一次粒子更新方向,这样更容易获得全局最优解,且提高了获取效率。
先将M个粒子群按等额分成L份,建立L个子群,分别在L个子群中采用式(7)、(8)进行迭代,然后将第i(1≤i≤L)个子群的适应度极大值pig与pg对比[13],从而来指导子群粒子的运动方向,分层粒子群结构如图2所示。

pg—全部粒子的适应度极大值;pig—第i个子群的适应度极大值,i=1,2,…,L。图2 分层粒子群结构
子群粒子在进行速度更新时,将子群个体、pig与pg三者结合,共同修正粒子位置,分层粒子群速度更新将在式(7)的基础上进行改进,具体公式[14]为
(9)
式中:c3为全局学习因子;c1、c2和c3值默认设置为2;r3∈rand(0,1),为速度因子。
2.3 分层PSO的三维点云特征提取
将PSO算法用于特征点的提取,选取曲率值大的点作为特征点,采用粒子群快速搜索点云中曲率值大的点,根据数值排序,选择排序靠前的点为特征点。曲率值的阈值决定了入选特征点的数量,然后采用ICP算法来执行特征点配准。具体实现流程如图3所示。

ICP—迭代最近点。图3 分层粒子群优化的三维点云配准流程
3 实例仿真
为了验证分层PSO算法的三维点云数据配准的性能,首先,选择长方形的桌面带纹理的木桌进行可视化点云配准仿真,并计算配准的均方根误差σ和配准时间;其次采用斯坦福点云数据库[15]分别对ICP和分层粒子群优化ICP进行点云配准性能仿真。初始值L=5,ω=1.0。仿真平台为MATLAB 2018。
3.1 分层PSO算法的三维点云配准性能
3.1.1 三维点云配准可视化
图4所示为长方形木桌的源点云和目标点云空间分布,其中红色点为源点云,源点云是经过分层粒子群优化后的特征点云分布;蓝色为目标点云,可以更好地实现源点云配准的可视化对照。从图中可以看出,经过分层PSO后的点云特征提取性能更好,可以反映该木桌的空间结构,并且在所有特征点云中,仅出现1个明显噪声特征点。

图4 长方形木桌的源点云和目标点云空间分布
图5所示为长方形木桌源点云的配准结果。对比图4的蓝色目标点云,本文中提出的配准算法较精确,具体配准性能标准如表1所示。从图5还可以看出,ICP算法对噪声点也进行了配准,表明ICP算法并不能有效去除噪声,因此要使用ICP算法得到点云的精确配准,必须在ICP迭代之前进行有效的噪声消除。
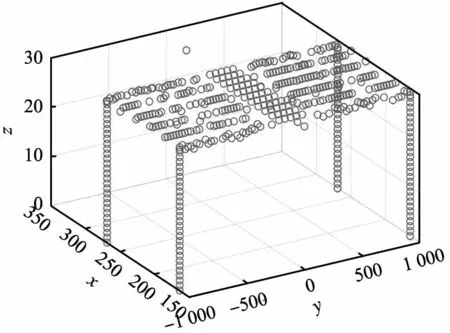
图5 长方形木桌源点云的配准结果

表1 长方形木桌的配准性能标准
3.1.2 分层PSO算法的点云特征优化性能
分层粒子群的子群数L和粒子速度权重ω值影响着PSO算法的收敛速度和全局寻优性能。为了验证L和ω对点云配准的优化性能,差异化选取L和ω,验证本文中提出的算法在点云配准中的性能,仿真结果如表2、3所示。
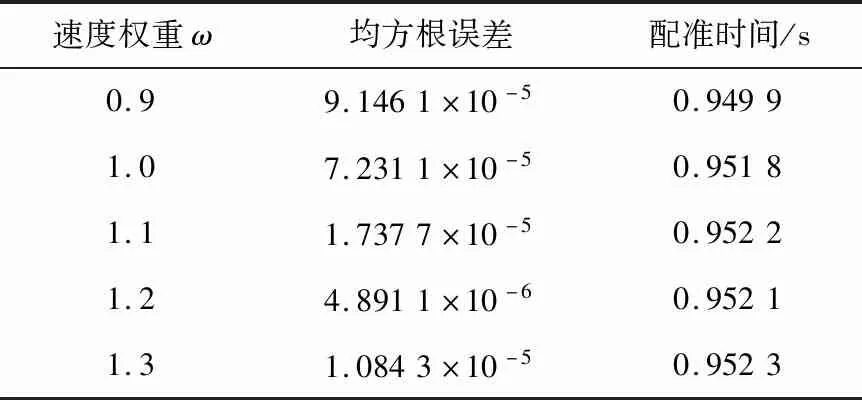
表2 不同速度权重时的点云配准性能
从表2可以看出:ω增大,点云配准的均方根误差呈现先减小后增大的趋势,而配准时间差异并不大;在ω=1.2处,粒子群搜索得到的源点云的特征点经过ICP配准能够获得最优的配准精度。
从表3可以看出:随着子群数的增加,配准均方根误差减小,可见子群数量越多,特征点提取更有效,点云配准的精度更高;当子群数为7时,均方根误差趋于稳定,数值为4.893 3×10-6,但是随着L的增大,配准时间也在逐渐增加,原因是子群数过多引起分层PSO特征点的提取耗时更长。在时间差别不大的情况下,选择子群数为7更适合于该方法的点云配准。
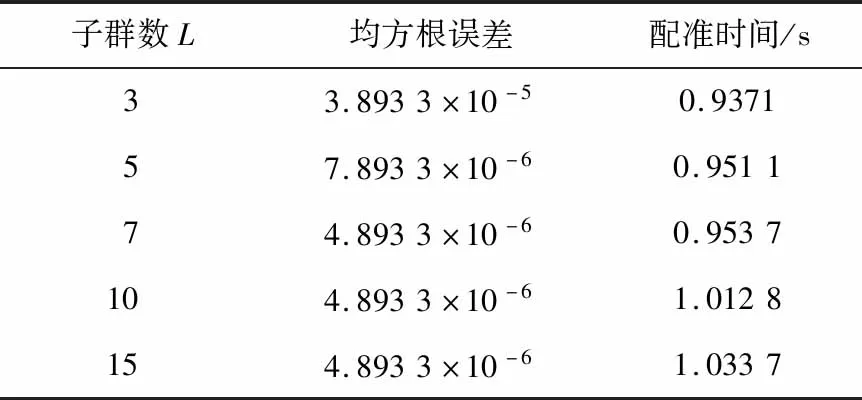
表3 不同子群数时的点云配准性能
3.2 不同算法的点云配准性能
为了进一步验证分层PSO的ICP算法在三维点云配准中的性能,采用常用的斯坦福点云数据样本[15],对标准ICP算法和经过分层PSO优化后的ICP算法分别进行仿真,仿真结果见表4。

表4 不同样本的配准误差
从表中数据可以看出,相比于传统ICP算法,经过分层PSO的ICP算法在斯坦福点云数据库常用的6种不同样本的配准精度略高,但两者差异并不大。该算法在“Blade”样本的配准性能最优,均方根误差仅为4.001 7×10-6,“Dragon”样本配准性能最差,均方根误差为5.160 2×10-6。
6类不同样本在标准ICP和本文中提出的算法的配准时间见表5。在标准ICP中,配准时间主要消耗在ICP迭代过程中,而在分层PSO的ICP算法中,配准时间主要消耗在分层粒子群的点云特征点提取和点云配准2个方面。虽然后者增加了分层粒子群的特征提取时间,但是特征点提取后,减少了ICP迭代的点云数,节省了配准时间。通过与3.1节中长方形木桌配准效率进行对比,当需配准的点数量增加时,配准时间增加,木桌的配准时间为0.951 6 s,而斯坦福点云数据库常用的6种不同样本配准时间均为5~7 s。

表5 不同样本的配准时间
综上,分层PSO的ICP算法在三维点云数据配准中的效率提升明显,但配准准确率优势不大,主要应用环境是大规模点云样本的快速配准,特别适用于大型物体的点云数据匹配。
4 结语
本文中采用分层PSO的ICP算法进行三维点云数据配准,在合理设置粒子速度权重和粒子子群数量的前提下,能有效地提高点云配准效率,并提高配准的精度。通过对不同量级样本的仿真可知,分层PSO的ICP算法配准性能更优。后续研究将对分层粒子群进行差异化调参,进一步提高分层PSO的ICP算法在三维点云配准中的性能。
