基于自适应神经网络智能舵的自动避碰研究
2021-07-06陈汉民李春泽
宁 君,陈汉民,鲁 峰,李春泽
(大连海事大学航海学院,辽宁大连 116026)
随着经济全球化快速发展,世界货物流通日益紧密,据统计,90%以上的货物流通都是靠船舶运输实现的。船舶的日益大型化、不断增大的船舶交通密度、发展迅速的航海技术,以及难以避免的与人为因素相关的海难事故等,都需要船舶避碰的进一步的深入研究,而其中,船舶自动避碰决策就是研究的核心和重点。
目前,已有许多专家、学者对船舶自动避碰进行研究。如LI Wei,et al[1]运用大数据分析法来计算船舶的自动避碰决策,考虑了船舶的3 种会遇情况,建立了3 种评估功能。在此基础上,利用遗传算法求解评估函数,以确定船舶的最佳避碰决策。MOHAMED-SEGHIR,et al[2]在研究避碰时建立了模糊的航行环境,并假设遇到的目标船是均匀且直线运动的。此外,MOHAMED-SEGHIR 使用遗传算法来计算避碰决策。为了准确计算船舶的动态特性,还使用了传递函数和最大角速度。NI Shengke,et al[3]提出了基于船舶操纵性的自动避碰算法。在COLREGs 和航行经验的前提下,采用了改进的遗传算法来提高转向时的避让性能。ZENG Xiaoming,et al[4]结合了ECDIS,使用遗传算法来进行船舶自动避让障碍物的研究,TAM,et al[5]引入避碰因素区域来对遗传算法的输出结果进行控制。李瑶[6]使用遗传算法来进行避碰决策,通过建立船舶领域为依据,来进行路径规划,但是仅仅考虑了单船的避让措施。许兰[7]和顾路平[8]使用了遗传算法去研究船舶的避碰决策路径,在选取避碰的目标函数时,选取以ROC(risk of collision)为依据,综合考虑安全性、经济性来进行避碰路径的研究。王则胜[9]同样基于遗传算法去研究避让决策中的船舶转向幅度,综合考虑我船和目标船的相对运动参数,并将这些参数融合进遗传算法的适应度函数设计中,用适应度值的大小来衡量转向幅度的优劣。
上述研究采用的遗传算法在寻求避碰路径时容易陷入局部最优解,而神经网络算法能很好地解决这一问题。如TANG Huang,et al[10]以AIS 实时收集的信息为基础,提出了一种结合一系列预测方法的神经网络算法去预测船舶的航行轨迹,从而实现船舶避碰。同样基于神经网络算法,XU Qingyang,et al[11]利用一种深层卷积神经网络去学习无人驾驶船的操纵特点并基于视觉系统去实现船舶的操纵避碰。而ZHANG Guoqing,et al[12]重点研究了基于转向点的欠驱动水面船舶路径跟踪控制,其机制是对静态或时变缓慢的障碍物进行避让。此外,为了确保避碰行动的有效性,通过融合神经网络和鲁棒技术,提出了一种鲁棒神经控制。杨宝璋[13]等人利用人工神经网络方法求取碰撞危险度,并将碰撞危险度作为船舶避碰的决策依据,分别采用几何避碰数学模型、矩阵对策和微分对策方法,建立了不同局面下的避碰决策模型。沈海青[14]等人基于深度竞争Q 学习算法和深度多层感知神经网络,提出了一种船舶智能避碰导航方法。而袁宇祺[15]结合了神经网络和遗传算法,在改善BP 神经网络动态指标的基础上,利用遗传算法规划出船舶避碰路径,从而解决了容易陷入局部最小的问题。
本文在考虑COLREGs,航行经验和自动避碰方法的基础上,提出了基于自适应神经网络智能舵的自动避碰算法,该算法可以判断会遇情况,计算碰撞危险度,并自动确定行动时间和行动幅度。基于动态面技术和神经网络方法,该算法还可以解决船舶运动控制系统中由后推法引起的“计算量膨胀”和“维度灾难”问题。通过对“YUKUN”号和“YULONG”号远洋船的Matlab 仿真实验,验证了所提出的自动避碰决策系统的有效性。
1 船舶避碰的过程及相关决策模型
1.1 船舶避碰阶段的划分
船舶的避碰决策流程如图1 所示。
1.2 船舶会遇态势分析
文献[16]将3 种定性的会遇局面进行定量化,以避免避碰行动的不协调性,从而有利于避碰决策的研究。船舶会遇态势划分如图2 所示。
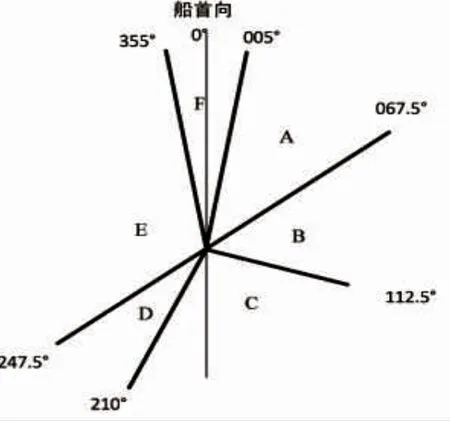
图2 互见中船舶会遇态势划分Fig.2 The division of the situation in the ship meeting
1.3 安全会遇距离
本文基于GOODWIN[17]的船舶领域模型进行船舶避碰决策研究,船舶安全领域区域如图3 所示。

图3 船舶安全领域区域Fig.3 The region of the Ship Safety Domain
1.4 船舶相对运动参数计算
当发现来船时,通过船舶AIS,雷达等设备,获取本船和各目标船的相关运动数据。本船的地理坐标表示为(x,y),目标船的地理坐标表示为(x1,y1),本船船速V0,目标船船速V1,本船的航向C0,目标船航向C1,两船之间的距离用D表示,目标船的相对方位为Tr,也即目标船对于本船的相对方位。船舶相对运动示意图如图4 所示。

图4 船舶相对运动示意图Fig.4 Schematic diagram of relative motion of ships
(1)两船之间的DCPA为

(2)两船之间的TCPA为

1.5 船舶碰撞危险度计算模型
本文在使用自适应模糊神经网络计算船舶的碰撞危险度时,采用DCPA,TCPA的原始数据来进行船舶碰撞危险度的计算。
1.5.1 空间碰撞危险度
其中SCR(space collision risk)以DCPA和船舶安全会遇领域d1、船舶安全通过距离d1的关系来确定。当|DCPA|<d1时认为船舶不能避免碰撞危险,此时,SCR=1;当|DCPA|<d2时,即DCPA大于船舶的安全通过距离,此时船舶没有碰撞危险,SCR=0;当d1≤|DCPA|≤d2时,SCR取值范围随着DCPA的不同而不同。其空间碰撞危险度的隶属函数utt如式(3)所示。

1.5.2 时间碰撞危险度
TCR(time collision risk)是指存在碰撞危险的两船,在时间上的紧迫程度。SCR反映的是距离上的紧迫程度,TCR则反映了时间上的紧迫程度。设船舶从采取避碰操纵时的位置到最晚施舵点处的时间为t1,则当TCPA小于时t1,即认为TCR=1,而海上航行时,船上的雷达等设备一般量程在12 n mile,所以这认为当船舶处于12 n mile 之外时,认为在时间上没有碰撞危险,即紧迫程度为0,时间碰撞危险度反映在TCPA与t1、t2的关系上,TCPA取“+”时,代表他船未驶过最近会遇点,TCPA取“-”时,代表他船已经驶过最近会遇点。于是TCR的隶属度函数utt如式(4)和式(5)所示。
当TCPA>0 时,时间隶属度

当TCPA≤0 时,时间隶属度

DLMA表示船舶的最晚施舵距离。即当船舶驶近到即使本船转向90°时,也不能避免碰撞的距离。DCPADLMA为最晚施舵点处船舶的DCPA值。
1.5.3 船舶碰撞危险度模型的改进
船舶在进行实际的避让操作时,只需要保证SCR或TCR的值减小到安全避让的阈值,即能保证船舶避开他船的措施是有效的。以实例进行说明:当SCR=1,且TCR=0.5 时,只需要采取一定的避让措施使得TCR减小至0,则不管SCR如何变化,即使仍为1,则认为采取该措施后的ROC=0,即不存在碰撞危险。
因此对于SCR、TCR来说,仅需要采取一定的避让措施,确保将其中的最小值降为0,则就可以安全的“避清”他船,且此时的避让措施的幅度较小。鉴于此,则船舶碰撞危险度模型可以做如下的改进:

2 基于自适应神经网络智能舵的自动避碰决策研究
为实现基于自适应神经网络智能舵的自动避碰研究,首先,需要建立一个相对较小的转向变量Δc,然后当航向稳定时自动计算当前的DCPA和TCPA,并比较两船间的DCPA和SDA。当两者数值相差较大时,采用逐渐逼近算法ΔC=ΔC+Δc,直到DCPA和SDA之间的值差小于设定的阈值h¯′,即|DCPA-SDA|<h¯′。h¯′是相对小的正值,ΔC表示转向角度。然后将符合条件的ΔC传递给航向控制单元从而实现转向避让。
2.1 问题描述
船舶航向控制系统非线性数学模型如下[18]:

其中r为船舶艏摇角速度,ψ 为船舶航向,δ 为舵机实际舵角,T为追随性指数,K为旋回性指数,α′,β为Norrbin 系数,d为有界不确定外部扰动,KE是舵机控制增益,TE是舵机时间常数,δE是舵机的命令舵角。
由式(7)可得包含船舶舵机伺服系统特性的非线性航向控制系统数学模型,如下:

x1=ψ,x2=r,x3=δ,g1=1,ϖ2=d,ϖ1=ϖ3=0,u=δE和x=[x1,x2,x3]T∈Rq表示系统状态向量,g2表示控制增益,η2(x)表示未知的非线性函数,u,y∈R分别表示系统的输入和输出。
根据这项研究[19],可以引入以下假设。
假设1:未知控制增益函数gi(·),i=2,3 受限于某一范围,满足:

其中,bmin和bmax分别为某一未知常数的上下界。
假设2:假设|ϖ|是有界的,即存在一个正的未知常数γi和ϖi<γi,i=1,…,n。
假设3:假设系统参考信号yr(t)是t 的光滑、有界的函数,而且yr和导数y˙r,y¨r也有界,即存在一个正值常数B0,使得以下集合成立:

2.2 RBF 神经网络
RBF 神经网络为单隐层神经网络,结构简单,一种典型的局部逼近神经网络,学习收敛速度快,能够逼近任意非线性函数。现以证明它能以任意精度逼近任何连续函数[19],即:h(x)∶Rq→R:

其中x∈Ωx⊂Rq是权向量,并且神经网络节点数l>1。ζi(x)为高斯基函数:
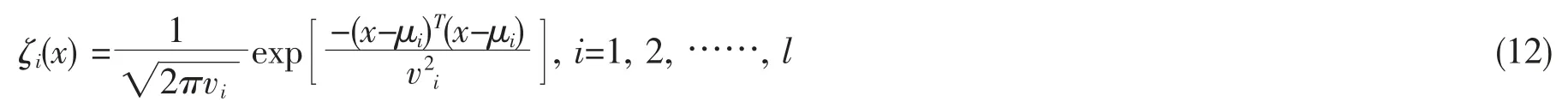
其中vi是高斯基函数的宽度是高斯核函数的中心值。公式(11)中的RBF 神经网络可在∀x∈Ωx⊂Rq的紧集上近似任何连续函数F(x),即[19]


这里引入了一个定理和一个假设[19]。
定理1[19]:通过使用RBF 神经网络和连续函数分离技术,任何给定的连续函数都可以表示为:

假设4:假设所有Z∈ΩZ的ε*>0,并且是逼近误差εi,i=1,2 的未知上界。
2.3 控制设计
步骤一:定义跟踪误差s1=x1-yr,yr=ΔC。由于系统模型中存在未知项,所以无法直接设计系统的控制律,因此使用RBF 神经网络进行逼近:

其中,Δ1=S1(x1)A1yr+ε1+ϖ1。因此,可以得出:

公式(21)中的参数ε*1,yr和ϖ1是有界的,因此||Δ||也有界。通过使用反推技术,可以选择x2的虚拟控制律α2,如下:

通过使用DSC 方法,虚拟控制律α2可以用其估计值z2代替,并且τ2是时间常数:

定义一阶滤波器的输出误差是y2,并且y2=z2-α2,由此得出:

步骤二:参考第一步,定义误差变量s2=x2-z2,则可以表示为:

类似于步骤一,通过使用DSC 方法,虚拟控制律α3可以用其估计值z3代替,并且τ3是时间常数:

定义一阶滤波器的输出误差是y3,y3=z3-α3,可以得出:
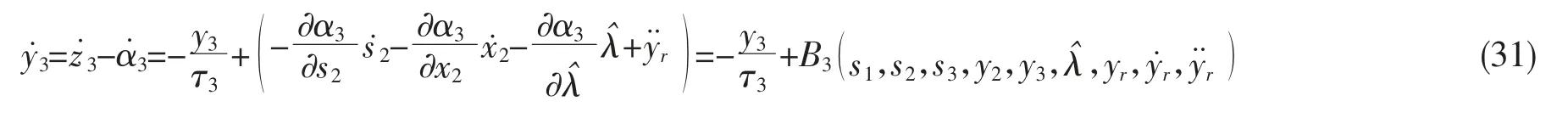
步骤三:参考第一步,定义误差变量s3=x3-z3,则η3(x3)和可以表示为:

通过使用反推技术,可以选择系统控制律u,如下:

的RBF 神经网络自适应律是通过Lyapunov 稳定性准则得出的,如公式(37)所示。自适应权重可以自动调整以逼近动态未知项和干扰,并保证控制系统的动态稳定性。

3 仿真实例
本文基于大连海事大学的两艘远洋训练船YULONG 和YUKUN,进行了Matlab 仿真实验。Norrbin 系数和Nomoto 模型的系数K,T 与船舶的速度和载重有关。考虑到模型的摄动误差和有限的仿真条件,本文将经济航速下的参数值作为仿真的参数输入。
YULONG 的参数如下:
Norrbin 系数β=1,α′=30,K=0.477 7 s-1,T=217.054 1 s-1,LYL=126 m,BYL=20.8 m,dYL=8 m,Cb=0.681 0,Δ=14 278.12 m3,xc=0.25 m,Aδ=18.8 m2.舵的参数:Kr=1,Tr=2.5 s。
YUKUN 的参数:LYK=116 m,BYK=18 m,dYK=5.4 m,Cb=0.559 5,Δ=5735.5 m3,xc=-0.51 m,Aδ=11.8 m2。
船舶自动避碰控制器的初始参数选择如下:k=0.002,k1=0.06,k2=60,k3=1。外界干扰信号选择如下:ϖ=0.001sin(5t).Г=0.2,σ=0.005,τ2=τ3=0.5。权重矢量图的初始值为0。
假设本船是YULONG,目标船是YUKUN。初始条件参数选择如下:x1(t0)=x2(t0)=x3(t0)=0。

表1 两船在交叉相遇时的初始运动参数Tab.1 Initial motion parameters of two ships when they cross each other
仿真结果如图5-11 所示。

图5 DCPA 和TCPA 的时间反应Fig.5 Time response of DCPA and TCPA

图6 空间距离和船首交叉角的时间反应Fig.6 Time response of space distance and bow crossing angle

图7 本船-YULONG 船舶航向的时间反应Fig.7 Own ship-YULONG course time response
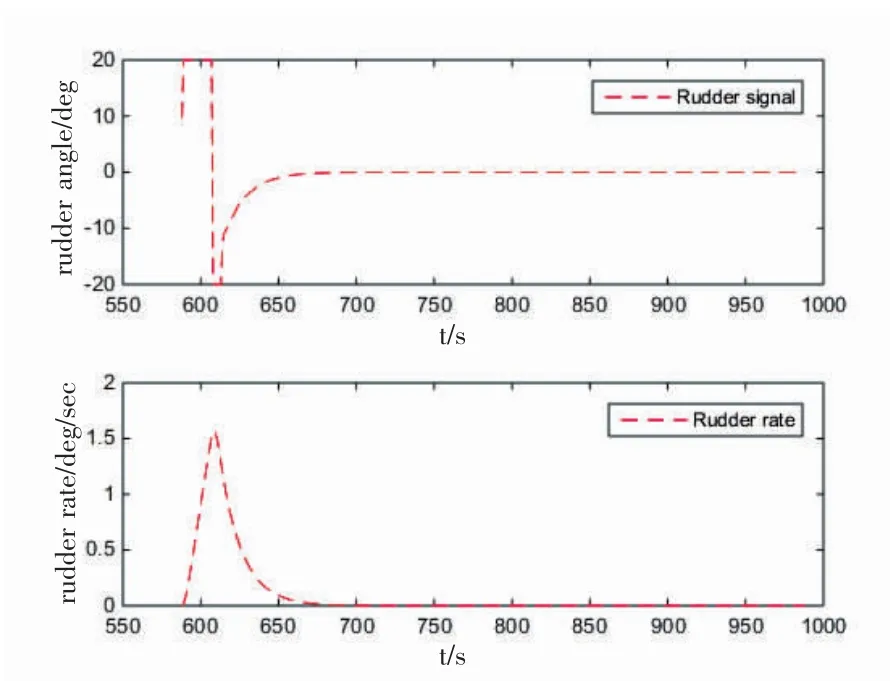
图8 本船-YULONG 舵令的时间反应Fig.8 Own Ship-YULONG rudder time response

图9 本船-YULONG 自适应参数的时间反应Fig.9 Own ship-YULONG time response of adaptive parameters

图10 两船在交叉相遇局面下的绝对运动Fig.10 The absolute movement of the two ships in a crossover situation
根据图5-11 的仿真结果,交叉相遇局面下避碰的全过程如下:
在观察到目标船和获取它的基本信息后,首先,YULONG 确认了本船领域内的SDA 以及两艘船之间的DCPA,TCPA。其次,将SDA 与DCPA 进行比较,判断ROC 是否确实存在。第三,确认会遇局面并确定碰撞责任和避碰行为。在这种局面下,YULONG 是让路船;然后计算ROC 指数。当ROC 指数违反588 s 的设定标准时,应该采取避碰行动。通过使用逐次逼近算法,得出航向改变值ΔC=40°,然后将ΔC=40°传递给优化后的智能舵以采取措施。最后,本船返回原航线。
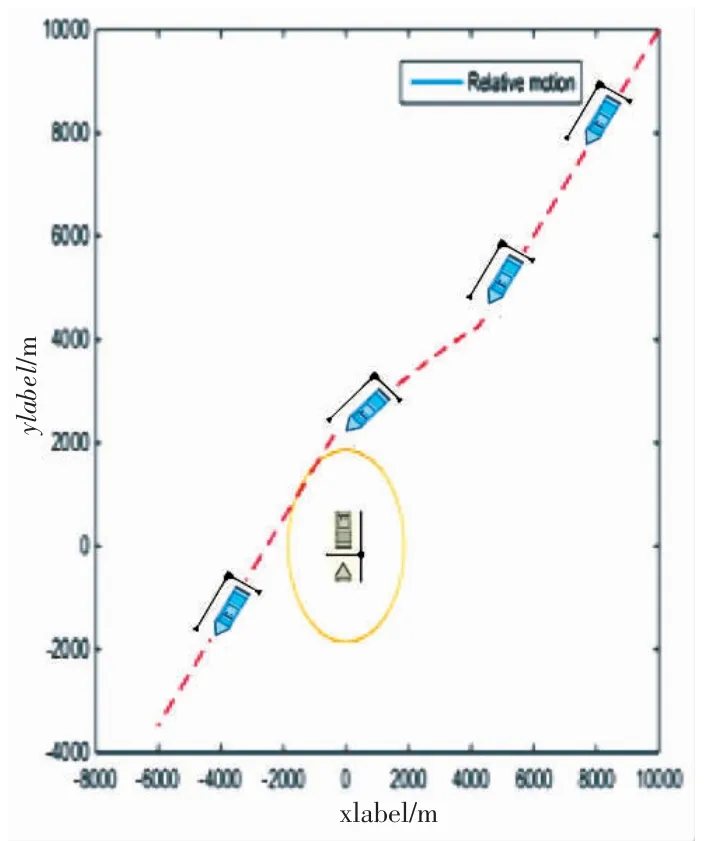
图11 两船在交叉相遇局面下的相对运动Fig.11 Relative movement of two ships in a cross-over encounter
4 结论
本文对船舶自动避碰决策进行了研究,结合COLREGs 和航行经验,并优化了船舶避碰过程中涉及到的数学模型,为船舶自动避碰设计了改进的智能舵。ROC 模型分为SCR 模型和TCR 模型,综合考虑了各种因素对两船会遇局面中所涉及的ROC 的影响,如船舶的相对方位、绝对速度、相对速度等因素。与碰撞几何方法相比,本文提出的算法更加准确且易于工程应用。该算法可以提高会遇局面的安全水平,最大程度地减少碰撞风险,保护海上人员生命安全并进一步帮助值班驾驶员进行船舶避碰。另一方面,它还可以解决船舶运动控制系统中由后推法引起的维度灾难和计算量膨胀的问题,且计算量少。最后,基于两个远洋训练船的Matlab 仿真结果证明了本文所提出的船舶自动避碰算法的性能和有效性。
