基于天牛须搜索自适应的樽海鞘算法
2021-07-06郭明昊祝忠明蒋美琪
杨 兴,郭明昊,方 霞,祝忠明,蒋美琪
(成都理工大学 信息科学与技术学院,四川 成都 610059)
0 引 言
樽海鞘算法(salp swarm algorithm,SSA)[1]是Mirjalili等人基于樽海鞘链在海洋中觅食的种群机制开发的一种群体仿生优化算法。与其他著名的优化算法相比,SSA在许多问题上都证明了它的优越性。但SSA作为一种随机群体优化算法,依旧存在着与其他相似算法[2-3]同样的易陷入局部最优解以及收敛速度慢等缺点。文献[4]提出一种基于反向学习和新的局部搜索算法改进樽海鞘算法用于特征选择和特征的最优子集选择,并验证了算法在大多数使用的数据集中的优越性。文献[5]在樽海鞘算法中引入反向学习与混沌局部搜索, 对测试函数进行全局寻优验证算法的性能。文献[6]在樽海鞘算法中食物源位置引入动态权重因子,构成自适应樽海鞘算法,并与BP神经网络结合形成一种新的预测模型用于对土壤墒情预测。文献[7]将樽海鞘算法运用于TDOA问题,取得了更高的定位精度。文献[8]提出一种具有交叉变换的二进制樽海鞘算法,引入交叉算子增强算法的探索能力,改进的算法在特征选择过程中约90%的数据集优于其他算法。文献[9]提出了混沌樽海鞘算法,使用十个不同的混沌图来提高收敛速度和结果精度,并在特征选择中验证了通过逻辑混沌映射可以显著提高原始SSA的性能。文献[10]提出基于二次积分和火神经模型的混沌樽海鞘算法,将二次积分和火模型产生的混沌振荡引入到SSA算法中。这样可以改善勘探与开发之间的平衡,从而在不同种群之间产生多样性, 跳出局部最优。并在不同的工程应用中验证了改进的樽海鞘算法的可行性。文献[11]提出一种增强型樽海鞘算法,对其进行函数优化验证性能并运用于变速风力发电机中。
为提高樽海鞘算法在求解问题时的优化性能,引入天牛须搜索策略和自适应权重值,提出一种基于天牛须搜索自适应的樽海鞘算法(beetle antennae search and adaptive salp swarm algorithm,BASSA)。主要的改进为:(1)在樽海鞘算法的领导者位置更新中引入洛伦兹函数替代樽海鞘算法中c2随机值,控制领导者的全局搜索范围;(2)引入天牛须搜索机制替代樽海鞘算法的c3的随机值,决定领导者位置更新方向;(3)在追随者位置更新中,为了更好地权衡全局搜索和局部搜索,引入自适应惯性权重,调节自身位置和上一个个体位置对追随者位置更新的权重。通过对多个不同类型的基准函数进行求解优化对比,验证了改进的樽海鞘算法的可行性与鲁棒性。
1 樽海鞘算法
樽海鞘算法起源于樽海鞘链的群聚行为,樽海鞘链群体分为两部分:领导者和追随者。在樽海鞘链中最前端的个体被认为是领导者,其他个体认为是追随者。领导者根据食物源位置引导着追随者移动。将樽海鞘群体对最佳食物源搜索的过程类比为对函数寻优。在樽海鞘算法中,为了更加平衡算法的全局性和鲁棒性,选取一半的种群为领导者。在一个N×d维的空间内搜寻食物源,N为樽海鞘种群数量,d为空间维度,则樽海鞘个体的位置表示为Xn=[Xn1,Xn2,…,Xnd]T,n=1,2,…,N,对应的食物源表示为F=[F1,F2,…,Fd]T,在一个搜索上下界分别为ubd,lbd的搜索空间范围中进行寻优。故在SSA中领导者根据下式进行位置更新:
(1)
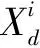
c1=2e-(4t/T)2
(2)
式中,t为当前迭代次数,T为最大迭代次数。
追随者位置更新如下所示:
(3)
2 改进的樽海鞘算法
2.1 领导者的改进
在樽海鞘算法的领导者位置更新公式中c2、c3的随机值分别控制领导者搜索范围和方向。首先引入洛伦兹函数替代c2,提高领导者位置搜索空间的有效性;再引入天牛须搜索算法中的左右须搜索机制替代c3的随机值,决定樽海鞘算法中领导者位置更新方向,使算法中领导者位置前进方向更加有利于对全局最优的搜索。
樽海鞘算法领导者位置更新中,c2是属于均匀分布的随机值,在算法中对其取值具有一定的盲目性,在算法迭代过程中,算法前期为寻找出全局最优解需要算法的个体尽可能地遍历整个搜索空间区域,算法后期,较小的搜索空间能一定程度跳出局部最优解,故该文引入具有缓慢下降速度的洛伦兹函数替代c2值。具体函数如下:
(4)
K=H(t/T;0,1,1)
(5)
式中,A为峰值,x0为位置参数,r为尺度参数,K为通过洛伦兹函数计算出来的参数,t为当前迭代次数,T为最大迭代次数。
天牛须搜索算法(beetle antennae search,BAS)是Jiang等人[12-13]通过对天牛的觅食行为模拟出来的一种仿生算法。天牛觅食的过程通过自身的左右须对食物的浓度感知情况,天牛朝着食物源浓度强的方向移动。天牛须搜索算法中天牛每次迭代后头朝向都是随机的,左右须的位置与两须之间距离和自身的位置有关,具体表示如下:
X(l)=X+d0*dir/2
(6)
X(f)=X-d0*dir/2
(7)
式中,X(l)、X(f)分别表示天牛的左右须,X表示天牛个体自身的位置,dir表示天牛的朝向是随机的。d0为左右须之间的距离,两须之间距离的大小,影响天牛在搜索空间中对最优食物源位置方向的判断,故对两须之间位置根据迭代次数进行衰减。
d0=C*d0
(8)
C为衰减因子,表示为:
C=e-30(t/T)
(9)
在樽海鞘算法中,引入天牛须搜索算法中的左右须搜索寻优方向的策略,得到一种改进的樽海鞘算法(beetle antennae search salp swarm algorithm,BSSA)。将领导者类比为天牛,首先由式(6)、式(7)构建领导者左右须,再通过目标函数计算出领导者左右须位置的适应度值,比较左右须适应度值大小,使领导者在进行位置更新时向具有更佳的适应度值的方向移动。改进的樽海鞘算法领导者位置更新如下:
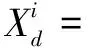
((ubd-lbd)*K+lbd)
(10)
式中,f(X(l))、f(X(f))分别表示通过目标函数所计算出来的左须和右须的适应度值,sign为符号函数,K为通过洛伦兹函数计算出来的参数。
2.2 追随者的改进
该文将自适应惯性权重引入到追随者位置更新中改进樽海鞘算法(adaptive weighted salp swarm algorithm,ASSA)。SSA中追随者的位置更新取决于自身的位置和上一个个体的位置,在上一个个体位置较差或是陷入局部最优解时,追随者盲目的跟随,将会使算法陷入局部最优。文献[14]提出权重值的大小对全局搜索空间寻找最优解和跳出局部最优解均有不同程度的影响。较大的权重值有助于算法在全局搜索空间中找到最优解,而较低的权重值则有助于其跳出局部最优解。故该文在追随者位置更新中引入自适应惯性权重,决定了自身个体和上一个个体对位置更新的影响程度。
追随者位置更新如下所示:
(11)
ω=ωmax*(ωmax-ωmin)*(t-T)/T
(12)
式中,rand为[0,1]上的随机值,ω为惯性权重,ωmax=0.9,ωmin=0.4,自适应惯性权重值主要根据当前迭代次数t与最大迭代次数T决定。追随者位置的改进,进一步提升了算法的局部搜索能力。
2.3 BASSA伪代码
(1)设置BASSA参数:最大迭代次数T,两须距离d0,洛伦兹函数相关参数,种群数量大小N等。
(2)随机初始化BASSA种群,计算每个樽海鞘位置的适应度值,将最佳的适应度值对应的位置作为食物源位置Xbest。
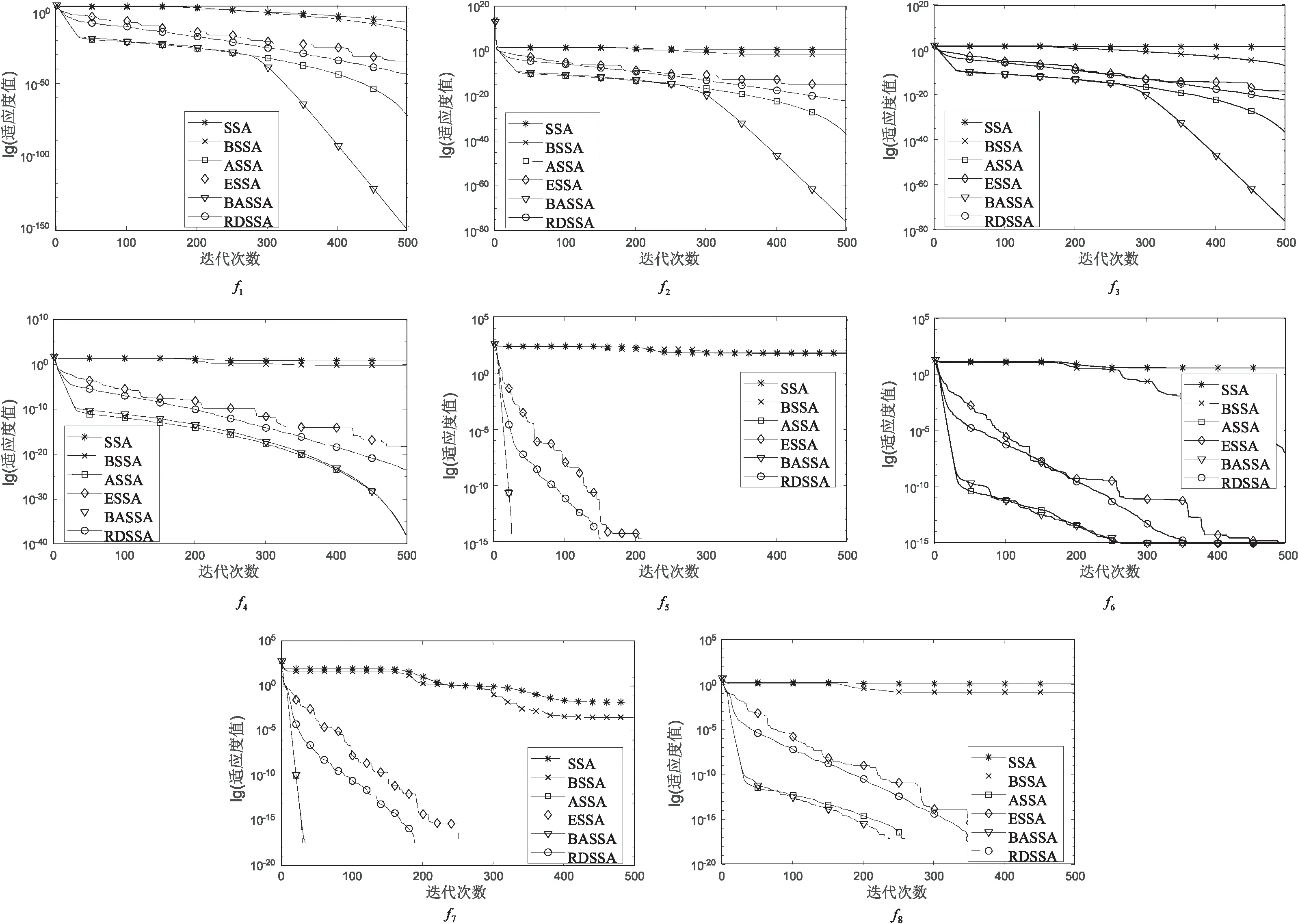
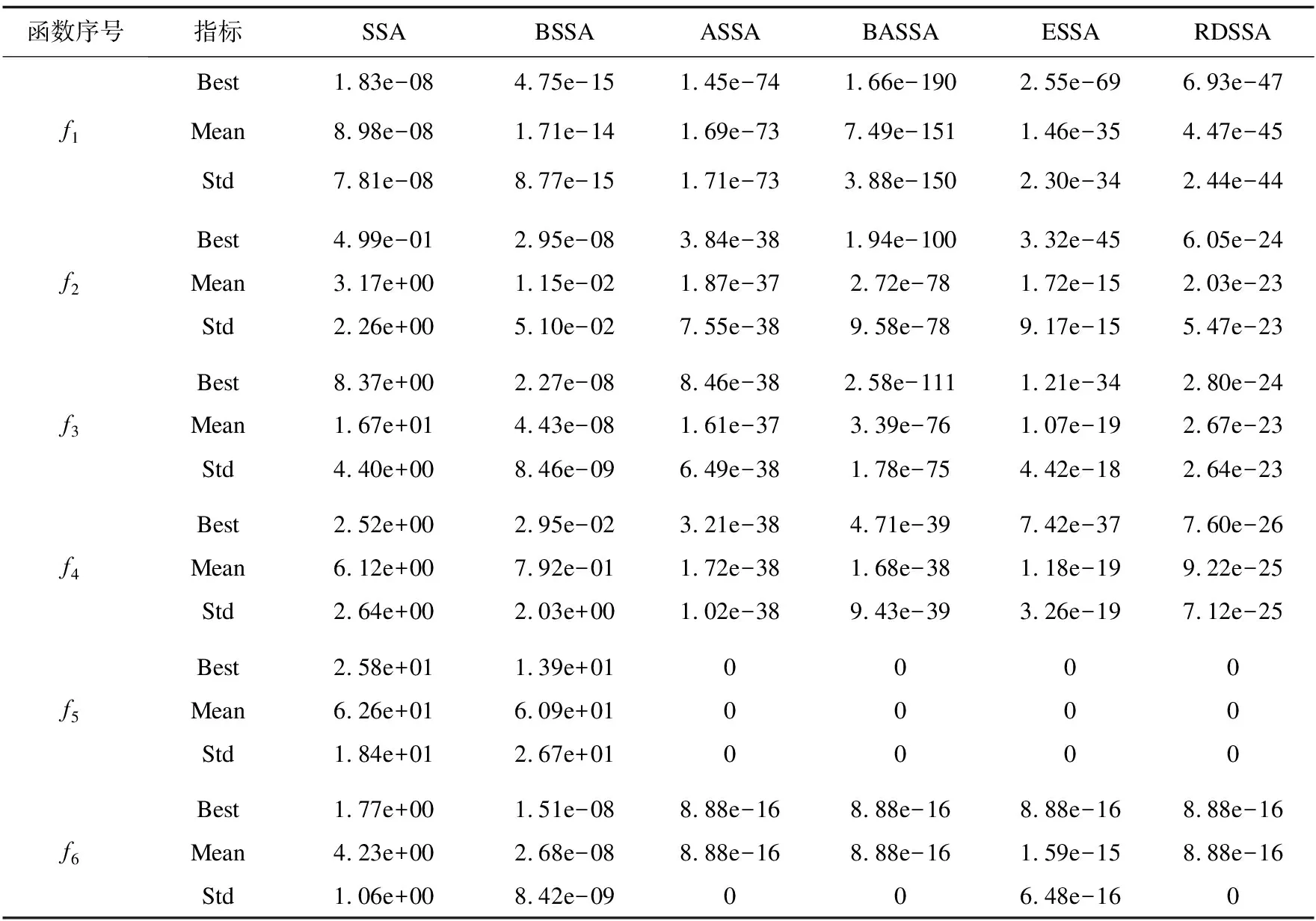
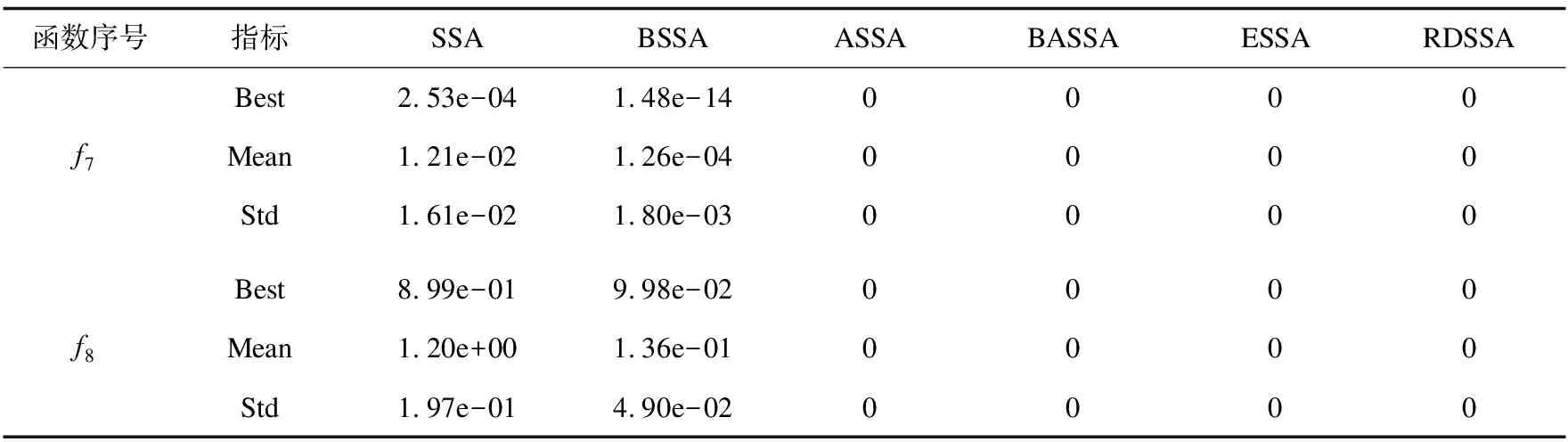
(3)While(t (4)For(i=1:N) (5)if(i (6)根据式(4)、(5)得到洛伦兹函数值。 (7)根据式(6)、(7)计算得到领导者位置的左右须。 (8)根据式(10)更新领导者位置。 (9)else (10)根据式(11)更新追随者位置。 (11)end if (12)end for (13)通过目标函数计算樽海鞘算法位置更新后的种群个体的适应度值。 (14)选取最佳适应度值对应的樽海鞘个体位置与食物源位置进行比较,并更新食物源位置。 (15)t=t+1 (16)end while (17)返回最佳食物源位置Xbest及其适应度值。 SSA在一个N×D维的空间内优化问题的时间复杂度分析如下:在种群初始化设置所产生的时间为θ1,设均匀分布随机值在D维空间中每一维度产生时间为η1,SSA中通过目标函数计算每个个体位置的适应度值的时间为λ1,则求解初始化后所有位置的适应度值所需要的时间为N*λ1。排序得到食物源位置的时间复杂度为η2,故在未进入迭代前所产生的时间为o(ND)。 o(ND) (13) 在追随者位置更新,引入的自适应惯性权重在每次迭代中只运行一次,所需要时间为η2。故BASSA追随者部分时间复杂度为: (14) 综上,改进的BASSA的整体时间复杂度为: T=o(ND)+T1+T2=o(ND) (15) 故改进的BASSA与SSA相比,没有增加时间复杂度。 为验证提出的BASSA的有效性和鲁棒性,在8个包含单峰、多峰、可分、不可分等不同特征的测试函数上对BASSA、BSSA、ASSA、文献[10]的RDSSA、文献[11]中的ESSA以及基本的SSA进行测试。实验设置为在相同的迭代次数下,对比各算法在同一测试函数中的收敛速度和收敛精度。对BASSA算法设置的参数如表1所示,RDSSA、ESSA所需参数根据相关文献中设置相同。测试函数如表2所示。 表1 参数设置 表2 测试函数 本实验在Matlab16b环境下采用M语言进行,同一算法对相同的测试函数独立运行50次,对每次运行结果的最优值进行统计,并计算其平均值和标准差。具体实验结果如表3所示。 3.2.1 与原算法SSA的比较分析 通过图1中各算法对不同的函数优化的收敛曲线可以看出,经过改进的BSSA、ASSA、BASSA与SSA相比,除了在f5函数上,BSSA与SSA基本持平,在其余优化函数上改进的樽海鞘算法在收敛速度和收敛精度上均优于SSA。改进的BSSA与SSA相比,后期的寻优精度上具有明显的优势。改进的ASSA与SSA相比,ASSA在迭代前期能够快速的收敛,并在迭代后期依旧具有较高的收敛速度,且收敛精度明显高于SSA。BASSA综合了BSSA和ASSA的优势后,在收敛速度和收敛精度上,表现出了明显的优势。 经过表3中的BASSA、BSSA、ASSA、SSA在相同的迭代次数下,50次最佳适应度值Best,平均最佳适应度值Mean,最佳适应度值标准差Std的具体实验值表明,在单峰测试函数中改进的BASSA最高达到了E-190级别,其次ASSA、BSSA,相比SSA,寻优效果均具有更加明显的优势。在多峰测试函数中,BASSA和ASSA均能达到理论最优值,而BSSA相比于SSA的寻优精度更高。通过表3中的平均值、标准差值,BASSA、BSSA、ASSA在对相同的函数进行优化时均为最小。表明BASSA具有一定的鲁棒性。 3.2.2 与已改进SSA的比较分析 将该文改进的BASSA与文献[10]的RDSSA和文献[11]中的ESSA进行对比。通过观察图1的收敛曲线,在单峰测试函数中改进的BASSA与ESSA以及RDSSA相比,在迭代前期,具有更快的收敛速度,而在迭代后期,BASSA的收敛速度依旧较快,收敛至一个最优的结果。在多峰测试函数中,BASSA与ESSA、RDSSA均能达到理论最优值,但BASSA达到理论最优值所需迭代次数最少。 图1 各算法平均收敛曲线比较 通过表3相关算法的具体测试结果中,f5、f7、f8三者算法在收敛精度和标准差上相当,在f6上BASSA、RDSSA表现相当且在平均最佳值和标准差上优于ESSA。在其他测试函数上,BASSA均表现为更佳收敛能力和稳定性。 表3 各算法实验测试结果 续表3 该文提出的BASSA在标准的樽海鞘算法的领导者位置引入天牛须搜索机制使樽海鞘领导者向着更优的方向搜索最优解,引入洛伦兹函数控制算法的搜索空间,加快了收敛速度,在追随者位置引入自适应惯性权重改善了算法的局部搜索能力。通过对不同的基准测试函数优化,实验结果表明:改进的BASSA相较于SSA、已经改进的ESSA、RDSSA具有更快的收敛速度,在相同的测试条件下,能够达到更高的收敛精度,并在可行性以及鲁棒性方面都更具有优势。在下一步研究中,尝试将改进的算法应用到具体的工程中。2.4 BASSA算法的时间复杂度分析
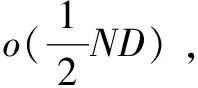
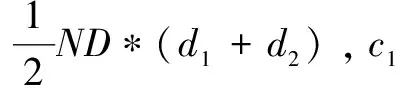
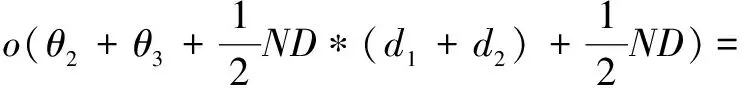
3 算法仿真与分析
3.1 实验设计


3.2 结果分析
4 结束语
