基于卡尔曼滤波和粒子滤波的目标跟踪性能对比①

杨玉林

(同济大学中德学院，上海 201804)

0 引 言

随着智能汽车和智能交通网络系统的逐渐兴起，车辆行驶状态越来越成为国内外相关领域学者的研究焦点，并且取得了很多十分显著的成果[1-3]。由于车辆状态的获取，受到很多因素的制约，如实时性、天气因素、目标遮挡、车辆姿态与尺度变换、相似颜色或轮廓车辆[4]。因此，对车辆行驶轨迹跟踪算法的研究就显得十分重要。

对于线性系统，其状态转移方程是线性的，系统的观测方程是状态变量的线性组合，并且系统噪声和观测噪声符合高斯分布。适用于线性系统的卡尔曼滤波的核心是利用线性递推，来获得当前时刻的最优估计。

对于非线性系统，工程上非线性问题线性化是常见的处理方法，如扩展卡尔曼滤波通过泰勒级数将非线性问题局部线性化，最后利用卡尔曼滤波处理非线性问题[5]。

粒子滤波器是一种也称序列蒙特卡洛采样的近似贝叶斯滤波器，即用事件发生的频率来近似表征事件发生的概率，具体是用N个随机生成的带有不同权重的样本点(即粒子)来近似模拟系统变量的后验概率密度函数[6]。粒子滤波由于不受目标系统是否线性，噪声系统是否高斯分布等限制，广泛应用于各种线性系统和非线性系统，在目标跟踪、自动控制和参数估计等领域取得不错发展。

本文主要是通过建立在仿真环境下的汽车行驶轨迹模型，对比研究卡尔曼滤波和粒子滤波算法在线性高斯系统中的目标跟踪性能。

1 系统数学模型

一般的，系统通常表征为状态空间方程：

系统状态方程：

Xk=f(Xk-1,uk)+εk

(1)

系统观测方程：

Yk=h(Xk)+δk

(2)

其中，Xk是系统在k时刻的状态变量；f是系统的状态转移方程；Yk是系统在时刻k的观测变量；h是系统的观测方程；uk是系统输入；εk系统噪声，其协方差为R；δk为测量噪声，其协方差为Q。

2 两种滤波原理

2.1 卡尔曼滤波

卡尔曼滤波是利用上一个时刻的状态最优估计值来预测当前时刻的状态，并用当前时刻的观测值来修正，以获得当前时刻状态的最优估计值。根据上文的系统数学模型公式(1)和(2)可得一般的卡尔曼滤波公式为：

Xk=AXk-1+Buk+Rk

(3)

Yk=CXk+Qk

(4)

式中，Xk是系统在k时刻的状态变量，A是状态矩阵，uk是k时刻的控制变量值，B是控制矩阵，Yk是k时刻的观测变量，C是观测矩阵，Rk和Qk分别是系统噪声和测量噪声。

卡尔曼滤波在预测阶段用上一时刻的最优估计来预测当前时刻的状态，在更新阶段用当前时刻的观测值来修正在预测阶段的预测值，以此来获得当前时刻的最优估计。其数学表达式如式中表示：

预测阶段：

(5)

(6)

更新阶段：

(8)

(9)

(10)

卡尔曼滤波通过预测和更新两个阶段的迭代来实现目标系统的状态估计，其算法原理如下图1所示

2.2 粒子滤波

粒子滤波器是用N个随机生成的带有不同权重的样本点(即粒子)来近似模拟系统变量的后验概率密度函数[6]。系统变量的后验密度函数需要通过预测和更新两个过程迭代计算，来达到最小方差估计的目的，预测过程是利用系统状态转移方程预测状态的先验概率密度，即通过已经存在的先验知识对未来的状态进行估计。到更新这一阶段，是由当前时刻的测量值，对上一阶段的预测值进行修正，得到目标概率密度函数即系统的后验概率密度。最后根据后验概率密度函数，估算当前状态的期望值。

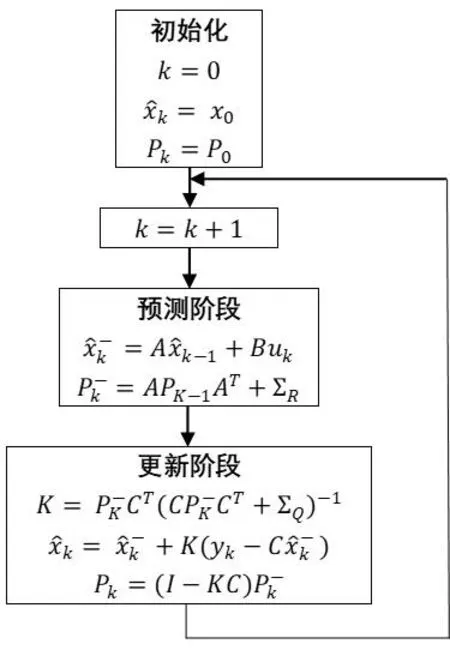
图1 卡尔曼滤波递推过程

2.2.1 预 测

在这一过程中，一般假设系统的状态转移模型服从一阶马尔可夫模型(如图2所示)。每一个状态变量Xk对应一个观测变量Yk，同时每一个状态变量当前时刻的状态Xk只与上一时刻的状态Xk-1有关。

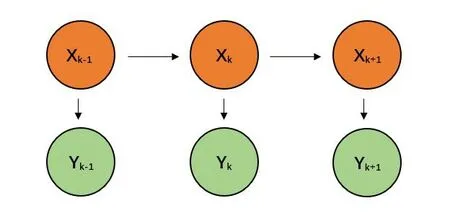
图2 马尔可夫链

预测：已知系统状1：k-1时刻的系统观测值，求解系统在k刻的状态分布，为了进行递推，我们假设在k-1时刻的系统后验概率密度函数为p(Xk-1|Y1:k-1)

计算推导如下：

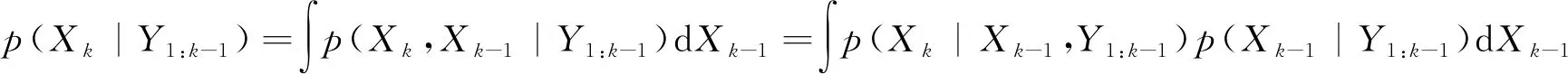
(11)

2.2.2 更 新

在上一步，根据1：k-1时刻的观测值对k时刻的状态值进行预测，得到p(Xk|Y1:k-1)，到更新这一阶段是由k时刻的测量值，对上一阶段的预测值进行修正，得到目标概率密度函数即系统的后验概率密度，推导如下：

(12)

其中归一化常数：

(13)

粒子迭代过程：

图3 粒子迭代过程

2.2.3 序贯重要性采样

2.2.4 重采样

粒子滤波算法中不可避免的存在粒子退化现象[7]，即经过多此迭代计算后，少数几个有效的粒子权重很大，而大多数的粒子权重很小，甚至随着迭代次数的增加，一个或几个粒子的权重占整个粒子群的大部分权重，而其他粒子的权重基本为零的现象。为解决这个问题，通常采取的方法是重采样，即在每一次的迭代过程中，多采集那些占据整个粒子群权重比较大的粒子，对那些权重比较小的粒子少采集甚至不采集。重采样的方法有很多，比较典型的有随机重采样、残差重采样和多项式重采样等[8]。

2.2.5 估计输出

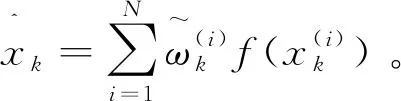
3 系统建模和仿真结果分析

3.1系统建模

为了建立汽车行驶轨迹跟踪模型，(如图4所示)

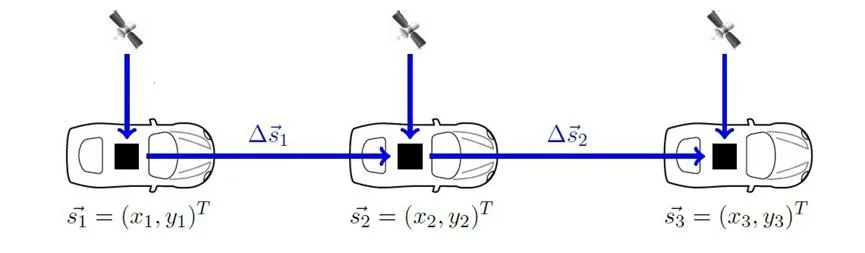
图4 汽车仿真场景

汽车的状态向量可以表示为：

(14)

从时刻k-1到时刻k的汽车运动状态，可表示

(15)

汽车状态的观测向量：

(16)

因此，汽车的状态转移矩阵为方程：

(17)

汽车的观测方程为：

(18)

其中矩阵A，B，C为二阶单位矩阵；εk为系统噪声，其均值为0，协方差矩阵为R；δk为测量噪声，其均值为0，协方差矩阵为Q。

3.2 仿真结果

为了能够定性地和定量地对比显示出卡尔曼滤波和粒子滤波在线性高斯系统的目标跟踪性能的差异性，绘制了卡尔曼滤波和粒子滤波的估计结果与真实值的误差折线图，如图5所示。可以看出，卡尔曼滤波在线性高斯系统中表现出更好的性能，其估计的误差均值和方差明显优于粒子滤波。在MATLAB软件环境下仿真结果如下：

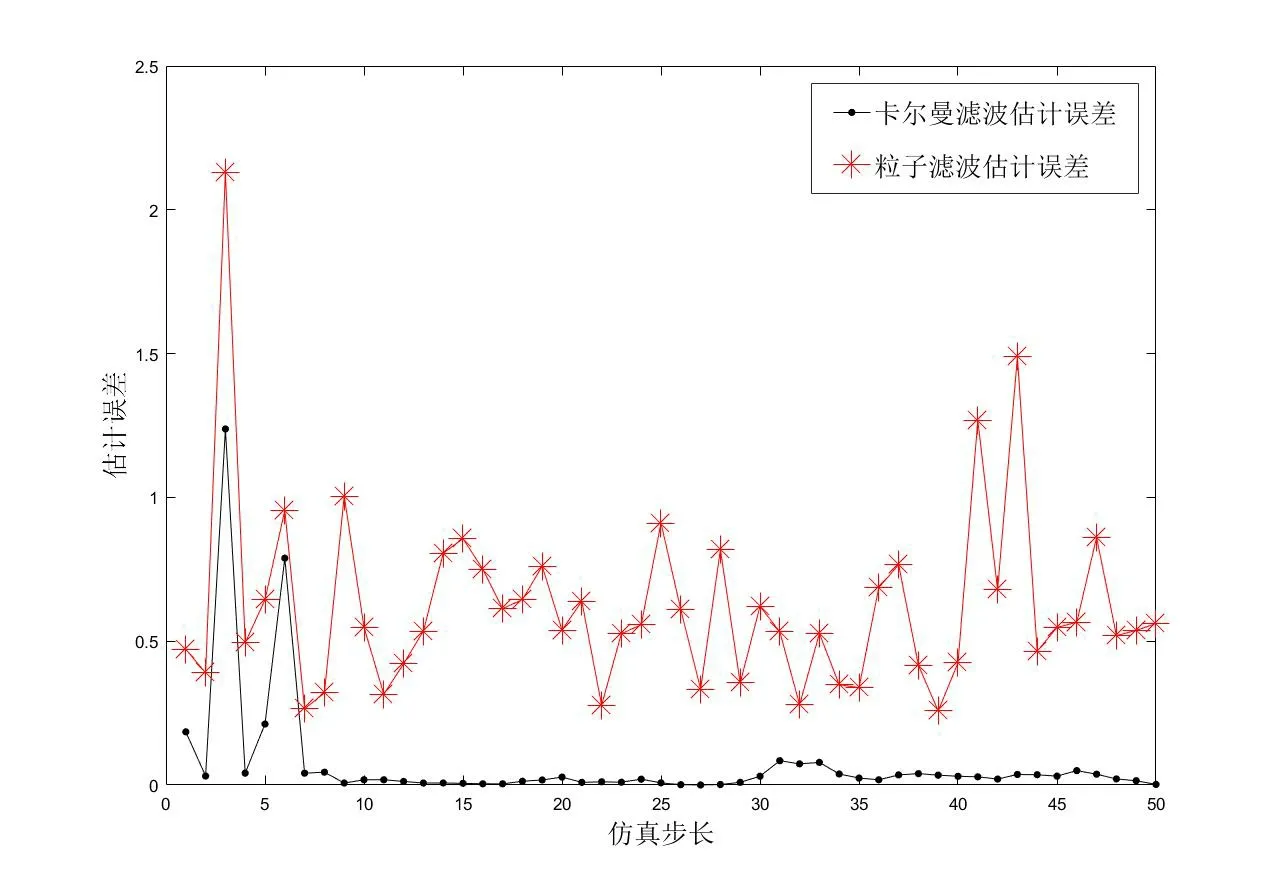
图5 滤波估计结果误差

4 结 语

首先通过公式推导和算法程序框图，介绍了卡尔曼滤波和粒子滤波算法的原理和步骤。在设定的仿真条件下，建立目标系统的状态转移方程和观测方程，利用卡尔曼滤波和粒子滤波在MATLAB 中进行建模：通过对比两种滤波器的估计误差，表明了卡尔曼滤波在线性高斯系统中的优势，粒子滤波估计误差整体较小但在粒子迭代，重要性采样函数，粒子退化，重采样等步骤上具有更高的算法复杂度。