钢管内置刚性节点承载力与实用计算方法研究①
2021-07-05李飞涛魏新江曹庆帅
李飞涛,邢 丽,魏新江,张 茹,黄 超,曹庆帅,金 海
(1.安徽理工大学土木建筑学院,安徽 淮南 232001;2. 浙大城市学院土木工程系,浙江 杭州 310015;3. 浙江省工业设计研究院,浙江 杭州 310052)
0 引 言
钢管由于具有截面封闭、受力性能优异、轻巧美观、经济效益好等优点,广泛用于海洋平台、工业厂房、房屋建筑等建设中[1-2]。目前钢管之间的拼接方式主要分成现场直接焊接[3-5]和螺栓连接。现场焊接连接对工人技术要求高,而且部分钢管由于管径较大,需要仰焊,焊缝质量难以得到有效的保证。螺栓连接中,法兰连接[4-7]和螺栓拼接连接[4-5,8]更易满足预制装配施工工艺的需要,且能获得更好的受力性能,但在外观上形成明显的法兰盘和连接件,破坏了钢管的流线美,实际工程应用上受到了限制。因此,尚需进一步研究更为便捷、高效、美观的钢管拼接构造技术。董石麟等[9]和邢丽[10]分析了“水立方”结构矩形钢管、方钢管的焊接空心球节点的力学性能,并提出实用计算公式,丰富了空间结构刚性节点的设计理论。Blachowski B等[11]针对某电信塔的法兰连接节点进行了非线性有限元分析,该节点由两个法兰焊接到钢管上,再用预紧螺栓连接固定。Simões R等[12]提出了一种隐蔽螺栓拼接节点形式,钢管在接头部位焊接一同直径开孔钢管,内设内衬管,然后利用螺栓使之与开孔钢管连接。刘康等[8]提出了方钢管柱内套筒单向螺栓柱-柱拼接和对穿螺栓柱-柱拼接两种节点构造形式,拼接件采用内套筒,紧固件采用高强螺栓、单向螺栓和对穿螺栓。课题组前期提出了一种钢管内置刚性节点[13-14],并进行了相关试验研究[14-15]。在此基础上,建立了精细化有限元模型,进行了参数分析,结合理论研究,最后推导出轴力作用下新型钢管内置刚性节点的实用计算公式。
1 节点构造及试验
钢管内置刚性连接方式见图1,其中焊接的部分在工厂制作,到了现场再用螺栓连接,操作简单,施工速度快,便于工厂标准化制作,从而保证节点质量,既规避了现场焊接,又弥补了现有螺栓连接的不足之处,由于节点在钢管内,保证了钢管自身的流线美,因此具有一定的工程应用性。
详细的试验结果参见文献[14, 15]。限于篇幅,仅以试件SJ-3和SJ-5为例,并将在第3部分与有限元结果进行分析比较。
2 有限元模型
通过有限元软件ANSYS展开分析,几何模型见图1。考虑到节点位置的复杂性,内插钢板与钢管采用直接固结连接,螺杆简化为圆柱体形状模拟,其直径与螺栓公称直径相同。
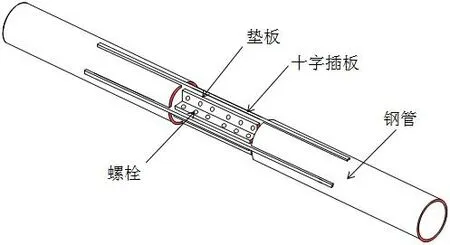
图1 钢管内置刚性连接
钢管、十字插板、垫板选用20节点的Solid95单元,螺栓选用Solid92单元。由于模型形状不规则,网格划分中,首先利用工作平面切割法,将模型切割成多个规则的块体与少量不规则的块体。调整网格划分控制参数,受力复杂部位及重点研究部位的单元网格局部细化,划分较为密集,次要部位的单元网格划分较稀疏,这样即可以提升计算效率,也能保证计算精度。
在模型中,垫板与十字插板,以及二者与螺帽之间、螺杆与孔壁之间需要考虑接触分析,在ANSYS中通过定义目标面和接触面来实现,为了避免矩阵的奇异,模型中各个接触面的网格尺寸划分时应保持接近。建立的接触对有螺杆与孔壁之间,插板与垫板之间,目标面采用Target 170单元定义,接触面采用Contact 174单元定义,设置各个接触面之间的初始几何间隙为零,接触类型为库伦摩擦,摩擦系数取0.3[16-18]。
建模时试件材料本构模型根据实测应力—应变关系[14]简化为三线段模型(如图2(a)所示),模型中屈服强度、抗拉强度均采用实测平均值。螺栓为10.9级,屈服准则采用三直线线性模型,见图2(b),屈服强度990 MPa,抗拉强度1160 MPa,弹性模量200 GPa,泊松比0.3。
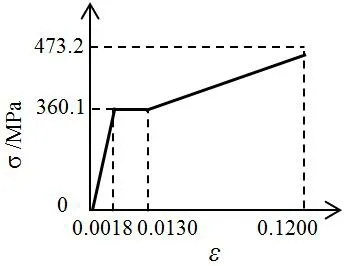
(a) 钢材 高强螺栓
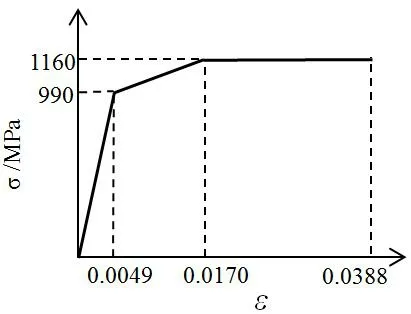
b) 高强螺栓
3 试验与有限元结果对比分析
比较分析试验与有限元结果。图3给出了荷载—位移曲线,横轴为节点竖向位移,纵轴为竖向荷载值。其中图3(a)为压力作用下试件SJ-3的曲线,可以看出:在加载开始阶段,位移随荷载的增大基本呈线性增长,然后变为非线性增长,这时试件出现整体弯曲变形现象,到了后期,位移保持快速增加,达到破坏荷载后,开始快速卸载。图3(b)为拉力作用下试件SJ-5的曲线,在加载开始阶段,位移随荷载的增大基本呈线性增长,然后变成典型的非线性增长,这时试件进入了塑性阶段。当十字插板内插长度足够长时,节点发生钢管拉断破坏,在破坏前经历一个非常长的变形发展阶段后,节点发生典型的延性破坏;当十字插板较短时,节点发生十字插板和钢管之间的剪切破坏,为脆性破坏模式。由试件von Mises应力分布图(图4)可知,由于剪力滞后影响[19-20],钢管截面应力分布不均匀,在钢管和十字插板连接部位应力集中严重。

(a) SJ-3

(b) SJ-5
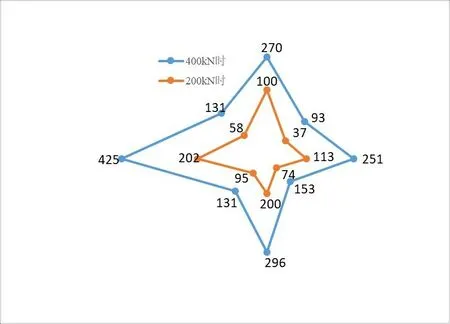
图4 钢管截面实测von Mises应力分布图(MPa)
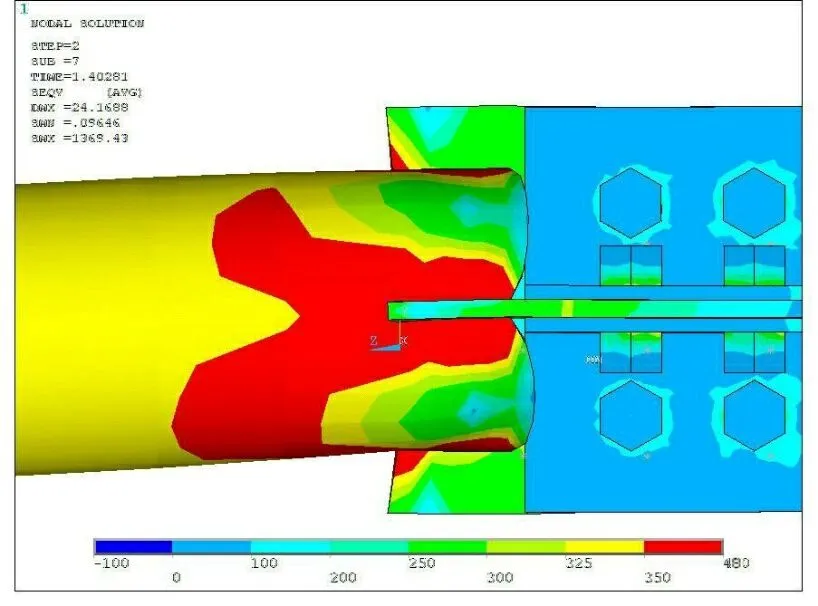
(a) 有限元分析结果

(b)试验结果

表1 试验结果与有限元分析对比
试验结果汇总见表1所示。结合图3可知,有限元所得与之吻合良好。但对于试件SJ-3,在由弹性向塑性的转变阶段中存在较大偏差, 这可能是由于通过简单拉伸试验获取的本构关系和实际试件存在偏差所引起。破坏荷载对比结果基本相同,试验值略大。主要原因是试验试件的钢管和十字插板通过焊接连接,而有限元模拟中直接采用固结连接。此外,材料特性在试件加工时可能会受到影响,试验设备以及测量也有些许误差。
图5、图6、图7分别对比列出了不同条件下的有限元分析得到的变形形状与试验破坏形状比较,即压力作用下钢管屈曲破坏、钢管正截面拉断破坏、钢管与十字插板焊缝剪切破坏三种不同条件。为了更清楚地显示结果,此处有限元分析结果放大4倍显示。可以看出,该模型较好地模拟了新节点在拉压作用下的力学行为与破坏性状。

(a)有限元分析结果

(b)试验结果

(a)有限元分析结果

(b)试验结果
4 节点参数分析
4.1 影响承载力及破坏特性的参数分析
钢管与十字插板间焊缝长度与钢管外径比(lw/D)、十字插板截面与钢管全截面面积比(Ac/A)、垫板截面与钢管全截面面积比(Ad/A)是影响内置刚性连接节点承载力和破坏模式的主要因素[9-10]。参考现有研究基础,研究了三种管径的24组节点模型,其参数变化范围分别为:0.5≤lw/D≤1.0,0.8≤Ac/A≤1.3,0.8≤Ad/A≤1.2。
4.2 钢管与十字插板间焊缝长度与钢管外径比
为了研究钢管与十字插板间的焊缝长度与钢管外径比(lw/D)对试件产生的影响,对24组节点在拉压分别作用下进行了分析,并参考美国规范AISC[18]、加拿大规范CSA[21]、欧洲规范Eurocode[22],引入截面效率系数U,以表示有限元分析得到构件受拉(或受压)承载力与构件全截面受拉(或受压)理论承载力之比。结果如图8所示,其中纵坐标为U,横坐标为lw/D。从图中可以看出:lw/D的临界值为0.65;当lw/D<0.65时,随着lw/D的增加,节点承载力增加;当lw/D≥0.65时,随着lw/D的增加,节点承载力不再增加。

(a) 拉力作用
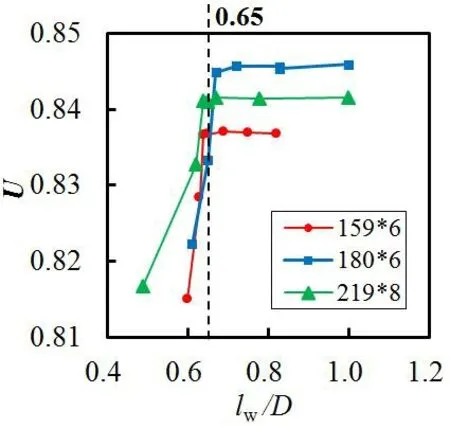
(b)压力作用
有限元分析还表明:当lw/D<0.65时,拉力作用下钢管表现为剪力滞后导致的剪切破坏,压力作用下钢管表现为净截面屈曲破坏;当lw/D≥0.65时,拉力作用下槽末端钢管表现为全截面强度破坏,压力作用下试件表现为全截面在连接区域外围局部屈曲。
4.3 十字插板横截面与钢管全截面面积比
确保钢管、螺栓、垫板不早于插板失效,改变插板横截面与钢管全截面面积的比值Ac/A,对三种型号的试件展开模拟。结果见图9,其中纵坐标为U,横坐标为十字插板的横截面与钢管全截面的面积比Ac/A。可以看出:Ac/A的临界值是1.04;当Ac/A<1.04时承载力显著降低,十字插板破坏;当Ac/A≥1.04时,承载力变化不大,槽末端钢管表现为全截面强度破坏。

(a)拉力作用

(b)压力作用
4.4垫板横截面与钢管全截面面积比
确保钢管、螺栓、十字插板不早于垫板失效,以垫板横截面与钢管全截面面积比Ad/A为变量,展开有限元模拟,得到面积比Ad/A的临界值,以及对截面效率系数U的影响,如图10所示,可以得出:Ad/A的临界值为1.04;当Ad/A<1.04时,表现为垫板破坏,随着Ad/A减小,承载力显著降低;当Ad/A≥1.04时,表现为钢管全截面强度破坏,承载性能变化不大。

(a)拉力作用
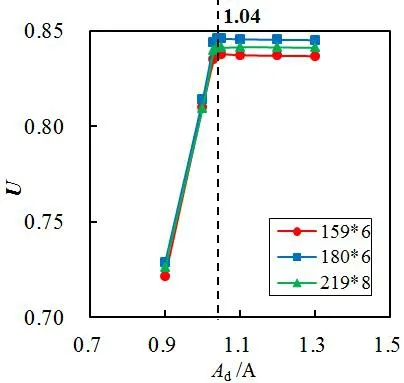
(b)压力作用
5 理论解及实用计算公式
5.1 理论解


(a截面塑性发展

(b)全截面塑性
引入无量纲参数ξ,并表示为
(1)
塑性发展过程中,施加在试件上的轴力N与冲切面上应力的关系可通过下式计算得出:
T=2πkftDmeanξ
(2)

当塑性区发展到钢管全截面时,ξ从0→1, 此时轴力达到最大值,即
T=2πkftDmean
(3)
式(3)即为节点承载力计算公式,在此基础上,结合前面的试验以及有限元计算,可得到实用的计算方法。
根据AISC[18],CSA[21]和Eurocode[22]规范,节点承载力计算公式建议为以下形式:
(4)
An=πtDmean
(5)
其中,0.9为力分项系数1.11的倒数,U为钢管截面效率系数。
5.2 实用计算公式
将有限元计算得出的节点承载力通过πtDmeanf无量纲化后作为纵坐标,以lw/D为横坐标,见图8所示,给出钢管截面效率系数U的实用计算公式如下:
当lw/D>0.65时,U= 1.0
(6)
当0.5≤lw/D≤0.65时,U=0.35+0.85lw/D
(7)
表2所示为4个钢管发生强度破坏的破坏荷载与上述建议公式的计算结果进行比较,得出公式的安全储备约为1.4~2.0。

表2 建议设计公式检验
对于轴力作用下的新型钢管内置刚性节点,可以如下设计:
(1)根据焊缝承载力要求确定钢管与十字插板的拼接长度lw,
(8)
同时,lw必须满足构造要求,即max(40mm,8hf)≤lw≤60hf。
(2)计算lw/D,并按照公式(6)和(7)进行计算钢管截面效率系数U。
(3)强度计算公式为:
NR=0.9UAnf
(9)
式中:An按式(5)计算。
(4)对于受压构件还需要验算稳定:
(10)
式中:φ为构件的稳定系数。设计时,在构造上要满足:十字插板截面积要大于钢管截面积1.14倍,垫板截面积大于钢管截面积1.05倍,十字插板和钢管采用U形围焊。
6 结 论
(1)试验已研究了轴力作用下新型钢管内置刚性节点的力学行为,建立了ANSYS精细化模型,进行了参数分析,二者结果对比吻合良好。
(2)得到了轴力作用下影响其节点承载力的三大因素,这些因素包括钢管与十字插板的焊缝长度与钢管外径比、十字插板截面与钢管全截面面积比、垫板截面与钢管全截面面积比。
(3)分析表明,轴力作用下的内置刚性节点存在剪力滞后效应,在十字插板与钢管连接处应力集中严重,节点设计时应考虑剪力滞后效应影响。
(4)结合试验、有限元和理论研究,建立了轴力作用下圆钢管内置刚性节点的实用计算公式,丰富了钢管结构节点设计理论,可以为实际工程设计提供参考。
