具有自动回溯的机动目标航迹精细化分段识别

乔殿峰，梁彦,*，张会霞，赵鹏蛟

1. 西北工业大学 自动化学院 信息融合技术教育部重点实验室，西安 710129 2.北方自动控制技术研究所，太原 030006

目标机动是常见的运动形式，机动目标跟踪在军事与民用领域都有着广泛的应用，如空天预警、拦截制导、交通管制等。由于跟踪过程中目标的运动模型具有不确定性和航迹位置数据带有噪声，基于模型的轨迹跟踪[1]的方法会导致航迹分段精确较低的问题。因此，数据驱动的轨迹跟踪算法越来越受到重视[2-4]，能够进一步从轨迹数据中提取出语义信息，为指挥员提供辅助决策提供支撑[5-7]。

轨迹的精确分段需要准确地估计目标运动模式和目标状态。现有航迹分段方法可看作模式识别中用于参数化复杂曲线的方法[8-9]，能够在不给出运动模型的情况下，进行航迹分段。在此基础上，Linder和Schell提出了在曲线拟合中加入连续性约束指标的分段航迹识别器(Segmenting Tracking Identifier, STI)[10]，它是能够跟踪机动目标的非贝叶斯方法，将目标轨迹动态划分为一系列轨迹段。首先，检测模式发生转换的时刻，STI对航迹进行分段，然后在最小二乘意义上确定每段目标运动的最优模型参数。但是该算法中仅考虑了位置连续性和航向角连续性指标，未考虑速度连续性指标，也没有对多连续性指标标准化，造成分段策略时间代价太大。为此，在拟合代价函数中加入速度连续性指标，改善了对航迹时间相关性信息的利用，提高了分段精度、减少了分段消耗时间[11]，但是它的时间消耗和分段精度仍然难以满足要求。

鉴于恒速(Constant Velocity, CV)和协同转弯(Coordinated Turn, CT)是机动目标最常见的运动模式，真实航迹都可以通过这两种模式的组合来描述[12-13]。CV和CT的区别在于转弯角速度的大小，转弯角速度为零时，即为CV运动，反之，则为CT运动。因此，可以通过判断转弯角速度来得到机动模式，在运动模型的滤波框架下使用角速度估计的方法能够更好地进行目标跟踪[14-15]，为机动目标航迹分段提供新的思路。由于机动目标通常都会执行协同转弯等运动模式，目标的机动模型切换检测也是航迹分段的重点研究方向[16]。Lee等提出了基于最小描述长度(Minimum Description Length, MDL)的轨迹分段算法[17]，将航迹分段问题转化为求解MDL最小代价问题，实现对分段的准确性和高效性的权衡。基于移动对象数据库中(子)轨迹的代表性的轨迹分段和采样方法可以自动估计分段的数量和分段边界，从而识别有关其代表性的同质分段[18]。但是这些算法都是对带有小噪声的低速轨迹数据进行离线处理，且无论是MDL准则还是异常容忍准则和标准差准则都仅仅考虑了数据长度的问题，并没有考虑目标运动模型切换和航迹位置数据存在噪声的问题，因此，在很多情况下，分段精度较差。

目标机动通常建模为混合系统，其中连续空间取值的状态演化由马尔科夫过程表征，运动模式切换由马尔科夫链表征。采用经典的交互式多模型(Interacting Multiple Model，IMM)估计方案，首先估计位置速度，进而构造出转弯角速度的初步估计，并用于角速度的精细化估计[19-20]。Arasaratnam和Haykin在IMM框架下提出了自适应转弯角速度估计算法[21]，也能够准确地估算出角速度。目标运动过程中，角速度的变化是由于模式切换引起的，虽然IMM算法能够根据模式切换时刻来判断分段点，不过对于模式变化小的轨迹，存在分段点缺失的问题。综上所述，现有的航迹分段研究没有有效解决机动目标运动模型切换下航迹准确分段问题，也难以满足日益增长的机动目标航迹精确分段的需求。

本文提出了双层精细化航迹分段框架，预分段层利用基于IMM算法检测目标运动过程中的模式切换，完成航迹预分段，得到目标模式变化明显区域的预分段点；再分段层利用改进的STI算法对模型差异小的非预分段区航迹进行回溯迭代优化再分段，得到更为精细的分段点。该框架实现了对于机动目标航迹的精细化分段识别。

1 问题描述

空中目标类型多种多样，每种目标类型运动样式千差万别，通过分析和挖掘目标的运动模式及运动轨迹，进一步为目标识别及意图判断提供支撑。在场景构建时，必须对目标运动模式进行确定，以确保它们涵盖所有可能的机动情况[10,22]。通常可用CV/CT运动模型曲线簇来表征大多数机动目标的运动。然而，按照现有多模型方法设置多个同类型模型跟踪，模型概率的变化趋势不明显，难以发现预分段点。而且，由于多模型估计方法得到的模型概率切换存在延迟；此外，航迹位置数据带有噪声，模型概率可能发生局部异常情况。上述情况均导致航迹分段不精确。

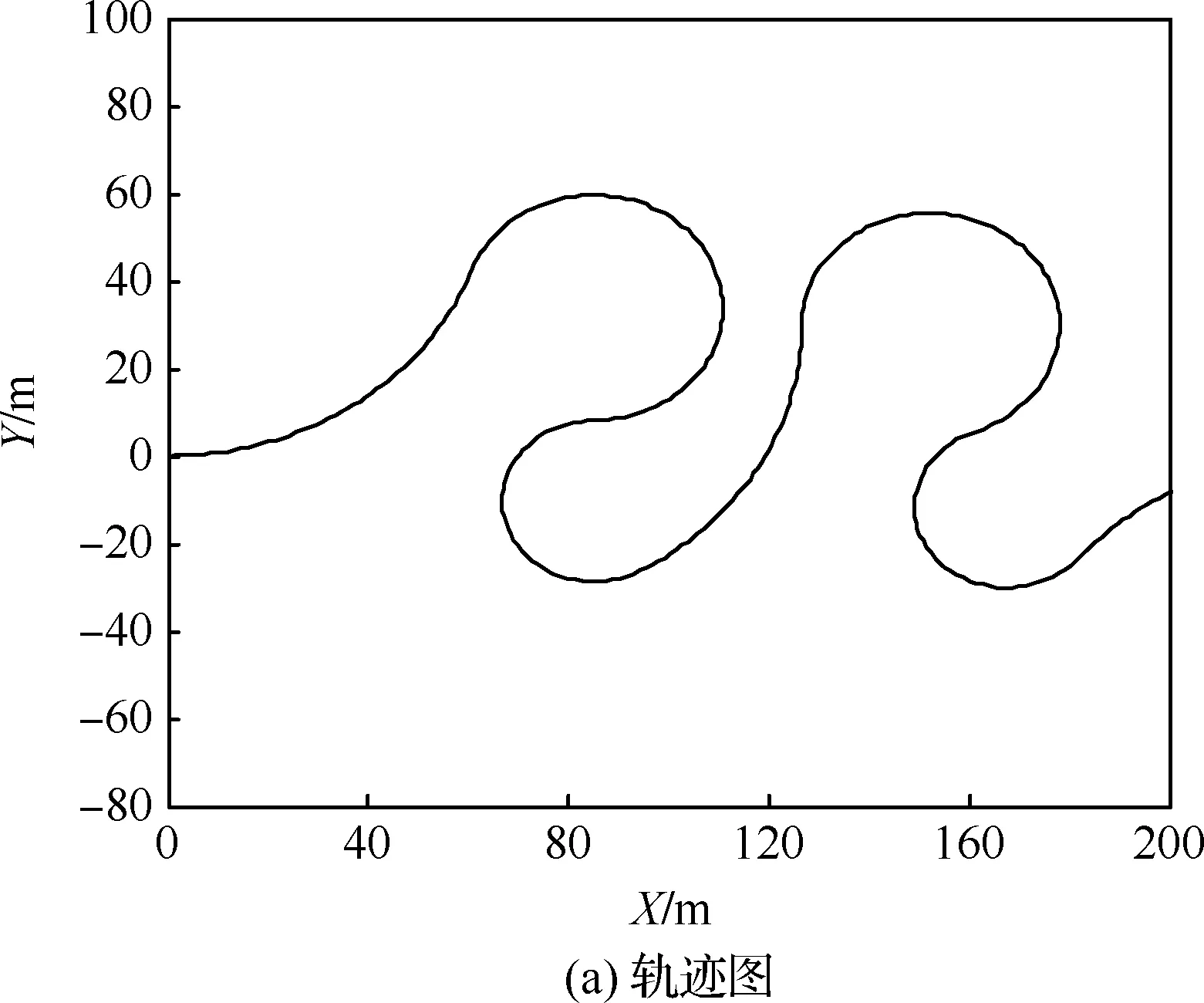
在目标运动模式未知情况下，直接在轨迹数据上做跟踪，找到模式的切换点，即航迹的分段点，以便对航迹做事后分析，进而总结出航迹的语义信息，来进行目标运动的异常检测或航迹预报，数据驱动的航迹分段算法能够解决运动先验模型集设计困难和分段点存在延迟且受噪声影响的问题。考虑机动目标航迹数据为带观测噪声的二维位置量测序列。改进的STI算法[11]解决了STI算法仅考虑目标位置与航向角连续性、特征量不完备、STI连续性指标权重先验给定、以及缺乏设计准则的问题，引入了速度连续性指标，并且基于各指标的协方差矩阵对其权重分别进行了设计。但是其分段精度和效率还有待改善。给出典型场景的仿真结果，如图1所示，可知分段点数量是实际分段点的数倍，并且分段准确度不高，其主要原因是模式不一致数据之间的相互干扰。

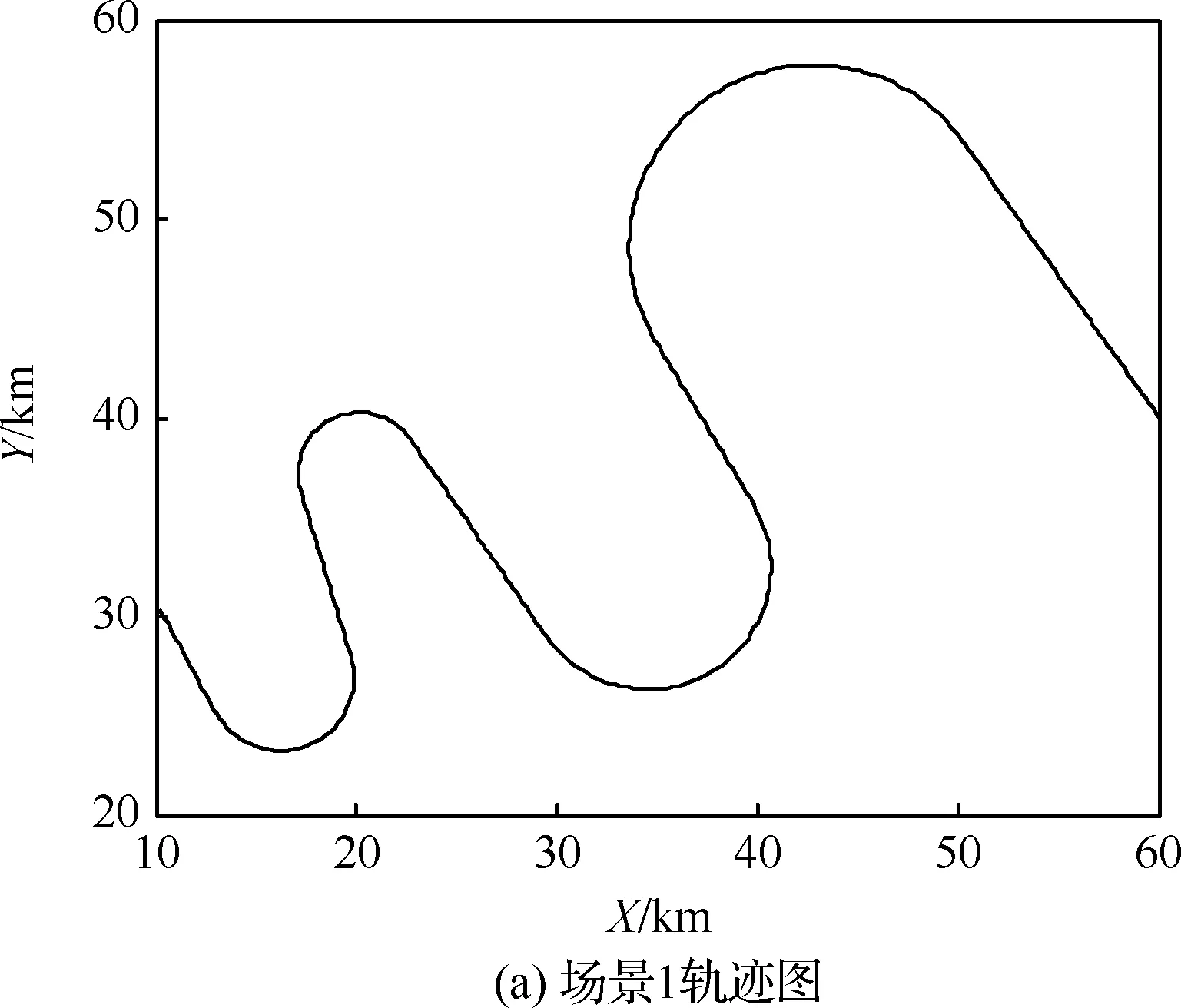
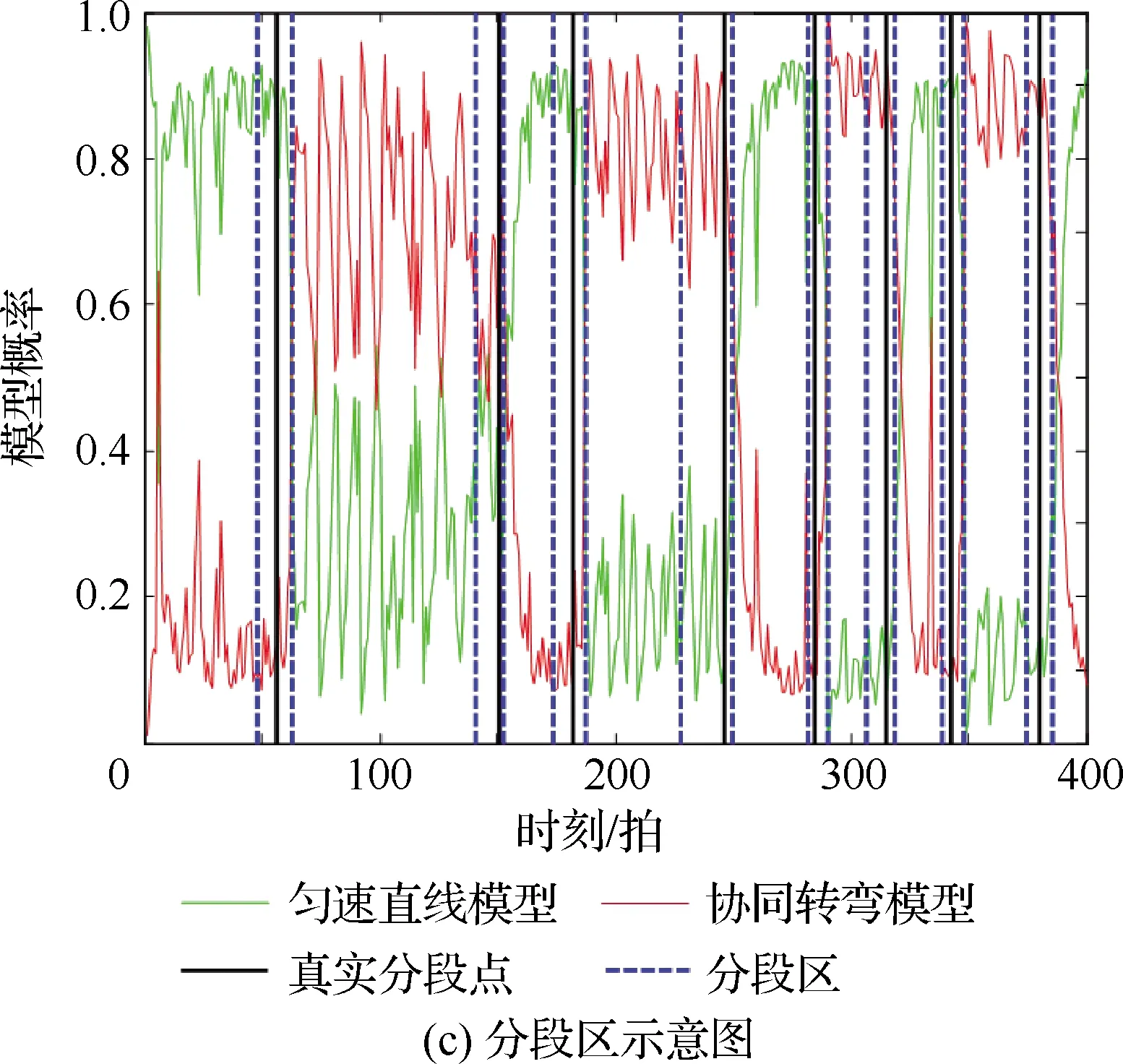
图1 文献[11]算法仿真结果Fig.1 Simulation results of algorithm of Ref. [11]

2 航迹的双层分段算法设计

在目标航迹分段识别中，有两方面原因会造成分段精度低：一量测是有误差的，直接判断存在高风险；二机动模型差异小，不易识别模式变化。如图2所示，本文提出了双层精细化航迹分段框架来提高轨迹分段的精度及效率，预分段层利用基于IMM算法检测目标运动过程中的模式切换，完成航迹预分段，得到目标模式变化明显区域的预分段点；再分段层利用改进的STI算法对模型差异小的非预分段区航迹进行回溯迭代优化再分段，得到更为精细的分段点。该框架具有从粗到精的航迹分段处理能力，实现了对于机动目标航迹的精细化分段识别，达到提高分段精度和降低迭代优化时间的目的。

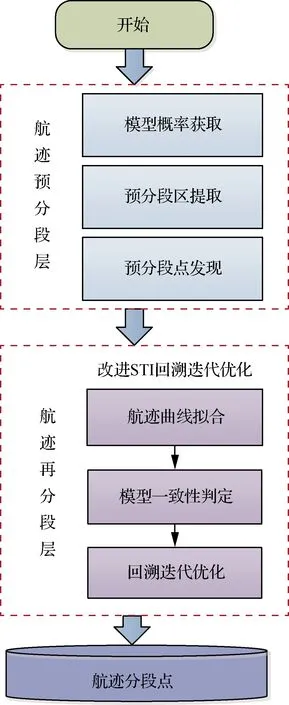
图2 基于双层分段的目标航迹分段框架流程图Fig.2 Block diagram of target flight track segmentation algorithm based on two-layer segmentation

2.1 预分段点提取

考虑航迹数据为一个带观测噪声的时间序列Z={z(1),z(2),…,z(K)}，系统状态的动态演化方程为

x(k)=F[ω(k-1)]x(k-1)+Γ(k-1)v(k-1)

z(k)=Hx(k)+Vk

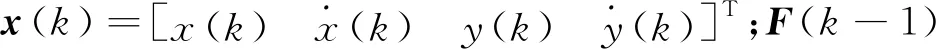
为了实现带有观测噪声的航迹数据的分段识别，在航迹预分段层，首先通过多模型估计方法对航迹位置观测数据进行滤波以获取模型概率；然后根据模型概率确定模式变化明显的预分段区；最后利用其两端的非预分段区数据对预分段区进行划分从而发现预分段点。为实现带有噪声的航迹分段，预分段层的算法和具体设计见算法1。

算法1 航迹预分段层算法1.输入量测值Z={z(1),z(2),…,z(K)}和上一时刻的状态估计值^xi(k-1k-1),i=1,2,…,N。2.基于IMM算法输出模型概率μj(k)。3.设置非单调变化阈值为δth见式(1),如果模型变化次数δ>δth则停止回退。4.确定预分段区。

算法1主要包含预分段区提取和预分段点发现策略这部分内容，详细设计如下：

寻找预分段区时，首先根据模型概率判定运动模型类别，若运动模型类别发生突变，则进入剔除异常点步骤，判断该点前后模型类别是否与当前时刻一致，均不一致则为异常点，否则在窗长为L的区间内寻找同类模型并计算该类模型的数量占比值，若占比低于阈值，视为异常值。若前后一致性检验和模型占比检验均通过则为预分段区终止点，接着回退寻找预分段区起始点。回退原则为回退至概率刚刚开始连续单调变化的时刻，但是由于存在噪声，实际模型概率在预分段区并不严格单调，因此设置非单调变化阈值，该阈值与回退长度成正比，定义为

δth=δE×(ki,ni-k)δE∈(0,1)

(1)

式中：i表示第i个预分段区；ni表示第i个预分段区数据点个数；ki,l表示第i个预分段区的第ni个数据点；E表示模型概率非单调变化次数；δE表示模型概率非单调变化次数阈值。

一旦非单调变化个数到达阈值，则停止回退，对应点就是预分段区起始点。因此，根据起始点和终止点得到第i个预分段区Si=[ki,1,ki,2,…,ki.ni]。将分段后的两段数据分别加入到两段非预分段区中，得到两个时刻段：

Sfront,l=[ki-1,li-1,ki-1,li-1+1,…,ki.l]

Sback,l=[ki,l+1,ki,l+2,…,ki+1,1-1]

其中：ki-1,li-1表示第i-1个预分段区的分段时刻；ki+1,1表示第i+1个预分段区第一时刻。预分段点发现策略使用对航迹数据进行非线性最小二乘拟合的方法，遍历该区间所有数据点作为假设分段点，选择对数似然概率最大点作为预分段点，分段点的计算方法如下。

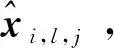
步骤2根据拟合区间为预分段区和非预分段区的合并区间，数据量较大，所以航迹拟合结果与真值接近，拟合残差近似满足：

那么，第i个预分段区以该段第l个点作为假设分段点时，其分段点对数似然概率可以表示为

步骤3求解得到预分段点在预分段区的坐标li为

最后得到预分段点为ki,l。

2.2 航迹再分段点提取

完成预分段过程后，需要遍历非预分段区的航迹数据点进行分段点的精细化选取，进而提高分段精度，进一步降低迭代优化时间，改进的STI算法回溯迭代优化算法描述见算法2。

算法2 改进STI算法回溯迭代优化1.输入预分段量测信息ZSN={zSN(1),zSN(2),…,zSN(LN)}。2.求解^Θk=argminΘkc(^XSN,ZSN,SSN-1),得到模型参数估计值为^Θk,得到^XSN={^xSN(1),^xSN(2),…,^xSN(LN)}。3.模型一致性判定:如果该段拟合结果的均方根误差Ki超过航迹观测噪声对应标准差的KRMS倍,则将最新点设定为分段点,跳转到4;如果最近的Lh个航迹数据不再有较好的拟合精度,也将最新点设定为分段点,跳转到1。4.回溯迭代优化:如果SN-δS-1和SN-δS之和,小于拟合代价式(2)的Km倍,则不分段,继续优化;反之,则分段,跳至1。5.n=N时,完成航迹优化分段。

算法2主要分为航迹曲线拟合、模型一致性判定和回溯迭代优化3部分内容。

2.2.1 航迹曲线拟合

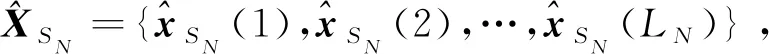
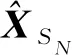
其中：KX为用于权衡分段点连续性与拟合准确性的调节参数。该函数输入通过扩维加入连续性指标求取所需要的航迹段连接点的位置和角度信息，若拟合航迹段时刻区间为[a,b]，则拟合输入XExpand为

XExpand=

函数拟合代价通过扩维加入连续性指标，即拟合代价为

2.2.2 模型一致性判定

模型一致性判定流程图如图3所示，判定条件主要有两个：

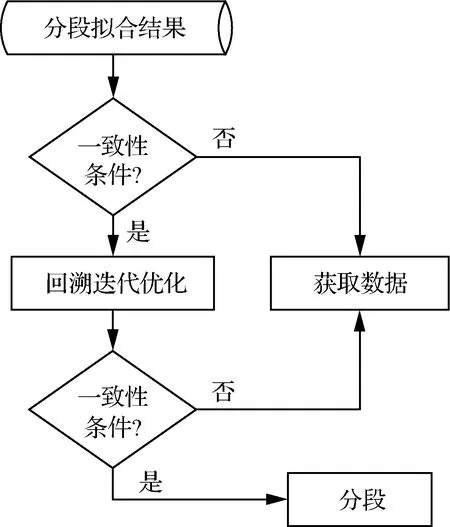
图3 模型一致性判定流程图Fig.3 Flow chart of model consistency determination

1) 若该段已有数据的拟合结果的均方根误差(Root Mean Square，RMS)超过航迹观测噪声对应标准差的KRMS倍，则将最新点设定为分段点。

2) 若最近的Lh个航迹数据不再有较好的拟合精度，也将最新点设定为分段点。

具体表现为该段中最新Lh个航迹数据的平均误差超过该段之前所有数据对应平均误差的KΔ倍，其中Lh∈{1,2,…,Lmin}，否则当本段数据长度小于该“尾巴”长度时，该条件不能生效。

2.2.3 回溯迭代优化

带时滞的回溯迭代优化框图如图4所示。核心部分为优化分段与合并分段2个部分。在创建新分段之前，需要将分段列表中最近的δS个分段重新优化调节分段点。由于发生在较久远之前的分段对现在的目标分段影响很小，δS一般取值为2或者3。需要注意的是优化分段SN-δS-1和SN-δS的代价函数包括了2个分段的2个连续性代价，分别对应2个分段的段首点的连续性代价。若分段SN-δS的段末为k时刻，则有

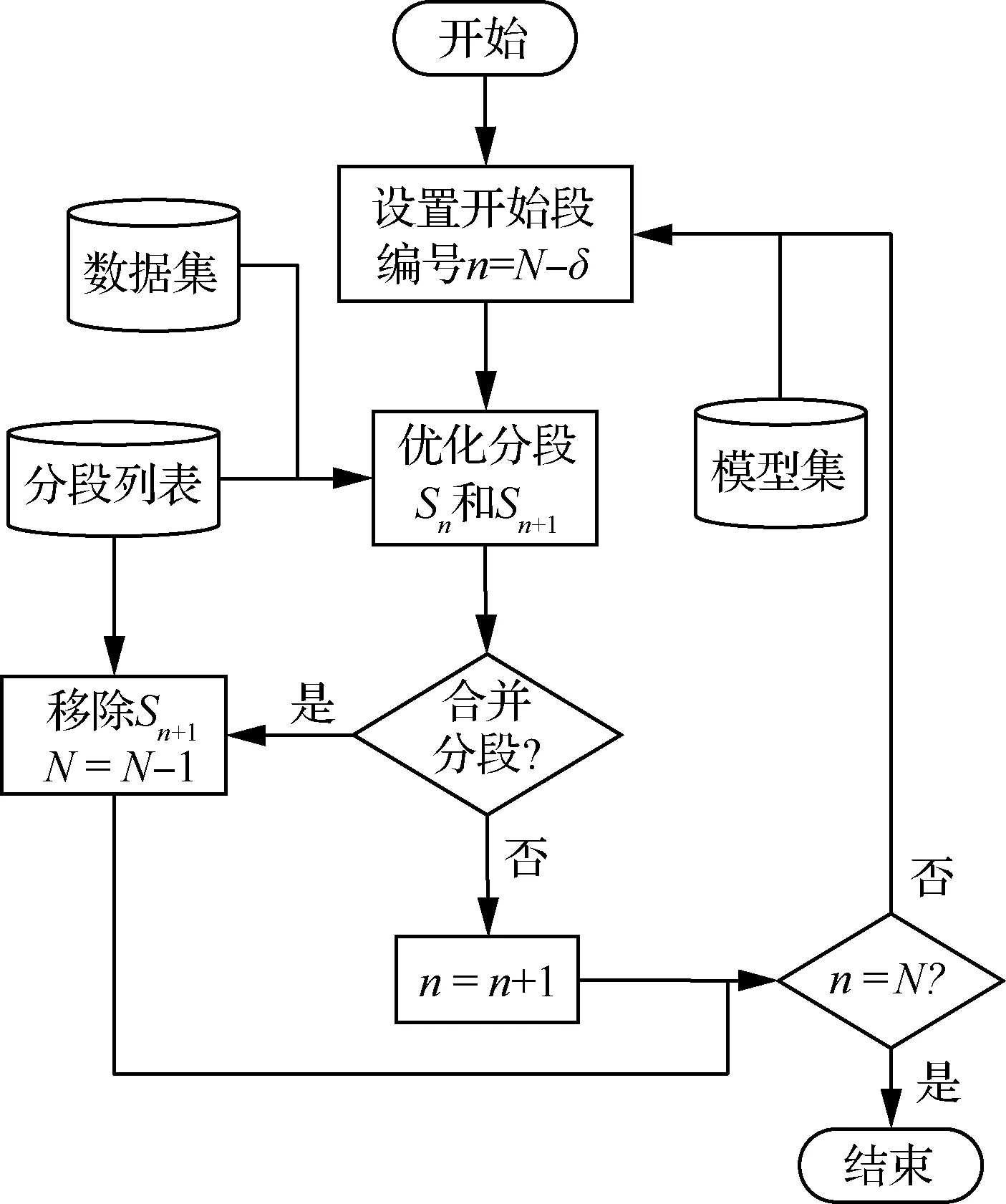
图4 迭代优化分段框图Fig.4 Block diagram of iterative optimization

若拟合航迹段时刻区间为[a,c]∪[c,b]，则拟合输入XExpand为

函数拟合代价通过扩维加入连续性指标，即拟合代价为

(2)

设置合并条件为合并后分段的代价小于原始2个分段各自代价之和的Km倍，参数Km一般取值为1.1或者1.2。将分段SN-δS-1和SN-δS合并之后，生成了新的分段SN-δS-1。接着继续优化分段SN-δS+1和SN-δS+2、分段SN-δS+2和SN-δS+3直到优化到最新分段。

3 实验验证

为了验证算法性能，本文实验验证包含两部分：仿真轨迹数据验证以及实际民航客机飞行轨迹数据验证。

3.1 仿真轨迹数据验证

3.1.1 场景设置

本文仿真选择文献[10]的测试想定，该想定包括2种场景，囊括了直线运动、缓慢转弯及强机动等典型的运动模式，参数取值如表1所示，符合目标实际运动特点：

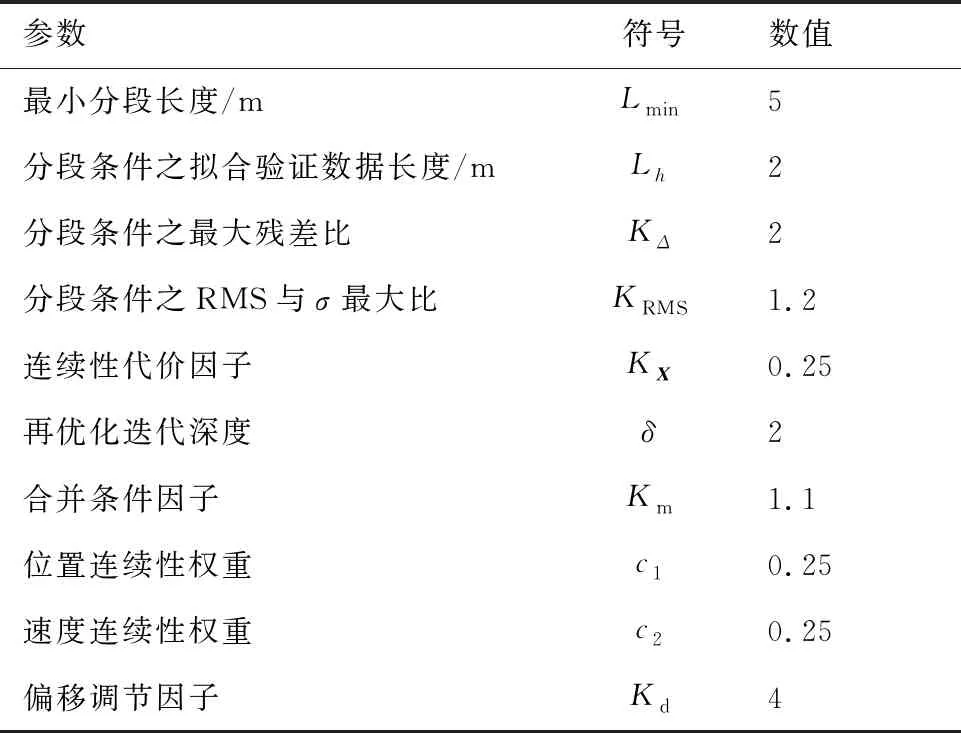
表1 算法参数取值Table 1 Simulation verification parameter values

1) 场景1(缓慢机动)：航迹场景轨迹图及其转弯角度分别为图1(a)和图5，目标进行了连续4次180°转弯，转弯角速度分别为1.87、-2.8、5.6、 -4.68 (°)/s，对应时间段分别为[56,150]、[182,245]、[285,314]、[343,379] s。目标初始位置为[60 000,40 000] m,初始速度为[246,-172] m/s，并且全程400 s期间速度一直维持300 m/s。

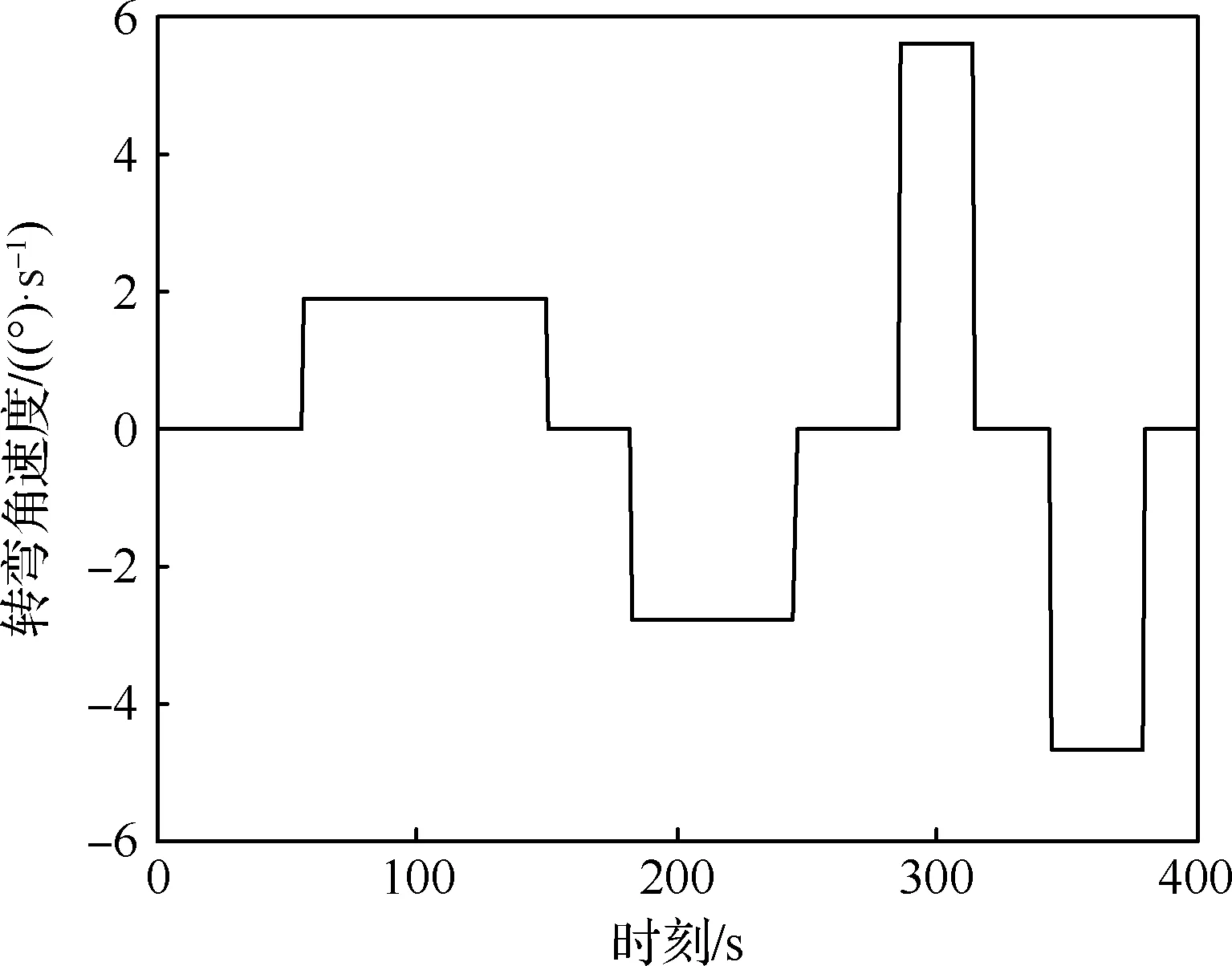
图5 场景1的转弯角速度图Fig.5 Turning angle velocity of Scenario 1

2) 场景2(强机动)：航迹场景轨迹图及其转弯角度分别为图6(a)和图6(b)。仿真中给出了高转弯角速度的强机动目标轨迹，执行了转弯角速度为10、-25、35、10、-25、35 (°)/s的协同转弯机动，依次持续持续时间分别为7、10、6、6、10、6、5 s。这个目标航迹的初始朝向角为0°，初始位置为[0,0] m，初始速度为11.252 m/s。

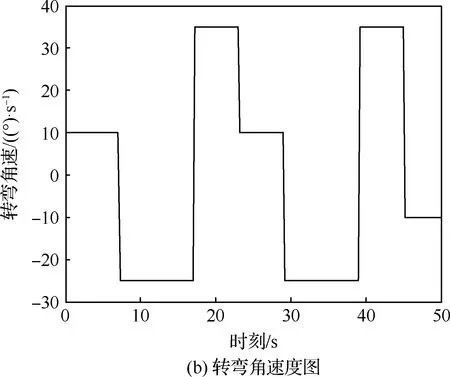
图6 场景2Fig.6 Design of Scenario 2

IMM算法求取模型概率是以CV和CT组合运动作为例子，其中状态转移矩阵如下：

对于CT模型：

F(k-1)=

对于CV模型：

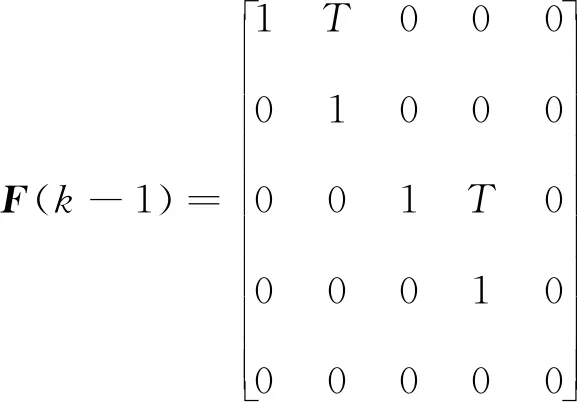
式中:ω(k)表示CT模型k时刻的转弯角速度；ξ=sinω(k-1)T；ζ=cosω(k-1)T；

3.1.2 性能评估

其中：改进度定义为

给出场景1和场景2的典型仿真结果：

场景1T=1 s，σx=σy=85m

图7～图10给出了2个仿真场景中多次仿真结果，图7和图9自上而下蓝色、粉色及绿色为实验中的估计分段点，图8和图10自上而下蓝色、粉色及绿色线条为转弯角速度误差多次仿真结果。由于采样周期的选取受运动平台的影响很大，比如：场景1是缓慢转弯运动的采样周期可以选T=2 s和1 s，但是对于强机动场景采样周期则减小至T=0.5 s和0.25 s，具体的采样周期的选取规则参考文献[10]，分段识别算法在多个仿真场景下的性能比较汇总如表2所示。

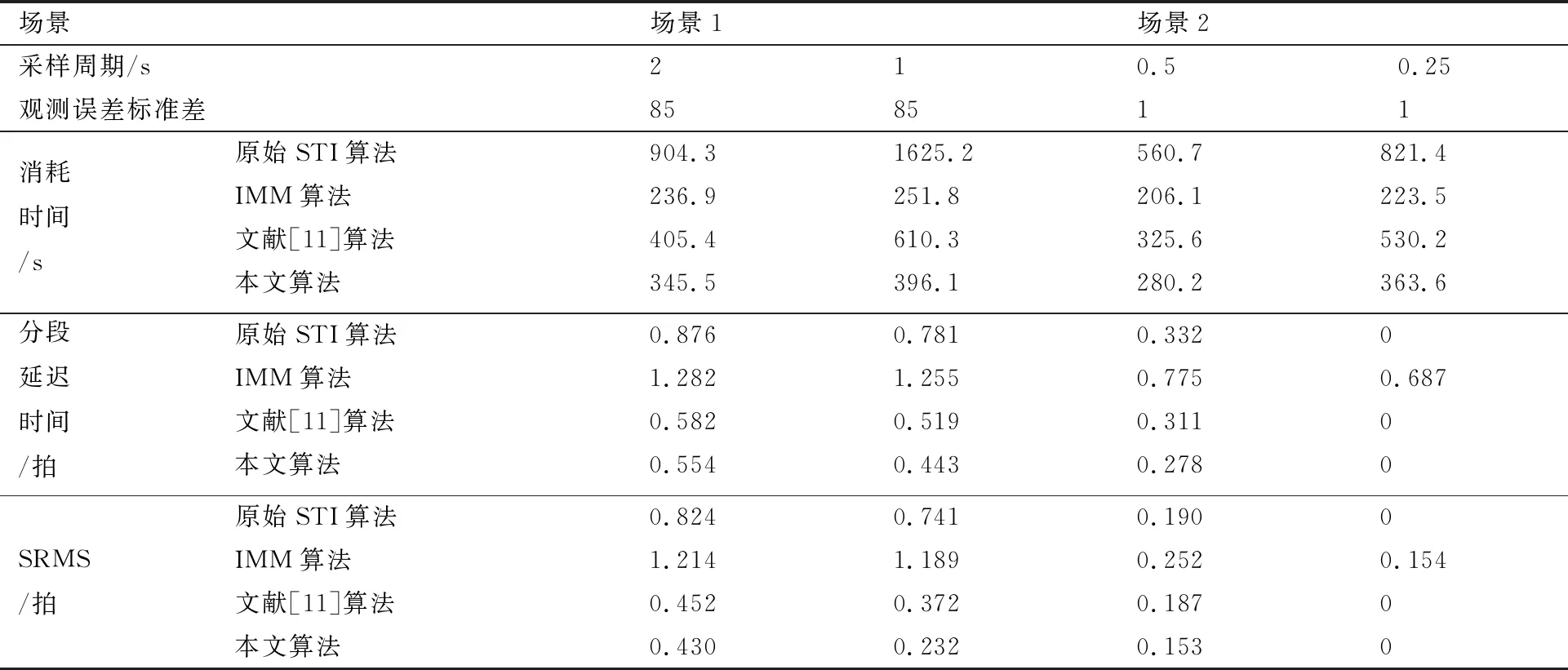
表2 多仿真场景性能比较

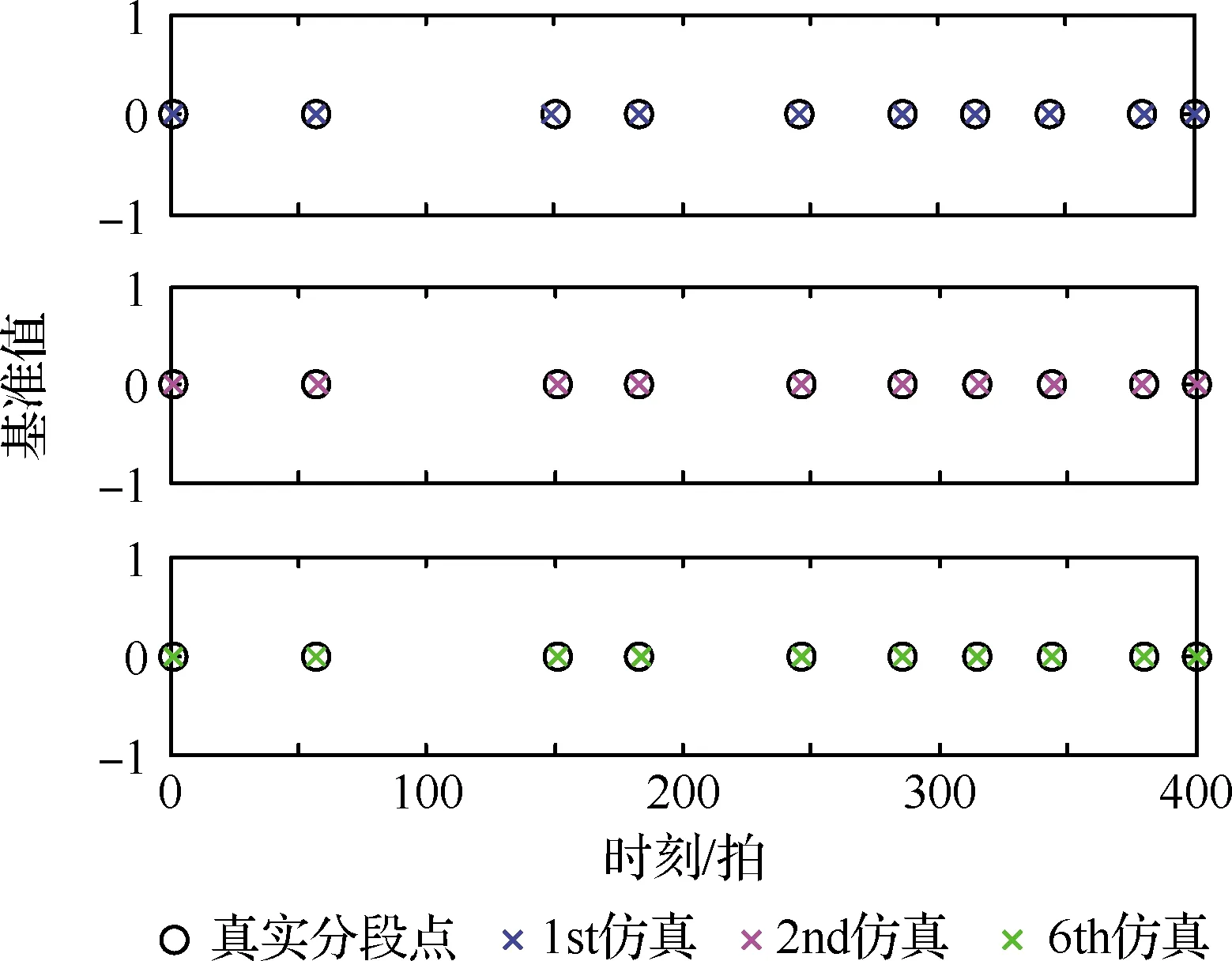
图7 场景1估计分段点与真值多次仿真结果汇总图Fig.7 Summary diagram of multiple simulation results of estimates of cutting points and true values of Scenario 1

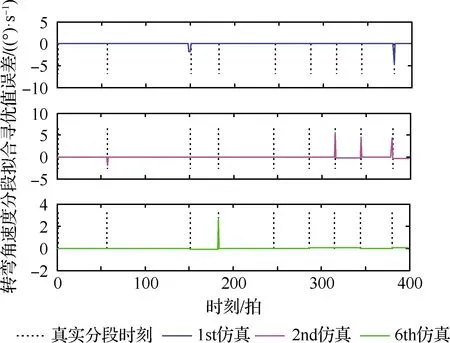
图8 场景1转弯角速度误差多次仿真结果汇总图Fig.8 Summary diagram of multiple simulation results of error of turning angle velocity of Scenario 1

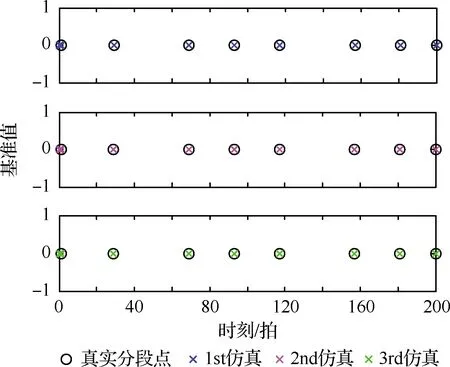
图9 场景2估计分段点与真值多次仿真结果汇总图Fig.9 Summary diagram of multiple simulation results of estimates of cutting points and true values of Scenario 2

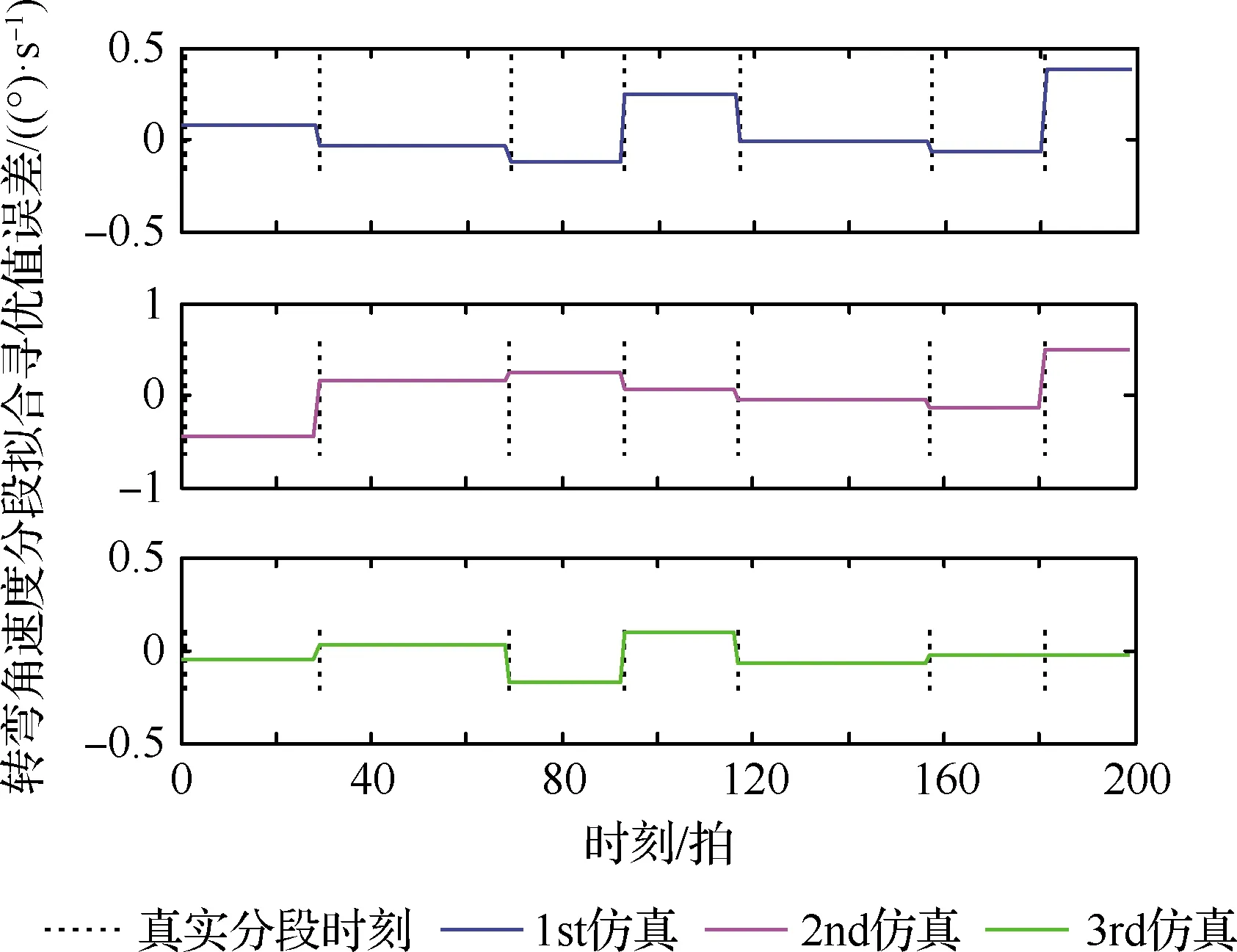
图10 场景2转弯角速度误差多次仿真结果汇总图Fig.10 Summary diagram of multiple simulation results of error of turning angle velocity of Scenario 2

场景2T=0.25 s，σx=σy=1m

将本文所提算法与对比算法在典型场景1和场景2下的运行结果进行分析，在不同采样周期下，本文算法的分段延迟时间和SRMS均优于对比算法。需要指出的是，虽然本文算法与IMM算法相比消耗时间相差不大，但是由于增加了再分段层，在分段精度方面提升显著，这是由于IMM算法对于模式切换不明显的区域识别效果较差，本文算法在没有增加过多时间消耗的情况下分段延迟时间和SRMS的性能指标均有很大提升。对比其他典型算法，本文算法不仅减少了消耗时间，而且明显提高了分段精度，同时在表3中给出了改进程度。

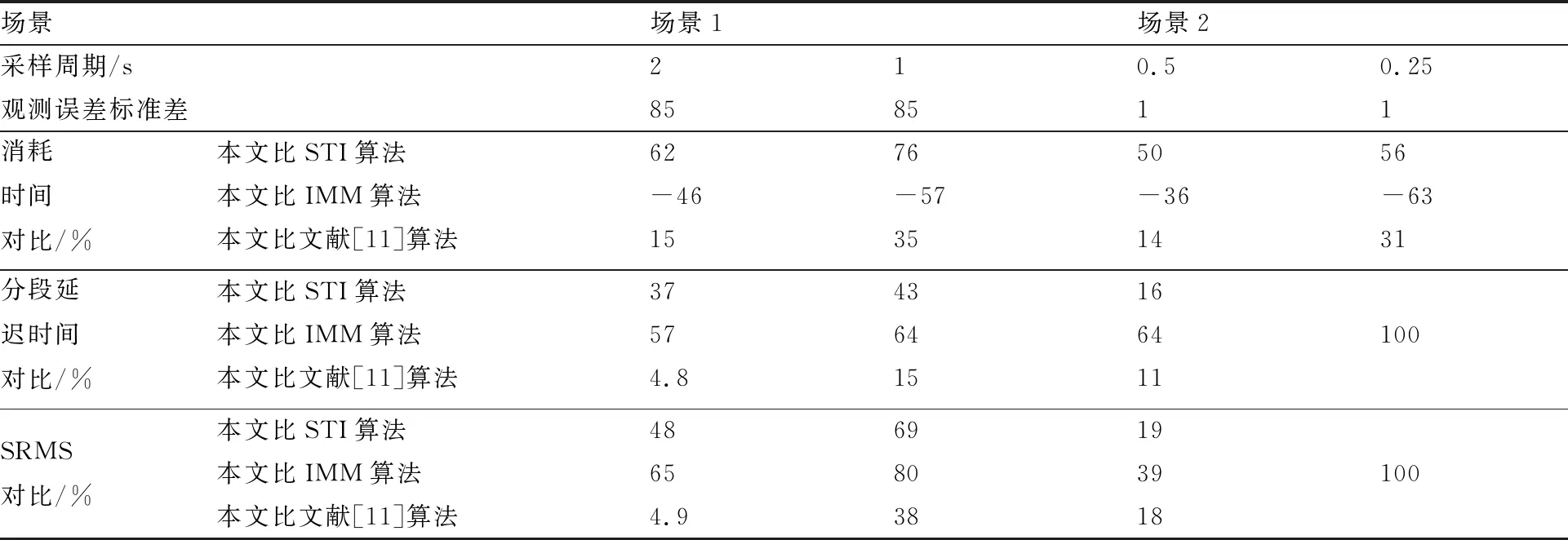
表3 性能比较汇总表Table 3 Summary of performance comparison

3.2 实际民航客机飞行轨迹数据验证

本文采用实际民航客机的飞行轨迹数据来进行验证。图11展示了从FlightAware下载的中国国航CA1301航班飞行轨迹的末端，其中黑色虚线为客机飞行航迹，经过3次转弯到达广州白云机场。红色圆圈为本文算法检测到的轨迹转弯点，也就是本文的分段点，该航迹中3次转弯位置均被准确识别。由此可知，本文算法可以有效识别出目标在运动过程中模式发生变化的位置，进而将航迹准确分段，为进一步判断目标行为意图提供支撑。

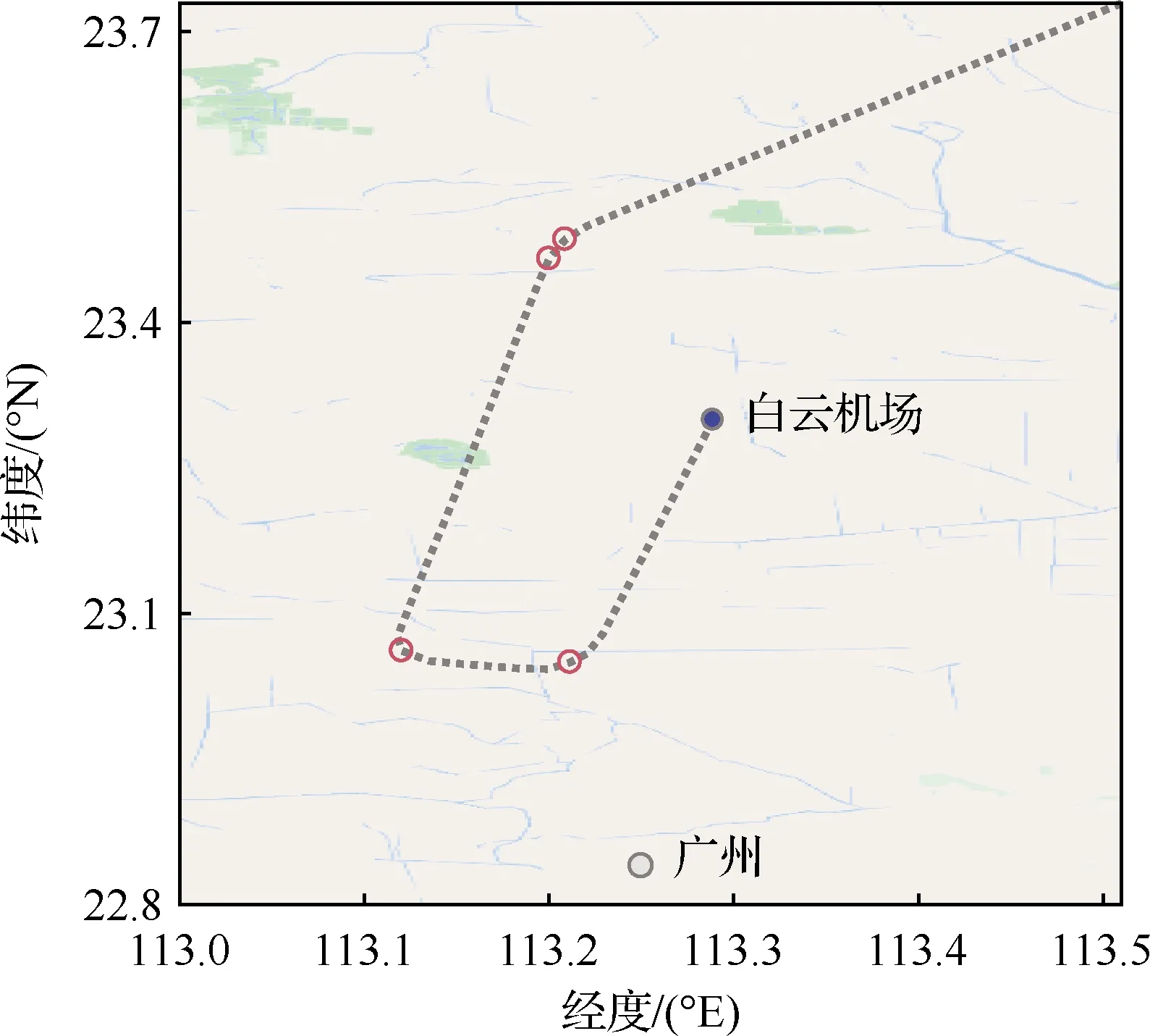
图11 客机飞行轨迹分段识别结果Fig.11 Results of segment recognition of airliner flight trajectory

4 结 论

本文重点研究了双层精细化航迹分段框架，首先，在预分段层利用IMM算法得到每一时刻的模型转移概率，用于发现模式变化明显的预分段区，进而得到目标模式变化明显区域的预分段点；然后，在分段层利用改进的STI算法对模型差异小的非预分段区航迹执行回溯迭代优化再分段，得到精细化的分段点。该框架具有从粗到精的航迹分段处理能力，实现了对于机动目标航迹的精细化分段识别，有效减少分段时间，提高了航迹分段精度。典型仿真场景测试也验证了所提算法的有效性。