一种基于偏好MOEA的卫星地面站资源多目标优化算法
2021-07-05孙刚陈浩彭双杜春李军
孙刚,陈浩,彭双,杜春,李军
国防科技大学 电子科学学院,长沙 410073
人造卫星按预定轨道绕地球飞行,利用其空间优势在气象预报、环境监测、资源普查、通信导航以及军事侦察等领域发挥着重要作用[1-2]。卫星平台的正常工作离不开卫星地面站的支持,如对卫星的跟踪、测量、控制以及有效载荷数据的下传等,这些操作都需要卫星与地面站建立通信通道。卫星与地面站能否建立通信通道取决于二者之间的空间相对位置。对于某地面站,可根据卫星的轨道信息以及地面站的地理位置信息(经度、纬度、海拔)计算出指定时间段内的一系列可通信时间段,称为卫星相对于该地面站的可见时间窗口。可见时间窗口长度与卫星的轨道高度相关,通常低轨卫星与地面站的可见时间窗口长度会短于中高轨卫星的可见时间窗口。
随着各国航天事业的迅速发展,在轨卫星数量不断增长,但卫星地面站的建设相对滞后,这种发展上的不平衡导致了星地通信中地面站资源相对匮乏。一般而言,地面站中一套数据传输设备在某一时刻只能服务于一颗卫星。在多卫星、多地面站情况之下,多颗卫星与同一地面站的可见时间窗口可能发生重叠,形成多星进站冲突;同时,同一颗卫星也可能同时与多个地面站形成可见时间窗口。因此,需要从全局角度优化选择合适的地面站资源为卫星提供数据传输服务。
如图1所示,卫星SAT-1、SAT-2、SAT-3同时进入了地面站GS-1的数据传输范围,其与地面站GS-1的可见时间窗口重叠,发生多星进站冲突,地面站GS-1只能选择其中之一提供服务。同理,SAT-2、SAT-3和SAT-4对于地面站GS-2发生多星进站冲突。另一方面,卫星SAT-2对地面站GS-1和GS-2同时可见,可选择其中之一进行数据传输服务。

图1 多地面站多卫星数据传输问题示意图Fig.1 Illustration of multiple satellites data transmission problem among multiple ground stations
如何合理规划星地通信时间使得更加充分地发挥卫星地面站资源的整体效益,即为卫星地面站资源规划所研究的问题,该问题得到了国内外学者的高度关注。当前的研究工作主要集中在两个方面:一是对于问题性质及复杂性的研究;二是对于问题求解方法的研究。在问题性质及复杂性这个研究方向上,Vazquez和Erwin[3]的研究工作具有典型性,该项研究不仅对问题的特征、约束条件及复杂性进行了分析,而且在理论上证明了问题的NP-hard特性。在问题求解方法上,大致可分为精确求解方法和启发式求解方法两个类型。在精确求解方法中,ILP[4](Integer Linear Programming)以及MIP[5-6](Mix Integer Programming)具有代表性,但随着问题规模的增大,巨大的参数量和约束条件使得这类方法在求解问题时变得异常困难。针对精确求解方法的不足,结合启发式策略或松弛技术的算法被引入到卫星地面站资源规划问题中,用以得到问题近似解而非全局最优解,从而较大地降低了问题求解的计算复杂度,但其优化性难以保证。为了在可接受计算时间内求得问题的满意解,基于元启发算法的卫星地面站资源规划方法得到了越来越多的关注。元启发算法提供了一种通用的启发式元信息对搜索进程进行引导,从而克服了针对特定问题构建特定启发式策略的困难,取得了较好的效果。典型的用于卫星地面站资源规划问题的元启发算法包括:模拟退火方法[7](Simulated Annealing, SA)、进化计算方法[8-10](Evolutionary Algorithm, EA)、禁忌搜索方法[11](Tabu Searching,TS)、蚁群搜索方法[12-13](Ant Colony Algorithm, ACA)等,但这些算法仅以单个优化目标作为规划方案的评价准则。
实际上,卫星管理机构所关注的优化目标往往不止一个,如任务规划失败率、天线负载平衡度、任务相对于参考时间的集中度等,这些优化目标之间往往存在一定的冲突,即提高某个优化目标的效益往往会导致另一些优化目标效益降低。因此,卫星地面站资源规划问题本质上是一个多目标优化问题。目前,主流的求解多目标优化问题的方法是MOEA(Multi-Objective Evolutionary Algorithm)。相关研究工作已广泛应用于数据挖掘[14]、移动网络规划[15]、物流配送[16]、通信与网络优化[17]等领域,但将卫星地面站资源规划问题抽象为多目标优化问题的研究工作还相对较少,不成体系。Song等[18]以最大化任务规划收益和最小化任务规划失败率为优化目标,将学习引导机制与NSGA-II[19](Non-dominated Sorting Genetic Algorithm-II,该算法基于Pareto支配关系对进化种群进行分层并根据层的优先级构建下一代种群,通过聚集距离维持解群体的分布性和多样性)算法相结合实施多目标优化,但优化目标之间存在正相关性。Du等[20]将MOEA与LS(Local Searching)相结合构建了一个算法框架用于求解卫星地面站资源规划的双目标(最小化任务规划失败率、最大化天线负载平衡度)优化问题,实验表明,基于该框架的算法在多个性能指标上优于本体算法,但其最低任务规划失败率在多数实验场景下均高于10%。
针对卫星地面站资源规划的多目标优化问题,传统的MOEA首先求得一系列在优化目标上的非支配解,决策者再根据实际需要(偏好信息)从中选择一组符合决策者期望的解,这个过程由“优化”和“决策”两步完成。基于偏好的MOEA将“优化”和“决策”有机结合,利用决策者提供的偏好信息引导算法搜索方向,使算法着重搜索能产生符合决策者偏好的部分Pareto解。Jaimes等[21]利用ASF(Achievement Scalarization Function)定义了一个ROI(Region of Interest)并提出Chebyshev支配关系用于解决机翼形状优化问题,其中Chebyshev支配关系定义为:ROI之内的个体根据Pareto支配关系排序,ROI外部的个体根据ASF函数值排序。Mahbub等[22]提出基于目标区域的pNSGA-II(Preferred-region NSGA-II)算法并将其用于能源系统优化,该算法以某个优化维度上的多个区间表达偏好,以个体与偏好区间在这个维度上的距离为标准将个体与偏好区间关联,在NSGA-II算法框架之内结合个体与偏好区间的距离实施优化。Oliveira等[23]提出了EvABOR-III(Evolutionary Algorithm Based on Outranking Relation-III)算法用于电网配置,该算法利用决策者设定的一组参数(一致性指数、失调指数、置信度等)定义outranking关系并将其引入MOEA的交叉、变异算子之中,在构建下一代种群时优先考虑Pareto支配关系,当基于Pareto支配关系选择的种群不满足要求时利用outranking关系予以处理。李龙梅[24]提出了T-MOEAs(Target region based Multi-Objective Evolutionary Algorithms)并将其用于对地观测卫星任务规划的多目标优化问题,该算法以点或区域表达决策者的偏好信息,在构造下一代种群策略中优先考虑Pareto支配关系以引导种群向Pareto前沿进化,其次考虑个体与偏好信息之间的Chebyshev距离等级以引导种群向偏好点或区域进化。目前,将偏好MOEA用于卫星地面站资源规划问题的研究尚未见报道。
在卫星地面站资源规划问题中,决策者的偏好信息可通过历史规划方案获取。利用偏好MOEA可以直接求出决策者感兴趣的部分Pareto解。考虑到偏好MOEA的这种优势,论文构建了基于领域知识的启发式策略,并将其与偏好MOEA相结合,用于求解卫星地面站资源规划的多目标优化问题。论文的主要贡献在于:
1) 将卫星地面站资源规划问题建模为一个偏好多目标优化问题,并将领域知识抽象为偏好信息的设定,进一步提升了问题求解的针对性。
2) 提出了一种基于领域知识的启发式策略,能够与偏好MOEA有效结合,从而更进一步提升了问题求解的优化性。
3) 基于广泛采用的benchmark数据集AFSCN(Air Force Satellite Control Network)(可通过http:∥www.cs.colostate.edu/sched/data.html下载 )设计了相关实验,实验结果表明,相比于现有方法,论文提出的方法能够根据决策者指定的偏好信息更有针对性地求解符合决策者偏好的解,从而验证了论文提出的方法的可用性和有效性。
1 数学模型
卫星地面站资源规划问题是一个多约束条件下的复杂优化问题,旨在解决多卫星、多地面站的场景下如何合理规划星地通信时间使得卫星管理机构所要求的多个优化目标效益最佳。在本节中,首先针对问题进行必要的假设和形式化描述;然后构建目标优化函数及偏好表达;最后对于问题的约束条件进行描述和建模。
1.1 问题形式化描述
根据工程实践和现行的技术条件,论文做合理假设如下:
1) 不考虑卫星及地面站设备的各类突发事件,认为在规划周期内所有的地面站设备以及卫星均能正常工作。
2) 参与规划的地面站天线均能无差别地支持各类卫星任务。
3) 同一天线在任意时刻至多只能支持一颗卫星的任务。不失一般性,若天线支持多通道工作模式,则将其视为多套单通道天线同址布署。
根据以上假设条件对卫星地面站资源规划问题进行数学建模,为了便于描述,首先给出模型中相关符号的定义,具体如下:

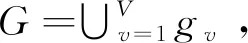

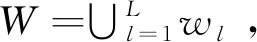
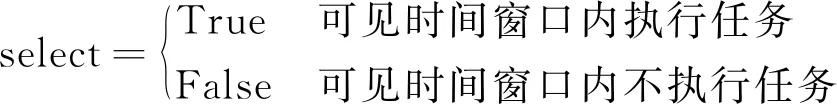
(1)
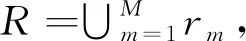
R_si为卫星si在规划周期内的任务需求,∀si∈S,R_si={rm∈R|rm.sID=si.sID},|R_si|表示需求数量,即在规划周期内需要对卫星si规划|R_si|次任务。

[ST,ET]为规划周期,其中ST表示规划开始时间;ET表示规划结束时间。
根据以上描述可知,问题的决策变量包括布尔逻辑变量select、r_ts时间变量以及r_te时间变量,其中select变量决定在哪些可见时间窗口内执行任务,而r_ts变量以及r_te变量分别决定在可见时间窗口的哪一个时间点开始与结束任务。
1.2 目标函数及偏好表达
论文涉及的优化目标包括任务规划失败率和天线负载平衡度[20],目标函数的数学描述形式为
Y=min{y1,y2}
(2)
1)y1表示任务规划失败率,其物理含义为无法安排的数据传输任务数量占总任务数量的百分比
(3)
式中:|F|表示规划结果集中的任务数量,其数值为N;|R|表示任务集中的任务数量,其数值为M。
2)y2表示天线负载平衡度,其物理含义为天线工作时长的标准差与天线平均工作时长的比值:
(4)
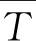
(5)
(6)
偏好信息的引入方式有多种,文献[24]将其分为以下类型:参考点方式、参考方向方式、偏好函数方式、目标区域方式、trade-off方式、目标比较方式、候选解比较方式、outranking方式等。其中基于参考点方式引入偏好信息的应用最为广泛,这种方式由决策者在目标空间中指定一个点表示其在每一个目标函数上的期望值,从而引导偏好MOEA求出靠近参考点的部分最优解。论文以参考点方式将偏好信息引入偏好MOEA,具体表达为
Pref=[y1-ref,y2-ref]
(7)
式中:y1-ref表示决策者在目标函数y1上的期望值;y2-ref表示决策者在目标函数y2上的期望值。y1-ref、y2-ref的值可根据历史规划方案中的统计值进行设置,在不同的应用场景下其取值有所不同,例如在日常的卫星地面站资源规划中,决策者可能会选择一个相对折衷的数值,以兼顾任务规划失败率和天线负载平衡度,从而延长设备使用寿命;在执行重大保障任务时,决策者可能更加关注低的任务规划失败率,以最大限度完成任务。
1.3 约束条件
约束条件是保证规划结果合理性与可行性的关键所在,论文涉及的约束条件主要包括:
1) 天线唯一性约束:任意时刻,同一天线至多只能与一颗卫星建立通信通道。
2) 任务非冲突约束:同一天线相邻任务之间满足一定的时间间隔,即任务转换时间,以供设备及操作人员进行必要的准备工作。
3) 卫星唯一性约束:任意时刻,同一卫星至多只能与一个地面站天线建立通信通道。
4) 可见时间窗口约束:任务起止时间要位于相应的可见时间窗口之内。
5) 任务最低持续时间约束:任务的持续时间不低于任务所要求的最低持续时间。
6) 规划周期约束:任务起止时间要位于规划周期之内。
针对以上约束条件,其数学形式描述如下:
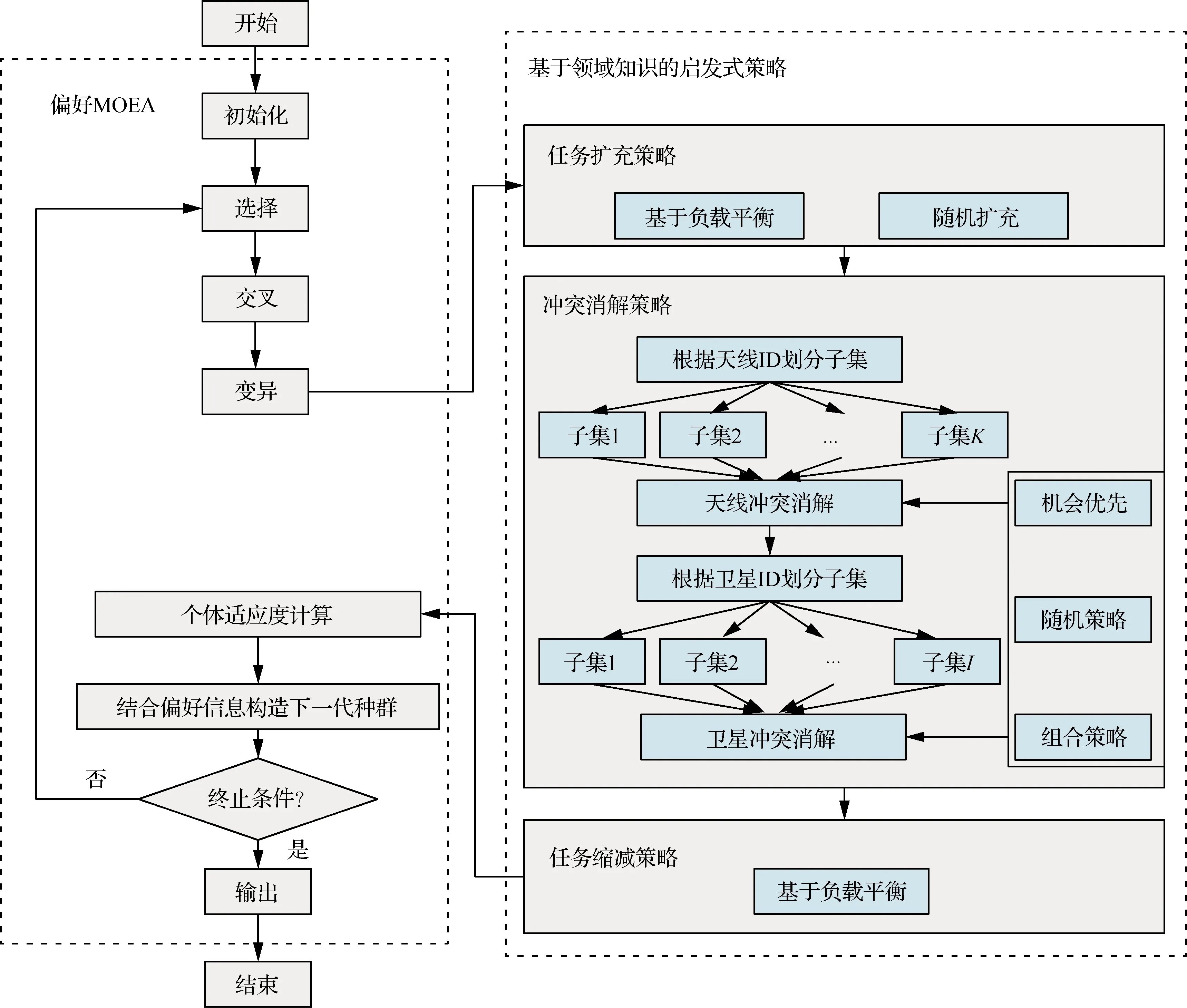
1) ∀fu,fz∈F_ak,若fu.r_ts fz.r_ts>fu.r_te+fz.rID.tvert (8) 2) ∀fu,fz∈F,若fu.wID.sID=fz.wID.sID,则 [fu.r_ts,fu.r_te]∩[fz.r_ts,fz.r_te]=Ø (9) 3) ∀fu∈F,则 fu.r_ts≥fu.wID.ts且fu.r_te≤fu.wID.te (10) fu.r_te-fu.r_ts≥fu.rID.tmin (11) fu.r_ts≥ST且fu.r_te≤ET (12) 式(8)对应于天线唯一性约束以及任务非冲突约束;式(9)确保卫星唯一性约束得到满足;式(10)对应于可见时间窗口约束;式(11)和式(12)分别对应于任务最低持续时间约束以及规划周期约束。通过以上约束条件,可确保卫星地面站资源规划结果的合理性与可行性。 在本节中,首先将介绍卫星地面站资源规划问题的偏好MOEA框架;然后对于编码策略、交叉算子以及变异算子进行介绍;最后描述基于领域知识的启发式策略。 卫星地面站资源规划问题的偏好MOEA框架如图2所示。该算法框架主要包含两个部分:一是偏好MOEA部分,二是基于领域知识的启发式策略部分。其中,基于领域知识的启发式策略嵌入在偏好MOEA中的“变异”与“个体适应度计算”之间,通过启发式策略引导种群向优化目标函数值较好的方向进化。 图2 地面站资源规划问题的偏好MOEA算法框架Fig.2 Preference-based MOEA framework for satellite range scheduling problem 在偏好MOEA部分,由于在数学模型中采用了参考点偏好表达方式,因此选择基于参考点的偏好MOEA对问题进行求解。考虑文献[24]中T-NSGA-II、T-SMS-EMOA、T-R2-EMOA算法的性能优势,论文拟以这3种算法为基础嵌入基于领域知识的启发式策略求解卫星地面站资源规划问题。T-NSGA-II、T-SMS-EMOA、T-R2-EMOA算法分别以NSGA-II、SMS-EMOA[26](S-Metric Selection Evolutionary Multi-objective Optimization Algorithm)和R2-EMOA(R2-indicator Evolutionary Multi-objective Optimization Algorithm)为本体,在原算法基础上增加了一层排序规则,即Chebyshev距离等级,解个体Chebyshev距离等级的分配与其距参考点的Chebyshev距离大小有直接关系,Chebyshev距离越小则赋予的等级越高,那么被选择进入下一代种群的概率就越高,因此距离参考点Chebyshev距离越近的个体就越容易被保留下来。 SES-EMOA算法以最大化超体积空间为进化方向,超体积空间越大表明算法所求解集越逼近Pareto前沿,其中超体积空间定义为解集与参考点在目标空间中围成的体积,即 (13) 式中:Γ表示解集;Pref=[p1,p2,…,pΥ]表示参考点;Υ表示优化目标函数维度;Leb表示勒贝格测度。 R2-EMOA算法以最大化R2指标为进化方向,其他方面与SMS-EMOA基本相同,其中R2指标定义为 R2(Γ,Θ,P*)= (14) 当这个参考点设置为决策者的偏好时,生成的解就位于偏好信息附近的Pareto前沿,从而体现决策者的偏好。Chebyshev距离计算方法为 (15) 式中:Φ=[f1,f2,…,fΥ]表示解个体;Pref=[p1,p2,…,pΥ]表示参考点。基于领域知识的启发式策略部分详见2.3节。 算法的终止条件可依据问题的复杂性和现实需求设置,通常为算法运行时间或者进化代数。算法的输出结果为种群中的非支配个体以及对应的目标函数值。 编码策略即个体的编码方式,常用的编码方式包括二进制编码、实值编码以及排列方式。编码方式的选择与问题的数学模型相关,考虑到论文中数学模型的决策变量select为布尔类型,因此在编码方式上选择二进制编码最为合理。如式(1) 所示,select变量的取值决定了执行任务的可见时间窗口。 对于可见时间窗口wl,当wl.select取值为False时,可见时间窗口被编码为0;当wl.select取值为True时,可见时间窗口被编码为1。因此,个体编码方式可表示为 X={x1,x2,x3,…,xL} ∀i∈{1,2,…,L},xi∈{0,1} (16) 式中:L的数值等于可见时间窗口的数量。 交叉算子和变异算子:选择HUX[27](Half Uniform Crossover)交叉算子以及BF[28](Bit Flip)变异算子用于子代个体的生成。 由于个体编码方式为二进制编码,因此解空间的大小与编码长度有关,当编码长度为L时,解空间大小为2L,即随着编码长度的变化,解空间以2的指数次幂发生变化。当编码长度较长时,解空间将非常巨大,如果以均等的概率搜索全部解空间,将极大地降低算法性能。为了解决这个问题,论文引入基于领域知识的启发式策略,具体包括任务扩充策略、冲突消解策略以及任务缩减策略,这3种策略对于解空间的搜索范围如图3 所示。 图3 解空间搜索范围示意图Fig.3 Illustration of search scope of solution space 2.3.1 任务扩充策略 根据编码规则可知,个体编码与可见时间窗口select变量相对应,其中个体编码中数值为1的基因确定了一个可见时间窗口集合,即为潜在任务执行时间窗口集。在这个集合中,通常会存在两种典型特征:① 用于执行某卫星任务的可见时间窗口数量可能小于该卫星的任务需求;② 在任务规划过程中可能违背天线唯一性约束、卫星唯一性约束以及任务非冲突约束等条件。任务规划失败率一部分源于特征①,另一部分源于针对特征②进行的冲突消解操作。为了降低任务规划失败率,可通过任务扩充策略使得扩充后的潜在任务执行时间窗口集合不存在特征①,且提供一定的冗余以降低特征②对任务规划失败率的影响。 图4 基于负载平衡的任务扩充策略示意图Fig.4 Illustration of tasks expansion strategy based on load-balance 算法伪代码如算法1所示,其中:si_req为卫星si的任务需求数量;η为扩充系数;|Wsi_sel|表示W中select变量为True的属于卫星si的可见时间窗口数量;|Wsi_nsel|表示W中select变量为Flase的属于卫星si的可见时间窗口数量。 算法1 任务扩充Algorithm 1 Tasks expansion 2.3.2 冲突消解策略 冲突消解策略以任务扩充策略处理后的潜在任务执行时间窗口集为输入,首先进行地面站天线冲突消解,以使得在该集合上规划的任务满足式(8)、式(10)、式(11)的约束条件;其次进行卫星冲突消解,以满足式(9)~式(11)的约束条件。 在地面站天线冲突消解中,以天线ID为依据将潜在任务执行时间窗口集划分为多个子集,子集的数量与天线的数量是一致的,针对每个子集进行冲突消解。在进行冲突消解时,借鉴了滑动窗口的思想,即在满足任务最低要求持续时间的前提下,任务的开始时间和结束时间可以在当前可见时间窗口内滑动。在初始化时,任务的开始时间和结束时间分别设置为当前可见时间窗口的开始时间和结束时间,在满足任务最低要求持续时间的前提下,可以在当前可见时间窗口内确定任务的开始时间滑动区域和结束时间滑动区域,如图5所示。 图5 滑动窗口示意图Fig.5 Illustration of sliding window 图5中,可见时间窗口wi的开始时间和结束时间分别为ts和te,该可见时间窗口内的任务在初始化时,任务的开始时间和结束时间分别设为ts和te。由于任务的最低要求持续时间为tmin,因此任务的最晚开始时间不能超过latest_r_ts(latest_r_ts=te-tmin),任务最早结束时间不能早于earliest_r_te(earliest_r_te=ts+tmin),即任务开始时间的可滑动范围介于ts和latest_r_ts之间,任务结束时间的可滑动范围介于earliest_r_te和te之间。 算法 2 天线冲突消解Algorithm 2 Conflicts-resolution of antenna 地面站天线冲突消解执行完毕后,为了确保任务规划结果不违背式(9)的约束条件,需要进行卫星冲突消解。在卫星冲突消解过程中要同时确保规划结果不违反式(10)、式(11)的约束条件。卫星冲突消解的过程与地面站天线冲突消解过程类似,不同之处在于卫星不存在任务转换时间,只要确保同一卫星在同一时刻至多与一个天线建立通信通道即可。 2.3.3 任务缩减策略 由个体编码确定的潜在任务执行时间窗口集经过任务扩充策略以及冲突消解策略处理后,形成了初步的规划方案。但是,在这个规划方案中,某些卫星的已规划任务数量或任务时长可能大于任务需求,这将造成卫星地面站资源的浪费,因此需要采取任务缩减策略以保证在规划方案中所有卫星的任务数量不超过其任务需求且任务时长也恰好满足要求。 在任务缩减策略中,对于规划方案中任务时长大于任务需求的情况,以任务开始时间为起始点进行截断;对于在规划方案中任务数量大于任务需求的卫星执行任务缩减操作时,论文使用了基于负载平衡的缩减方式,这种缩减方式通过计算执行某卫星任务的各天线的工作时长,选择工作时长最大的天线所对应的该卫星的任务进行删除,直至满足该卫星的任务需求,从而使得负载平衡度这一优化目标得到进一步的改善。 论文实验基于开源多目标优化算法程序库MOEAFramework[29]实现。硬件配置:Intel(R) Core(TM) i5-2430M处理器、4 GB RAM、Windows 8(64位)操作系统。 以AFSCN标准数据集进行实验,该数据集包含7个独立的实验场景,统计信息如表1所示。 表1 AFSCN数据集Table 1 Datasets of AFSCN 此外,需要说明的是:① AFSCN数据集并未给出卫星信息,论文假定卫星数量与任务数量一致,且在规划周期内每颗卫星的任务需求为1次;② 场景S1~S7中,地面站数量为9个,天线数量为19个;③ AFSCN数据集规定了任务转换时间,具体为:低轨任务的转换时间为20 min,高轨任务转换时间为15 min;④ 任务最低持续时间设置:低轨卫星任务最低持续时间等于可见时间窗口的持续时间,高轨卫星任务最低持续时间等于任务要求的持续时间。 为了验证论文提出的基于领域知识的启发式策略的有效性,选择无偏好的NSGA-II、SMS-EMOA、R2-EMOA这3种MOEA为本体,嵌入基于领域知识的启发式策略构建了NSGA-II-H、SMS-EMOA-H、R2-EMOA-H算法用于解决卫星地面站资源规划问题。将NSGA-II-H、SMS-EMOA-H、R2-EMOA-H的规划结果与相同参数设置下的NSGA-II、SMS-EMOA、R2-EMOA的规划结果进行比较。NSGA-II-H、SMS-EMOA-H、R2-EMOA-H的参数设置:种群规模100;交叉概率0.7;变异概率0.01;任务扩充系数2。在S1~S7实验场景,使用NSGA-II-H、SMS-EMOA-H、R2-EMOA-H、NSGA-II、SMS-EMOA、R2-EMOA各独立运行30次,每次运行10 min(M×Υs,其中M代表任务数量,Υ代表优化目标函数维度,计算得S1~S7平均运行时间约为10 min)。随机抽取运行结果进行比较,比较结果如图6所示。 在图6中,横坐标代表任务规划失败率,纵坐标代表天线的负载平衡度。NSGA-II-H、SMS-EMOA-H、R2-EMOA-H均使用了基于领域知识的启发式策略,而NSGA-II、SMS-EMOA、R2-EMOA未使用该策略,对比发现NSGA-II、SMS-EMOA、R2-EMOA在S1~S7实验场景中任务规划失败率均高于0.1;在相同的任务规划失败率条件下,NSGA-II-H、SMS-EMOA-H、R2-EMOA-H在负载平衡度这一优化目标上优于相应的NSGA-II、SMS-EMOA、R2-EMOA,即NSGA-II-H、SMS-EMOA-H、R2-EMOA-H能够获得质量更高的解;NSGA-II-H、SMS-EMOA-H、R2-EMOA-H在所有实验场景下均拓展了任务规划失败率在0.1%以下的部分,即能够在兼顾天线负载平衡度的情况下规划更多的任务,这对于卫星管理部门非常重要(相比于天线负载平衡度,卫星管理部门更加偏重对任务规划失败率的关注);NSGA-II、SMS-EMOA、R2-EMOA虽然在任务规划失败率0.25以上仍然找到了部分解,但如此高的任务规划失败率对于卫星管理部门而言往往不易接受。 图6 基于领域知识的启发式策略实验分析Fig.6 Experimental analysis of heuristic strategies based on domain-knowledge 在图7中,选择S4实验场景对上述算法的收敛性做了进一步分析,其中横坐标表示个体评估次数,纵坐标表示世代距离[30](Generational Distance, GD),世代距离的值越小表明算法的收敛性越好,即 (17) 式中:Γ表示待评估解集;PFref表示参考Pareto前沿;d(x,PFref)表示Γ中解个体距PFref的最小欧氏距离。 由图7可知,在10 min的运行时间内NSGA-II-H、SMS-EMOA-H、NSGA-II、SMS-EMOA均已收敛,R2-EMOA-H及R2-EMOA未收敛,这是由于R2指标的计算较为耗时,导致在10 min的运行时间内算法对解空间的搜索不足;NSGA-II、SMS-EMOA、R2-EMOA在世代距离这一指标上均劣于相应的NSGA-II-H、SMS-EMOA-H、R2-EMOA-H;NSGA-II-H、SMS-EMOA-H、R2-EMOA-H在迭代初期与末期的世代距离变化范围在0.015之内,这表明论文提出的基于领域知识的启发式策略能够将算法对解空间的搜索范围约束到具有优质解的解空间之内,从而提高了算法的搜索效率。 图7 S4实验场景下算法的收敛性分析Fig.7 Convergence analysis of algorithms in S4 scenario 在图8中,选择S6实验场景对基于领域知识的启发式策略中的负载平衡策略进行了有效性分析,其中“无负载平衡”指在任务扩充阶段和任务缩减阶段均采取随机处理方式。实验结果表明,负载平衡策略可以有效提高解的质量,这是因为在任务扩充阶段,负载平衡策略能够产生负载平衡度相对较好的初始潜在任务执行时间窗口集合;在任务缩减阶段,负载平衡策略在缩减任务数量过程中总是缩减工作时长最长的天线所对应的任务,这使得负载平衡程度得到进一步改善。综上所述,论文提出的基于领域知识的启发式策略的有效性得到验证。 图8 负载平衡策略实验分析Fig.8 Experimental analysis of load-balance strategy 将论文提出的基于领域知识的启发式策略嵌入T-NSGA-II、T-SMS-EMOA、T-R2-EMOA这3种偏好MOEA算法中,构建了T-NSGA-II-H、T-SMS-EMOA-H、T-R2-EMOA-H算法用于解决卫星地面站资源规划问题。为了说明上述偏好算法在求解问题上的针对性和优化性,选择两组算法进行实验比较:一是基于领域知识的启发式策略构建的无偏好NSGA-II-H、SMS-EMOA-H、R2-EMOA-H算法;二是基于文献[20]提出的卫星地面站资源规划多目标优化算法框架构建的NSGA-II-MA、SMS-EMOA-MA、R2-EMOA-MA算法(“MA”代表“Memetic Algorithm”)。在算法的参数设置上,考虑到偏好MOEA只关注偏好相关的解,因此不需要求出全部解集,故种群规模设置为15,其他参数与NSGA-II-H、SMS-EMOA-H、R2-EMOA-H设置一致。 在参考点的选择上,通常可以根据历史规划方案的统计值以及应用场景进行设置。论文模拟设置了(0.01,0.3)、(0.05,0.25)以及(0.1,0.2)3组 参考点用于引导算法的搜索进程,其中(0.01, 0.3)的参考点更注重任务规划失败率这一优化目标;(0.1,0.2)的参考点更注重负载平衡度这一优化目标;(0.05,0.25)的参考点代表二者的折衷偏好。在S1、S4、S7场景中使用参考点(0.01,0.3),S2、S5场景使用参考点(0.05,0.25), S3、S6场景中使用参考点(0.1,0.2),实验结果如图9所示。 由图9可知,T-NSGA-II-H、T-SMS-EMOA-H、T-R2-EMOA-H在S1~S7实验场景下,均能找到参考点附近的解,即能够提供决策者偏好的规划方案,提升了问题求解的针对性;与未引入偏好信息的NSGA-II-H、SMS-EMOA-H、R2-EMOA-H以及NSGA-II-MA、SMS-EMOA-MA、R2-EMOA-MA相比,基于偏好的T-NSGA-II-H、T-SMS-EMOA-H、T-R2-EMOA-H在多数场景下能够找到决策者偏好的质量更好的解,这体现了偏好算法在求解卫星地面站资源规划问题上的优化性。在相同的运行时间内(10 min),以R2-EMOA构建的R2-EMOA-MA算法在S1~S7实验场景下均未收敛,这是因为R2指标的计算比较耗时;R2-EMOA-H基本收敛,这表明论文提出的基于领域知识的启发式策略的求解效率高于文献[20]的局部搜索策略;T-R2-EMOA-H完全收敛,这说明偏好算法具有更高的求解效率。 图9 偏好MOEA算法实验分析Fig.9 Experimental analysis of preference-based MOEA 为了客观地评价各算法的性能,选择IGD-CF[31]指标对算法进行比较,该指标以参考集中距离参考点最近的解为中点定义一个ROI,并在此ROI中计算经典的IGD[32](Inverted Generational Distance)指标,即 (18) 式中:PROI表示算法落入ROI内部的解集;PFROI表示ROI内部的参考解集;d(x,PROI)表示PFROI中解个体距PROI的最小欧氏距离。 由于卫星地面站资源规划问题的参考集未知,故独立运行T-NSGA-II-H、T-SMS-EMOA-H、T-R2-EMOA-H、NSGA-II-H、SMS-EMOA-H、R2-EMOA-H、NSGA-II-MA、SMS-EMOA-MA、R2-EMOA-MA各10次,每次运行10 min,以算法生成的所有非支配解构建一个复合参考集用于IGD-CF指标的计算。论文中设定的ROI定义为边长0.1的矩形,针对上述各算法分别独立运行30次,每次运行10 min,各算法的IGD-CF指标统计结果如表2所示。 表2中IGD-CF指标的描述方式为“a(b)”,其中“a”代表30次运行结果的中位值,“b”代表标准差,“—”代表无效值(算法运行结果未落入ROI,导致计算IGD-CF指标的中位值或者标准差时数值为无穷大)。对比各算法的IGD-CF指标可知,偏好算法T-NSGA-II-H、T-SMS-EMOA-H、T-R2-EMOA-H在该指标上优于无偏好的NSGA-II-H、SMS-EMOA-H、R2-EMOA-H及NSGA-II-MA、SMS-EMOA-MA、R2-EMOA-MA算法,即偏好算法生成的解在ROI内具有更好的收敛性和分布性,且3种偏好算法在性能上差别不大;NSGA-II-H、SMS-EMOA-H、R2-EMOA-H算法在该指标上优于相应的NSGA-II-MA、SMS-EMOA-MA、R2-EMOA-MA算法,这表明论文提出的基于领域知识的启发式策略与文献[20]相比具有一定的优势;比较T-R2-EMOA-H、R2-EMOA-H、R2-EMOA-MA这3种基于R2-EMOA构建的算法在IGD-CF指标上的性能可知,T-R2-EMOA-H完全收敛且性能与T-NSGA-II-H、T-SMS-EMOA-H相当,R2-EMOA-H在该指标上的数值约为T-R2-EMOA-H的2倍,R2-EMOA-MA在多数场景下生成的解未能收敛至ROI导致其IGD-CF指标为无效值,这更进一步地说明了论文提出的基于领域知识的启发式策略的有效性和基于该启发式策略构建的偏好算法的优化性。 表2 IGD-CF指标性能分析Table 2 Performance analysis of IGD-CF 1) 论文提出的基于领域知识的启发式策略与偏好MOEA算法相结合能够有效提升地面站资源规划问题求解的针对性。 2) 基于领域知识的启发式策略构建的偏好MOEA算法与无偏好算法相比,在解的优化性上有一定的提升。 3) 与现有算法相比,论文提出的算法更符合地面站资源规划问题的现实需求,能够根据决策者指定的偏好信息更有针对性地求解问题,有很好的应用前景。2 算法设计
2.1 算法框架
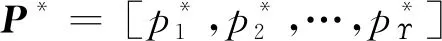
2.2 编码策略、交叉算子及变异算子
2.3 基于领域知识的启发式策略
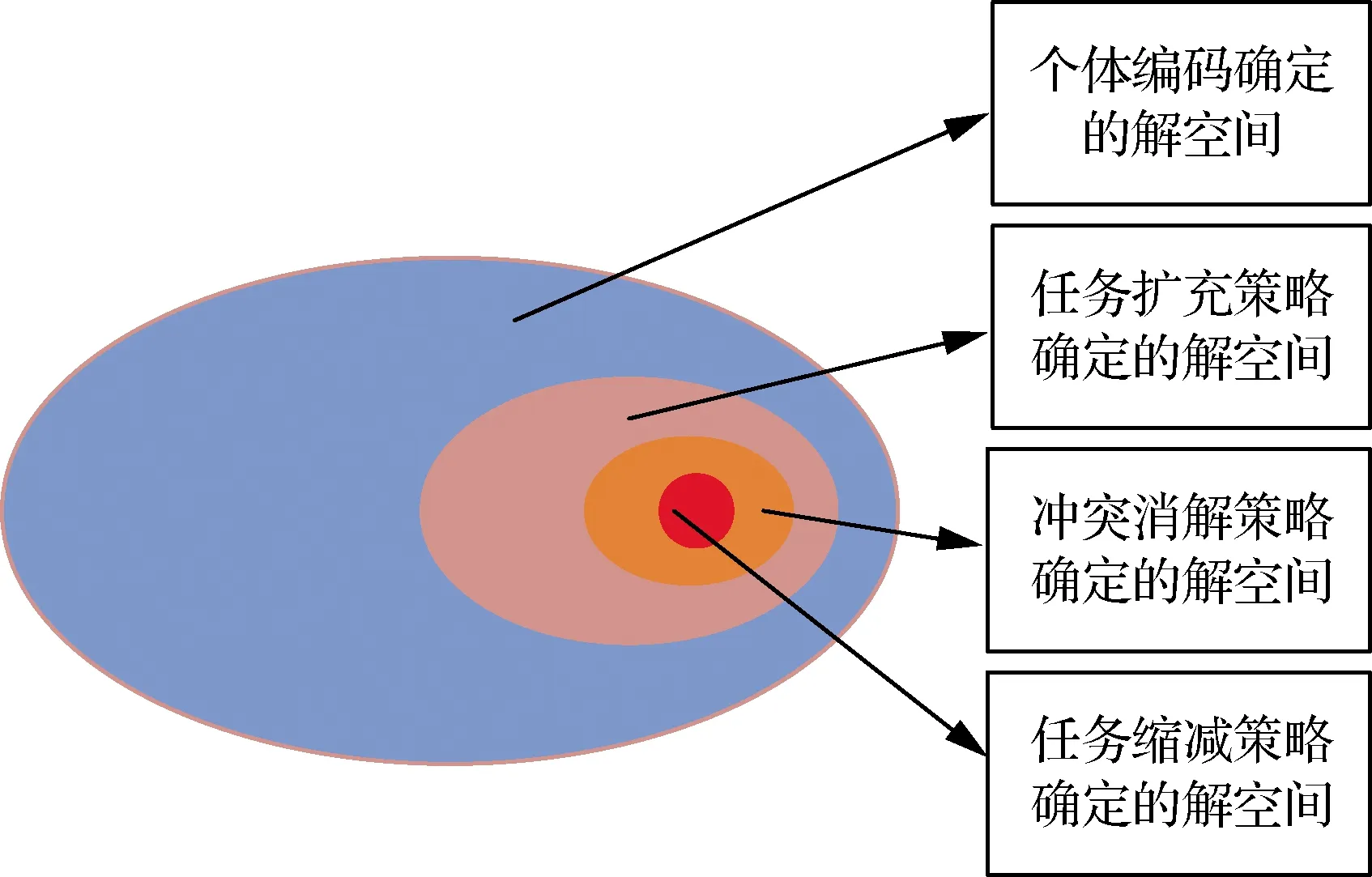
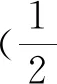
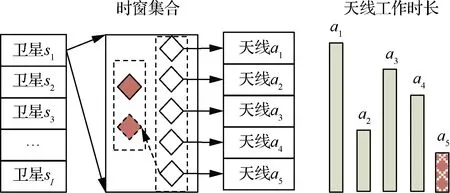


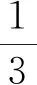

3 实验研究
3.1 实验场景
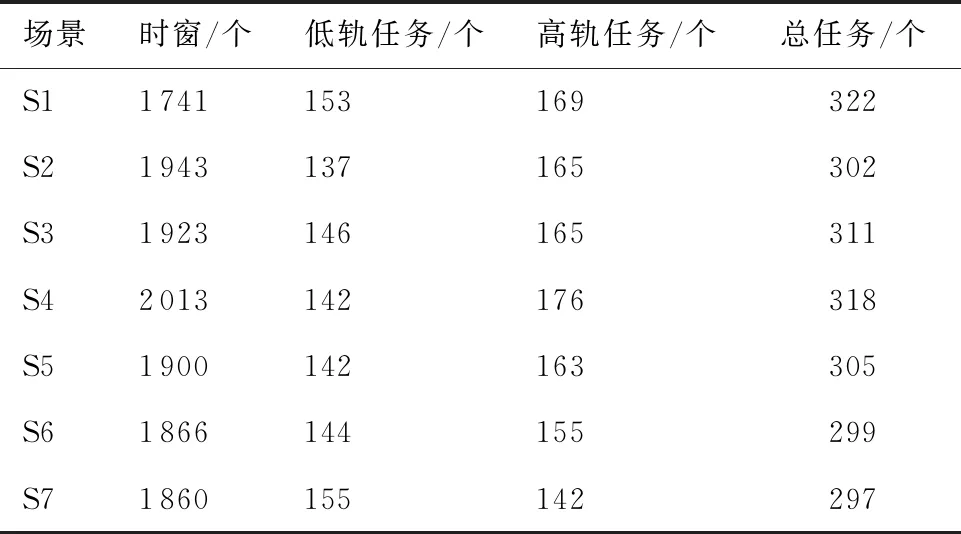
3.2 基于领域知识的启发式策略实验分析
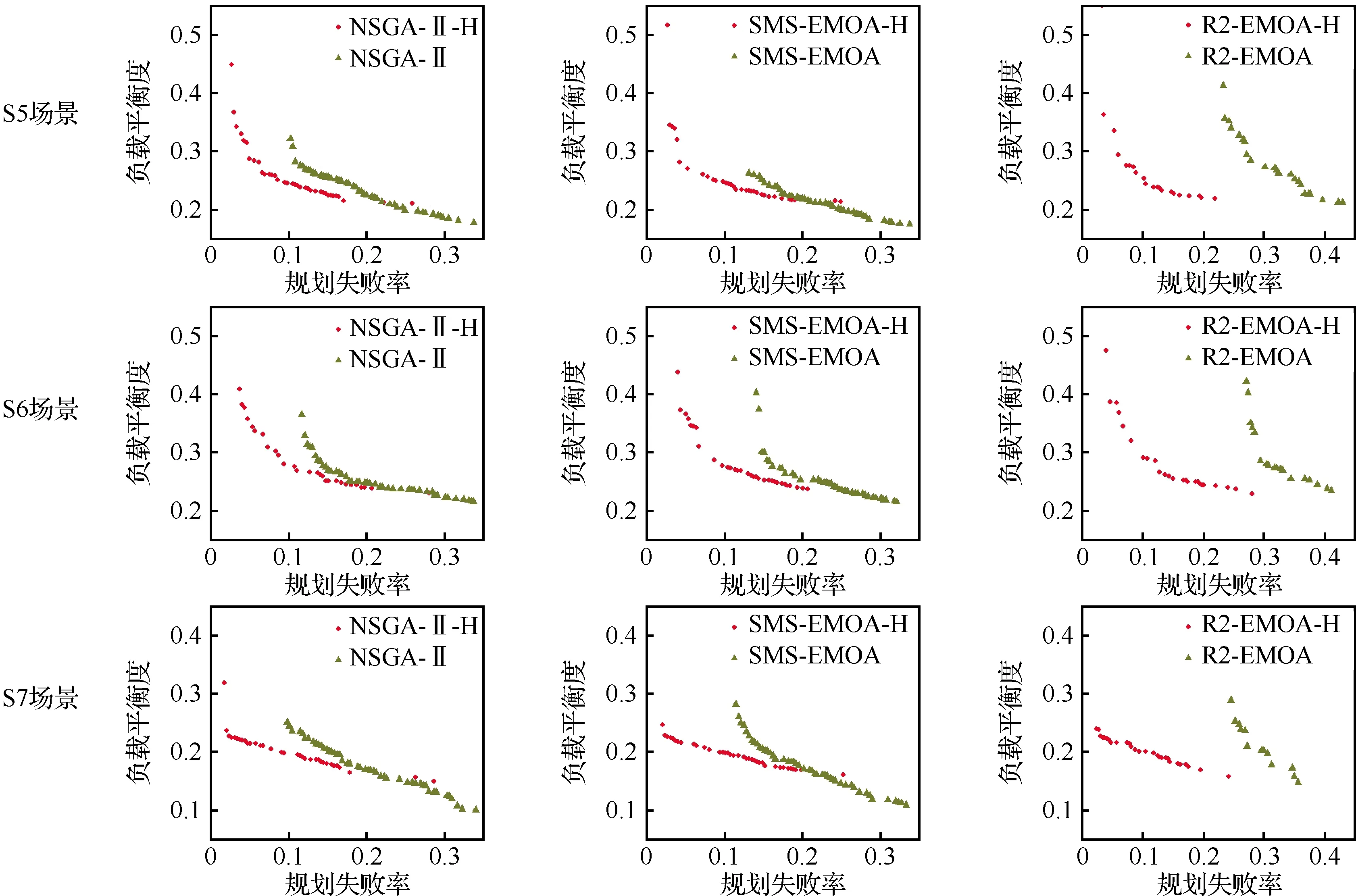


3.3 偏好MOEA实验分析

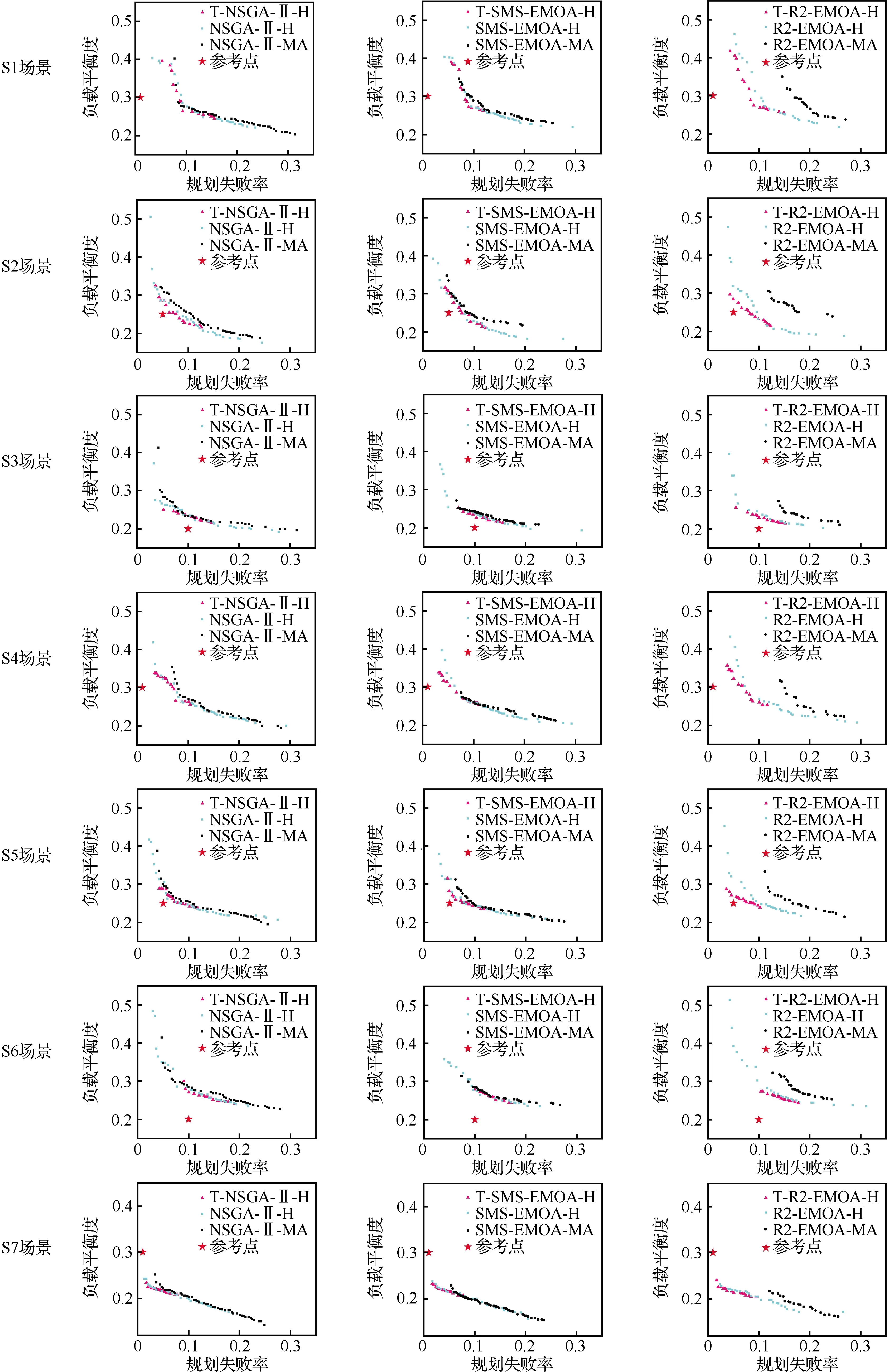
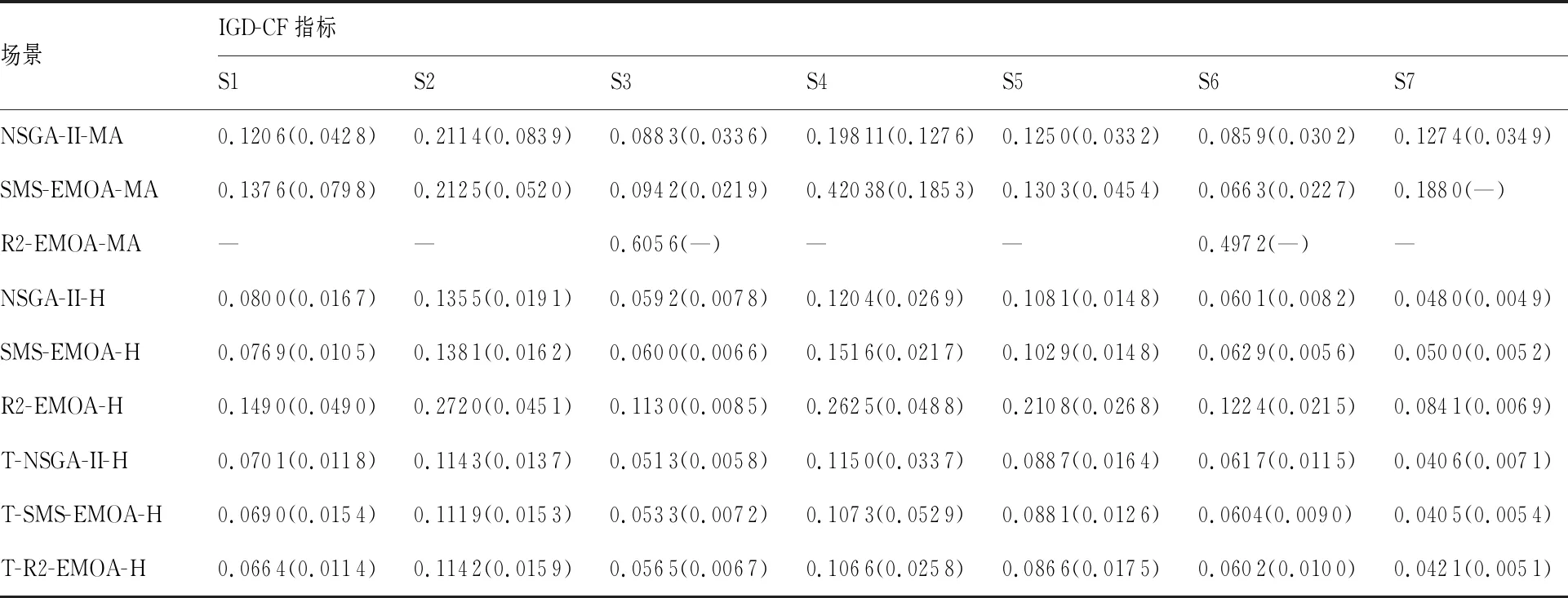
4 结 论
