闭孔泡沫铝压缩力学性能的实验和三维有限元模拟

戴开达， 吴东旭， 张志成， 陈鹏万

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

泡沫金属具有低密度、良好的力学性能、隔热、吸声等特点，在轻质结构、能量吸收领域有广泛的应用前景[1].目前，国内外已有很多研究小组对泡沫金属的压缩性能和吸能机理进行了深入的研究[2-7].研究表明，泡沫金属细观结构的随机性对其压缩力学特性有影响[8].由于泡沫金属的复杂且不规则的微观结构，难以准确描述其力学性能.早期较系统的研究是GIBSON等[1]所做的一系列工作,他们在单一孔单元的基础上建立了立方体胞元模型.先后发展出14面体[9]及8面体模型等[10].但是单胞元模型的单元形状与规则排列的特点过于理想化，与泡沫金属实际的结构不相符.ZHANG等[11]使用Voronoi拓扑算法建立泡沫金属的三维随机模型.此外，还有应用算法随机分布孔洞，建立起来的三维随机椭球体模型[12]和三维随机多面体模型[13].但是，这些模型的结构受算法的随机因子影响较大.

近年来，逐渐有学者提出了建立基于泡沫金属结构的三维真实有限元模型.ZHU等[14]和JEON等[15]通过使用同步辐射X射线显微断层照相技术并进行一系列图像处理、划分网格，获得了泡沫金属的三维真实有限元模型，该方法最大程度地还原了泡沫金属的孔洞形态.但是试件尺寸越大，重建步骤越为复杂，且无法稳定控制部分网格质量.李侯贞强等[16]通过CT扫描试件，将扫描得到的灰度图像上的像素点映射到空间坐标系中并一个点生成一个6面体单元，避免了图像重建过程中网格质量难以控制的问题.由于计算能力的限制，采取间隔取点，以减少生成的单元数量.但若构建大尺寸的三维模型，则生成的单元数量过于庞大.闭孔泡沫铝的胞壁粗细不一，若间隔取点将使较细的孔壁被遗漏，人为地造成模型上的缺陷.而在闭孔泡沫铝的有限元力学分析中，结构上的缺陷会导致应力集中，对于模拟结果的真实性产生影响.

ANDREWS等[17-18]研究发现压缩试件的截面边长大小与孔径大小之比大于7时,才能避免由于边界效应引起的测量其力学特性的误差.MUKAI等[19]发现当试件的截面尺寸大于6 mm时，才能避免重复试验始终得到不同的结果.由于闭孔泡沫铝的平均孔径约为1～4 mm，试验时往往需要制备大尺寸的试件.为了对大尺寸的闭孔泡沫铝试件进行数值模拟，本文提出了一种反映闭孔泡沫铝真实结构的三维有限元模型建模方法.此方法能够在一定程度上保证计算精度，同时又提高计算效率.基于建立的三维有限元模型进行数值模拟，并结合实验进行闭孔泡沫铝的准静态和动态压缩力学行为的研究，分析闭孔泡沫铝的准静态和动态压缩应力-应变曲线和变形特性.

1 实验试件和装置

1.1 实验材料和试件

实验中使用的闭孔泡沫铝基体材料是铝合金6061(由昆山福而顺电子科技有限公司提供闭孔泡沫铝板材，铝合金成分包含铝、铜、镁、硅等)，密度为2.75 g/cm3.采用电火花线切割成若干个Φ20 mm×30 mm和Φ20 mm×10 mm的试件，如图1所示.其中，尺寸Φ20 mm×30 mm的试件(见图1(a))用于进行准静态压缩试验，Φ20 mm×10 mm的试件(见图1(b))用于进行动态压缩试验.动态压缩试件尺寸参考文献[5，20]，2篇文献中试件的尺寸分别是13 mm×13 mm×10 mm与Φ30 mm×10 mm.通过称重法测得闭孔泡沫铝的密度为0.467 g/cm3，相应的孔隙率为83.0%.

图1 实验样品图Fig.1 Photographs of specimens

1.2实验装置

材料试验机被用于开展准静态压缩试验.通过压头上的力传感器得到其压缩力，压缩进行到试件应力-应变曲线出现显著上升时停止.应力通过载荷除以圆柱试件的横截面积得到.压缩时试件在长度方向上的形变量与原长之比为应变.为保证数据精度，每组试件测试2次.

采用直径37.5 mm LC4铝合金杆的分离式霍普金森压杆(SHPB)设备进行动态压缩试验.图2为SHPB装置图，主要由空气枪、子弹、入射杆、透射杆、吸收杆、吸收装置、动态应变仪、示波器等部分组成.子弹长400 mm，入射杆和透射杆长度均为1 500 mm.试件夹在入射杆和透射杆之间.实验中在入射杆及透射杆上粘贴应变片，采用电阻应变片用来测量记录入射波、反射波和透射波.采用三波法得到闭孔泡沫铝材料的动态压缩应力、应变等数据.

图2 SHPB装置示意图Fig.2 Scheme of SHPB

采用中国科学院高能物理研究所的225 kV X射线显微CT设备进行扫描.在保证扫描精度的情况下，为了方便处理后期数据，选用20～35 μm的扫描精度.通过360°旋转试件得到不同角度的扫描数据，对这些数据进行滤波、校正等处理，得到dicom格式的灰度图像.

2 有限元模型的重建

2.1 材料阈值的划分方法

CT扫描闭孔泡沫铝试件得到的图像是由铝基体和空气组成的.二者的X射线衰减值有明显差别.CT值的单位是Hounsfield，简称为Hu，范围是-1024～3071.CT值与衰减值成正相关[21].而灰度值是CT值的映射，范围是0～4096.所以铝基体和空气的灰度值同样相差极大，如图3.

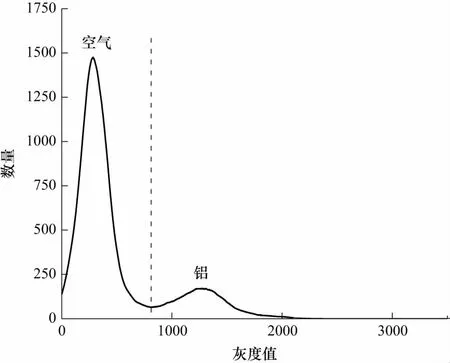
图3 灰度值矩阵中灰度值-数量曲线Fig.3 Gray value-quantity curve in gray value matrix

因此，可以采用“单一全局阈值法”划分铝基体与空气的灰度值.将灰度值划分为2个集合G1和G2.其中，G1中的灰度值大于初始阈值T0，G2中的灰度值不大于初始阈值T0.获取集合G1和G2中灰度值的数量，分别记为n1和n2.分别计算集合G1和G2中所有灰度值的加权平均值u1和u2

(1)

式中：x为灰度值；y为值为x的灰度值的数量.

(2)

根据加权平均值u1和u2更新阈值T.判断更新后的阈值T与初始阈值T0之间的差值绝对值是否小于设定的迭代截止参数ΔT，若小于，则更新后的阈值T为最终的设定阈值.使用更新后的阈值T重新对灰度值进行划分，然后重复上述步骤，直到差值绝对值是否小于设定的迭代截止参数ΔT.

计算得到阈值T为815.对灰度值矩阵进行阈值分割，筛选得到所有属性为铝基体的像素点.

2.2 三维有限元模型的重建方法

建立三维有限元模型的步骤如下：以Φ20 mm×30 mm圆柱形试件为例，CT扫描得到灰度图像，同时顺次为各灰度图像编号.其中，灰度图像各像素点的属性为铝基体或空气.使用软件Matlab中dicomread函数读取灰度图像得到灰度值矩阵.其中，灰度值矩阵的序号与灰度图像的编号一一对应.同时，灰度值矩阵的灰度值与灰度图像的像素点一一对应.

通过划分阈值的方法筛选出所有铝基体的像素点.根据像素点在图像中的位置，得到其三维空间中的位置点坐标.将试件所在的三维空间均匀划分为多个相同大小的立方体区域.根据铝基体位置点与立方体中心点的距离，筛选出与铝基体位置点距离最近的所有立方体区域即模型的单元.

可以适当调整立方体区域的边长大小(增大边长，得到的单元越少)，满足运算效率需求.由于每一个铝基体位置点都有一个对应的立方体区域，在改变边长大小后不会造成缺陷，能够在一定程度上保证计算精度.

图4为生成得到的三维真实有限元模型，模型共有292 355个单元及491 158个节点，孔隙率为81.9%.灰度图像和三维有限元模型不同截面的孔隙率误差较小，如图5所示.任取泡沫铝的一个截面上的灰度图像(图5(a))与三维模型截面(图5(b))的孔隙率相差为-1.2%，另一个截面上的灰度图像(图5(c))与三维模型截面(图5(d))的孔隙率相差为-1.6%.

图4 三维有限元模型Fig.4 Three-dimensional finite element model

图5 灰度图像和相应的模型截面图Fig.5 Grayscale images and cross-sections of 3D model

3 实验及计算结果分析

3.1 闭孔泡沫铝的准静态力学特性

通过材料试验机对Φ20 mm×30 mm的闭孔泡沫铝试件进行准静态压缩试验.同时，采用有限元软件ANSYS/LSDYNA对闭孔泡沫铝试件的准静态压缩试验进行数值模拟，不考虑空气影响.图6为闭孔泡沫铝的准静态压缩试验的数值分析模型.

图6 准静态压缩数值分析模型Fig.6 Numerical analysis model under quasi-static compression

模拟计算中闭孔泡沫铝基体材料为铝合金6061.其本构选取塑性随动模型(*MAT_PLASTIC_KINEMATIC模型).各项参数如下：杨氏模量为75 GPa，泊松比为0.3，密度为2.75 g/cm3，屈服强度为170 MPa.试验机压头材料为45号钢，在数值模拟中以加载板替代压头的作用.假设加载板为刚体，本构关系可用刚体模型( *MAT_RIGID模型).加载板的参数如下：杨氏模量为210 GPa，泊松比为0.3，密度为7.85 g/cm3，支撑板与加载板材料一致.刚性加载板以恒定速率v=1.8 mm/min向下加载，对支撑板的垂直方向进行约束.采用自动的面对面接触，并设置刚性板与试件端面之间的摩擦系数为0.1.采用最大主应变破坏准则.设一个单元上最大主应变大于0.3时，材料失效破坏，删去单元.

图7为闭孔泡沫铝准静态压缩试验与模拟得到的应力-应变曲线.闭孔泡沫铝压缩变形可分弹性变形阶段、屈服平台阶段、密实变形阶段3个阶段.

弹性变形阶段：应变较小的弹性阶段，整个试件均匀变形，应力-应变曲线呈线弹性，弹性应变在0.010～0.025之间.

屈服平台阶段：当应力继续增大超过弹性极限时，变形进入塑性阶段.由于闭孔泡沫铝孔洞呈多面体形状，孔壁上存在各种缺陷(孔壁褶皱、孔壁缺失及薄弱孔壁)，使其孔壁结构受力不均匀，导致应力集中.试件局部产生塑性变形.应力变化平缓，但应变变化范围比较大，出现了一个屈服平台.该阶段是闭孔泡沫铝吸收能量的主要阶段，应变范围在0.025～0.750之间.

密实变形阶段：闭孔泡沫铝的应变大于0.750.随着孔洞被压实，应力突然急剧增大，相应的应力-应变曲线上应力快速上升.该阶段属于致密化阶段，闭孔泡沫铝的能量吸收能力大大降低.

如图7所示，弹性变形阶段内应力-应变曲线近似为一条斜直线，应力达到最高点时，材料发生初始屈服，当应力继续增大时，曲线进入屈服平台阶段.文中将应力-应变曲线中第1个应力峰值作为闭孔泡沫铝的屈服强度.若没有明显的峰值，取应变0.05时相应的应力为材料的屈服强度[22-23].从应力-应变曲线得到实验与模拟中的闭孔泡沫铝的屈服强度分别为7.55 MPa和7.39 MPa，相对误差为-2.12%，模拟与实验结果吻合较好.实际压缩试验进行到一定程度，闭孔泡沫铝材料失效破坏，发生断裂.小部分材料从试件上脱落，使最后得到的应变增大.

图7 准静态压缩下试件的应力-应变曲线Fig.7 Stress-strain curve of specimen under quasi-static compression

图8为试件模型上某一截面(经过轴心)准静态压缩下的应变云图.当试件应变ε=0.1时，变形进入塑性阶段.由于闭孔泡沫铝孔壁结构受力不均匀，导致应力集中.局部产生塑性变形如图8(a)所示，主要是孔壁屈曲.塑性变形的分布主要沿着加载轴约45°方向，这与文献[24]的结论一致.局部发生塑性变形导致应力释放，应力-应变曲线上(见图7)应力在达到塑性屈服点后会突然下降.当ε=0.2时，更多的孔壁发生塑性变形，如图8(b)所示，引发邻近孔的应力集中，形成变形带.此时应力释放，对应应力-应变曲线上第2个应力谷底.当ε=0.3时，变形带基本被压实，如图8(c)所示.变形带硬化，引起应力上升现象.当ε=0.5时，变形带周围的孔洞上应力集中，孔洞坍塌、孔壁断裂.变形带向周围扩展逐渐形成一个更大的变形区域(见图8(d)).变形带的坍塌引起一次次应力波动，使应力-应变曲线上屈服平台阶段呈锯齿形(见图7).此时，试件截面被压缩成类梯形.

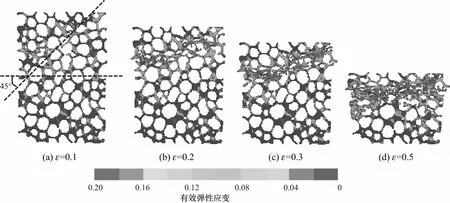
图8 准静态压缩下的应变云图Fig.8 Strain contour plots under quasi-static compression

3.2 闭孔泡沫铝的动态力学特性

图9为Φ20 mm×10 mm闭孔泡沫铝试件的动态压缩试验的数值分析模型.子弹以初速度v0(8～21 m/s)撞击入射杆，试件受压变形.改变子弹初速度，得到不同应变率下的模拟结果.假设子弹、铝合金杆与闭孔泡沫铝试件的材料参数基本相同，本构选取为*MAT_PLASTIC_KINEMATIC模型，材料参数与准静态模拟相同.其它接触、失效准则也一致，并采用自由边界条件.采用Cowper-Symonds模型描述闭孔泡沫铝基体材料的应变率效应

图9 动态压缩数值分析模型Fig.9 Numerical analysis model under dynamic compression

(3)

由图10可得，σy为实验得到的闭孔泡沫铝的屈服强度，σy′为模拟得到的闭孔泡沫铝的屈服强度，见表1.δ为实验与模拟结果的相对误差.其最大相对误差为+5.63%，且模拟曲线与实验曲线趋势一致.因此，模拟与实验结果吻合较好.动态下的闭孔泡沫铝的屈服强度和准静态(应变率10-3s-1)时相比，应变率700 s-1时的屈服强度增加不明显.但随着应变率的提高，闭孔泡沫铝的屈服强度逐渐增大.结果表明，闭孔泡沫铝的屈服强度具有应变率效应.

图10 动态压缩试验与模拟的应力-应变曲线Fig.10 Stress-strain curve of test and simulation under dynamic compression

表1 实验和模拟得到的闭孔泡沫铝的屈服强度

由于厚度10 mm的试件，沿轴向仅有2～3个孔洞.其变形模式受随机性结构影响显著.本文直接利用图6建立的准静态试验的数值分析模型对Φ20 mm×30 mm的试件进行动态压缩试验数值模拟.提高刚性加载板的下压速率，v提高到8.4，21，60 m/s(相应的应变率为280，700，2 000 s-1).图11～图12为计算得到的试件模型某一截面(经过轴心)的动态压缩下的Mises应力分布.应力最大值为试件在不同应变率下的动态屈服强度，根据式(3)计算可得.加载板下压速率为8.4 m/s时，闭孔泡沫铝试件受到压缩后25 μs时刻，图11(c)显示截面中央几处结构薄弱处出现应力集中，此时应变达到0.007.

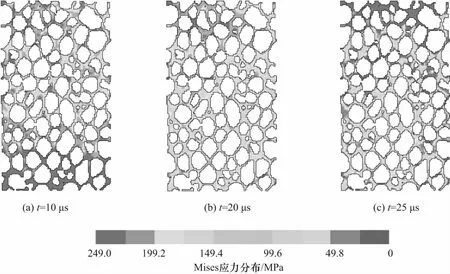
图11 子弹速度8.4 m/s时试件的Mises应力分布Fig.11 Mises stress distribution of specimen at bullet velocity of 8.4 m/s

加载板下压速率提高到21 m/s时，闭孔泡沫铝试件受到压缩后15 μs时刻，图12(b)显示截面加载端出现应力集中，试件上开始产生塑性变形，此时应变达到0.01.

图12 子弹速度21 m/s时试件的Mises应力分布Fig.12 Mises stress distribution of specimen at bullet velocity of 21 m/s

动态压缩应力-应变曲线也可分为弹性变形阶段、屈服平台阶段及密实变形阶段3个阶段，如图13所示.在应变0～0.03之间，曲线呈线弹性，应力随应变逐渐增大直至弹性极限.随着应力继续上升达到塑性屈服点，材料产生塑性变形.在应变0.03～0.60之间，从应力-应变曲线可以看出一个明显的平台区.密实变形阶段，试件上应力急剧上升.动态压缩下的闭孔泡沫铝的屈服强度远高于准静态(应变率10-3s-1)时的.随着应变率的提高(应变率为280，700 s-1，闭孔泡沫铝的屈服强度分别为14.11，14.20 MPa)，闭孔泡沫铝的屈服强度变化不明显.应变率继续升高至2 000 s-1，屈服强度达到14.96 MPa，略微提高.

图13 压缩模拟的应力-应变曲线Fig.13 Stress-strain curve of simulation under compression

厚度30 mm的闭孔泡沫铝试件的动态屈服强度明显高于厚度10 mm的闭孔泡沫铝试件，且应变率越低，差距越明显.由于厚度10 mm的试件的孔径与厚度尺寸之比过大，制备时极易形成严重缺陷.且试件部分沿轴向仅有2～3个孔洞，缺陷对试件整体压缩变形的影响显著.压缩变形时试件的某一处缺陷上迅速形成应力集中，使材料达到塑性屈服.应变率越大，局部应力集中越不明显.

4 结 论

本文提出了一种反映闭孔泡沫铝真实结构的三维有限元模型建模方法，能够更方便地对大尺寸的闭孔泡沫铝试件进行数值模拟.此方法可以适当调整立方体区域的边长大小，提高运算效率.由于每一个铝基体位置点都有一个对应的立方体区域即单元，在改变边长大小后不会造成缺陷，能够在一定程度上保证计算精度.模拟得到的应力-应变曲线与实验结果吻合较好.基于建立的三维有限元模型并结合试验进行闭孔泡沫铝的准静态和动态压缩力学行为的研究，分析了闭孔泡沫铝的压缩变形特性和力学性能.

根据数值模拟结果可以看出，动态压缩下的屈服强度远高于准静态压缩下的.准静态压缩载荷下，圆柱形闭孔泡沫铝试件主要的变形特征是沿轴线45°方向出现塑性变形并发展成变形带.低速压缩时(8.4 m/s)，闭孔泡沫铝试件的压缩变形模式与准静态相同：截面上结构薄弱处首先出现应力集中，材料达到塑性屈服.而在高速压缩时(21 m/s以上)，试件加载端首先达到塑性屈服，并沿轴向支撑端逐层圧溃.闭孔泡沫铝试件动态压缩下的屈服强度远高于准静态压缩.随着应变率的提高(280 ～700 s-1)，其屈服强度变化不明显.应变率继续升高至2 000 s-1，屈服强度略微提高.