径向非均布压力分布对湿式摩擦副热机耦合影响

王立勇， 吴瑾， 李乐， 郑长松， 张金乐

(1.北京信息科技大学 现代测控技术教育部重点实验室 北京 100192； 2.北京理工大学 机械与车辆学院，北京 100081； 3.中国北方车辆研究所，北京 100072)

湿式离合器摩擦副在工作时，泵站中的工作油通过控制油道作用于活塞，活塞移动产生的压力推动摩擦副相结合，以此实现离合器的换挡作用.蔡丹等[1]通过实验发现了加载压力分布方式和摩擦副翘曲方式的关系.王立勇等[2]发现热点数目随加载压力的增加而增多，工作油压增加使得钢片表面温升增加，但是过高的油压反而使最大温升的幅值变小.陈遥飞[3]用有限元软件分析了影响离合器接触初始压力分布的因素.陈瑶等[4]模拟分析表明，局部加压方式钢片的最大应力及径向应力梯度均大于均匀加压方式.

据离合器经验表明，离合器的失效故障引起的原因中，其摩擦副接合压力不合理加载是主要的影响因素之一.以往研究通常只分析加载压力大小随时间及变化路径的变化过程，对其在空间的径向变化分析较少，即非均布的压力对摩擦副损伤研究较少.湿式摩擦副的工作过程是热机耦合物理过程，应力空间分布的非均匀性势必会影响温度场的空间分布状态，进而影响高温带的峰值及其空间分布特征，故在文章中采用有限元模拟的方法分析不同形式的空间非均布压力作用下摩擦副温度场、应力应变场的变过过程，探讨径向非均布力对摩擦副损伤产生及发展的影响规律.

1 理论分析

1.1 热传导模型

在摩擦副工作过程中，摩擦表面的温度会随时间发生变化，以热传导和热对流为主，其热辐射很小，对偶钢片二维轴对称非稳态热传导方程为

(1)

式中：λi为导热系数；ρi为密度；ci为比热容；Ti为摩擦元件的温度；t为工作时间；x，y为摩擦副某点坐标；i取值1，2分别为钢片和摩擦片.

1.2 摩擦生热

湿式摩擦副接触面单位时间产生的摩擦热，即某点瞬时输入的热流密度为

q(x,y,z,t)=μ(Δω)pi(x,y,z,t)Δωr

(2)

式中：q为单位面积某点热流密度；μ为摩擦因数；pi为该点的接触压力；Δω为摩擦副的相对转速差；r为该点距摩擦副中心的半径.

热量在两者之间进行分配，分配系数式Kq为

(3)

式中:λs、ρs、cs分别为对偶钢片导热系数、密度和热容量；λf、ρf、cf分别为摩擦片的导热系数、密度和热容量.

2 摩擦副有限元模型

摩擦副有限元模型如图1所示.考虑湿式离合器的工作过程中，油液多次循环冷却，设定初始环境温度设置为20 ℃.

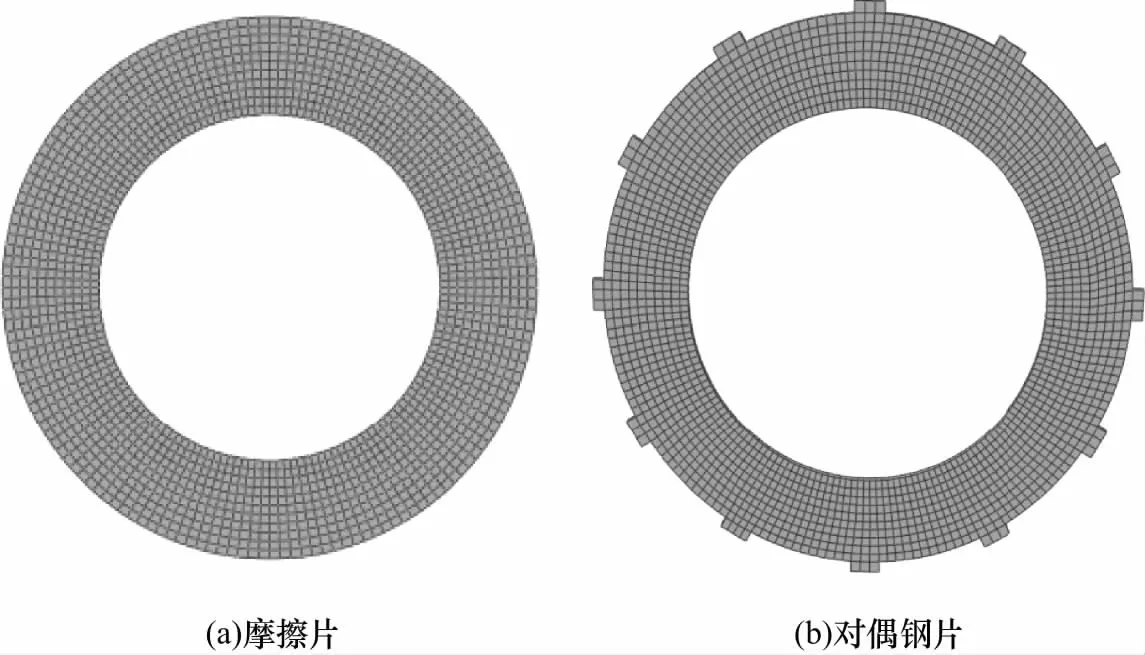
图1 摩擦副有限元模型Fig.1 Friction pair finite element model

2.1 对流换热

对偶钢片与摩擦片中心对称面因两边载荷对称而各取一半结构的对称面，所以外界没有热交换，满足绝热边界条件[5].假设摩擦副内外侧圆环表面与空气对流换热，取经验参考值5～25 W/(m2·℃)[6].湿式摩擦副间有润滑油流过，忽略润滑油的热传导及摩擦副吸收的热量，摩擦副接触面与润滑油液接触存在对流换热，则表达式为[7]

(4)

式中：Pr为普朗特系数；Nu为传质努塞尔数；m1为摩擦副盘面温度沿径向分布的指数，假设其为线性分布，则m1=1.

关于摩擦副的内外侧圆环面的对流换热可认为冷却油横掠圆柱体：

(5)

式中:v(i,o)为内外环面线速度；d(i,o)为内外环面直径；m2，n为经验系数，依照参考文献分别取0.193，0.618[8].

2.2 机械载荷

关于非均布压力的产生的原因：①非均布压力的产生跟钢片的热变形有很大关系，摩擦副在高速高温工况下，由于摩擦副在工作过程中摩擦生热，摩擦副盘面吸收热量会发生热应力变形，产生非均匀接触，进而使得加载压力分布不均匀，为不可控因素；②摩擦副的压力分布与结构设计也息息相关，比如在活塞外径处开泄压孔，调整钢片内齿的几何参数、调整钢片的碟形度、数量和硬度值，采用不同结构形式的散热沟槽等，在一定程度上可控[9-16].

文中作者给出了5种不同的压力分布，旨在尝试分析径向非均匀的压力分布对摩擦副的影响，由于摩擦副的实际接触状态复杂多变，并且无法实际测量，因此5种压力跟实际中的哪种情况对应很难一一解释清楚，论文只是简化给出了5种假想的径向非均布压力分布情况，尝试进行分析.图2(b)～(e)中压力最大值为2 MPa，边缘处为0 MPa.

图2 加载压力示意图Fig.2 Loading Pressure Diagram

2.3 径向非均布压力设置

单位网格采用三维离散一次性非协调减缩积分单元C3D8RT划分网格，摩擦片网格单元数3 572，对偶钢片单元数3 736，将摩擦副模型进行均匀合理划分.文章中有限元模型选用圆柱坐标系，通过在load模块下，Pressure的分布方式expression filed中，设置不同的表达式来达到压力在盘面径向非均布的分布.

2.4 摩擦副尺寸及材料属性

本文研究对象湿式摩擦副的摩擦片由65 Mn芯板和粉末冶金工艺制造的铜镀层组成，对偶钢片材料为65 Mn钢.在仿真模型设置中，假设湿式摩擦副的材料各项同性.钢片和摩擦片的内径分别为85 mm和80 mm，外径和模型厚度均为125 mm，0.003 mm.

表1 摩擦副材料属性参数

3 均布模拟结果分析与实验验证

3.1 有限元建模

图3为5种压力的增长速率曲线，模型运行0.15 s，时长较短，针对的是离合器工作初期快速升压阶段的油压变化[9].为便于与后期实验工况对比，图4摩擦副相对转速增长曲线是在模型中设置离合器钢片制动，摩擦片相对钢片由静止逐渐加速，相对转速由0逐渐增大.

图3 模型压力增长速率曲线Fig.3 Model pressure growth rate curve

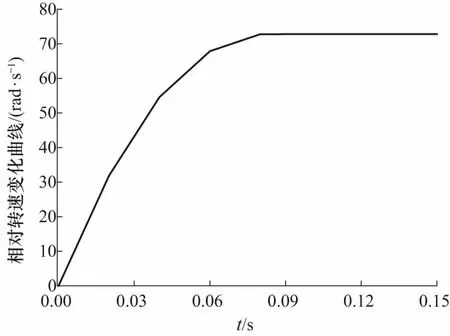
图4 模型相对转速变化曲线Fig.4 Finite element simulation relative speed change curve

3.2 均布压力模拟结果分析

图5所示为压力均匀加载情况下，在工作终态的钢片各物理量云图.

由图5的模拟结果可知，盘面的温度、应力、轴向应变的物理量最大值空间分布盘面的环带中央位置，在径向存在较大梯度.在工作过程中假设活塞推动压力是以均匀分布形式作用，摩擦接触面间的温度、应力和应变场最终均呈现非均布状态，且径向分布不均匀.由图6～7可知，钢片接触面温度场随时间的推移而逐渐增大，在0.15 s时达到最大值.工作初期高温区出现在外圆，随着时间的推移，高温带逐渐内移，在半径R=109 mm处附近温度值最大，钢片中部出现环形高温带，温度较高，盘面边缘温度较小.主要因为在湿式摩擦副工作过程中(见图4)摩擦副相对转速上升到700 r/min后保持不变，滑动摩擦产生的大量热量，钢片持续吸热，中部吸收热量来不及扩散，温升较快；盘面边缘部分由于与空气及润滑油存在对流换热，温升较慢，而且热量扩散快，温升较低.

图5 工作完成时对偶钢片接触表面各物理量云图Fig.5 Shows the physical quantity of the contact surface of the pair of steel sheets when the joint is completed

图6 钢片各节点温度随时间变化图Fig.6 Temperature change diagram of each node of steel sheet with time

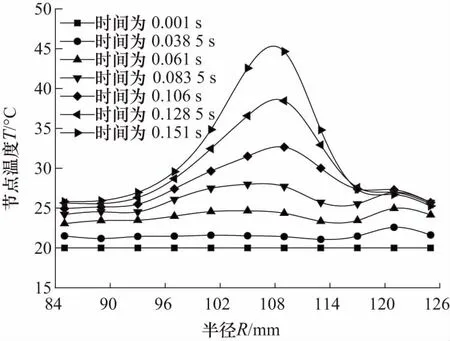
图7 钢片各节点温度随半径分布图Fig.7 Distribution of temperature with radius of each node of steel sheet

3.3 均布压力温度场实验及分析

图8为实验的温度传感器的布置，在钢片齿槽内布置传感器，安装半径分别为90 mm、98 mm、106 mm、114 mm.湿式离合器工况如图9所示.

图8 温度布置方案示意图Fig.8 Temperature sensor layout diagram

图9 湿式离合器工况介绍图Fig.9 Working condition of wet clutch

文中研究的是手动电液换挡变速箱，为更方便的研究摩擦界面温度分布规律，离合器安装单片摩擦片即两个摩擦副，其余空间均用对偶钢片填充，试验所用电机具体型号为1PH8186-1HD40-2AA1-Z，额定功率85 kW，转速范围0～4 000 r/min.在实验过程中，湿式换挡离合器输出端为抱死制动状态，将惯量装置调整到被测离合器包箱输出端，与刹车制动装置组成负载系统.图10为湿式摩擦副在工况为转速差500 r/min，接合压力0.5 MPa，润滑流量1 L/min的湿式摩擦副相对位置的温升实验结果.

图10 实验钢片盘面温度分布Fig.10 Temperature distribution of experimental steel disk

由图10和图6可知，钢片盘面温度随时间增大而增长；钢片环面径向半径较小的内侧边缘温度较低，随时间缓慢增长；在图11中，有限元模型和实验终态径向温度对比中基本一致，盘面温度差明显，内侧环面温度较低，换面中心略向外侧温度最高，为高温带.用以3.3节的离合器摩擦副均布温度场实验验证均布压力图2(a)有限元模型温度场结果，证明摩擦副模型边界条件设置的合理性.其余另外4种径向非均布压力的模型设置只是单纯修改径向压力的分布方式.

图11 模型与实验终态温度分布对比Fig.11 Temperature distribution between model and experiment

4 径向非均布压力分布对摩擦副温度场影响研究

如图12(a)～(e)所示为在均布压力、沿内径到外径线性增加、沿内径至外径线性减小、压力峰值在两侧和峰值在中心，对偶钢片在工作终态的温度云图.

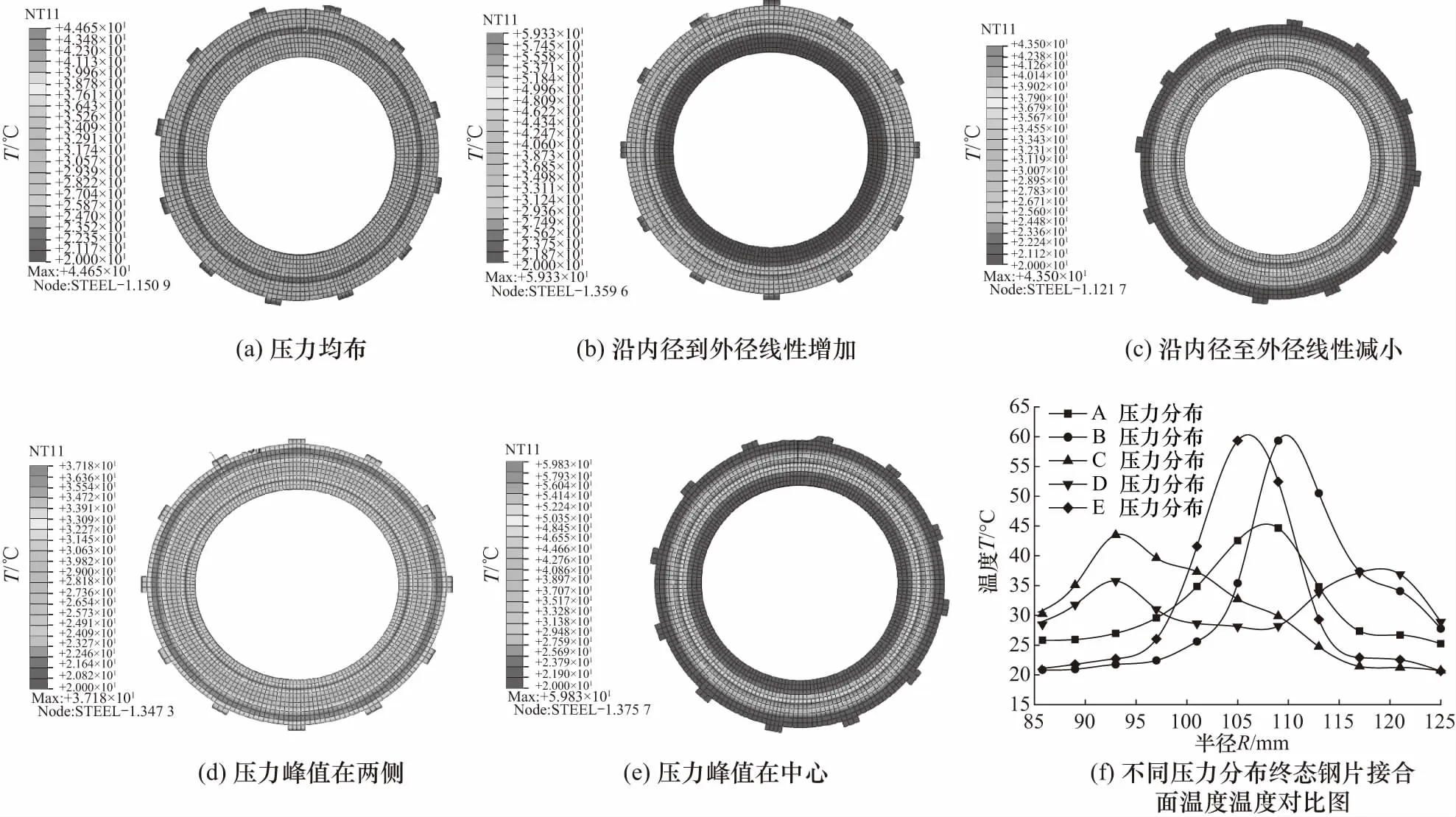
图12 不同压力分布工作终态钢片接合面温度分布Fig.12 Temperature distribution of the joint surface of the joint steel sheet under different pressure distributions

由图12(a)～(f)可知，湿式摩擦副在不同加载径向压力分布作用下，对摩擦副最大温度值和高温带分布的位置都有影响.由于在工作过程中，热流密度产生的热量值的大小与位置和盘面对流换热的作用的影响，高温环带的位置较对应压力分布峰值的位置有向盘面中心移动的趋势.

盘面最高温排序：(E)>(B)>(A)>(C)>(D)；温差：(E)>(B)>(A)>(C)>(D)；盘面最大温度增加率：(E)>(B)>(A)>(C)>(D).由表2和图12所示可知，加载压力分布状态的变化对钢片高温带的分布和温度数值有着显著的影响，D(峰值在两侧)的压力分布方式能够降低盘面的最高温度，整个盘面温度较低且温差值小.E(峰值在中心)非均布压力加载方式盘面温度最值最高且盘面温度增加率最大，盘面压力集中在盘面径向R=105 mm区域，温度值的急剧增长，盘面两侧与中心环带温差较大.B(沿内径到外径线性增长)和A(均布压力)的压力加载方式会得到高温环带位置在R=109 mm处.对比5种压力分布方式，压力的分布方式可以影响高温环带的径向位置，最高可达盘面半径的30%.

表2 不同压力分布下最高温度对比

5 径向非均布压力分布对摩擦副应力场影响研究

由图13(a)～(f)可知，湿式摩擦副在受到不同加载压力分布作用下，对摩擦副最大应力值和应力带分布的位置都有一定的影响.盘面的应力环带位置和最大应力值在外界机械加载油压和工作产生的热量被盘面吸收引起的热应力的作用下，发生改变，可以明显看出应力环带位置较原加载压力峰值位置向盘面中心方向移动.

最大Mises应力排序：(C)>(E)>(B)>(A)>(D).由表3和图13所示可知，加载压力分布状态的变化对钢片应力带的分布位置和应力最值有显著的影响.对于D(峰值在两侧)压力分布，应力值相比较其他分布方式数值最小，在工作过程中，外界机械载荷集中在盘面的边缘两侧，热量集中且对流换热较大，热应力作用相对减弱.C(沿内径至外径线性减小)最大应力最高且应力差值最大.

图13 不同压力分布工作终态钢片接合面应力分布云图Fig.13 Mises stress distribution cloud diagram of jointed steel disk joint surface under different pressure distributions

表3 不同压力分布下最大应力对比

6 径向非均布压力分布对摩擦副轴向应变场影响研究

6.1 工作终态钢片应变场分布结果分析

本文中应变是指钢片单在位长度上的变形量，在于分析载荷分布对摩擦副小变形的影响，变形是影响接触面积和摩擦力的重要因素，应变则是离合器损伤判别和可靠性设计的重要依据.由图14(a)～(f)可知，湿式摩擦副在受到不同径向压力分布的作用下，对摩擦副的应变场分布和最大应变值有一定的影响，可以明显看出应变环带位置较原加载压力峰值位置向盘面中心方向移动.摩擦副的应变场分布位置和最大应变值的大小与外界机械非均布压力分布方式和压力数值大小及摩擦生热被盘面吸收产生的热应力有关.

图14 不同压力分布工作终态钢片接合面轴向应变分布云图Fig.14 Axial strain distribution cloud diagram of jointed steel disk joint surface under different pressure distributions

最大轴向应变排序：(E)>(B)>(A)>(C)>(D).由表4所示可知，径向加载压力分布对钢片轴向应变带分布位置和应变最值有显著的影响.D(峰值在两侧)的压力加载方式应变值较小且径向梯度较小，E(峰值在中心)外界机械应力和滑摩热量集中，使此处热应力较大，以至轴向应变沿轴向增长较大.

表4 不同压力分布下最大轴向应变对比

7 结 论

在工作过程中，温度、应力和应变场环带的径向位置和各物理量的最值较原加载压力峰值位置向盘面中心方向移动，径向非均布压力的分布方式可使环带位置变化率可达到盘面宽度的10%～40%.在工作终态时，径向压力分布方式对于摩擦副的温度，应力和应变的最值有直接关系，5种径向压力分布方式相比，盘面温度最值排序：(E)>(B)>(A)>(C)>(D)；Mises应力最值排序：(C)>(E)>(B)>(A)>(D)；轴向应变最值排序：(E)>(B)>(A)>(C)>(D)；E(2 MPa压力沿内外半径波峰式分布)温度、应变最值最大；C(2 MPa压力由内径至外径线性减小)应力最值最大，D(2 MPa压力沿内径向外径波谷式)则是温度、应力和应变最小值.