激光散斑漂移现象的理论模型与成像实验
2021-07-04郭又溪贺韵博刘荣臻宫殿锦丰夏成杰
郭又溪,贺韵博,刘荣臻,宫殿锦丰,夏成杰
(华东师范大学 物理与电子科学学院,上海 200241)
自1960年激光问世以来,由于其高亮度、高方向和高相干等特性,是很多基础物理与工程问题研究的重要工具[1].本文研究的激光散斑及其漂移现象,就是一种典型的激光相干现象.激光被随机粗糙介质散射后,会在空间中形成颗粒状图样,被称作激光散斑[2];当光源、散射介质彼此相对移动的时候,会观察到散斑的漂移.直接观察低功率激光笔照射在粗糙表面上的光斑,并轻微晃动头部,就可以观察到这一现象.激光散斑及其漂移现象具有广泛应用,比如测量材质表面的粗糙程度[3, 4],探测物体的微小位移或形变[5],测量不稳定流场的速度分布等[6,7].
激光散斑是被随机散射的激光在空间中相干,进而在成像系统中观察到的随机图样.当成像系统相对于静止的光场移动时,图案自然也发生移动.利用如图1所示的实验装置便可观察到此现象.这些现象原则上可以利用波动光学的基本原理进行计算[8],但具体的计算方法和步骤并不简单.此外,波动光学给出的计算结果不直观,无法清晰解释观察到的像到底是“哪里的像”,以及散斑漂移的“快慢”如何依赖于焦距等成像系统几何参数等问题.对这一现象更基础和直观的理论解释、以及完整的建模算法,可以帮助人们加深对这一常见的激光散射现象的认知,促进在相关定量测量方面的创新应用.

图1 实验装置示意图(用CCD相机拍摄经激光照射的粗糙表面,在电脑中观察散斑图像.当相机平移时,散斑图像相应移动)
本文从波动光学与几何光学两个角度来分析激光散斑及其漂移现象,并开展成像实验,所得理论结果均与实验相符.在第1节,我们首先简述关于激光散斑出现机制的正态散斑模型.在此模型的基础上,我们基于波动光学原理数值计算散斑图案,并模拟当成像系统移动时散斑的漂移过程.随后,我们介绍等价的几何光学理论.在第2节,我们介绍观察激光散斑漂移的实验装置,以及定量分析其漂移量的图像处理算法.在第3节,我们展示实验结果,并对比实验、数值计算,以及几何光学理论的结果.总结与讨论在第四节中.
1 散斑及其漂移现象的理论模型
1.1 正态散斑模型
正态散斑模型是描述激光散斑现象的简化模型.散射屏平面受线偏振、单色、平行相干光的照射,出射光场的复振幅可表示为
U0(ξ,η)=A0(ξ,η)exp[iφ0(ξ,η)]
其中(ξ,η)表示散射屏上的平面直角坐标,实数标量场A0(ξ,η)和φ0(ξ,η)分别表示振幅与相位.模型假设出射光场具有以下统计性质[9,10]:1)不同空间位置的A0和φ0是随机数,且两者无关;2)它们各自的数学期望与方差和空间位置无关;3)空间中任意两点的数值的相关性为0;4)A0的平均值为1,即散射屏平均透射率为常数且归一化为1;5)φ0为均匀分布在[-π,π)之间的随机数.此外,在散射屏上,假设只有一直径为D的圆形区域被激光照亮,即激光光束的有效直径.
在上述假设下,计算沿散射屏法向传播距离z后的光强分布,及其空间自相关函数,得到单个散斑的光强分布在横向(垂直于光传播方向)和纵向(平行于光传播方向)的平均半峰宽分别为[9]:1.22λ/D和8λz2/D2,其中λ为激光波长.一般而言,激光光束直径D为毫米量级,而成像平面与散射屏的距离z为米量级,所以散斑具有空间各向异性,其横向大小远小于纵向大小,可形象地理解为一个个长轴沿光传播方向的旋转椭球,如图2.
由上述分析可知,若纵向移动观察设备,成像平面上的散斑不断消失和出现,观察到散斑的“闪烁”现象;而横向移动观察设备可观察到散斑的漂移现象(图2).并且,由于散斑形状的各向异性,相对于横向移动,需纵向移动成像设备较大一段距离后,才能观察到明显的光场变化.在本文的理论及实验研究中,我们只分析横向移动成像设备时所观察到的散斑漂移现象,但介绍的数值计算方法也可简单地推广到向任意方向移动成像设备的情形中.

图2 单个激光散斑的横纵向尺寸以及成像平面移动示意图
1.2 傅里叶光学计算激光散斑成像
正态散斑模型给出了散射屏平面上的光场复振幅,由此出发可近似计算平行于散射屏的任意平面上的光场复振幅,包括在传播过程中经过透镜的情况.在傅里叶光学中,相干光复振幅在空间中的传播,其数学形式类似于对传播前的复振幅的空间分布进行二维傅里叶变换;而(薄)透镜的作用可近似为改变了复振幅的相位的空间分布.
基于惠更斯-菲涅尔原理,在菲涅尔近似下,散射屏平面的光场U0(ξ,η)传播至z平面处的复振幅为[8]
(1)
其中k=2π/λ为波数,Σ表示积分区域,即整个散射屏平面.对比二维傅里叶变换公式,上式简写作
(2)
其中F {·}表示做二维傅里叶变换.由式(1)中exp[-ik/z(xξ+yη)]一项可知,傅里叶变换后所得二维频谱图中各点的频率坐标(fξ,fη)与z平面处光场的实空间坐标(x,y)存在如下对应关系
x=λfξz,y=λfηz
(3)
将式(2)与其复共轭相乘,可以得到z处光强分布.
如光路中存在透镜,则在式(1)、(2)中令z=zt,得到紧贴透镜前方的平面上的光场复振幅Ut(xt,yt),其中(xt,yt)表示透镜所在平面的直角坐标,zt为透镜与散射屏之间的距离.紧贴透镜后方的平面上的光场复振幅为
(4)
其中
(5)
表示透镜的相位变换因子,其中f是透镜的焦距[8].
经过透镜后,光场再次传播一段距离W后的光场可通过与式(2)相同的方式进行计算,得到成像平面上的复振幅为

(6)
1.3 散斑及其漂移的数值计算
上述公式给出了计算经过或不经过透镜时、不同位置的成像平面上的光场的方法.如果不经过透镜,成像平面上的图样被称作客观散斑,对应于实验上用不加装镜头的CCD直接成像,得到成像平面处客观存在的光强分布[11].如经过透镜,观察到的图样被称作主观散斑,它取决于透镜的焦距、对焦距离等成像参数[9].基于式(1)—(6),我们可以编程计算并展示客观与主观散斑的图样.数值计算的基本流程见图3.
1) 散射屏表面复振幅.在正态散斑模型的基础上继续简化,我们将散射屏表面的光场复振幅表示为一个直径为D的圆形区域(即光斑),其内部各点的复振幅的幅值为1,相位为均匀分布在[-π,π)之间的随机数,光斑之外各点的复振幅为0.在程序中可用如下方法进行离散化近似.
首先,生成一个N行N列的方形矩阵,规定矩阵中心为坐标原点,且矩阵对应的实际空间在x与y方向的范围均为[-L0,L0].所以,用该矩阵表示的光场,其空间分辨率为2L0/N,而矩阵第n行m列的元素对应的空间坐标为
(ξ,η)=[(2n/N-1)L0,(2m/N-1)L0]
将此矩阵的各元素设为相位随机均匀分布,且模长为1的复数.随后,再生成一个新的、大小相同的矩阵表示激光光斑所在区域,即满足
[(2n/N-1)L0]2+[(2m/N-1)L0]2 的第n行m列的元素被设为1,其余为0.将这两个矩阵的元素对应相乘,(矩阵元素对应相乘的含义指:相乘后所得矩阵的第n行m列的元素,等于两个矩阵各自第n行m列的元素的乘积),得到矩阵U0[n,m],对应于散射屏表面的出射光场U0(ξ,η),如图3(a)所示. 图3 数值计算过程中各平面上的光场矩阵以及数值计算流程示意图((a)散射屏表面光场复振幅的实部;(b、c)紧贴透镜前方(b)和后方(c)的平面上的光强矩阵It与It′;(d)成像平面上的光强矩阵;(e)沿光轴从左到右为数值计算中依次计算的各平面上的光场) 2) 沿散射屏法向传播距离z后的复振幅.生成一个与U0矩阵大小相同的相位矩阵,该矩阵第n行m列的元素的数值为 (7) 对应于式(2)中的exp[ik(ξ2+η2)/2z].随后,将此相位矩阵与U0[n,m]的元素对应相乘,再对相乘后的矩阵进行离散傅里叶变换,得到二维频谱矩阵.在计算机算法中,通常利用快速傅里叶变换(FFT)算法完成离散傅里叶变换;在我们实际使用的Matlab语言中,还需利用fftshift命令,将零频率对应的元素调整到矩阵中心. 根据Nyquist采样定理,对于离散的图像U0[n,m],其傅里叶变换后的二维频谱图的频率范围是:[-N/4L0,N/4L0].所以,根据式(3)可写出频谱矩阵对应的实空间坐标(x,y)的范围均为 (8) 再生成一个新的相位矩阵表示式(2)中的 依据图1表征的信息可以大致发现,若蚂蚁A(组团A)至少完成一段(全程或局部)有效反馈行为——正反馈过程,对蚂蚁巢穴具有积极的正相关作用;若蚂蚁(组团)无法完成一段有效反馈行为——负反馈过程,对整个蚁群而言属于内耗亏损行为过程,增加整个蚁群定靶食物源难度[5]. 该矩阵第n行m列的元素的数值为 (9) 将此相位矩阵与频谱矩阵的元素对应相乘,得到空间中距离散射屏z处的光场的复振幅矩阵. 3) 客观散斑光强分布及其漂移.将上述复振幅矩阵与其复共轭矩阵的元素对应相乘,便得到光场沿散射屏平面法向传播距离z之后的光强分布(图3(b)),即该平面上的客观散斑.如果将成像平面放置于此,所得到的散斑图样便是该矩阵所表示的图像.显然,当成像平面在垂直于平面法向的方向上移动距离ΔXobs时,观察到的散斑的移动距离ΔXspeckle与成像平面的移动距离等大反向,即:ΔXspeckle=-ΔXobs.为方便起见,下文所有移动距离均用其绝对值表示,即忽略由于运动相对性所带来的负号. 4) 透镜前后光场复振幅.在得到上述客观散斑的光场复振幅的基础上,继续计算存在透镜时观察到的主观散斑的图样.首先,同样利用式(7)~(9)计算紧贴透镜前方的平面上的复振幅矩阵Ut[n,m],计算过程中空间平面与散射屏的距离z应替换为散射屏与成像系统透镜的距离zt.随后,生成与Ut矩阵大小相同的透镜相位变换矩阵t[n,m],该矩阵中各矩阵元素的数值为 (10) 5) 主观散斑光强分布及其漂移.最后,计算透镜后方距透镜W处的成像平面上的光场.计算方法与计算沿散射屏法向传播距离z后的复振幅的方法相同,只需将U0[n,m]替换为Ut′[n,m],将传播距离z替换为像距W.将得到的复振幅矩阵与其复共轭矩阵的元素对应相乘,得到在成像平面处的光强分布矩阵.如图3(d)所示,可以看到图像中存在一个明显的光斑,其内部有颗粒状图案,即主观散斑.这对应于实验上利用加装透镜的成像系统观察到的图样. 为数值计算主观散斑的漂移,可从Ut[n,m]中取出两个大小为N′ 在傅里叶光学的描述中,透镜改变了光场相位的空间分布,从而影响光场的传播.在几何光学的描述中,透镜使光线发生弯折,产生汇聚或发散,使距透镜前方V处平面上的像被聚焦在透镜后方W处的平面上,其中V和W被称作物距和像距,它们之间满足高斯公式 (11) 首先,我们认为在数值计算(图3(d))与实际实验(图5(c),(d))的结果中出现的光斑,是散射屏上的激光光斑经透镜在成像平面上所成的像;而光斑中的散斑,则是垂直于光轴的某平面上的相干光场的像.当成像系统移动时,光斑和散斑的像也同时移动,移动大小可通过如下方式计算. 1) 光斑(spot)的漂移.如图4所示,光轴经过散射屏中心、透镜中心、成像平面中心.当成像系统(透镜与成像平面)沿垂直于光轴的方向移动ΔXobs距离后,散射屏中心与新的透镜中心所在的直线,与成像平面交于新的一点,该点相对于成像平面中心的移动距离为ΔXspot.利用简单的几何关系可以得到 (12) 我们定义光斑移动距离与成像系统移动距离之比(即上式等号左边)为光斑移动速率.注意Z并不一定等于此时像距W所对应的物距V,即此时激光光斑所成的像是失焦的. 图4 主观散斑成像的几何关系示意图(从左到右各竖直平面依次为:散射屏,对焦面(物距为V的平面),透镜所在平面,成像平面(像距为W的平面).水平虚线表示成像系统移动前后的光轴,两条倾斜虚线连接了(i)成像系统移动之前,散射屏或对焦面上过光轴的点,与(ii)成像系统移动之后,这两个点在成像平面上所成的像的位置.箭头ΔXobs与ΔXspot(ΔXspeckle)分别表示成像系统移动的距离与散射屏(对焦面)上一固定点的像相对于成像系统移动的距离) 2) 散斑(speckle)的漂移.由透镜的基本成像原理可知,成像平面上所成的散斑图样,正是物距V平面上的光强分布.利用与上文类似的几何关系可以得到,当成像系统沿垂直于光轴的方向移动ΔXobs距离后,散斑相对于成像平面的移动距离ΔXspeckle满足 (13) 类似的,ΔXspeckle/ΔXobs被称作散斑移动速率.由式(13)、(14)可知:在V≠Z时,光斑的漂移速率不等于散斑的漂移速率,即二者会发生相对移动. 在数值计算及下文的实验结果中发现,当V>Z,即透镜对焦在散射屏后方实际并不存在光场的位置时,依旧可以观察到散斑,且其漂移速率的确满足式(13).这一“悖论”可以通过惠更斯原理理解.若散射屏处的光场向后传播,也可在后方的平面上形成光场.这一后方光场再向前传播,在成像平面上成像,与散射屏处的光场直接向前传播所成的像一致,这正是透镜对焦于散射屏后方时观察到的像.上述“悖论”源于几何光学本身的局限性,但也体现出几何光学在成像问题中与波动光学的分析结果是自洽的. 利用几何光学还可以讨论物距和镜头光圈大小对成像的影响.当V=Z时,所成的像即是散射屏上光斑的像,具有清晰的边界.而当物距过大或过小时,则出现失焦,形成弥散光斑,没有清晰边界.镜头光圈决定弥散光斑的大小:光圈越大,进入镜头的远轴光线越多,光斑边界越模糊,光斑越大.同样的,光圈越大,散斑本身也越模糊. 我们利用加装与不加装镜头的CCD相机研究主观与客观散斑及其漂移现象,尤其是各成像参数(物距、光圈大小)对主观散斑漂移现象的影响.实验装置如图1所示.将一束波长为λ=480 nm的线偏振激光照射一张80目砂纸(粗糙表面).在粗糙表面前方用连接电脑的工业相机(大华A7500CU75面阵相机)进行拍摄.相机正对粗糙表面上的激光光斑中心,两者连线与粗糙表面法线方向的夹角为θ,相机成像芯片中心与激光光斑中心之间的距离为r,用(r,θ)表示相机所处的初始位置.相机被安置在精密位移台上,通过调节位移台将相机沿平行于成像平面的方向移动.实验中,每移动ΔX后,停止移动并拍摄一张图像.相机的像元尺寸为3.45×3.45 μm2,即所得图像的每个像素的宽度是3.45 μm. 在研究客观散斑的漂移时,我们将相机固定于(r,θ)=(39.5 cm,26.5°)处,取ΔX=0.25 mm,连续移动并成像20次.在研究主观散斑时,我们将相机固定于(r,θ)=(44.0 cm,26.5°)处,并加装一焦距为f=35 mm的定焦镜头,通过调节镜头的对焦环,在不同的物距V下进行实验.取ΔX=0.5 mm,连续移动及成像30次.实验现象如图5所示.在此实验中,我们固定镜头的光圈为F=2.此外,我们也固定物距V=24 cm,改变光圈为F=8与F=16(光圈F数值越大,光阑直径越小,通光量越小),重复上述实验以探究光圈大小的影响. 图5 (a、b)相机移动1 mm前后拍摄到的客观散斑图样;(c、d)相机移动0.5 mm前后拍摄到的主观散斑图样 当成像系统移动时,图案中的散斑会向相反的方向移动,即散斑漂移.通过计算移动前后两张图片的相关矩阵,可以定量计算散斑漂移的量.相关矩阵的计算方法可由相关函数的定义作离散化后推广而来.对于两个二维函数f1(x,y)、f2(x,y),其二维相关函数定义为 corrf1,f2(u,v)=∬f1(x,y)f2(x-u,y-v)dxdy (14) corrf1,f2(u,v)的最大值所在的坐标(uM,vM),代表将f2平移(uM,vM)后与f1重合度最高.所以可以利用相关函数的最大值坐标来计算散斑的漂移量:如果成像系统移动前后在不同位置拍摄的两张散斑图样经一段平移后几乎重合,那么这段平移距离就是散斑的漂移量.数学上,相关函数等价于先将其中一个函数“翻转”后再计算两个函数的卷积(*) ∬f1(x,y)f2(x-u,y-v)dxdy=corrf1,f2(u,v) (15) (16) 将上述计算离散化之后,可以高效处理矩阵图像,用以计算散斑图像的漂移量.首先,对两张图像之一进行上下、左右翻转,然后计算两张图像各自的离散傅里叶变换,得到频谱矩阵.将频谱矩阵的对应元素相乘后,再做逆变换(式(16)),即可得到两张图像的相关矩阵.相关矩阵中最大值的元素的位置对应于散斑的漂移量,可以通过矩阵的大小即图像的分辨率换算得到散斑的漂移量ΔXspeckle.在进行离散傅里叶变换时,需要将N行N列的矩阵用0填充成行2N-1列.上述利用快速傅里叶变换计算的时间复杂度为O(Nlog2N),相比于直接计算相关矩阵的时间复杂度O(N2),具有明显优势,尤其是在处理像素较多的图像时.例如,对于我们实际计算的5000×5000像素的图片,利用上述方法仅需数秒便可完成. 在主观散斑现象中,光斑也存在漂移.光斑的漂移量即两张图片中光斑的平均像素位置之差,再通过图像分辨率换算得到ΔXspot.光斑“中心”的平均像素位置可以通过计算矩阵中所有元素的坐标以其元素数值作为权重的加权平均得到. 利用上述方法,我们计算了当成像系统移动不同距离时,成像实验及数值计算中得到的客观散斑、主观散斑和光斑的漂移量.对于实验数据,我们根据所用的CCD的像素尺寸(1像素=3.45 μm),将图像中散斑和光斑的漂移量的单位由像素换算为毫米.对于数值计算的数据,也根据图像的空间分辨率进行了相应的换算.结果表明,(主、客观)散斑与光斑的漂移量都正比于成像系统移动的距离(图6).我们用过原点的直线对这些数据进行拟合,其斜率即为散斑(或光斑)的漂移速率,即成像系统移动单位距离时散斑(或光斑)的漂移量. 图6 (a)客观散斑漂移量随相机移动距离的改变(圆圈为数据点,实线为拟合数据所得的直线,表示ΔXspeckle∝ΔXobs;(b,c)主观散斑现象中,光斑(b)与散斑(c)的漂移量随相机移动距离的改变.不同形状的数据点对应于不同的物距,(b)、(c)两图中同样形状的数据点代表相同的物距.(b)图中箭头方向表示物距V增加) 如图6(a),客观散斑的漂移速率为1.005±0.006.对于主观散斑,不同对焦距离下,散斑与光斑的漂移距离与相机移动距离的关系如图6(b),(c)所示,它们的漂移速率在图7中.当V=Z时,镜头对焦于散射屏,由于光场还未传播和相干,所以观察不到光斑内部的散斑.当V>(<)Z时,散斑的漂移速率小于(大于)光斑的漂移速率.同时,图7中还绘制了数值计算(1.3节)得到的主观散斑和光斑的漂移速率,以及根据几何光学模型(1.4节)给出的漂移速率的理论曲线(式(12)、(13)),实验数据、数值计算数据、理论计算值在误差范围内几乎完全一致. 图7 不同物距下光斑(空心符号)及主观散斑(中心带点符号)的漂移速率.数据点表示实验(圆圈)与数值计算(方块)的结果,线条表示几何光学理论的解:实线表示光斑的漂移速率,点线表示散斑的漂移速率.竖直虚线表示光斑与散斑漂移速率相等时的物距,等于实验中散射屏上激光光斑中心与CCD成像芯片中心之间的距离(r=44.0 cm) 此外,我们发现镜头光圈大小只会影响光斑的大小,而不改变光斑及散斑的漂移速率.我们也在实验上验证了,散射面的粗糙程度只影响散斑的平均大小,而对其漂移速率没有影响. 本文利用傅里叶光学的理论以及相应的数值计算方法,计算了不同像距下的客观及主观散斑的图样及其漂移过程;并利用几何光学,形象地解释了散斑漂移现象,及其与透镜成像参数的依赖关系,给出了散斑和光斑漂移速率的表达式;并且,我们搭建了实验装置,观察了散斑漂移现象,建立了一套定量计算散斑和光斑漂移量的数据分析方法.研究结果表明:客观散斑漂移速率为1,其位移大小等于成像系统的位移大小;主观散斑漂移速率依赖于对焦距离.实验、数值计算与理论结果均相符,表明了数值计算方法的正确性与几何光学模型的合理性. 基于上述研究,我们可以对激光散斑现象及其应用原理进行一些简单的讨论.利用激光散斑的漂移性质,可以间接测量散射体与成像系统的相对移动速度.我们认为,测速时应选取合适的对焦距离(散射体与成像系统之间的距离的0.2到3倍之间),过大的对焦距离使得散斑漂移速率很小,漂移现象不明显,而过小的对焦距离导致漂移速率太大,所得图像之间的相关性弱.两者都会影响根据散斑漂移速率反推移动速度的精度.另外,实验经验表明,当用人眼观察激光散斑时,散斑漂移速率总是大于光斑移动速率.说明人眼观察激光散斑时,对焦平面总是在散射屏与人眼之间,这可能是由于人眼更倾向于首先对焦在近处的物体上. 此外,实验中还发现,如果激光功率较大,粗糙表面会受热,从而膨胀、形变,即使成像系统的位置固定,也会观察到较为混乱无规的散斑热漂移现象,这与本文研究的由于相对运动所导致的散斑漂移现象原理类似,但现象不同. 综上所述,本文在理论和实验上系统性地研究了激光散斑的形成及漂移现象.我们相信,这些理论分析和计算方法,不仅能够帮助大学光学课程的教师和学生对这一经典的光学相干现象获得更直观和深入的理解,也可有助于定量分析相关工程问题中的现象,促进激光散斑原理的应用.
1.4 主观散斑漂移的几何光学模型

2 激光散斑成像实验
2.1 实验装置与研究参量

2.2 散斑漂移量的计算方法
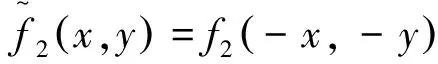
2.3 光斑漂移量的计算方法
3 实验、数值计算、理论结果


4 讨论与总结
