谐振子的经典和量子统计分布

康琳惠，张 林

(陕西师范大学 物理学与信息技术学院，陕西 西安 710119)

经典统计是描述宏观体系状态的统计理论,而量子统计则是描述微观系统统计性质的理论，两种统计方法所遵循的统计原理本质上是相同的，即都是把系统的宏观量作为相应微观状态的统计平均值.量子统计与经典统计的根本区别在于它们的动力学基础不同，经典统计是以经典动力学为基础，而量子统计则是建立在量子动力学的基础之上，这就导致对微观粒子运动的描述方式截然不同.谐振子模型作为在经典物理和量子物理中都非常重要的模型，是理解很多复杂体系行为的最基本单元.本文通过对谐振子系统的经典统计分布和量子统计分布的详细研讨，以Mathematica软件为数学辅助手段，通过可视化的图像，比较和归纳出经典统计与量子统计的区别和联系.这一比较研究可以更加深刻地理解谐振子在宏观和微观尺度下不同的统计行为，从而加深对量子力学基本规律的理解和认知.

1 经典运动和统计分布

(1)

则运动方程可写为

(2)

x(t)=Asin(ωt+φ)

(3)

(4)

对于遵循经典运动的谐振子，我们可以由其在势阱中位置的统计测量结果来获得其运动的状态.根据经典运动的解(3)，谐振子在平衡位置附近的运动被限制在-A到A之间.当我们大量测量振子的位置，会发现其位置在x到x+dx之间被测到的概率P(x)dx与振子在此区间停留的时间dt成正比

(5)

其中T是振子来回运动一次的周期，分子上的2表示振子来回过程中有两次经过同一区域.值得一提的是，在周世勋先生编写的《量子力学教程》(第二版)中的第33页线性谐振子一节中[2]，给出的经典统计概率密度为

(6)

该式子没有考虑到振子来回过程中有两次经过同一区域，因此其概率密度也会加倍，所以分子上应该乘以2.该问题虽小，但由于这个2的存在，可以非常自然地得到经典的归一化的概率分布.由式(5)有

(7)

其中v=dx/dt是振子在x到x+dx之间的运动速度.利用振子的运动方程：x(t)=Asin(ωt+φ)可以得到

(8)

将上式带入P(x)得到归一化的经典统计分布

(9)

这是一个在x=±A处有奇点的分布，运用Mathematica的积分函数Integrate[P(x),{x，-A，A}]可以非常方便地计算出P(x)的积分为1，即经典谐振子在区间[-A，A]上的经典分布自洽得满足几率之和为1.

2 量子运动和统计分布

如果把经典振子缩小到量子尺度，虽然振子所处的势场不变，但振子的运动状态将不能采用经典力学中的位置和速度(或动量)来描述，而其运动行为直接由波函数ψ(x)给出的统计性质来描述，波函数满足定态薛定谔方程：

(10)

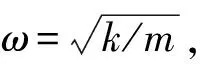
(11)

(12)

(13)

利用Mathematica程序对谐振子在经典平衡位置附近的分布进行图像展示.如图1给出了谐振子处于最低的几个能态的波函数图像，波函数的纵轴的位置是相应能级的位置.

图1 谐振子的波函数图像分布(从下到上依次为n=0基态,n=1,2,3,4的波函数图像)

由此可知，量子谐振子的波函数是坐标x(ξ≡αx)的函数，虽然它不能表示振子在某一时刻的位置坐标，但波函数绝对值的平方|ψn(ξ)|2与振子在空间某点出现的概率成正比，即它出现在某一位置的概率密度是可以确定的.一维谐振子的概率密度为

(14)

为此我们在Mathematica中做出其相应的概率密度分布如图2.

(a) n=0

(b) n=2

(c) n=15图(实线)与对应经典概率分布(虚线)比较

从图2中谐振子的经典(虚线)和量子(实线)概率密度分布可以看出：

1) 经典统计：对于经典动力学行为，在平衡位置ξ=0处，经典谐振子出现的概率最小，这是由于此时谐振子动能最大，振子在x=0处停留时间最短，测量到的概率也最小.而在两边最大值(振幅)处，振子的速度为零，停留时间较长，更容易测到振子，因而出现的概率最大.当然振子的能量越大其位置分布的范围也越大.

3 谐振子的经典和量子能量

经典谐振子的动能Ek和势能Ep的表达式为

(15)

(16)

振子的总能量E

(17)

显然在运动过程中，经典谐振子的能量是连续变化的且总能量保持不变.

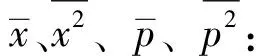
(18)

(19)

(20)

(21)

则有

(22)

(23)

可以得到

(24)

如果能量取成谐振子的量子能量，那么

(25)

此统计结果与量子谐振子给出的统计结果也完全一致[1].

4 谐振子的相空间动力学描述

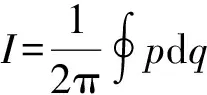
(26)

而量子力学中这个作用量是量子化的

(27)

表明其能量是量子化的.

在谐振子的相空间的描述中，经典振子的动力学状态是一个封闭的圆(标度后)，如图3(a)所示.而对应振子的量子状态在相空间的描述则比较复杂[5]，我们采用正定的Husimi函数[6]来描述振子相空间分布.对于任意数态|n〉，其相空间的Husimi分布函数为

(28)

(a) 经典粒子的相轨道(右上角是随时间的振动)

(b) n=1相空间分布(白色虚线对应能量的经典轨道)

(c) 在经典轨道上加入随机噪声后的相空间演化轨道

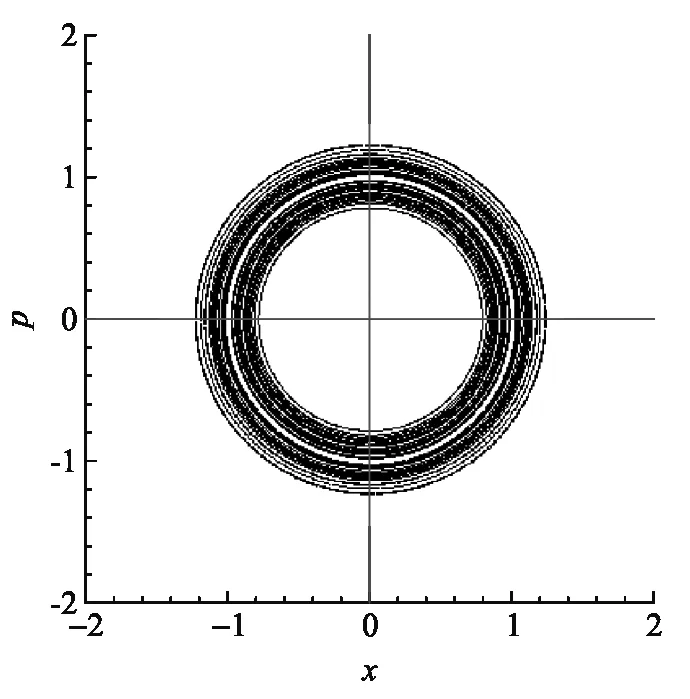
(d) 在经典轨道上(中间实线圆)加入初始动量为高斯分布的相空间轨道分布图3 谐振子的相空间动力学描述

显然对于相干态|α〉而言参数α的实部Re(α)和虚部Im(α)分别可以对应振子的位置和动量：

(29)

(30)

因此可得

(31)

(32)

数态|n〉的分布如图3(b)所示为有宽度的环(虚线则为经典的轨道)，数态的量子轨道相空间统计分布体现了量子的涨落(环的宽度)，而经典相轨道(白色虚线)则只是量子平均的结果，显然二者有本质的区别，因为量子的概率统计分布是无法用经典轨道加入随机噪声进行动力学统计来还原的.图3(c)是在经典谐振子方程中引入高斯型白噪声后多个随机动力学轨道的相空间图像，多个经典随机轨道演化后的统计分布结果显然和量子分布图3(b)不同，所以微观谐振子动力学行为不能简单用加入随机过程的经典动力学来进行模拟.同样如图3(d)所示，谐振子在相空间的量子统计分布也不能用初始动量为高斯分布的大量经典谐振子的相空间轨道来进行模拟，所以量子动力学给出的概率统计是全局动力学相干的，其空间概率分布是全空间相关联的结果.当然当谐振子能量很大的时候谐振子经典相空间轨道和量子的环面会越来越接近，因为能量涨落(环的宽度)在大能量下基本可以忽略.

5 结束语

综上所述，经过我们对宏观和微观谐振子的进一步研究发现，经典谐振子与量子谐振子的统计分布既有严重的分歧又有某些必然的联系， 量子谐振子的行为只能在一定条件下趋近于经典谐振子而不可能完全等同[4].本次工作借助Mathematica软件的数值计算和图像展示功能，使比较抽象的谐振子问题变得更加形象和容易理解，通过比较谐振子系统的经典统计分布与量子统计分布为进一步理解相关物理规律奠定了基础.