角位移矢量性的进一步探讨
2021-07-04王靖洲
王靖洲
(贵州省凯里学院 理学院,贵州 凯里 556100)
1 问题的基本分析和推导
角位移和角速度是否是矢量,以及为什么有限转动的角量不是矢量,而无限小转动的角量却是矢量,很多文献[1-8]都进行了分析解答.这些文献主要都从矢量加法应该满足交换律来论证.
对先后两次转动若用矢量A、B表示,结果则为A+B,当把转动的次序交换,结果则为B′+A′,最后如果得到A+B≠B′+A′,则因为不满足加法交换律,从而得出有限转动不是矢量.文献中主要用两个方法进行论证.一是通过直观图形中位形来表示,从而得出是否满足矢量交换律[1].二是利用张量计算公式,最后比较计算结果.典型的计算如下所述[2].
(1)
(2)
把式(1)代入式(2),得
(3)
(4)
(5)
(6)
把式(5)代入式(6)得
(7)
(8)
转动次序交换后的两结果不相等:
(9)
但当假设φ→0、θ→0,则有sinφ→φ,cosφ→1,sinθ→θ,cosθ→1,于是式(4)和式(8)分别为:
(10)
(11)
此时仍然有
只有再次略去二阶无穷小φ·θ→0时,才有
(12)
所以有限转动不是矢量,无限小转动在忽略二阶以上的无穷小时,满足交换律,因此,无限小转动是矢量.并且由式(10)和式(11)还看出,在忽略二阶以上无穷小时,当去掉转动张量主对角线上元素后,转动张量是反对称的.
2 数学分析和结论
从张量计算形式来看,对两个有限转动的转动效果相加,对应两个转动矩阵的相乘.而对于两个真矢量的相加,是简单的求和运算,是真正的相加,满足交换律.例如对于任意两个真矢量,
C=x1i+y1j+z1k,D=x2i+y2j+z2k
则
C+D=(x1+x2)i+(y2+y2)j+(z2+z2)k
(13)
也可以表示为矩阵形式:
C+D≡D+C
(14)
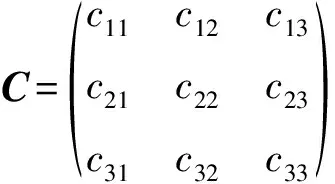
也有:
C+D≡D+C
(15)
由式(4)、式(8)可见两次转动的“相加”,对应矩阵的乘法,需要9个数来描述.由矩阵的乘法也可知,一般是不满足对易性的,A·B≠B·A,并且还可能出现A≠0,B≠0,但A·B=0的情形.所以矩阵乘法时,它们的位置很重要,并不能保证一定满足交换律.
3 物理分析及意义
根据前面的分析,整理成下面3个物理问题,帮助初学者彻底弄清转动的物理实质:
1) 为什么矢量加法必须满足交换律?加法交换律的物理实质是什么?
2) 描述转动要用张量,满足什么条件时又会变为一个矢量?
3) 这样的矢量有什么特性,它的物理本质是什么?
对于问题1),首先有必要回顾一下矢量的定义.接触得多的矢量的一种定义是:既有大小,又有方向,运算遵守平行四边形法则的物理量.在接触到张量概念后,矢量还定义为:一个由3个数唯一确定的不变量,它不会随着坐标系的变化而变化.这种定义指出了“量”的显著特征就是不随坐标系的变化而变化,便于从标量、矢量、张量角度进行概念的延伸.当两个矢量相加时,相当于将一个矢量沿着另一个矢量平移,在平移过程中,由于坐标轴不会随着平移而变化,且相对独立,(见式(11)与图1),所以“和”的3个数由原矢量对应的3个数分别求代数和.代数和是满足加法交换律的.矢量加法就是矢量平移,加法交换律就是平移的次序无关性.平移次序无关性的物理本质,就是空间对平移是均匀的、各向同性的.

图1 坐标平移
对于问题2),先回顾一下张量的一个性质:任何张量都可以被表示成对称张量与反对称张量之和.
Tij=Sij+Aij
(16)
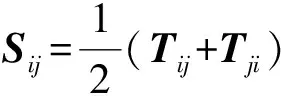
对于Sij,通过选取恰当的坐标系,可以实现对角化,对角线上3个元素对应3个坐标轴,从而等效为一个矢量,这称为化张量到主轴.
对于反对称张量Aij,取其各元素为
并且由定义有a12=-a21,a13=-a31,a23=-a32.
6个元素中两两相关,所以只有3个数是独立的,有成为矢量的可能性.把符号代入为
(17)
为得到反对称张量与矢量的可能对应关系,比较一下张量乘法与矢量乘法的结果.
(18)
(19)
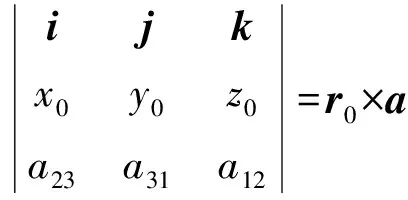
取相反数,在物理上意味着方向相反.只一个坐标轴反向时,被称为反射.当所有坐标轴都取反向时,被称为反演.从式(18)、式(19)以及行列式的结果得出,两个矢量乘法次序的交换,全部分量都反号,等价于反演.如图2所示:图2(a)为原坐标系,且x、y、z的方向遵循右手螺旋关系,当反演后变为图2(b),此时不遵循右手螺旋关系,而遵循左手螺旋关系,说明反演让坐标系的螺旋关系发生改变.再让Oyz平面绕x轴顺时针转动180°,变为图2(c).(a)与(b)所有轴都反向,是反演关系.(a)与(c)只是x轴反向,是反射关系.(b)与(c)是转动关系.(a)是右手螺旋,(b)和(c)都是左手螺旋.左右手对称性也被称为宇称,可见反射和反演改变宇称,但转动不改变宇称.在坐标系宇称是否变化上,反射与反演等价.
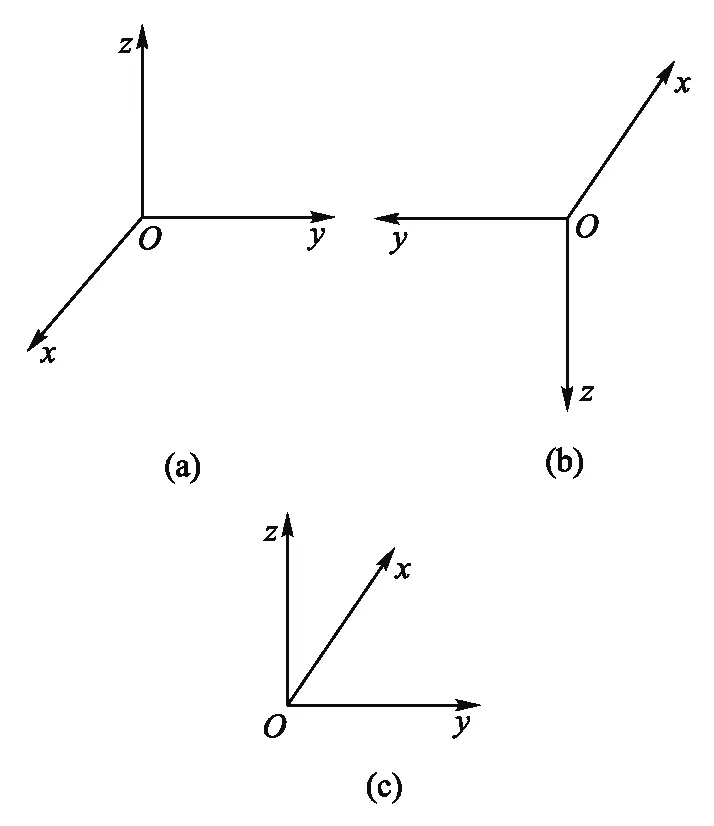
图2 坐标系类型及变化
现在可以回答问题2):转动张量只在反对称时候,就能变为一个形式上的、只需要3个数描述的量,相当于矢量.
为了弄清这样的矢量有什么性质特点,有必要把标量、矢量、张量三种量重新定义为:标量是仅需一个数就能唯一确定的不变量,矢量是用3个数确定的不变量,张量是至少要9个数确定的不变量.这三种量都有一个统一的特性:不变性.在坐标变换时,它们分量虽然会变化,但是“总量”不变.并且会保持变换规律不变,也把这一标准作为一个量是否是张量的标准.有时把标量、矢量当成是张量的特例,统称为张量.
因为转动张量等价于两矢量的叉乘,所以为了得到转动张量的性质特点,可以通过两矢量的叉乘在坐标变换下的特点为例进行分析研究.假设存在矢量A、B,且定义它们的叉乘,即A与B叉乘有C=A×B,用分量表示为Ci=AjBk-AkBj,且设坐标变换为
(20)
通过比较先进行坐标变换再叉乘、先叉乘再进行坐标变换的结果,来研究C的特点.
先坐标变换再叉乘的运算过程如下:
根据张量的运算法则:
(21)
(22)
(23)

(24)
(25)
(26)
先叉乘再坐标变换的运算过程如下 :
C1=A2B3-A3B2
(27)
C2=A3B1-A1B3
(28)
C3=A1B2-A2B1
(29)
(30)
由式(27)至式(30),得到
(31)
(32)
(33)
可见在同一坐标变换方式下,只是由于运算的次序不同,而得到两组互为相反数的结果,说明由C=A×B定义的“矢量”C,不满足真矢量在坐标变换下的不变性,因此不是一个真矢量,被称为赝矢量、轴矢量,而真矢量也被称为极矢量.
为什么此例中坐标变换后会是这样的结果,下面从分析坐标变换本身入手.由式(20)知a21=-1,其坐标变换为x→-y′,a13=1对应坐标变换为z→x′,a32=1对应y→z′,如图3所示最终由图3(a)变到图3(d),可认为经历了绕y轴转90°到图3(b)图所示,再绕x轴转90°到图3(c)图,再沿Oxy平面反射.再如图4所示,初态(a)和末态(d)分别与图3的(a)与(d)相同,经历的过程不同.先反演图4(b)图,再绕y轴转90°至图4(c)图,再绕x轴转90°.除了转动,还有反演或反射,正是反演(反射)的存在,导致变换规律的变化,从而C不是矢量.同时还可发现,转动的次序是不变的,都是先绕y轴转,再绕x轴转,否则图3和图4不能得到一致的结果.
把反对称张量退化成一个矢量来表示,当存在反演(或反射)时,坐标系的螺旋性必定发生变化,变换规律也一定发生变化,所以它不是一个真矢量,是一个赝矢量.这就是转动矢量不是真矢量、矩阵乘法运算不对易的本质原因:空间对于转动,有左旋和右旋的区别.

图3 aij对应的坐标变换1
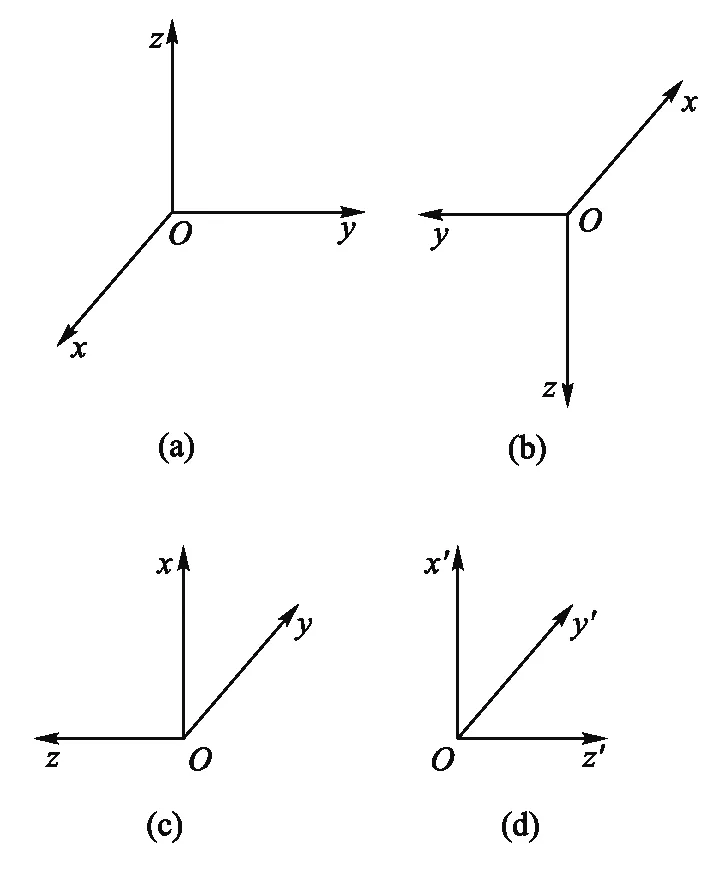
图4 aii对应的坐标变换2
4 结论与展望
文献1中两个例子:有限转动和无限小转动,恰好是前者改变了螺旋性,后者没有,所以得到前者不是矢量、后者是矢量的结论.在有限转动例子中,若按顺序轮换x→y、y→z、z→x式的转动,即先绕x轴,再绕y轴,或先绕y轴,再绕z轴,或先绕z轴,再绕x轴,所得结果就会完全一致了.
对此,严格地讲矢量加法的交换性对转动不能成立.应该让学生明白,转动张量或矩阵乘法不对易的根本原因是:空间对转动具有右手螺旋和左手螺旋差异.
弄清物理本质是物理教学的核心要义,只有在弄清物理本质的基础上,学生才可能对物理问题进行深层次地思考与创新,而不是简单地只对计算结果的认同.
