超导量子比特

宿非凡，杨钊华,2，范 桁,2，赵士平,2

(1. 中国科学院物理研究所 北京凝聚态物理国家研究中心，北京 100190；2. 中国科学院大学 物理科学学院，北京 100049)

早在上世纪70—80年代，约瑟夫森结以及超导量子干涉器件(SQUID)中的宏观量子隧穿、能级量子化、共振隧穿、光子诱导跃迁、布居数反转等量子特性就引起了研究人员的广泛兴趣.世纪之交的1999年，日本NEC的研究组利用约瑟夫森结的特性成功制备了第一个超导量子比特(电荷量子比特)，测试结果首次展示了持续约2 ns的量子相干振荡[1].此后不久Jonathan Friedman与John Martinis研究组等也分别成功制备了具有不同设计结构的超导量子比特，按照其设计原理可以分为位相量子比特[2]与磁通量子比特[3]两类，后面发展出来的新型量子比特基本都可以看作上述三种量子比特的变形.量子系统的相干时间是该系统的“寿命”，较长的相干时间是超导量子比特参与量子物理研究和量子计算的必备基础.在2018年提出的超导量子比特“摩尔定律”，该定律指出超导量子比特的退相干时间几乎在5年提升一个数量级，经过近20余年在器件设计、制备材料、制备工艺与测量方法等方面的不断努力，超导量子比特的退相干时间已经有了近4个数量级的长足进步[4].另一方面，各个研究组以耦合超导量子比特形式对存在量子纠缠的量子比特数目进行了明显的扩展，2019年谷歌的“悬铃木(Sycamore)”量子比特芯片上量子比特的数目已经达到53个[5].这些进步为后续的研究打下了有效的基础，利用超导电路和量子比特搭建的量子计算平台可以对量子物理学，原子物理学，量子光学，量子化学等领域的诸多问题进行研究和模拟.正因为超导量子计算具有比特数目易扩展，与成熟微波系统兼容性好，量子态制备方便，样品退相干时间提升空间广阔等特点，因此超导量子比特也成为最有希望实现普适量子计算(通用量子计算)的方案之一.

本文主要介绍不同类型的超导量子比特的基本原理和结构组成，同时介绍超导量子比特的制备工艺和量子态的测量技术，以及利用超导量子比特对特定问题开展的研究内容，以期阐明超导量子比特以及超导量子计算的一般原理与方法.

1 超导量子电路与量子比特

超导量子比特芯片上的电路在正常工作的情况下是超导电路，构成超导电路的要素可以视为两类.普通要素与一般电路一致，包括电容器、电感和电阻(等效)，而核心要素是约瑟夫森结和谐振腔.要理解超导量子比特的工作原理，首先需要理解约瑟夫森结的宏观量子现象原理.根据超导体的BCS理论，超导体中电子将组成电荷量为2e，质量为2me，自旋为零的库伯对，其状态可以用波函数ψ(r,t)来描述.对于超导量子比特而言，有两点超导体性质需要着重理解.第一点是磁通量子化，当一有磁场穿过的闭合回路环达到超导转变温度以下温度后，如果此时去掉磁场，那么该闭合回路环中的超流产生的磁通量是量子化的，该磁通量子为φ0=h/2e≈2.07×10-15Tm2，磁通量子化的性质要求波函数ψ(r,t)是单值波函数.第二点是约瑟夫森隧道效应，约瑟夫森结由上下两层超导体中间夹一个厚度一般为2～3 nm的绝缘层组成，库珀对可以保持相干性的隧穿过绝缘层.通过绝缘层势垒的超电流I与两个超导体之间的规范不变相位差δ(t)满足约瑟夫森方程：

(1)

其中Ic为约瑟夫森结的临界电流，V为约瑟夫森结两端电势差，h为普朗克常量.由式(1)可见约瑟夫森结是一种具有非线性电感|LJ|=φ0/(2πIccosδ)的无耗散器件，这一点是超导量子比特的关键性质.因此，可以将约瑟夫森结等效为如图1(a)的RCSJ模型电路结构，在这个模型中约瑟夫森结等效为电容、电感和超流3个部分.由基尔霍夫定律可以对该模型写出Itot=I+CdV/dt+V/R，进一步可以得到该系统的动力学方程：

(2)

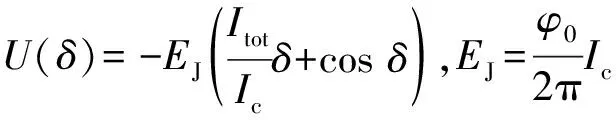
图1 RCSJ模型及其势能曲线

有了上述的基础，可以看到如果在实验中控制电流Itot即可控制搓衣板势垒的高度与能级间距.当Itot/Ic≥1时势阱消失，此时可以形象的理解为准粒子会顺着势能曲线向下一直运动，根据约瑟夫森方程，这时约瑟夫森结超导体两端将存在电势差，而Itot/Ic<1 时势阱存在，准粒子处于势阱中，约瑟夫森结超导体两端不存在电势差.且在势阱较浅时，准粒子将有一定的概率隧穿出势阱，约瑟夫森结超导体两端也会从无电势差转变为有电势差.这样一来，约瑟夫森结就可以在宏观上表现出可以探测的“量子性”.

1.1 位相量子比特

位相量子位原理上可以看作由电流偏置约瑟夫森结构成，如果将搓衣板势阱中的最低两个能级作为量子比特的|0〉态和|1〉态(类似经典计算机的0、1两个电位状态)从而进行量子计算.当势垒足够高时利用微波脉冲调控即可将位相量子比特进行初始化.接下来调整适当的势垒高度使得准粒子可从势阱中隧穿出来，根据上面的讨论可以知道此时测量约瑟夫森结超导体两端的电势差即可读出系统的量子态.

除了上面提到的控制电流Itot来控制搓衣板势垒的高度与能级间距，为了减少偏置电流引入的噪声对位相量子比特的影响还可以配合Rf-SQUID将磁通φ作为实验可控参数.如图2所示，该种设计结构对应的方程可写为

(3)

其中φe为外加磁通，Φ=φtot/φ0，U(φ)=

βL=2πLIc/φ0(L为环电感).

图2 磁通偏置的Rf-SQUID位相量子比特结构示意图

在实验中，一般要求1<βL<3.5以使得势阱为图3所示的双阱形式.此时通过改变线圈中外加磁通φe来使势阱势垒提高或降低，此后便可选择适合测量系统的能级作为量子比特的两个态.

图3 Rf-SQUID型位相量子比特的势阱与能级

利用多层膜工艺制备的Rf-SQUID型相位量子比特实物照片[6]如图4所示，该器件的设计与UCSB设计相似，在该设计中的SQUID包含3个约瑟夫森结一个小结与两个较大的串联连接，大结的临界电流是小结的1.7倍，这种设计的优点是不需要单独测量外加磁通φe.

图4 射频Rf-SQUID型相位量子位元的光学照片(方框和圆圈位置分别量子比特与SQUID探测器约瑟夫森结区[6])

1.2 电荷量子比特与传输子量子比特

电荷量子比特是历史上最早一种量子比特设计[3]，其设计示意图如图5所示.将一个门电容Cg与一个约瑟夫森结串联，二者可由门电压Vg进行偏置.该体系的哈密顿量为H=(Q-CgVg)2/2(C+Cg)-EJcosδ其中Q=2en表示门电容与约瑟夫森结电容中的总电荷量.如果用电荷数表示哈密顿量，则可以写为

H=4EC(n-ng)2-EJcosδ

(4)

其中n为库珀对电荷数，ng=CgVg/2e，EC=e2/2(C+Cg)为电荷能.电荷量子位工作在EJ/EC远小于1的电荷能EC占主导地位的区域，图6为EJ/EC=0.2时电荷量子比特的能谱，可见电荷量子比特的能级会随着n的变化而发生周期性变化，Nakamura等首次在这种电荷量子比特中观察到持续ns量级的相干量子振荡[1].

图5 电压偏置超导电荷量子比特结构示意图

图6 EJ/EC=0.2时的电荷量子比特能谱

在EJ/EC远大于1的约瑟夫森能EJ占主导地位的区域，如图7所示(EJ/EC=50)，此时能谱平整且各个能级间距并不随电荷数n发生周期性的变化，也就是说此时量子比特对电荷噪声不敏感，这无疑会提高量子比特的相干时间.在实验中可以选取如图8所示传输子量子比特的势阱中最低的两个能级被用作量子比特|0〉态和|1〉态.

图7 EJ/EC=50时的电荷量子比特能谱

传输子量子比特正是Koch等人利用上述考虑由电荷量子比特改进设计而来[7]，较之电荷量子比特，传输子量子比特在相干时间上有着质的提高，目前所报道传输子量子比特相干时间平均在30～50 μs.

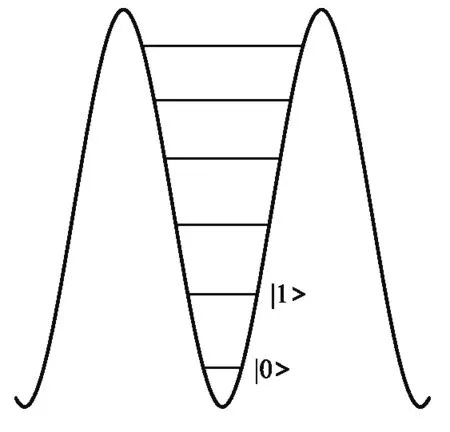
图8 传输子量子比特的势阱与能级

在实验上，可以通过将电容器与约瑟夫森结平行连接在一起来并由门电压Vg进行偏置来设计传输子量子比特.如图9(a)所示为3D腔中的传输子量子比特[8]，放大部分是中心有约瑟夫森结的量子比特，两个大垫片一边是电容器电极，另一边时用来读取量子比特状的耦合谐振器，此外该谐振腔也可以使量子比特不受外界环境电磁噪声的影响.这种3D腔中的传输子量子比特拥有能量弛豫时间T1=60 μs、相干时间T2=20 μs的良好性能.如图9(b)所示2D传输子量子比特的图片[9]，其中两个大的平板是电容器的两个电极，约瑟夫森结位于中心电容器极板间的中央位置，底部两个面积较小平板用于该量子比特与其他量子比特的电容耦合，而量子比特状态的测量则依靠图中顶部的小平板实现，这种2D的传输子量子比特虽然稍逊于3D传输子量子比特，其能量弛豫时间也可以达到T1=30 μs、相干时间可以达到T2=20 μs.

(a) 3D传输子量子比特 (b) 2D传输子量子比特 光学照片[8] 光学照片[9]图9 3D与2D传输子量子比特

Xmon量子比特是UCSB的John Martinis研究组对传输子量子比特的一种优化设计[10]，Xmon量子比特的中心是一个十字电容结构，并将传输子量子比特中的单约瑟夫森结用双结设计替换.这种设计使得Xmon量子比特的状态可以更加方便地调节并由耦合读出谐振腔读出(后面将详细讨论)，也更容易与其他量子比特或其他后续需要的谐振腔耦合在一起，从而可以简单的在量子比特数目上加以扩充.

如图10所示，Xmon量子比特十字结构的4个臂分别连接到XY控制、Z控制、由于与其他量子比特电容耦合以及与用于量子比特状态读出的谐振腔耦合起来.目前报道的Xmon量子比特的能量弛豫时间平均达到40 μs，这种设计的易扩展性与优秀的相干时间使得Xmon量子比特成为目前各种研究中最常见的一种超导量子比特.

图10 Xmon量子比特光学照片、Xmon量子比特等效电路结构图以及约瑟夫森结区光学照片[10]

1.3 磁通量子比特

Mooij等人于1999年提出了磁通量子比特的设计.如图11所示，其由3个约瑟夫森结组成的超导环构成，3个约瑟夫森结其中一个结的面积比另两个结要小α倍.该设计中约瑟夫森提供了较大的电感，与面积较小的约瑟夫森结并联电容的小回路的电感可以忽略不计，这使得它对外部噪声不太敏感.由于每个约瑟夫森结都存在一个搓衣板势，因此磁通量子比特的势能为如图12所示的二维形式，其表达式为

U(δ1,δ2)=EJ(2-cosδ1-cosδ2)+

αEJ[1-cos(2πf+δ1-δ2)]

(5)

其中δ1于δ2分别为两个大结的相位差，2πf=-(δ1-δ2+δ3)，δ3为小结的相位差.图13所示的双势阱势能曲线为沿图12中红色线段所截取的部分.可以通过改变α来实现调节两分立势阱的高度，一般情况下α的数值在0.5～0.7或低于0.5的范围内，在这个范围内处于两个能级的准粒子比较容易在外加磁通φe=φ0/2的条件下发生隧穿.由于|0〉态和|1〉态对应于磁通量子比特环中具有相反方向的电流，因此作为量子比特的两个态可以在实验上较为方便的被探测到.

图11 磁通量子比特原理示意图

图12 式(5)所描述的二维势的等高线图

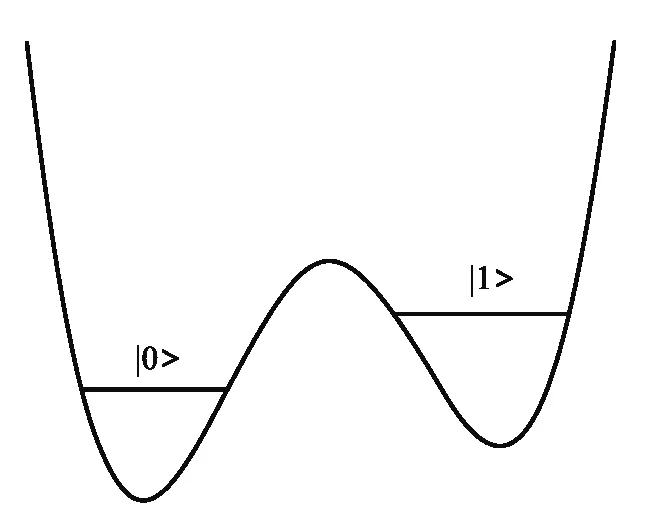
图13 φe=φ0/2时沿图12中实线所指示方向的势阱与能级(两个势阱中状态对应于量子比特环中具有相反方向的电流)

进一步的研究显示，磁通量子比特的相干时间较强的依赖于α的取值，当其数值降低到0.5以下时，磁通量子比特拥有双势阱的特征会随着势垒高度的降低而减弱，通量量子位将拥有与传输子量子比特相似的势阱形状，通过该途径磁通量子比特的能量弛豫时间可以达到80 μs，此外近年来更多的研究报道显示磁通量子比特的性能仍有着较大的提升空间.

回顾超导量子比特的发展，最早的电荷量子比特只有ns量级的相干时间，而从电荷量子比特改进而来的传输子量子比特，因为其设计使消除了电荷噪音对其的影响，从而消除了退相干的主要来源，使得量子比特的相干时间提高到100 μs量级.而且传输子量子比特的设计结构简单，在制备工艺上较之早期的位相量子比特等有了极大程度上的简化，加之在过去的10年中，人们对二维谐振腔的介电损耗以及提升量子比特性能的方法进行了详细的研究.这些因素使得目前人们对于近期内实现相干时间可达ms量级、纠缠量子比特数目达到100个以上、拥有极高保真度的量子比特芯片充满信心.

2 超导量子比特的制备

量子比特的制备工艺流程与半导体芯片制备工艺相似，其大致可以分为版图设计、流片、封装与测试三大部分.但是要实现高性能的量子比特器件，在制备工艺、基底材料预处理、器件材料选择等方面都需要进行细致的研究与探索.目前主流的制备工艺路线是在蓝宝石基片上生长金属铝薄膜，此后利用光刻与金属刻蚀工艺转移设计图形制备超导电路并在超导电路的指定位置上利用金属铝双角度蒸发的方法制备符合器件设计要求的约瑟夫森结，最后将制备好的量子比特进行复查检测、切割和超声点焊封装.

John Martinis研究组于2014年发布的总结性报告[11]中详细的阐述了其对基底材料的介电损耗、附加电感等关键性质，实验中制备约瑟夫森结的能量损耗机制，芯片上超导电路线路能量损耗等的系统性研究结果.近年来，人们对于基底材料预处理方法的研究表明，基底材料的洁净度与量子比特的退相干时间有着直接的关系，在运用“食人鱼”溶液预处理并高温退火的蓝宝石基片与高祖硅基片上制备的量子比特的相干时间都得到了不同程度的提高.此外，一些新的金属材料，例如金属铌与钽替换金属铝制备超导电路的量子比特也显示出自己独特的优点，这些新工艺、新材料制备的Xmon量子比特的能量弛豫时间最长可以达到0.3 ms，而利用这些新材料工艺制备的超导量子计算辅助参数放大器则可以在10 mK的极低温环境下达到放大频率有效范围600 MHz，增益20 dB，噪声水平接近量子极限的水平.

超导量子比特制备工艺中最关键的部分是高质量约瑟夫森结的制备.约瑟夫森结有很多制备路线，但对于超导量子比特器件的约瑟夫森结只有两种主流工艺，一种是夹心饼工艺，另一种是多兰桥(Dolan-Bridge)工艺[12].兰多桥设计与电子束曝光(EBL)是制备超导量子比特核心部分约瑟夫森结中的主流工艺[6].由于电子束的物质波长比紫外光刻工艺中的光波长小得多，因此该工艺可以精确的定义出更小的精细结构.电子束曝光约瑟夫森结的图形设计如图14(a)所示，该设计利用T字形和横线的图形组合通过双层光刻胶(MAA+PMMA)电子束曝光工艺得到悬空的PMMA桥.此后再通过沿着特定角度蒸发一层厚50 nm的金属铝，送入氧化室氧化后再垂直于平面蒸发一层厚100 nm的金属铝，最后对样品进行铝薄膜剥离就完成了约瑟夫森结的制备，制备的约瑟夫森结扫描电镜照片如图14(b)所示.一般来说，在制备工艺中约瑟夫森结结区的面积大小与蒸发的角度与线条宽度两个因素有关.而当蒸发角度超过临界值后，约瑟夫森结面积便与蒸发角度无关，正因如此采用T字形和横线的组合设计可将影响约瑟夫森结结面积大小的因素固定在线宽上，也就是说在一次实验中相同曝光条件下制备约瑟夫森结结面积的均匀性更好，这为超导量子比特数量的扩展打下了工艺基础.

(a) 约瑟夫森结设计图 (b) 约瑟夫森结区电照片图14 约瑟夫森结图

对于多超导量子比特的芯片来说，各个量子比特之间的串扰会影响后续对量子比特的操控与读出，为了减少这种有害的串扰需要在量子比特的超导电路上制备数千条金属“桥”以在不影响超导电路功能的前提下使各个部分的电势相等.金属“桥”有两种制备思路，一种是通过绝缘层将超导电路的谐振腔保护起来后在绝缘层上生长金属薄膜连接绝缘层两端的金属薄膜，另一种是直接制备拱起跨过谐振腔的空气桥(Air bridge).由于绝缘层材料会改变谐振腔的微波特性，因此目前的多量子比特制备工艺中一般选择空气桥工艺，上述两种垮桥工艺制备的跨桥分别如图15(a)、图15(b)所示.

(a) 在绝缘层上制备的跨 (b) 空气桥光学照片 桥光学照片图15 空气桥

3 量子非破坏性测量

对量子比特状态快速、准确的读取是超导量子计算的基础，目前各个研究单位广泛采用的测量方案是基于电路腔量子电动力学(cQED)结构的量子非破坏性测量(QND)技术.与使用直流SQUID探测量子态的方案相比，基于cQED的量子非破坏性测量拥有许多优点，其中最显著的有优点是QND不破坏量子比特的量子态并显著提高了测量的速率.该技术经过不断的发展，从一开始的专用在传输子量子比特与Xmon量子比特到目前亦可以用于位相量子比特与磁通量子比特的测量，可以说QND已经成为被广泛应用的一项通用技术.

4 基于超导量子比特的实验研究

超导电路和超导量子比特因具有宏观量子效应，系统参数易于控制，制备方便，可扩展等优点为研究量子物理、原子物理和量子光学的问题提供了一个很好思路和硬件工具.在利用超导量子比特的量子模拟实验中，被模拟的量子系统哈密顿量可以直接被映射到被实验直接控制的超导量子比特体系哈密顿量上.因此，基于超导量子比特的超导量子模拟在量子物理、量子化学、凝聚态物理、宇宙学和高能物理等学科的研究中较之经典计算机有着天然的优势.近年来，人们利用超导量子比特对量子光学中的强驱动下非线性系统的共振逃逸和分岔现象、凝聚态物理中铜酸盐材料中的宏观量子隧穿和量子态中的相扩散现象、耗散量子系统中的量子随机同步现象、相互作用量子系统的拓扑相图和相变、薛定谔猫态、量子光学中Autler Townes劈裂现象、受激拉曼绝热通道的相干群转移问题、电磁诱导透明、共振荧光和相关发射激光等诸多方面的研究都有获得了很好的成果,此外中科大和物理所合作还在12比特链状和 24比特阶梯状系统中完成了量子行走问题的研究，首次发现激发态的传播在这两个系统中有着很大的区别.由于篇幅所限，对于更多的进展这里就不做展开介绍了.

当然，人们对于量子计算的终极目标就是实现一般性的量子计算机.早在20世纪80年代，美国物理学家Richard Feynman就提出了量子计算机概念[13]，20世纪90年代中期，Shor和Grover分别提出了两种展示量子计算机在计算能力上对经典计算机拥有绝对优势的量子因子分解算法和量子搜索算法.2019年，谷歌宣布实现量子霸权[5]预示着一般性的量子计算机距离我们越来越近，目前基于超导量子比特的超导量子计算与其他量子计算方案一起成为众多不断探索物理世界的科学家追逐共同理想的有力工具，也逐渐成为了一个站在物理学前沿富有生命力的边界日益拓展的理论与现实的集合体.

5 结语

通用量子计算机可以给人类带来前所未有的强大计算能力，借助这种强大的计算能力人类将在天气预报、药物研制、交通调度、保密通信、基础科学理论等方面都将实现质的飞跃.实现通用量子计算的理想是量子计算技术创新的巨大动力，自约瑟夫森器件的量子相干特性得到展示以来，在不到25年的时间内，不论在超导量子比特的设计上还是在器件性能上人们已经取得了显著进展.超导量子比特的相干时间从2 ns最高提升10万倍增加到0.3 ms，纠缠量子比特数目从2个增加到53个，信息读出的保真度与信息纠错能力不断增强，超导量子计算在诸多科学问题的研究中崭露头角.目前来看，建造通用量子计算机所需的大多数基本条件和功能正在逐渐实现.可以预见并值得欣喜的是，在朝着实现这一最终目标前进的路途中，人们将继续在量子物理、原子物理、量子光学、非平衡态量子物理和量子模拟等研究中取得更加丰硕的成果.可以肯定的是，今天是人类从结绳记事开始在实现通用量子计算机的正确道路上距离它最近的一天.