窄间隙摆动电弧数值模拟

徐 刚， 张天雷， 何林基， 沈艳涛， 马春伟

(1.上海工程技术大学 材料工程学院， 上海 201620； 2.北京遥感设备研究所， 北京 100854；3.北京海基科技发展有限责任公司， 北京 100192)

窄间隙焊接是一种采用较小坡口角度的高效焊接方法，具有填充焊材量少，热输入低，焊缝力学性能好，生产效率高及制造成本低等优点[1-2]。但是，窄间隙焊接容易产生根部和侧壁未熔合的现象[3]。所以研究窄间隙焊接电弧的物理特性就变得十分重要。但电弧的物理过程十分复杂，通过试验手段很难对其进行分析，而流体仿真计算提供了较好的分析途径。

目前，国内外学者已经对等离子弧焊及非熔化极惰性气体保护电弧焊(tungsten inert gas welding, TIG)电弧做了大量数值计算相关工作。殷凤良等[4-5]建立了完善的等离子焊的电弧模型，并建立了等离子弧焊电弧反翘模型。贾剑平等[6]建立了旋转TIG电弧模型，但目前没有开展与窄间隙焊接电弧相关的数值计算工作。

课题组借鉴了众多学者对等离子弧焊及TIG焊电弧的模拟计算分析思路，使用流体计算软件FLUENT，并对其用户自定义函数(UDF)进行二次开发，求解磁流体动力学相关方程。不考虑金属蒸气，不考虑熔滴过度，简化保护气化学成分，研究窄间隙焊接的电弧特性。

1 数学模型

1.1 基本假设

基本假设：电弧区域为导电的纯氩气环境，等离子体参数仅为温度的函数；电弧处于稳态，且不可压缩；电弧处于层流状态，为稳定的连续介质；电弧关于中心平面对称；电弧等离子体处于局部热平衡(local thermal equilibrium，LTE)状态；电弧是光学薄，即电弧对热辐射的重新吸收相对于电弧的热量损失可以忽略不计；忽略熔滴过渡及金属蒸气对电弧形态的影响；由于黏性效应导致的热损失忽略不计。

1.2 物理模型

对于窄间隙电弧数值计算，由于其焊接空间的局限性，保护气的流动状态受侧壁约束，将沿焊道流出焊接空间。若采用二维数值计算模型，会导致速度场与实际相差较远，所以课题组使用电弧三维模型进行数值计算。图1所示为窄间隙电弧计算域示意图。其中ABCDEFHI为对称平面，EFGHI为焊丝，AIEDMJ为保护气入口，JMLK为保护气出口，ABCDMLKJ为窄间隙焊缝表面。

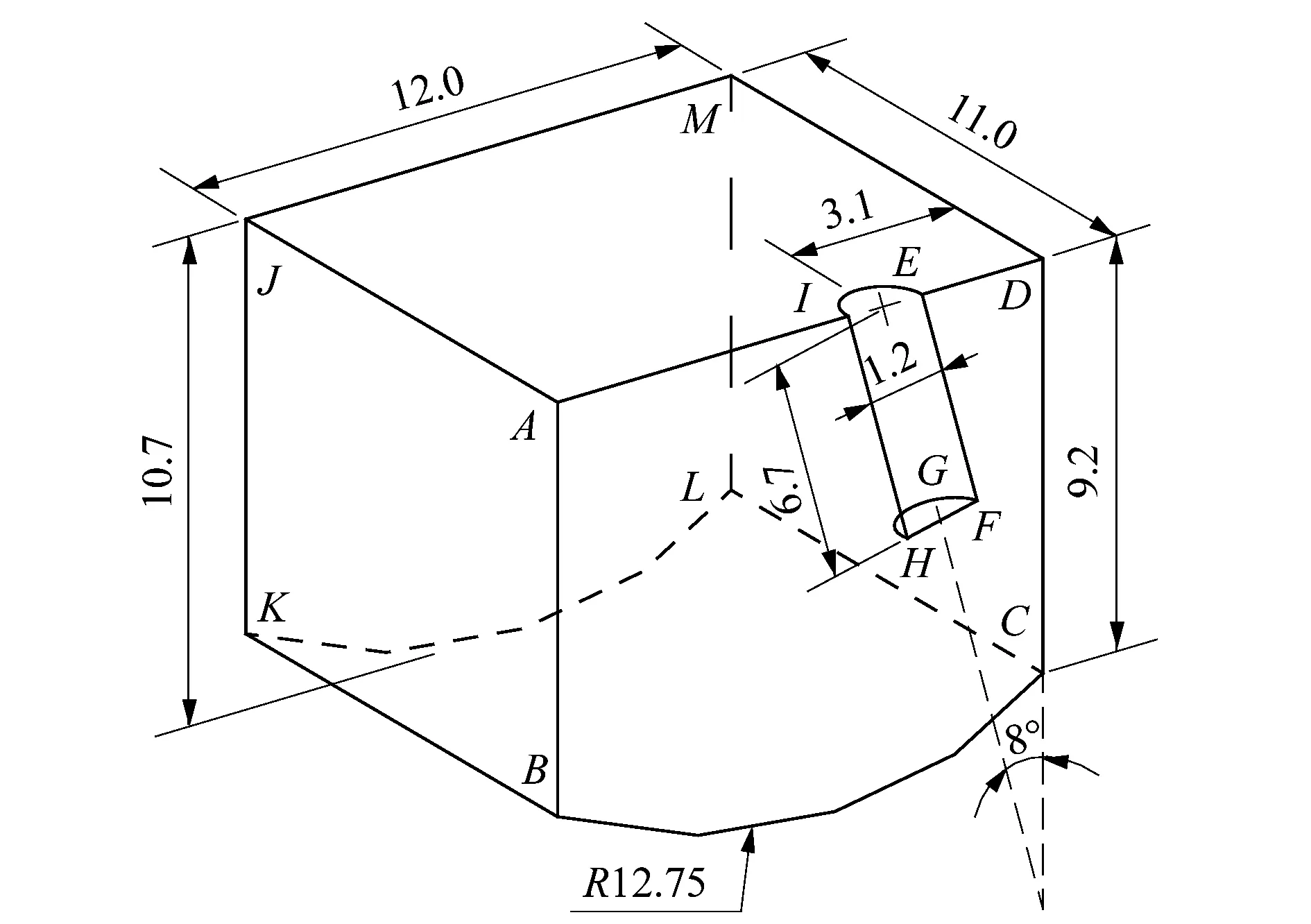
图1 电弧的计算区域Figure 1 Computational domain of welding arc

课题组使用SolidWorks建立电弧计算域几何模型，用HyperMesh划分计算域流体网格，电弧区最小网格尺寸为0.1 mm，网格形式如图2所示。

图2 网格模型Figure 2 Mesh model

1.3 控制方程

电弧实际是一种导电的流体，可通过磁流体动力学中的Navier-Stokes的控制方程和麦克斯韦电磁方程组进行描述。

1.3.1 Navier-Stokes的控制方程

1) 质量连续方程

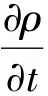
(1)

2) 动量守恒方程

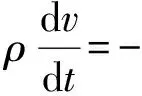
(2)

3) 能量守恒方程

(3)

式中：ρ为等离子体密度；t为时间；v为速度；P为压力；μ为黏性系数；H为焓值；cp为定压比热容；k为导热系数；Sr为辐射流密度；Φ为耗散功率；B为磁感应强度；σ为电导率；J为电流密度。

1.3.2 麦克斯韦电磁方程组

1) 电流连续方程

(4)

2) 欧姆定律

(5)

3) 安培环流定律

(6)

式中：φ为电势；μ0为真空磁导率。

1.4 边界条件

表1所示为计算域边界条件。其中vgiv为保护气流速，焊丝及母材熔点设为2 000 K。

2 计算结果与分析

计算所用参数为实际窄间隙焊接工艺参数，其中电流为310 A，电压为28 V，保护气流量为30 L/min，焊丝直径为1.2 mm，其他工艺参数见表1。计算使用的氩气热物理性能数据选自参考文献[7]。使用FLUENT求解出窄间隙焊接电弧的磁场、电场、速度场、压力场及温度场，并用tecplot进行后处理，得到如下结果。

表1 焊接工艺参数

2.1 窄间隙对电弧磁场的影响

图3所示为在电弧对称平面上距离焊丝端部不同位置的磁感应强度对比图。从图中可以看出，电弧轴线附近，电弧边缘及侧壁处的磁感应强度较小。电弧轴线附近磁感应强度规律与文献[8]第36页描述相符，而电弧边缘磁感应强度较小是因为边缘电流密度较小。对于侧壁处，由于部分磁场导入金属基板，使靠近侧壁处电弧周围的磁感应强度降低，导致远离侧壁处电弧的磁感应强度大于靠近侧壁处电弧的磁感应强度。电弧为达到力学平衡状态，电弧中心两侧的等离子体流动状态将有别于正常状态电弧。从图中还可以发现，从焊丝端部到熔池，磁感应强度逐渐减小，这是由于熔池表面积远大于焊丝端部表面积，使等离子体从焊丝端部流向熔池的过程中逐渐发散，即电流密度持续减小，导致磁感应强度持续下降。

图3 磁感应强度分布Figure 3 Magnetic induction density distributions

2.2 窄间隙对电弧速度场和压力分布的影响

图4所示为计算得到的电弧速度场分布。从图中可以看出，等离子体流动方向偏离焊丝轴线，指向侧壁方向。这是由于远离侧壁处电弧的磁感应强度大于靠近侧壁处电弧的磁感应强度。等离子体在远离侧壁处所受的电磁力大于靠近侧壁处所受的电磁力，等离子体的流动方向在电磁力的做用下发生偏转，直至电弧在电磁力及重力的作用下恢复平衡。图中部分流场曲线经历了保护气到电弧再到保护气的过程。这是由于电弧燃烧过程中，部分保护气在电弧区被电离参与电弧等离子体运动，复合后离开电弧区，保护熔池不被氧化，最后流出电弧计算域。图中熔池上方且远离侧壁处的等离子体并没有直接到达熔池，而是先沿熔池表面做切线运动。这是由于窄间隙焊缝底部表面为凹面，熔池附近的等离子会沿着熔池表面向焊缝凹面最低点运动。

图4 电弧速度场分布Figure 4 Arc velocity field distribution

图5所示为电弧压力场分布图。

图5 电弧压力场Figure 5 Arc pressure field

从图中可以看出，焊丝端部附近压强较大，尤其在焊丝端部压强达到最大。这是由于焊丝端部附近电弧周围的磁感应强度和电流密度都比较大，即焊丝端部附近电弧等离子体被较大的电磁力压缩，产生较大的压强。从焊丝端部到熔池，由于磁感应强度及电流密度都减小，即电磁收缩力减小，导致压强逐渐减小。但在熔池附近压强有所回升，并且压强的分布范围也在增大，这是由于等离子流冲击熔池形成的。由于等离子流受磁场影响向侧壁偏移，电弧压力分布也出现了向侧壁偏移现象。电弧对熔池的压力主要分布在侧壁根部。

2.3 窄间隙对电弧电场的影响

图6所示为计算得到的电弧电压分布图。将熔池电位定为零点参考电位，从图中可以看出，焊丝端部电位最大，随着电流流向熔池，电位逐渐减小。计算得到的两级电压为26 V，比实际电压小2 V，这可能是没有考虑熔池及焊丝端部压降的原因[8]35。除电弧底部外，侧壁同样存在较大的电势梯度，为电流流入侧壁提供势能条件。

图7所示为计算得到的电流密度矢量分布。从图中可以发现，在靠近底部和侧壁处的电流流向出现折弯现象。这是由于等离子体到达熔池前，沿熔池表面向焊缝凹面底部做切线运动，使电流密度矢量方向受到影响。由图6可知，侧壁处存在较强电势梯度，同时该处的磁感应强度较弱，当部分等离子体所受的电场力大于电磁力时，便挣脱电磁收缩力束缚流向侧壁，在侧壁与焊丝端部之间形成电流回路。

2.4 窄间隙对电弧温度场的影响

图8所示为计算所得电弧温度场分布。从图中可以看出，由于侧壁的影响，电弧温度场形态并不是钟罩形，但远离侧壁的电弧部分还保留着钟罩形态的特征。电弧温度从焊丝端部到熔池逐渐降低。这是由于熔池表面比焊丝端部表面大得多，导致焊丝端部表面等离子向外做发散运动，造成电弧温度场在熔池处也较为发散[8]40。由于等离子体向侧壁偏转，使电弧的高温区域明显向侧壁偏转，促使了电弧对侧壁及根部的加热。等离子体沿熔池向焊缝底部做切线运动的同时也增加了电弧热量的作用范围，使熔池上方的电弧低温区进一步扩大。

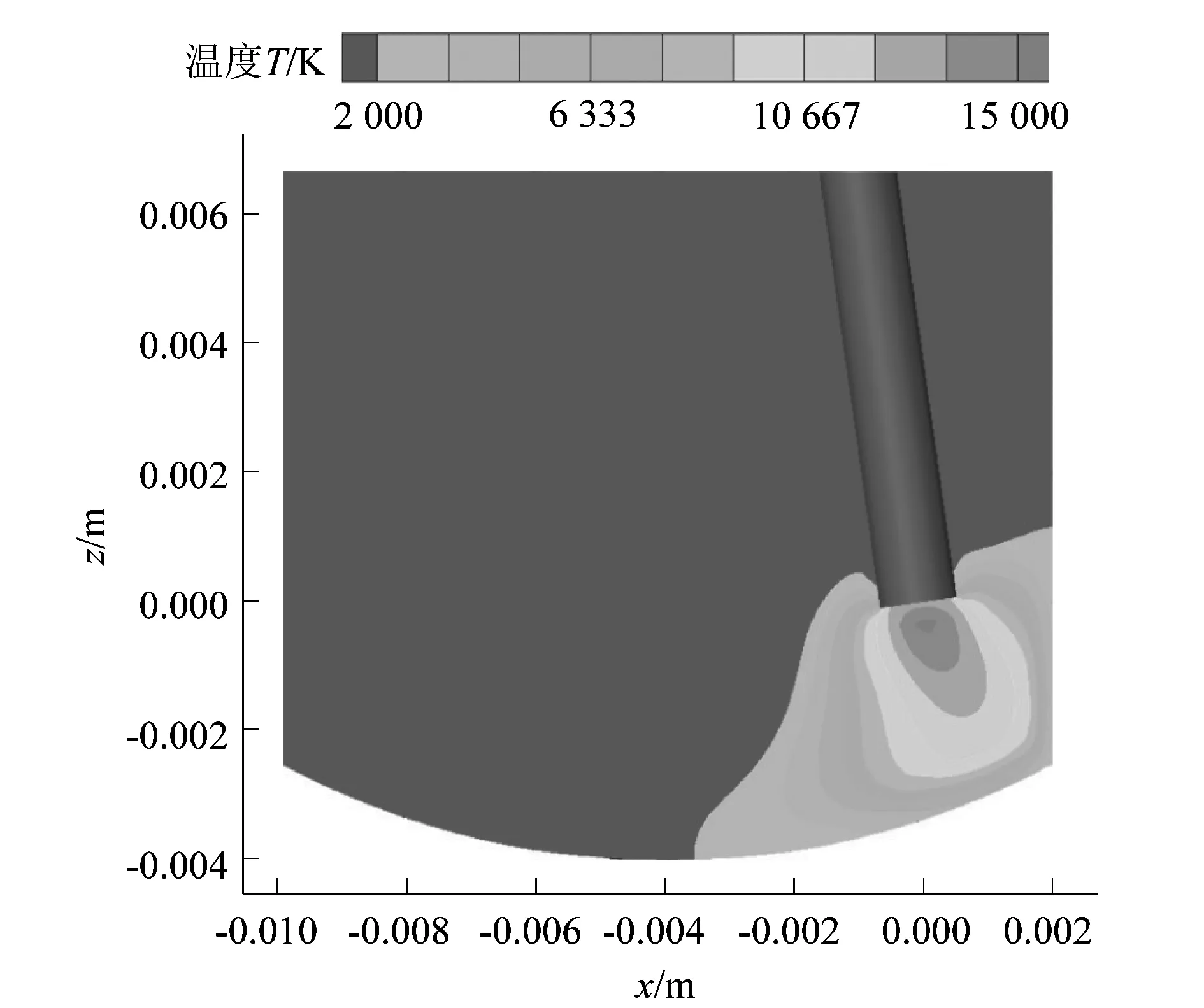
图8 电弧温度场Figure 8 Arc temperature field

2.5 电弧形态试验验证

实际电弧燃烧过程十分复杂，由电磁场、流场及温度场间相互作用形成。电弧的等离子体流速和内部温度等参数很难通过实验测定[9]。课题组通过对照实际电弧形态来验证计算结果的准确性。图9所示为相同参数下的窄间隙摆动电弧的高速摄影试验照片[10]。与计算结果对比发现，电弧温度计算轮廓与实际电弧轮廓吻合良好，这间接证明了计算结果的准确性。但实际焊接过程电弧为运动状态，为减小模型的复杂程度和计算量，使用静态模型代替电弧的瞬态过程，而且没有考虑金属蒸气及熔滴过渡，并简化保护气化学成分。计算的物理量数值与真实值可能存在偏差，但可以定性分析电弧物理特性的变化趋势。

图9 试验电弧形态Figure 9 Experimental arc shape

3 结语

1) 课题组利用磁流体动力学原理，实现对窄间隙焊接电弧的数值计算，且计算结果与试验吻合良好。

2) 窄间隙焊接过程中，当电弧运动至侧壁时，电弧的等离子流场、压力场及温度场均向侧壁偏转，从而使电弧热量集中在侧壁根部。

3) 窄间隙焊接过程中，当电弧运动至侧壁时，熔池上方等离子体沿熔池切线向焊道凹面底部运动，使电弧温度场低温区范围增大。

4) 窄间隙焊接时，电弧受侧壁影响明显，利用传统的电弧热源及电弧压力等经验方程，对窄间隙电弧焊接过程进行数值计算时，需要对方程进行修正。