双液滴同时撞击粗糙多孔介质表面的数值模拟

邓辉良， 李培超

(上海工程技术大学 机械与汽车工程学院， 上海 201620)

液体在固体表面的扩散是一种常见的现象，且在工农业生产中都有很多应用，如农药喷洒、喷墨打印和雨滴撞击等[1-2]。大多数研究针对的是均匀光滑表面上的扩散[3-5]。然而，绝大多数真实的固体表面在不同程度上都是粗糙的，而且在许多情况下液滴撞击的壁面是粗糙多孔表面。由于液滴撞击的壁面的粗糙度和多孔性的存在，液滴撞击时除了铺展还会渗透，对于这种状况的研究，很多研究者也通过了实验和数值模拟的方法来分析液滴动力学行为。

Chandra等[6]2377-2388采用单镜头闪光摄影法对液滴撞击多孔陶瓷表面的变形和扩散进行了摄影记录，研究发现在相同温度下，多孔介质表面扩散的液体直径的最大值小于不渗透表面。Lembach等[7]研究液滴在电纺聚合物纳米纤维垫上跌落冲击的特性，在较高的撞击速度下，观察到微小水滴形成而且迅速飞溅；此外，还阐明了液滴在可润湿性纳米纤维垫跌落冲击后的渗透和扩散情况。Arshadi等[8]利用两相油/盐水溶液流入一个润湿、破碎的砂岩样品，通过改变溶液流量、裂缝孔径和流体之间的界面张力，阐明了在自吸过程中基质和裂缝区域的主要流动机制和优先流动路径。Lee等[9]对液滴撞击多孔结石的铺展和吸收进行了实验研究和数值分析，研究发现液滴的扩散和吸收大小取决于液滴的冲击速度，而后期岩石的含水量再分布则不太依赖于冲击条件。由于实验在多孔介质内部观察的局限性，所以很多研究者也通过数值模拟的方法来分析液滴在多孔介质上铺展渗透的动力学行为。Espin等[10]465以润滑理论模型为框架，推导出液滴在考虑多孔基底表面粗糙度情况下铺展和吸收的数学模型，并进行了数值模拟，研究了渗透率和粗糙度对轴对称液滴扩展的影响。Choi等[11]通过Leve Set法对液滴在多孔表面的蒸发进行了数值分析，将追踪液滴形变的Leve Set公式进行扩展，研究了传热和传质、孔隙率、多孔阻力及毛细管力对液滴的影响。Fu等[12]2948利用流体体积(volume of fluid,VOF)法来精确地跟踪液滴的变形，并结合压力隐式分裂算子(pressure implicit split operator, PISO)算法详细研究了液滴特性、多孔介质特性和液体与多孔介质润湿性对附着滴铺展和渗透的影响。Suo等[13]通过格子玻尔兹曼模型(lattice Boltzmann method, LBM)和孔隙网络模型(pore network method, PNM)结合的方法，建立了一个高效、稳健的数值框架，并通过实验验证了此数值框架在平坦多孔表面的正确性；此外，通过改变多孔介质表面的几何形状，证明了铺展和渗透是竞争关系。

由于上述研究基本上是针对单液滴撞击多孔介质表面的研究，而针对双液滴同时撞击粗糙多孔介质表面的研究较少，且粗糙度在很大程度上影响液滴在多孔介质铺展渗透[10]466，[14]。课题组在Fu等[12]2918-2919数值模拟的基础上，对双液滴同时撞击粗糙多孔介质表面时的液滴特性及其多孔介质特性进行了研究。本研究为实际工程应用中液滴撞击多孔介质问题提供有益的参考。

1 数学模型

1.1 问题描述

多孔介质表面不同于光滑的玻璃表面，多孔介质由于孔隙和颗粒介质以及加工制备等因素的存在，表面必定呈凹凸不平状。基于粗糙度的定义和前人用凹凸槽来表征表面粗糙度的数值模拟[15-16]，我们在Fu[12]2918-2919原数学算法的基础上，在多孔介质表面增加凹凸槽来代表粗糙表面建立模型。

1.2 模型建立

液滴撞击多孔基底的表面，可以简化为图1(a)所示的轴对称形式，其中虚线区域为计算区域。图1(a)中，x轴是空气与多孔介质层的交界面，上方为空气介质，下方为多孔介质，y轴为对称轴。假设液滴为球形，两个液滴的水平间距为S。图1(b)所示为液滴铺展渗透的局部示意图，其中凸台宽度为a，凹槽宽度为b，高度为c。

图1 双液滴的物理模型和铺展渗透中的局部示意图Figure 1 Physical model of double droplets and partial schematic diagram of spreading and penetration

2 模型验证

R*=R/r0；

T*=T·v0/r0。

式中：R为液滴铺展半径;Th是基板外部液体膜的厚度;T是时间。

图与时间T*的关系Figure 2 Relationship between and T*

由图2可知，课题组利用凹凸槽及所建立的模型可以模拟双液滴撞击多孔介质表面的运动过程，并且与前人的实验结果吻合的很好。

3 参数分析

课题组主要研究液滴韦伯数We、液滴水平间距S、平衡接触角θeq、多孔介质特性及其表面粗糙度对液滴在多孔介质上的动力学行为的影响。我们定义液滴铺展长度为l，射流高度为h。不同物性参数对液滴动力学行为的影响可以由下面几个重要的无量纲参数来描述：

1) 韦伯数We表示流体所受惯性力和表面张力之比，且

(1)

式中：ρ是液滴密度；v0是液滴初始速度;r0是液滴初始半径;σ为表面张力。

We增大时，表示惯性力起主导作用，即液滴越易变形。

2) 达西数Da表示多孔介质的渗透性，且

(2)

式中K表示多孔介质的渗透率。

计算中所取初始参数如下：液滴初始半径r0=1 mm;气液界面张力σ=72.8×10-3N/m;平衡接触角θeq=60°；孔隙度Φ=0.55；多孔介质颗粒直径dp=0.1 mm;多孔介质表面凹凸槽a=b=c=20 μm，液滴水平间距S=3 mm。

图3 不同韦伯数下双液滴形态变化Figure 3 Changes of double droplet morphology under different Weber numbers

3.1 韦伯数We的影响

图3所示为双液滴分别以We=13.9和346.6同时撞击表面粗糙的多孔介质的形态变化。韦伯数的大小表示惯性对表面张力效应的重要程度。由公式(1)可知，当液滴半径一定时，撞击速度越大，韦伯数越大。由图3可以看出，在2液滴撞击相遇后会形成射流液柱，这与文献[17]的4页和5页研究的现象类似。当液滴的韦伯数为13.9时，惯性力较小, 液滴撞击多孔介质表面后在水平方向的铺展速度较小；另一方面受多孔介质表面粗糙度的影响，铺展过程中动量损失大，导致液滴中心射流动能较小，形成一个较稳定的液柱。液柱逐渐变粗增高，在3.7 ms时达到最高, 随后开始降低。当液滴的韦伯数为 346.6时，2液滴合并的时间明显比前者快，由于液滴撞击的惯性力增大，两液滴迅速合并，并产生射流液柱，且在0.22 ms时,射流液柱顶部液体开始克服重力和黏力的作用，形成二次液滴。在横向上，在0.46 ms时，液滴克服表面张力的作用，形成伞状飞溅的二次液滴。此后随着时间的增加，产生的二次液滴越来越多，飞溅高度和宽度都在增加。

双液滴在多孔介质表面铺展渗透的过程中，韦伯数越大，铺展半径越大，射流高度越高，2液滴合并的时间越短。当韦伯数达到一定值时，液滴铺展边缘处由于液体没有及时渗入到多孔介质中，且冲击所受惯性克服多孔介质表面张力，所以液体在边缘处会产生多个伞状飞溅的二次液滴。在纵向上，2液滴在中心区域，相互挤压，在惯性的作用下继续往上，到一定高度时顶层液体的惯性克服表面张力与重力，随后液柱断裂，产生多个二次液滴。

3.2 液滴水平间距S的影响

双液滴的水平间距S在一定程度上会影响液滴合并的时间，从而影响2液滴合并后形成的射流液柱高度及铺展长度。图4所示为水平间距S=2.5，3.0,3.5 mm时，双液滴同时撞击粗糙多孔介质表面的流动形态变化过程。图5所示为双液滴合并后形成的射流液柱高度及铺展长度随时间的变化曲线。由图4可知，随着液滴水平间距S增大，2液滴合并所需要的时间就越长，合并后形成的射流液柱高度变低，但铺展长度不断增大，合并中心处，渗透深度减小。因此，为了提高表面涂层的质量，建议均匀喷涂液滴，液滴距离应适中。

图4 不同水平间距下双液滴形态变化Figure 4 Changes of double droplet morphology under different horizontal spacing

图5 不同水平间距下射流高度和铺展长度随时间的变化Figure 5 Changes of jet height and spreading length with time under different horizontal spacing

3.3 平衡接触角θeq的影响

图6所示为双液滴在平衡接触角为30°和120°时随时间的形态变化。当平衡接触角为30°时，液滴撞击的多孔介质表面为亲水壁面，液滴的铺展长度较大，射流高度增加。其原因是当平衡接触角较小时，润湿性较好，有利于液体在多孔介质表面的扩散。当接触角为120°时，液滴撞击的多孔介质表面为疏水壁面，所以液滴铺展长度较小，后期观察到环状回缩，射流高度在增加。液滴在4.8 ms时水平铺展的两端有大量液体堆积，形成一个类环状结构，这与梁超等[18]2748研究单液滴撞击不同浸润性壁面的结果吻合。随后边界液滴开始回缩，在中心处有大量液滴堆积。

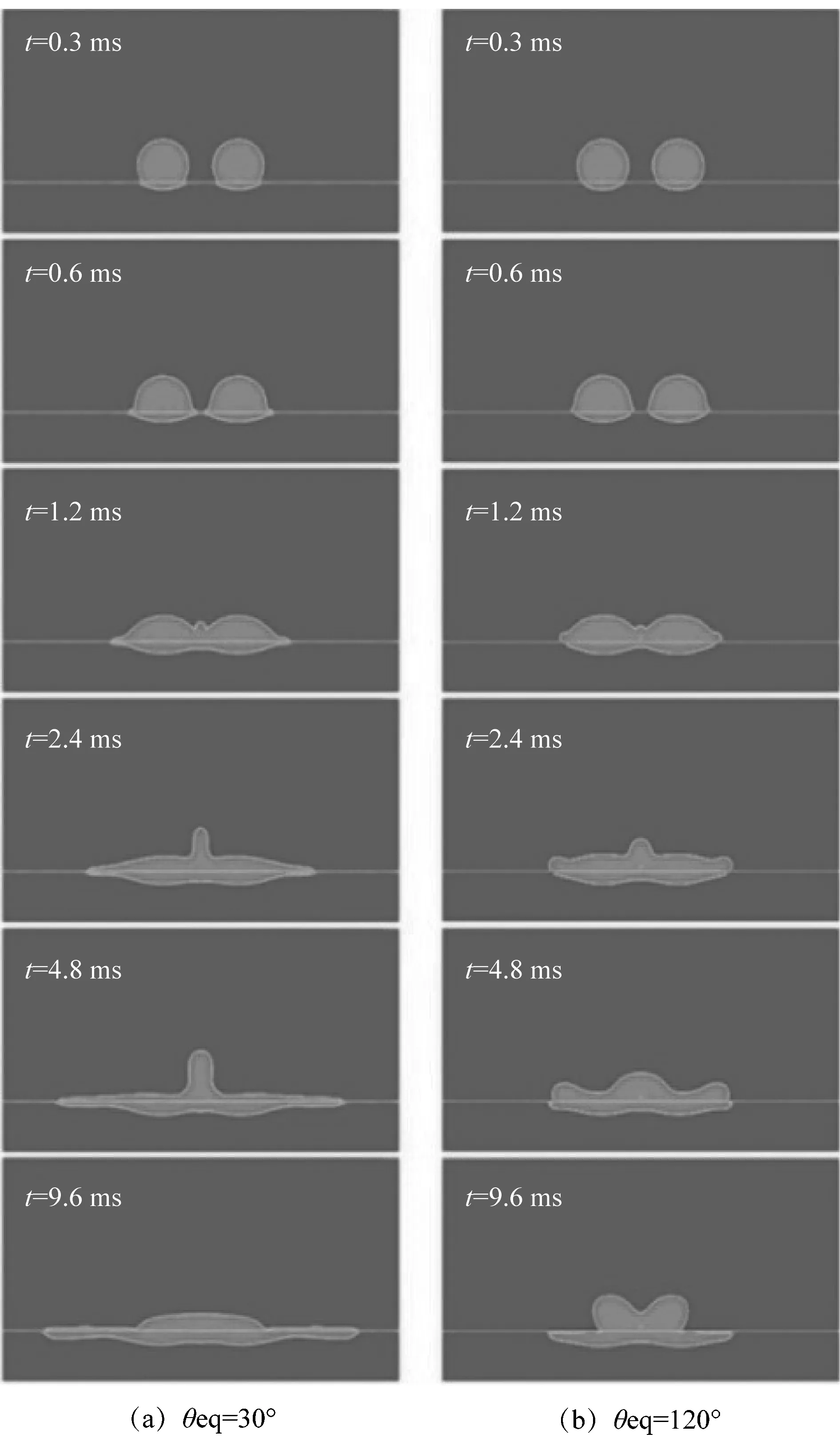
图6 不同平衡接触角下双液滴形态变化Figure 6 Changes of double droplet morphology under different equilibrium contact angles

3.4 达西数Da的影响

由公式(2)可知，当液滴半径一定时，达西数越大，多孔介质的渗透率越大；渗透率越大，液滴越容易渗透进多孔介质内部。铺展和渗透过程总体符合质量守恒，液体渗透进多孔介质后，停留在多孔介质表面的体积就越少，液滴的铺展半径就越小。

图7 不同达西数下射流高度和铺展长度随时间的变化Figure 7 Changes of jet height and spread length with time under different Darcy numbers

由图7(a)可以看出,达西数越大,双液滴合并后形成的射流高度越低,达到最大射流高度的时间越短。当达西数为8.5×10-7时,双液滴在5.0 ms达到最大射流高度，而达西数为8.5×10-4时,双液滴在2.5 ms达到最大射流高度。在这2种情况下,液滴的初速度均为1.0 m/s,惯性力相同，达西数越大,渗透率越大,多孔介质中固体基质对液滴的阻力越小,因此更多的液体渗透进多孔介质中,液滴停留在多孔介质表面的体积较小。形成的液柱就较短,达到最大射流高度的时间也越低。反之,达西数越小,同一时刻,液滴在多孔介质表面的体积越大，此时2液滴合并后形成的液柱较为细长,达到最大射流高度的时间增长。

图7(b)表示2液滴在多孔介质表面的铺展长度随时间的变化。当达西数为8.5×10-5时，在5.0 ms左右液滴铺展有回缩的趋势；而达西数为8.5×10-7时,液滴铺展最大长度趋于稳定。但达西数为8.5×10-4时,曲线在3.0～3.5 ms左右出现急剧下降，这是因为达西数较大,液滴很容易渗透进多孔介质内部,边界上的液体很快进入到多孔介质内部，因此铺展长度急剧减小。而中间堆积液体由于有向上的动能，渗透相对较慢，所以铺展长度在后期缓慢减小。

3.5 微结构表面粗糙度的影响

表1所示为不同多孔介质表面的沟槽结构。多孔介质表面上的粗糙度在一定程度上会影响液滴合并的时间，从而影响2液滴合并后形成的射流液柱高度及铺展长度。根据王宝和等[19]26的研究，凸台高度c越大，对应的粗糙度越大。如图8所示,当粗糙度增大时，2液滴合并所需要的时间就越长，合并后形成的射流液柱高度变低，铺展长度减小。由于粗糙度的增大，液滴在合并前动能损失较大，铺展长度和射流高度都减小。液滴铺展后期，在铺展边缘处出现回缩现象，且粗糙度越大这种回缩现象越明显。这是由于液滴铺展过程中，远端的液体动能逐渐减小，随着粗糙度的增大远端液体在多孔介质表面堆积就越多，一方面不足以提供向外继续铺展的动能;另一方面由于前面铺展的润湿性，液体与液体之间在表面张力作用下会回缩，同时液滴又在继续渗透到多孔介质中。

表1 不同多孔介质粗糙面

图8 不同粗糙度下射流高度和铺展长度随时间的变化Figure 8 Changes of jet height and spreading length with time under different roughness

4 结论

课题组采用ANSYS FLUENT对双液滴同时撞击粗糙多孔介质表面的流体力学进行了数值模拟。讨论了韦伯数、水平间距、平衡接触角和多孔介质特性及其表面粗糙度对射流高度和铺展长度的影响。得出如下结论：

1) 韦伯数越大，铺展半径越大，射流高度越高，2液滴合并的时间越短。当韦伯数达到一定值时，液体在边缘处会产生多个伞状飞溅的二次液滴。在纵向上，2液滴在中心区域，相互挤压，到一定高度时液柱会发生断裂，产生多个二次液滴。

2) 双液滴的水平间距越大，液滴合并所需要时间越长。合并后形成的射流高度越低，液滴在多孔介质表面的铺展长度越大，合并中心处，渗透深度减小。

3) 平衡接触角较大时，射流高度和铺展长度都减小，两端会聚集大量的液体形成环状结构。且随着平衡接触角的增大，边缘处的液体在张力的作用下会发生回缩现象，射流高度在后期阶段出现反弹现象。

4) 达西数越小，双液滴合并后形成的射流液柱越高，达到最大射流高度的时间越长。同时，液滴在多孔介质表面的铺展长度越大。另外，当达西数较大时，铺展长度有一段会急剧下降，然后与中间射流铺展的液体相遇又有小段升高，然后缓慢下降。

5) 粗糙度越大，2液滴合并所需要的时间就越长，合并后形成的射流液柱高度变低，铺展长度变小。