海潮负荷对大连地震台重力固体潮的影响
2021-07-03翟丽娜王松阳孔祥瑞
翟丽娜 王松阳 孔祥瑞
(中国沈阳110034 辽宁省地震局)
海潮是海洋表面受到太阳和月亮引力后产生的周期性涨落现象,与重力固体潮具有同源性,会产生相同的频谱特征,因此,在重力固体潮观测资料中会夹杂海潮信息(张邵栋等,1989)。分析重力固体潮汐残差信号可以获得地球内部动力学信息,但其中夹杂的全球和局部海潮负荷对重力固体潮影响较大,仅采用滤波法难以剔除,尤其在沿海地区,海潮负荷在重力潮汐振幅中占比更大(杜文成等,2018)。为了更加有效地利用已知重力资料精密测定地球潮汐常数等地球物理学参数,研究地核运动等地球动力学问题,有必要对重力观测资料进行海潮负荷信号改正(孙和平等,2002)。
Farrell(1972)首次提出采用海潮潮高和负荷格林函数进行褶积积分,求取海潮负荷影响;Schwiderski(1980)采用流体动力学差值方法构建较高精度的SCW80 海潮模型,被广泛认可并作为标准使用。伴随着现代高精度Topex/Poseidon(T/P)卫星测高技术的发展,结合地域特点,学者们提出多种高精度海潮模型(Sun,1992;Neumeyer et al,2005;Bos et al,2005;周江存等,2005,2007,2008;孙和平等,2005,2006;Florsch et al,2009;Arnoso et al,2011;Kim et al,2011;Kim and Shibuya,2013;Zhou et al,2013;徐建桥等,2014;Ducarme et al,2014;刘清超等,2016;杨锦玲等,2016;杜文成等,2018;翟丽娜等,2020)。辽宁省大连市国家基准台(下文简称大连台)是距海岸线较近的重力观测台站之一,海潮对重力固体潮观测资料的影响较大。文中搜集了现阶段应用较广泛的8 个海潮模 型:FES2004、GOT4.7、EOT11a、DTU10、NAO99b、HAMTIDE11a、TPXO72atlas 和TPXO72,对大连基准地震台重力固体潮受到的海潮负荷影响进行分析。
根据Farrell 等(1972)提出的理论,结合Agnew(1997)的积分格林函数计算法,将海潮与重力格林函数做褶积积分计算(刘清超等,2016;杨锦玲等,2016;杜文成等,2018),具体计算公式为
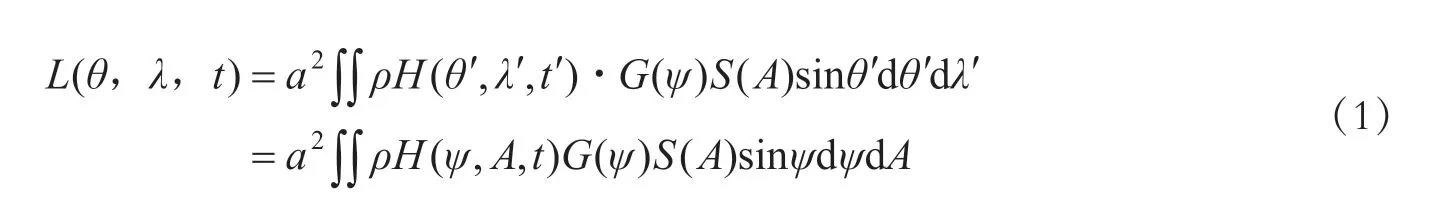
其中,L(θ,λ,t)表示某时刻某点的海潮负荷量,θ和λ分别为计算点坐标,t为时间;ρ为海水密度;a为地球半径;H(θ′,λ′,t′)为负荷点(θ′,λ′)处的瞬时潮高;G(ψ)表示与角距相关的重力负荷格林函数(该函数与负荷勒夫数相关)。
gPhone 型连续重力观测仪置于观测山洞,为了更加真实反映海潮影响程度,剔除重力干扰数据,估算重力固体潮各个波群的潮汐参数及精度,选取适合大连地区的8 个海潮模 型(FES2004、GOT4.7、EOT11a、DTU10、NAO99b、HAMTIDE11a、TPXO72atlas 和TPXO72),对主要潮波S2、M2、K2、N2、K1、O1、Q1和P1进行海潮负荷改正计算,对负荷改正效果进行综合评价,发现3 个主潮波的残差负荷改正有效性为43%—53%,其中对于K1波和O1波,TPXO7.2atlas 模型海潮改正效果最好,对于M2波,TPXO7.2 模型潮波改正效果最好(图1)。
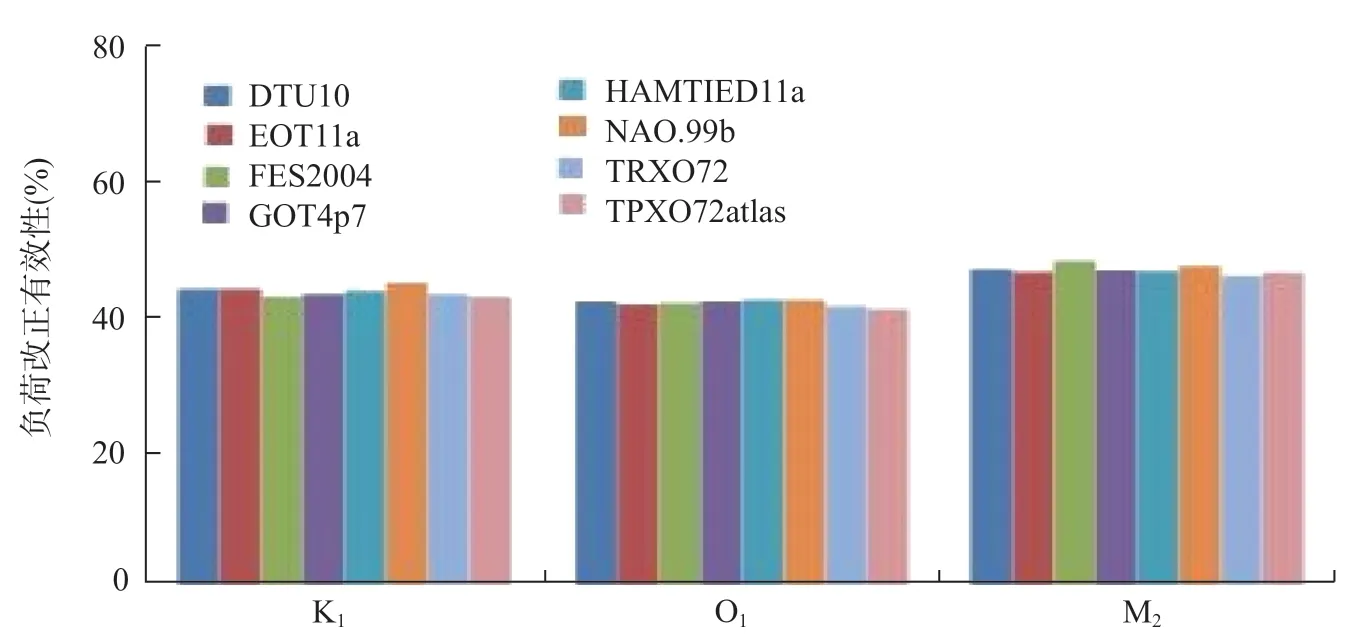
图1 K1、O1和M2波海潮负荷改正有效性Fig.1 Effectiveness of K1,O1and M2wave sea tide loading correction
总体来说,采用不同模型,主潮波的剩余残差值仍较大,可能与大连海湾位置的特殊性有关,近海模型存在误差,若采用近海高精度海潮模型进行修正,并在预处理方法中尝试改进,可能有助于计算效果的提升。
