点支式玻璃幕墙面板受力情况的思考

2021-07-03程杰

建材与装饰 2021年19期

程杰

（重庆创洲建筑装饰工程有限公司，重庆 400000）

0 引言

我国现阶段在对玻璃幕墙的应用设计中大多采取主体支撑结构与外围护结构非耦合的设计方案，这种设计路的巧妙之处在于可以独立地对玻璃面板进行受力情况的分析，而不必考虑到外围护结构对于主体支撑结构的限制和影响。基于此，还可以借助有限元的薄板理论对玻璃面板的受力情况进行模拟分析。

1 理论分析

1.1 基本假设

在实际的建筑工程中我们通常会把那些长度、宽度远远大于其厚度的构件称之为薄板，并将薄板内能够将其厚度均分的平面称为中面。在对玻璃面板进行受力情况的分析时一般进行弯曲力和薄膜力的分析，其中薄膜力主要包括作用在平面上的压力、拉力、剪切力等，而弯曲力则可以划分为弯矩、扭矩以及横向的剪切力。薄膜力可以导致玻璃面板发生一定程度的形变，而弯曲力则可以让玻璃面板在一定范围内出现弯曲。对于薄板而言使其发生小挠度的弯曲需要具备以下三个前提：

（1）假设垂直于中面的正应变以及正应力已经小到可以忽略不计时，并且如果此时在薄板内同一厚度的挠度、应变等均相等，可以得到式（1）：

基于上述公式我们可以得出，在薄板中面的任何一根法线处，各个点都具有相同的挠度，也就是说其挠度与所处的坐标Z无任何关联，只是X、Y的关联函数。

（2）我们假设应力分量引起的薄板变形τzx和τzy可以忽略不计，也就是说当薄板发生一定程度的弯曲时中面的法线长度是不会发生变化的，并且可以作为弹性曲面的法线。那么基于这一假设我们就可以得出rzx=0，τzy=0，根据相关的几何方程可以得出式（2）：

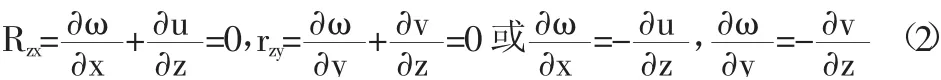
基于上述两个基本假设，我们可以得出薄板在发生小挠度弯曲时的物理方程，即：

通过观察这一物理方程我们不难发现，薄板的小挠度弯曲和平面应力都对应着同一个物理方程。

（3）我们假设薄板中的各个点均沿垂直于中面法线的方向发生运动，则平行于中面的位移或位移分量可用式（4）、式（5）表示：

通过式（4）、式（5）我们可以看出，即使中面的某一部分发生弯曲成为弹性曲面，它在xy平面内投影的形状仍然保持原有的形态而不会发生变化。

1.2 薄板弯曲的位移和应变

我们可以借助位移法对薄板的小挠度弯曲问题进行求解，其中我们可以将薄板的ω作为求解的最基本函数，那么我们可以根据式（1）对Z进行积分，最终得到式（6）：

最终可以得出式（7）：

我们利用挠度表示相关的应变分量可以得出式（8）：

1.3 薄板弯曲的应力与内力

我们基于式（3）和式（5）可以得出用挠度ω所表示的应力为：

通过式（9）我们可以看出σx、σy、τxy和坐标Z成正比关系，并且在薄板的上下表面处应力最大。我们在薄板内取出一个微元体，其应力分量的合成矩为：

我们将式（9）中的σx代入并对Z积分可以得到式（11）：

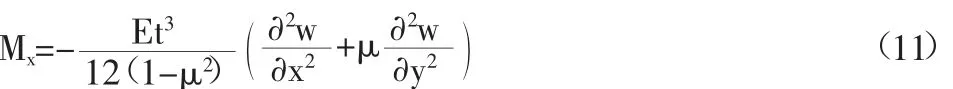
基于式（10）我们可以最终计算出薄板的弯曲刚度D为：

其中：t-薄板的厚度；μ-泊板比。

1.4 平衡方程

薄板的平衡受力分析图如图1所示。

图1 薄板平衡受力分析

由Σx=0；Σy=0；ΣMz=0得：

消除其中的dxdy并且忽略掉高阶微量后可以得到：

将式（14）代入式（15）中，然后根据Mxy=Myx可以得出由弯矩、扭矩、荷载所表示的平衡方程：

我们根据拉普拉斯算子可以将式（16）最终化简为DVω4=q。

2 工程实例

2.1 工程概况

某地区的一高层建筑需要应用外围玻璃幕墙结构，在本文中充分考虑玻璃幕墙在所处地理环境下所承受的风荷载以及水平地震荷载的作用，我们以中空玻璃为例，其所承受的风荷载标准值可以根据式（17）、式（18）将风荷载分配到内外两层玻璃上：

平行于玻璃幕墙平面的水平地震荷载可以基于式（19）进行计算：

我们将本工程中所测定的参数代入上述公式后最终计算得出在风荷载和水平地震荷载的共同作用下玻璃幕墙所能承受荷载的设计值为0.97kN·m-2。

2.2 模型的建立与分析

我们基于工程概况可以对玻璃幕墙建立有限元分析模型，其中玻璃面板借助壳单元进行模拟分析，需要特别指出的是在进行有限元分析的过程中需要考虑到由于剪切变形而产生的影响。其中点支式玻璃幕墙的材料属性按照表1所示内容进行输入，而点支式玻璃幕墙在风荷载以及水平地震荷载的综合作用下所能承受的最大、最小应力等值线示意图如图2所示。

表1 点支式玻璃材料属性

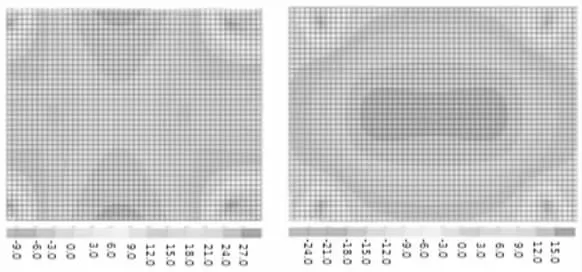
图2 点支式玻璃幕墙所能承受的最大应力（左）和最小应力（右）

众所周知，玻璃作为一种脆度很高的材料很容易因为拉应力在表面产生裂痕而导致最终破裂，根据某些专业结构的调查数据显示，一块玻璃自受到荷载开始直至玻璃发生破裂的过程中，玻璃面板的应力-应变关系几乎都呈现出线性关系。在此情况下我们需要借助最大拉应力理论对玻璃面板的强度进行计算和校验。通过获取的最大应力示意图不难发现点支式玻璃面板均会在支撑处出现压应力，并且可以发现玻璃面板所承受的最大拉应力会沿着横向的对称轴对称分布，并且呈现出由面板中心逐步向两边减小的趋势，其中最大拉应力出现在玻璃中心两侧的边缘处，将其最大拉应力与标准设计值进行比较后可以得出这一玻璃面板的强度是符合工程建设规范的。

通过分析此次工程建设中玻璃幕墙的主拉压应力的轨迹分布图我们不难发现点支式玻璃幕墙的应力分布在支撑处呈现出不均匀的态势，其应力迹线呈现出杂乱无章、曲折无序的样貌，并且在各支撑点处的应分分布极广。这一现象说明在支撑点处的应力相对集中，也就是说点支式玻璃幕墙的各支撑点处是相对薄弱的地方，相对而言比较容易被破坏。