质心动能定理与相对动能定理
2021-07-03汤幼强
汤幼强
(南昌县莲塘第一中学 江西 南昌 330200)
黄亦斌
(江西师范大学物理与通信电子学院 江西 南昌 330022)
1 理论
质点系的动能定理其实不止一种,正如质点系角动量定理可以对静点,亦可对质心,不止一种一样.我们先来梳理一下质点系动力学.
对于一个一般的质点系,可以对其中每个质点列出质点动力学方程(动能定理、动量定理和角动量定理),其中每个方程的左边涉及到力(包括内力和外力),而右边则涉及对运动的描述(动能、动量和角动量).将这些方程相加,左边就是内力和外力的贡献,右边则出现系统的总动能、总动量或总角动量.
下面是牛顿第三定律上场.这个定律似乎存在感不强,其实相当重要.正是由于这个定律,使得一对内力的冲量之和为零,力矩之和为零.这就使得质点系的动量定理和角动量定理的左边不出现内力,只有外力.多大的简化!遗憾的是,一对内力的做功问题要复杂.由牛顿第三定律,一对内力做功之和不一定为零,但也简单到仅依赖于两相互作用质点的距离变化.于是有质点系动能定理:外力功和内力功之和等于系统动能的变化
(1)
A内+A外=dK
接下来,我们进入力学量的分解.对任意质点系都可以定义质心,注意这里没有任何前提条件.质心是质点系的平均位置,是各质点以质量为权的加权平均位置
(2)
由此自然引申出质点系的平均速度——质心速度和质点系的平均加速度——质心加速度
(3)
显然,质心运动代表着质点系的整体运动.此外,每个质点还存在对质心的相对运动
ri=rC+r′ivi=vC+v′iai=aC+a′i
(4)
质心运动和相对运动有时又称为外部运动和内部运动,在刚体情况下也称为平动和转动,或公转(轨道运动)和自转(自旋运动).
我们知道,对于一般的质点系,利用速度分解式(4),可以得到动能分解的柯尼希定理
(5)
K=KC+K′
恰好是式(1)右边的分解,其中右边两项分别是质心动能和相对动能,在刚体情形又分别叫做平动动能和转动动能.左边是不是也可以分解呢?定义了质心后,质点系动量定理等价于质点系质心运动定理
(6)
其中左边只有外力,没有内力.将上式两边点乘质心位移drC,可得到
(7)
此式右边是质心动能的增量,故这就是质心动能定理.在这个定理中,内力根本不出现,而各外力所点乘的位移并不是式(1)中各自受力点的位移,而是统一为质心位移.式(1)中左边的外力功又可依式(4)变为
(8)
此式可理解为外力功的分解.联立式(1)、(5)和(7),马上得到相对动能定理
(9)
其中外力点乘的位移是各自受力点相对于质心的位移,而内力功部分的位移仍为两质点间的相对位移:dr′ji=drji.相对位移与惯性系还是质心系无关.
以上内容可以总结如下
(10)
其中,3个横式分别为质点系的(总)动能定理、质心动能(平动动能)定理和相对动能(转动动能)定理,3个竖式分别为内力功、外力功和动能的分解式.可以看出,每个外力功可分解为质心运动部分和相对运动部分,而内力功则只有相对部分,这是因为内力不会影响质心速度和整体运动.
作为对比,我们看看对角动量定理的分解.对静点的质点系角动量定理为
(11)
其中,右边存在角动量分解(类似于动能的柯尼希定理)
(12)
两项分别为质心角动量(将整个系统的质量集中于质心后对静点的角动量)和相对(于质心的)角动量.而左边的合力矩可依式(4)分解为
(13)
式(12)、(13)中,左边是对应的[见式(11)],右边第二项也是对应的(即对质心的角动量定理),故有如下表示

(14)
其中,3个横式分别为质点系的(总)角动量定理、质心角动量(轨道角动量)定理和相对角动量(自转角动量)定理,两个竖式分别为力矩和角动量的分解式.与式(10)不同的是,此处没有内力项.
2 例题
以常见的一道柔链题为例[1]进行分析.题目如下:
一柔链条长为L,单位长度的质量为λ,链条放在有一小孔的桌面上,一端由小孔稍伸下来,其余部分堆在小孔周围,如图1所示.由于某种扰动,链条因自身重量开始下落.求链条下落速度与落下距离之间的关系.所有摩擦不计.
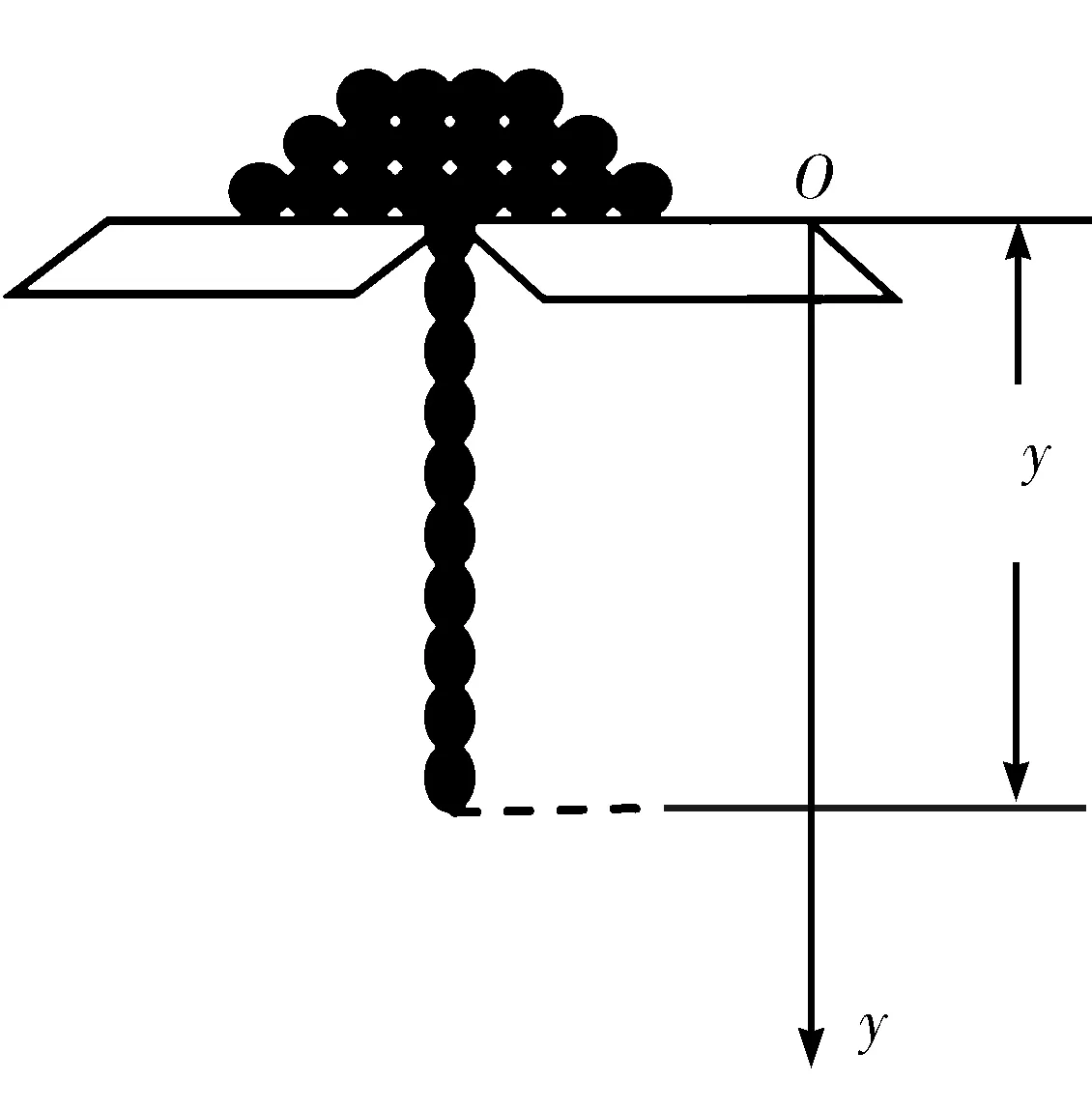
图1 柔链放置图
可以看出,由于存在完全非弹性碰撞(上部的静止链条被下部的运动链条突然拉扯),此系统机械能不守恒.文献[1]给出多种方法,此处用质心动能定理求解.
质心动能定理中的功是“质心功”,有两个要素:一是只有外力,没有内力;二是位移只是质心位移.此题中的外力是支持力和重力,其中支持力做(总)功为零,但其质心功为负(质心下移);重力当然包括上部的重力和下部的重力,然后还要乘以(整个系统的)质心位移,故都做正功.
此题的关键是要确认:系统所受外力之和等于下部的重力.考虑一微元过程:上部相接处的一小段链条被下部拖动.此过程中,该小段与上部之间并无相互作用,只存在该小段与下部之间的拉扯,故上部所受的支持力除了抵消上部的重力外无额外的部分.于是,支持力与上部重力之和为零,二者的质心功之和为零,只剩下下部重力的质心功——下部重力(λyg)乘以整个系统质心的位移(dyC).于是,根据质心动能定理,有
(15)
容易计算出
代入式(15),化简即得

文献[1]对此题进行了详尽的分析,给出多种解法以及一些概念辨析.可以看出,本文上述解法实质上就是文献[1]的解法三,只不过该解法在那里被误判了.
