科学问题问题域、应答域的难度系数集消解途径研究

沈振东

科学哲学是从哲学的角度考察科学的一门学科。它以科学活动和科学理论为研究对象，但以往的科学哲学以及科学哲学家们主要探讨后者，即对科学的本质、科学知识的获得和检验以及科学理论的逻辑结构等有关科学认识论和科学方法论方面的基本问题的探讨，而很少研究如何提出科学问题、科学问题的结构以及科学问题自身的演化机制等。对科学问题的研究也应该属于科学活动本身的应有之范畴。本文不拟对科学问题的所有相关的方面全面展开研究，而只专注于研究科学问题的难度指标及科学问题的难度评价。

美国认知科学家，诺贝尔经济学奖获得者H.A.西蒙曾经提出过这样的问题：“为什么有些问题容易，有些问题困难，即问题难度的基础是什么呢？”[1]但他并未能对此问题作出任何正面的回答。他似乎曾经设想过能否用问题的搜索空间的大小来估量问题的难度，因为似乎“问题的搜索空间越大，可能就越困难”[2]，但深思熟虑的西蒙马上否定了这种可能性。他回答说：“不能仅从表面上搜素空间的大小来判断问题的难度。有些问题看上去不大，可是很难解决。”[3]他举出了很多实例来说明他的这种回答的合理性。更何况，并非任何问题的搜索空间的大小都是可以计算的，乃至是可以作出数量上的比较的。事实上，问题的难度也很难用单一的一种指标来进行度量。我国学者林定夷先生也曾说过：“问题的难度很难作出真正客观意义上的评价，因为它与解题的思路甚至突然的顿悟都有关。但是，尽管如此，我们毕竟还是有可能对问题的难度作出相对客观的评价。影响问题难度的评价的主要因素有三个：问题的目标状态，问题的当前状态和能力。然而，如何真正地来掂量某个科学问题的难度，这实在又是与问题的细致的、合理的分解密切相关的。而如何细致的合理的分解又无法进行计算和量化。”[4]

从西蒙和林定夷两位学者关于科学问题难度的论述，我们不难看出，尽管对科学问题的难度作出客观的评价确实很难，但他们都提到了某种“域”的含义——西蒙提到的“搜索空间”，林定夷提到的“当前状态”和“目标状态”。本文中，笔者拟将定义两个概念“问题域”和“应答域”，并借用这两个概念以及对在科学活动中的某个科学问题的问题域和应答域的不断调整，而呈现出该科学问题的逐渐消解的过程，即科学问题的难度逐渐降低。

一、科学问题的逻辑构型

科学问题是指一定时代的科学家在特定的知识背景下提出的关于科学知识和科学实践中需要解决而尚未解决的问题。它包括一定的依据背景知识而确定的问题域、求解目标和应答域，但尚无确定的答案。

设W 表示科学认知主体CS（cognitive subject) 的已知世界，W 由三部分构成：CS 的背景知识BK(background knowledge）（包括CS 的经验事实和理论事实）、W 中的推理规则IR(inference rule)（主要指逻辑规则和数学规则），以及W 所遵循的范式PD(paradigm)（即CS 所接受的一组假说、理论、准则和方法的总和，包括特定的世界观、本体论和方法论等）。X 表示提问对象，X 的所有可分解成的原子成分在W 中都有意义，这是保证了X 在W 中的意义标准[5]，但X 的可解性可能超出了W 界限。Q 表示提问方式，根据问题的可归约性理论[6]，Q 可以归约为一般疑问句的形式，即“命题+？”形式。根据W 以及X 可以构造X 的所有可能的解Si（solution)(i=1，2，…，n)组成的解空间SS（set of solutions)，对于给定的W 和X 而言，SS 是有限集。

（一）常规问题RP(routine problem)可形式定义为

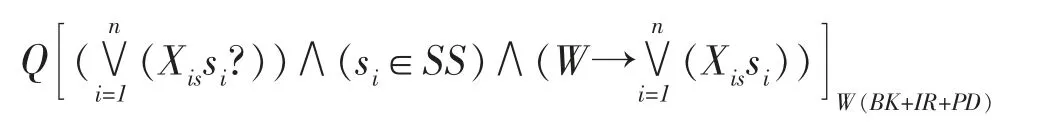
这里的X 和每个si在W 中都有意义，且每个命题“X is si”都是W 中的合法语句（这里的合法语句的含义可以加以定义）。定义中的表示n 个一般问题“X is si?”的析取，表示是W 的逻辑后乘。该定义意为，如果某个问题是常规问题，则根据认知主体的背景知识，可以构造问题的解的一个完全闭包集，并且根据W 的推理规则经过有限次的机械步骤或有限次的试错，最终可以在这个闭包集中成功地确定问题的解。常规问题的解在已知世界中都是逻辑确定的，即问题的解所在的集合是W 的逻辑闭包的。

从逻辑上而言，尽管常规问题都是可解的，但常规问题也存在难易之别，这里的难易度主要由所构造的问题的解的空间是否完备以及所使用的逻辑推理的计算次数多寡有关。常规问题主要存在于知识学习者那里，随着学习者的知识结构的逐渐完备以及推理能力的逐渐增强，常规问题一般都可以自行得以解答。这里所讨论的常规问题一般不是科学探究者（或曰科学家）所重点关注的问题，科学研究者更多地是关注下面所定义的科学问题。

（二）科学问题SP(science problem)可形式定义为[7]

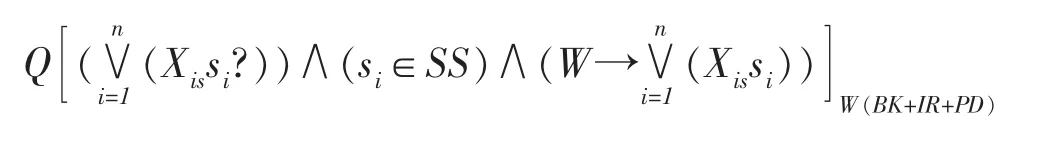
其一，由于W 中的背景知识BK 的不完备所致。例如，对于问题X={抛掷出一枚硬币着落后的结果是什么}，根据通常的背景知识BK，可构造出可能的解集={s1正面向上，s2=背面向上，s3=直立}。但是，当这枚硬币是由易碎的假材料制成的且这假材制成的硬币的信息还没有进入认知者的背景信念时，那么认知者的可能解集仍然应该是原来的解空间={s1正面向上，s2=背面向上，s3=站立}。但实际上，硬币落地时可能出现第四种结果“s4=粉碎”。尽管“粉粹”一词在认知者的背景知识中是有意义且“X=s4”是合法语句，但是认知者在构造X 的解集时是不会将硬币的着地与粉粹联系一起的，语句“X=s4”对于BK 而言是不可思议的。所以这种情形下的表示的含义是，由于背景知识的不完备，无法构造出所有可能的解所组成的解集。

其二，由于推理规则IR 的不完备所致。例如，科学史上关于光本质的论战的早期，当牛顿1675 年提出的“光的微粒说”（记作IR1），此时根据IR1，考察这样的问题：X={当一束光斜着射到两种介质分界面处时将会出现什么结果}，根据光的微粒说的原理，只能构造出可能的解的空间={s1=反射，s2=折射}。但到了1690 年，惠更斯提出“光的波动说”理论（记作IR2）时，那么对于上面同样的问题X，就可能构造出解答空间={s1=反射，s2=折射、s3=反射与折射同时发生、s4=光线交叉相遇后仍然不改变方向继续前进}，尽管s3和s4是合法语句且存在逻辑上的可能性，但对于IR1而言，s3和s4是不可理解的，所以不可能进入IR1推理规则决定下的解空间。对于同一个问题，为何会构造出两个不同的解的空间，主要原因就是在构造解的可能的空间时，探究者所依据的推理规则是不一样的，随着推理规则越来越完备，那么所构造出的解的空间就越完备，即科学问题的解属于解的空间的可能性就越大。

其三，由于一个研究纲领的不同的辅助性假说所致。根据拉卡托斯的研究纲领方法论，一个科学理论系统由两部分组成：中心是“硬核”（hard core，简记HC)，周围是“保护带”（protective tape，简记PT）。理论的研究纲领由硬核和保护带组成，即{HC+PT}，理论的研究纲领的不同主要是由不同HC 的决定的。当一个理论遭遇反驳或挑战时，首先作出的是对理论的PT 部分进行修改，以免HC 遭受冲击。例如，托勒密时期的天文学家就是通过修改或引进本轮和均轮等辅助性假说，以保护地心说免受冲击的。基于地心说的研究纲领而言，在本轮和均轮等辅助性假说修改前后可以设计同一个问题：X={行星绕地球的轨迹是什么}，根据HC={地心说}和辅助性假说PT1={行星绕着地球的轨迹是圆周形}，可以得出X 的解的空间={s1=行星绕着地球的轨迹是圆周}；而根据HC={地心说} 和辅助性假说PT2={行星的本轮和均轮的假说}，可以得出X 的可能的解的空间={s1=圆周运动，s2=非圆周的多样性变化}，s2在纲领：{HC+PT1}下不仅没有事实的可能甚至也没有逻辑的可能性，因此s2是不可能进入{HC+PT1}下的解的空间的，所以当被观察到的行星轨迹发生非圆周轨迹时是不可理解的，为了消解这个反常，修改了理论的保护带，以使得s2不仅是逻辑上的可能的，而且在事实也是合理的，这样在研究纲领：{HC+PT2}下，s2就进入了问题X 的解的空间了。[8]

其四，不同的理论范式PD 所致。看似同一个问题在不同的范式下，构造的解的空间有时不但不同，甚至是不可通约的。库恩曾经说过，“当范式改变时，世界本身也同它们一起改变。”所谓范式，在库恩看来，就是一种对本体论、认识论和方法论的基本承诺，是科学家集团所共同接受的一组假说、理论、准则和方法的总和，这些东西在心理上形成科学家的共同信念。按照范式理论，同一个科学问题，对于不同的科学家共同体根据各自的范式理论所能构造的解的空间不仅可以是不同的，甚至可以是相互冲突的。例如，化学史上关于物质燃烧的解释，有两种解释范式——燃素说和氧化说。按照燃素说，燃烧是一种分解过程，物质燃烧时释放出一种叫做“燃素”的东西；按照氧化说，燃烧是燃烧物与空气中的氧的化合过程。问题X={是什么原因导致金属燃烧后的重量增加的？}，根据燃素说，可以构造解集={金属在燃烧时，重量增加是因为燃素具有负重量}；根据氧化说，可以构造出解集={金属在燃烧时重量增加，是和空气中的氧气化合的结果}。显然，根据不同的范式，这个例子中所构造的解集之间不但是不同的，而且相互之间还是不相容的。从逻辑可能性的角度而言，不同的理论范式所构造的解集或所给出的解释，在各自的理论范式框架下可能都是合理的，不同的理论范式所提供的科学解释之间既可以是无法通约的，也可以是有优劣之分的。例如这里的例子，氧化说就比燃素说更进化，燃素说为了解释有的物质燃烧时重量变轻，有的物质燃烧时重量变重，必须引入更多的辅助性假说——有的燃素具有正的重量，有的燃素具有负的重量；而从简单性角度，相比较而言，氧化说在解释物质燃烧时不需要引入辅助性假说，同时氧化说不仅能够解释燃素说能够解释的所有问题，而且能够解释燃素说不能解释的一些新的问题，所以氧化说更先进。

其五，前几种情形的混合所致。

二、科学问题的问题域和应答域

我们知道，不论是科学问题还是哲学问题从来都不是抽象地存在着，而是存在于特定的问题域中。从上文关于产生科学问题的几种类型来看，所谓科学问题的问题域，简而言之，是指提问者基于自己的背景知识规定了问题的存在边界、关联问题之间的内在关系以及答案所可能分属的逻辑空间。

（一）科学问题的问题域

设PD（problem domain) 表示科学问题的问题域。

SB(scientific boundary)表示科学问题的边界。所谓问题的边界（也可称为类问题变成科学问题或有意义问题的存在的范围、幅度），意为对于某个问题而言，在其他要素都具备的条件下，只有规定了问题的边界该问题才有意义，否则该问题就无意义。换言之，科学问题的存在边界就是一个类问题变成真问题（科学问题、有意义问题）的意义边界。例如，对于类问题：“方程ax2+bx+c=0（a≠0）是否有解？”是没有意义的，而应该问“在某某范围内（例如实数范围内或复数范围内），方程ax2+bx+c=0（a≠0）是否有解？”才变得有意义。这里的“实数范围或复数范围”就是该类问题成为真问题（科学问题、有意义问题）的存在边界，离开这个边界抽象地谈论某个问题是没有意义的。科学问题的边界往往是由科学研究主体的背景知识决定的。

IR 表示关联问题之间的内在关系（即上文中的推理规则），这里的内在关系一般以逻辑关系为主。一般具有两种逻辑关系：第一，逻辑上的包含关系，可分为母问题和子问题。母问题可以看成是对子问题的合成，而各个子问题可以看成是对母问题的分解。一般而言，把一个母问题的所有子问题都解决了，则该母问题也就解决了。该种问题的逻辑关系具有下列逻辑构型：＜CP：SP1+SP2+…SPn＞，[9]这里的CP(complex problem)表示母问题，（simple problem）表示子问题。一个大型的、带有全局性的问题往往都是通过分解成各个子问题，并对这些子问题分别加以解答而最终得以解决的。例如，在美苏冷战时期的军备竞赛过程中，美国想实施代号为“阿波罗”的巨大空间探测计划问题，美国把这个在外人看来不可能解决的难题逐一分解成理论问题、工程技术问题、财政经费问题以及科研人员协调管理问题等四大子问题。应该说美国能够提前两年完美地实现登月成功，与把问题的周密而详细的分解有密切关系，正如后来的日本派科研团队考察这个登月设备和工艺时，不胜感慨到就技术而言，日本完全有能力造出，但就庞大的科研团队的协调和管理，日本是无能为力的。应该说，美国的登月成功在很大的程度上得益于把复杂的问题细化分解，然后集中优势力量攻克难关。第二 具有逻辑上的后乘关系，可以分为前问题PP(priority problem)和逻辑后乘问题LPP(logical posterior problem)。一个问题的意义真值有三个——有意义、无意义、真值悬置(有意义真值记为1，无意义真值记为-1，真值悬置记为0）[10]，前问题和逻辑后乘问题之间的逻辑关系可刻画为：（TR（LPP）=1）→（TR（PP）=1））∧（（（TR（PP）=0）∨（TR（PP）=-1））→TR（LPP）=-1 即LPP 是否有意义取决于PP 是否有意义。具体而言，当逻辑后乘问题是有意义的，则前问题一定有意义，且当前问题为假或真假悬置时，则后乘问题一定为假。

LS(logical space)逻辑空间，表示某个科学问题中的所有的“原子命题”[11]之间所遵循的不同逻辑函数关系组成的全部可能的逻辑函数。对于某个科学问题P 而言，令APS(atomic propositional set)表示问题P的所有的“原子命题”组成的集合，即APS={AP1，AP2，…，APn}，这里APi的表示原子命题；记命题与命题之间的所有可能的逻辑函数关系集为LFS(logical function set)，LFS={F1，F2，…Fn}这里的逻辑函数Fi可以是一元的或多元逻辑函数。设APSi⊆APS，LFSi⊆LFS（即APSi是APS 的子集，LFSi是LFS 的子集），当LFSi作用于APSi时，就可得到原子命题组成的现实世界所对应的一个映射的世界，即由现实世界对应的一个可能世界。如果用LFS 作用于APS 就可以得到根据所有原子命题所能映射到的所有可能世界的全集。理论上讲，这个全集就是某个科学问题的逻辑空间，即＜LS：APS+LFS＞。

则可以将科学问题的问题域形式表示为＜PD：SB+IR+LS＞。

科学问题的问题域PD 不同，看似是同一个问题，但其内涵不同，其解答的难度以及被解答的程度都有很大区别的。例如对于“遗传的本质是什么？”的问题，在孟德斯鸠的问题域中是“遗传因子”问题，在摩尔根的问题域中是“基因”问题，而在奥森和克里克的问题域中则成为DNA 分子的结构问题。这里的问题域的不同就导致对看似同一个问题，却给出了不同程度的回答。所有这些不同的解答都可以称得上是基于不同的问题域而对问题的解答。显然这里的从孟德斯鸠经摩尔根到奥森和克里克的回答存在着解答上的精准性和递进性问题。

（二）科学问题的应答域RD（Response domain of Scientific problems）

科学问题的应答域是指在问题的表述中对问题解的存在所作的预设，它蕴含着提问者所指示的求解方向和求解范围。如果我们把科学问题的问题域看作数学映射中的原象的话，那么科学问题的应答域就相当于数学映射中的象，即RD⊆LFS（P）。科学问题的应答域实则就是科学探究者根据问题域中的全部或部分推理规则作用于科学问题所得到的解空间的全集或其子集。从认知生成的规律角度而言，问题的解答者按照其背景知识往往一开始是预设一个最简单的、最直接的解的空间，然后再根据不断有新的背景知识的加入，从而使得问题的解空间的边界逐渐明晰。这个解空间变动的过程有两个结果——逐渐收缩型和逐渐扩展型。

科学问题解空间的收缩型。对于科学问题P 及逻辑空间LFS 的子集LFSi和LFSj，如果用这两个不同的子空间逻辑函数分别作用于科学问题P 可以得到不同的应答域LFSi（P）和LFSj（P），那么对于问题P的真正的解属于这两个应答域的交集的可能性一定是大于属于各自的应答域的，即很有可能属于上面两个解空间的交集，即LFSi（P）∧LFSj（P）中，这样就出现了应答域逐渐收缩的情形。所以，在实际的科学研究中，科学研究者往往会从不同的角度尝试地对某个科学问题解答，如果不同的科学方法对某个问题都给出相同的说明，那么这个结果成为科学问题的解的可能性就更大。例如，在医学治疗中讲究对症下药的原则。对于“病人出现某种症状的病源是什么”的问题，即对于疑似病例的诊断，一般会采取不同的诊疗手段或检测方法从不同的角度进行检测，以减低误诊率、提高准确性，从而最终确诊某种疾病。在目前医疗诊断中常常被同时采用的属于临床经验的案例推理和条件概论理论中的贝叶斯推理方法，就可以大大提高诊断的准确性，高度锁定病源。这里的案例推理方法就是从过去的经验中发现解决当前问题线索的方法。案例推理在处理问题时，先在案例库中搜索与目标案例具有相同属性的源案例，再通过案例的匹配情况进行调整。基于案例推理简化了知识获取的过程，对过去的求解过程的复用，提高了问题求解的效率，对有些难以通过推导来求解的问题，可以发挥很好的作用。与案例推理方法的不同，贝叶斯推理是建立在主观判断的基础上，先估计一个值，通过新获得的观察结果来不断更正对概率的判断，从而使得诊断结果越来越具有高确证性。即先预估一个先验概率，然后加入实验结果，看这个实验到底是增强还是削弱了先验概率，由此得到更接近事实的后验概率。如果在某个医学诊断中，通过案例推理和贝叶斯推理都得到关于某个症状的是由同一病源引起具有很高的相似度，那么很大程度上就可以确定这个病源就是该症状的解空间，即大概率情况是可以锁定某种症状的病源的。科学问题解空间的收缩型往往是对应于科学问题的背景知识相对清晰而推理规则存在多元化的情形，实际上，这种情形的科学问题的消解过程就是不断地采用新方法、新理论、新推理规则作用于科学问题的过程。

科学问题解空间的扩展型。对于科学问题P 及逻辑子空间LFS 的LFSi和LFSi+1，如果LFSi（P）⊆LFSi+1（P），则称解空间LFSi+1（P）是对LFSi（P）解空间的拓展。随着背景知识不断地加入，问题的解空间不断地完备。表面上讲，问题的解空间越大，对问题的解的确定可能就越困难，但实际上，并不一定如此。因为，从逻辑上而言，问题的解空间构造越完备，那么这个问题最终被消解的可能性就越大。实际上，这种情形的科学问题的消解过程就是不断地构造解空间的完备的过程。例如，对于问题“当下美国为什么会爆发世界上最严重的新冠疫情”的根本原因的分析。随着时间的变化，我们可以先后根据了解到越来越多的不同背景知识，构造出不同的解空间：如果从新冠肺炎疫情爆发开始，到2020 年3 月12 日，美国才宣布切断除了英国以外的所有国家的航班”为仅有的背景，则可构造RD1={美国关闭的边境行动比较迟缓}；如果进一步把“美国工人崇尚个人主义、自由主义，国家要求隔离的禁令可能被某些人违反”加入到背景知识的化，则可进一步构造RD2={美国关闭出入边境行动比较迟缓、美国是民主制国家}；如果进一步地把“2020 年11 月是美国总统大选之时，而且现任总统是否赢得总统连任的最最关键因素是经济领域的表现”并入背景知识的化，则可进一步地构造RD3={美国关闭出入边境的行动比较迟缓、美国是民主制国家、美国今年是大选年，经济是否改善是特朗普能否连任的重要筹码}……这里关于解空间不断扩大的动力机制是因为问题解答者不断地加入新的背景知识而所致。

应答域可以看作是问题域中的LFS 的某个子集作用于APS 的某个子集所得到的函数集合。应答域与问题域存在着密切的关联性，对于特定的科学共同体考察某个特定的科学问题而言，该科学问题的问题域是确定的，但其应答域却可以是动态变化的，即随着不断地科学问题的背景知识的不断介入，该科学问题的应答域不断越来越清晰、越来越确定，这种越来越确定的过程其实就是科学问题的难度降低的过程。

三、科学问题难度系数及科学问题的消解的动力学机制

从前文分析可以得出，如果说科学问题的问题域是界定问题是否可称为科学问题的意义标准，那么科学问题的应答域的确定实则就是一个问题由科学问题逐渐转化为常规问题的问题难度消解过程。直观上讲，科学问题难度的消解就是逐渐确定应答域（即解空间）的过程，可以从两方面降低问题的难度：

一是不断增加新方法以逐渐锁定应答域。根据科学问题解空间的收缩型情况，可以将该方法的逻辑结构形式表示为：设LFSi和LFSj是可以作用科学问题P 的两个逻辑函数，δ（·）表示难度系数，“A≺B”表示A 弱于B。若（LFSi⊆LFS）∧（LFSj⊆LFS）∧（（LFSi∧LFSj≠Φ），则

这里含义的直观解释就是，通过从不同的科学角度对同一个科学问题进行研究，可能获得不同程度的科学解答，那么根据这些不同科学方法得到的不同解空间的公共解就可能是该问题的最佳的解答。所以在现实的科学研究过程往往要求不同领域的专家从不同的理论角度给出某个问题的尝试的解答，然后再综合考量这些不同理论背景下的解答，从而最终逐渐减低该问题的难度。对于从不同的方法角度研究同一个科学问题时，往往可以使问题解决起来更加容易些。所以，随着国家发展战略的推进，需要不同领域的专家学者从不同的专业角度论证某个大型项目的可靠性及其可行性。学科的交叉研究、大学科群的兴起等等就是基于这个理念而产生的。

二是不断增加新背景知识以逐渐完备应答域。根据科学问题扩张型情况，可以将该方法的逻辑结构形式表示为：因为W 中的背景知识BK 的不断加入，而不断使科学问题的应答域（即解空间）愈加完备，解空间不断完备的过程实则就是科学问题变为常规问题的过程，这里的解空间的完备含义不一定是解空间的收缩，而一定是使解空间边界愈加清晰，从而减低了科学问题的难度。对于某个科学问题P，设BKi和BKi+1是因新添加某个背景知识的前、后相继背景知识集，即BKi⊂BKi+1。一般而言，某个科学问题的背景信息已知的越少，解决问题的方向越容易跑偏，因而难度也越大；反之，背景信息知道的越详细、越具体，那么问题的解空间将会越清晰，因而科学问题也将逐渐转变为常规问题。所以，我们可以定义这种类型的科学问题的难度系数：若（BKi⊂BKi+1），则δ（LFS（P）BKi+1）≺δ（LFS（P）BKi）。

该公式的直观含义是用相同的逻辑函数作用于同一个科学问题时，背景知识越充分、越丰富、越具体，那么对该问题的解答就越容易，反之则越难。所以，在实际的科学问题研究过程中，要充分进行调查研究，毛泽东曾经说过：“没有调查就没有发言权”，应该可以从这个层面上理解。这里的调查实则就是不断挖掘与问题有关联的背景知识。

科学哲学已有的研究成果大多是集中对科学理论的产生和演化机制的研究。本文基于科学哲学的传统范式，初步涉足了科学哲学研究的另一个领域，即对科学问题的相关理论的哲学探讨。具体而言，本文进行了与科学问题的难度相关的一些哲学讨论：第一，科学问题的逻辑结构，并阐述产生科学问题的五种情形，即由于W 中的背景知识BK 的不完备所致、由于推理规则IR 的不完备所致、由于一个研究纲领的不同的辅助性假说所致、不同的理论范式PD 所致以及前几种情形的混合所致。第二，界定了科学问题的问题域及其空间的逻辑构型，即＜PD：SB+IR+LS＞。第三，定义了科学问题的应答域以及科学问题解空间动态变化的两种基本类型，即逐渐收缩型和逐渐扩展型。第四，基于科学问题解空间的变化类型定义了科学问题难度评价指标。第五，进一步得出科学问题难度消解的两个基本路径，其一是通过增加新的研究方法，从不同的研究视角锁定问题的解空间；其二是通过扩展背景知识以不断完备问题的解空间。

注释：

[1][2][3]H.A.西蒙：《人类的认知——思维的信息加工理论》，北京：科学出版社，1986 年，第59 页。

[4][9]林定夷：《问题与科学研究——问题学之探究》，广州：中山大学出版社，2006 年，第246、230 页。

[5][6][10]沈振东：《论科学问题的意义标准》，《科技进步与对策》2012 年第21 期。

[7]沈振东：《科学问题的逻辑系统构造》，《江苏第二师范学院》（社会科学版）2015 年第1 期。

[8]在早期的时候，人们都设想行星仅是以圆周运动环绕地球运动，并不足以完美解释行星多样化的运动。所以他们都想出是一个想象的小圆（而不是行星本身）在环绕地球作圆周运动，而行星就在这个小圆上运动。这个小圆就是本轮，而本轮环绕地球运动的轨道就是均轮。

[11]究竟哪些命题可以称为原子命题，哪些命题可以称为复合命题是相对于问题P 而言的。