基于光谱图像空间的F-SIFT 特征提取与匹配

丁国绅，乔延利，易维宁，李 俊，杜丽丽*

（1. 中国科学院安徽光学精密机械研究所通用光学定标与表征技术重点实验室，安徽合肥230031；2. 中国科学技术大学，安徽合肥230026；3. 西安科技大学安全科学与工程学院，陕西西安710054）

1 引 言

随着机器视觉的兴起，图像处理技术已经成为机器视觉不可缺少的组成部分。同时，图像中含有大量的信息，因此需要采用图像处理算法来提取图像的显著特征提高处理速度。图像特征是计算机视觉领域最重要的概念之一，从几何上可以将图像特征分为三大类：点特征、线特征和块特征［1-2］。基于不同的准则衍生出了诸多图像特征处理方法，并被广泛应用于目标检测、视频压缩、影像配准、三维模拟等领域［3-5］。由于传统的图像特征提取算法不能同时满足实时、高效、高精度的要求，学者们从不同的角度提出了许多优秀的特征处理算法。HOG（Histogram of Orientation gradient）［6］，PCA（Principle component analysis）［7］和Krawtchouk 矩阵法［8］是几种典型的区域块特征提取算法，由于块中包含更多的图像细节信息，因此在平行空间下能够取得良好的效果，但现实世界中的很多应用场景中的图像并不是通过单个相机拍摄得到，而是基于多角度、多维度汇总处理，这种对尺度和视角敏感的缺陷在很大程度上限制了此类方法的拓展空间。线特征能够规避区域特征存在的一些缺陷，但其对场景的要求也较为严格，所提取的目标线段应尽可能不被遮挡、不变形、不断裂，线段的空间完整性和尺度一致性是保证其最佳性能的前提［9］。点特征对于图像的旋转、拼接、尺度等维度上的变换适应性较前两种特征其鲁棒性更优，常见的点特征提取方法包括SURF（Speed Up Robust Feature）［10］，SIFT（Scale Invariant Feature Transform）［11］，ORB（Oriented Fast and Rotated Brief）［12］等。由于SIFT 算法是最早提出的基于尺度不变性的方法，其在图像旋转、视点和仿射变换条件下依旧能保持优良的稳定性，使得该算法被广泛应用于工业和实际生产中，也吸引了大批研究者的关注，从不同的方向对算法的性能进行了提升。

Yan 等在SIFT 方法中引入了2DPCA 算子重构低维度的描述子，将改进后的PCA 方法用于归一化特征描述子向量，大大压缩了算法的运行时间［13］。Rathgeb 等提出了基于SIFT 的虹膜识别方法，该方法增强了从近红外虹膜图像中获得的虹膜纹理归一化的效果，并将二值化技术纳入到整个系统中，对提取到的特征点做了二值化，形成了二值SIFT 描述子，相对传统SIFT 方法，系统最终的识别精度有了很大提高［14］。Xu等建立了基于图像局部信息的自适应分数阶微分的数学模型，建立最优阶数与图像局部信息的关系，并根据图像的特点自动计算出每个像素点的最优阶数，接着根据最优阶数和Riemann-Liouville分数阶定义构造了自适应分数阶微分动态掩模，提出了基于自适应分数阶微分的SIFT 算子［15］。

针对SIFT 算法提取的特征点数量较少的问题，在上一步的工作中我们开创性地提出了利用高光谱图像不同波段象元的DN 值差异重构图像金字塔的方法，使得提取到的特征点数量呈现了指数式增长［16］。但特征点数量的增加必然导致运行开销的增大，因此本文从两个方面对算法进行了优化。首先利用FAST 算法在像素级上快速筛选的特性，建立八邻域判断准则，将特征点数量降低到了初始值的1/10 以下，极大地降低了冗余特征点的数量；其次提出了双重位置迭代匹配方法，将描述符向量的扩展维进行排序，从可靠性程度最高的20 组匹配中迭代选择4 组构建双重三角平面，利用像素点的初始位置关系进行精确判断，实验结果表明没有误匹配出现。

2 传统SIFT 算法

SIFT 算法是1999 年由British Columbia 大学的David G. Lowe 教授提出并于2004 年加以完善的基于图像点特征的提取算法。该算法引入了尺度空间的概念，对光照、旋转、仿射以及尺度的变化都具有良好的稳定性，在学术界和工业界都产生了深远的影响。概括来说，SIFT 算法可以分为三个步骤。

2.1 关键点检测

给定输入目标图像I，对I分别进行一次升采样和O-1 次降采样，每次采样都以当前图像为基准做高斯变换。其中，高斯核函数G的表达式为：

其中：xt，yt分别是图像I的第t个像素点的像素值，σ是采样尺度，每次采样之后的图像I(xt，yt，σt)=G(xt，yt，σt)*I(xt，yt)。在构建完图像的尺度空间后，利用高斯差分的性质建立图像差分空间，即用图像金字塔中的每一组图像中的第k层减去上一层即可得到。最后比较差分空间每组图像中除去首尾两层剩下的每层图像的各像素点与其相邻的26 个像素点的差异，若该点在此27 个像素点中是极大值或极小值，则认为该点是候选关键点。

2.2 关键点定位

通过差分空间检测可以得到一系列离散的极值点，但实际上关键点可能存在于两个极值点之间，因此这就需要通过插值的方式得到真正的关键点。根据泰勒函数的性质，对尺度空间函数进行泰勒拟合，得到亚象元级别的DOG 函数，其表达式为：

2.3 描述符生成

由于拍摄的角度不同，同一目标在不同图像中会存在不同程度的旋转以及仿射变换，因此在确定关键点的位置之后还需能唯一表征此描述符的方向信息。SIFT 算法依据当前关键点的4×4 邻域内的像素信息统计其像素梯度分布，其梯度值和对应的方向如下：

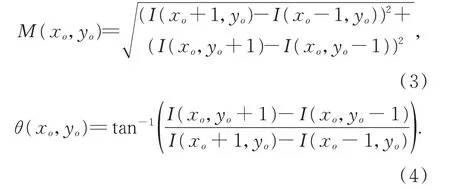
对于邻域内的每个子区域，将其梯度分布平均划分为8 个方向，统计每个方向区间内的梯度值之和，最终形成128 维的梯度向量。取梯度值最高的方向为描述符的主方向，最后对所有梯度向量进行归一化处理，形成SIFT 特征描述符。

3 基于光谱图像空间的F-SIFT 特征提取与匹配

在本节中，优化并进一步完善了基于光谱图像空间的SIFT 算法［16］，在特征点的数量上取得突破的同时降低冗余特征点的占比，极大地提高了特征点的有效利用率，并且采用独特的双重迭代优化的方法来剔除误匹配，整个方法的流程概括如下。

3.1 构建光谱图像空间

传统SIFT 算法的尺度空间是由一张输入图像经过升采样和降采样并且对于同一分辨率的图像采用不同模糊系数进行高斯模糊得到不同模糊程度的子图像集合。这种做法能够解决两张图像因为尺度不同而难以配准的问题，同时对图像的仿射变换具有一定的鲁棒性，因此在后续诸多改进的SIFT 方法中都保留了这一做法［13-14］。虽然SIFT 算法在不同尺度的图像上稳定性较好，但其尺度空间仅由一幅图像经系列变换得到，所带有的有效图像特征信息十分有限，因而提取到的图像特征点数量较少。高光谱图像在不同波段上的图像具有良好的相似性，目标在不同波段图像上的位置相同而DN（Digital Number）值不同，也即传统意义上的灰度值不同，但其所表征的同一目标的DN 值趋势相同。利用这个特性，用可见光范围内的高光谱图像作为尺度空间的基准图像，并对其进行直接降采样得到图像的尺度空间，示意图如图1 所示。

图1 高光谱图像尺度空间Fig. 1 Hyperspectral image scale space

3.2 FAST 八邻域准则

在重构了图像的尺度空间后，可提取到的图像特征点的数量较传统SIFT 算法提升了几十至几百倍，克服了原SIFT 算法提取的特征点数量少的缺陷。但通过实验验证发现，虽然有效特征点的数量有了很大提升，但相较于特征点总数的指数级规模的增长，冗余特征点的数量明显具有相当的规模，因而如何降低冗余特征点的占比是本文的研究内容之一。

FAST 算法是特征点检测中最直观地用原始图像像素点与其邻域内像素点的差异值来判断是否为特征点的方法之一。虽然该方法检测到的特征点不一定是最优特征点，但其快速选择的特性在本文中被融合到了差分金字塔的判定中。原FAST 算法是在较大的邻域空间上对目标位置的像素值进行比较，虽然大部分的情况下像素值的变化趋势相似，但在像素值有明显突变的时候邻域范围较小更能较好地表征目标像素点的周围像素变化。因此本文采用了3+2+3 的目标像素八邻域的方式，在构造差分金字塔中的每一层图像时对该图像上的像素做预筛选，若邻域内有M个点的像素值大于阈值T则保留该点的像素值，否则将该点的像素值置为-1。在特征点的判断阶段则首先判断该点的像素值是否为-1，若是则直接进入下一个特征点的判断阶段。经实验验证，加入FAST 八邻域准则之后，F-SIFT 算法所提取到的特征点数量降到了文献［16］中算法的1/10 以下，且最终成功匹配的特征点数量不受大的影响。

3.3 双重位置迭代匹配

在完成特征点的提取之后要对两幅图像之间的特征点进行匹配，常见的方法是采用最近邻与次近邻的比值来选取最优匹配。这种方法是基于像素梯度值的分布来衡量特征点的相似程度的，图像中往往会存在一个或多个相似的特征点，这就容易造成误匹配现象，而且该方法对于比值阈值的确定异常敏感。传统SIFT 算法在进行特征点匹配时常将比值设定为0.8，涉及到具体图像时还会有小范围的波动。这是因为当比值增大时匹配到的特征点数量会随之增加，有效匹配和误匹配数量也会增大；当比值减小时匹配到的特征点数量会随之降低，虽然误匹率降低但成功匹配的数量也明显衰减。

针对这种情况，本文提出了双重位置迭代匹配方法，将整个特征点的匹配过程分为两步。首先采用最近邻与次近邻之比对特征点进行一次粗匹配，不过在此阶段的比值设定较大，目的是为了尽可能多地包含有效匹配对，经实验验证此阶段的理想比值H设定为1.1。接着进行精细匹配操作，在粗匹配阶段依据最近邻与次近邻的相似性对特征点的描述符向量进行了一维扩展，虽然这一阶段的匹配中包含了大量的误匹配，但精细匹配的作用就是剔除这些误匹配。将匹配到的特征点对按照相似性程度进行排序，然后从相似性程度最高的20 组匹配对中随机选择4 组构建源-目标图像双三角平面。在之前的工作中选取的是相似性程度最高的3 组匹配对来构建三角平面，但经过后来的实验发现这种情况下依旧可能出现误匹配的现象，因为只有在没有噪声的理想情况下才能通过三个点来构建一个完整的平面。为了排除噪声的干扰，本文采用了4 组匹配对来构建双三角平面，即用排列组合的方式随机从4 组中选取两个三维组合用来构建两个三角平面，最后根据所有匹配对的特征点在双三角平面中的位置关系进行是否为正确匹配对的判定。另一方面，没有采用相似性程度最高的4 组匹配对是因为图像上会存在相似的特征点，将其作为基准点构建三角平面可能会包含更多的正确匹配信息，因而在一定的区间上取出4 组匹配对会更有益。在兼顾算法效率的基础上将此区间设定为1～20。由于图像是用二维来映射三维空间位置关系的，因此用二维平面上的位置关系来阐述双三角平面的构建原理。

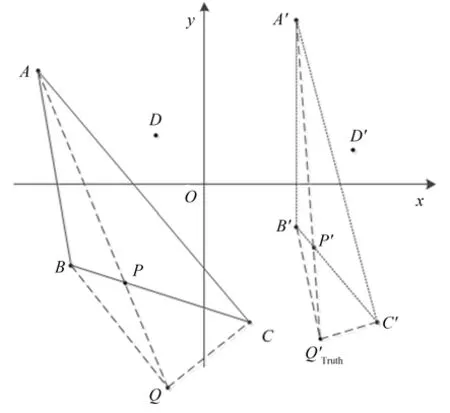
图2 双重位置迭代匹配Fig. 2 Double position iterative matching

如图2 所示，特征点集合(A，B，C，D)与(A′，B′，C′，D′)分别是源-目标图像中选取的4 对基准特征点对，对应关系分别是：A↔A′，B↔B′，C↔C′，D↔D′，↔表示匹配关系。Q点是源图像中的某个特征点，假设Q′是Q点在目标图像中匹配到的特征点。 因为(A，B，C，D) 与(A′，B′，C′，D′) 是基准特征点对，故三角平面O(A′，B′，C′)可由O(A，B，C)经系列平面变换操作生成。直线L(B，C)中存在如下等式：

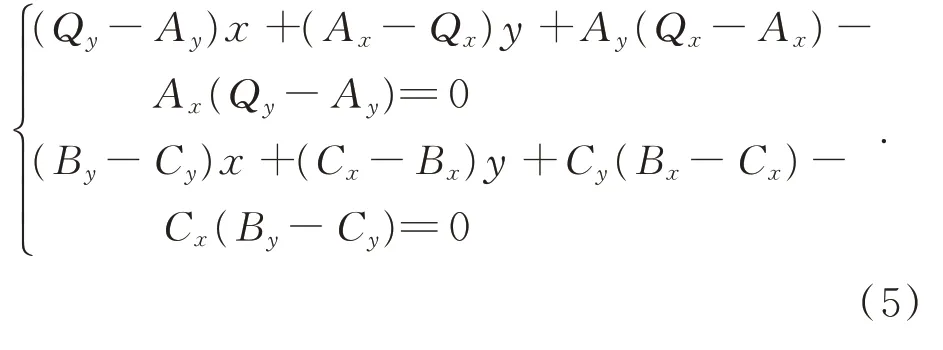
设R1=Qy-Ay，S1=Ax-Qx，T1=Ay(Qx-Ax)-Ax(Qy-Ay)，R2=By-Cy，S2=Cx-Bx，T2=Cy(Bx-Cx)-Cx(By-Cy)，可得点P坐标：

一般来说，天线的中心频率越高，分辨率越高，探测深度越浅；反之天线中心频率越低，分辨率越低，探测深度越深。不同中心频率天线的穿透深度如表1。

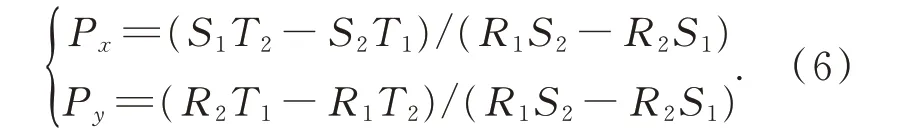
设M=|BP|/|BC|，N=|AP|/|AQ|，有如下等式成立：

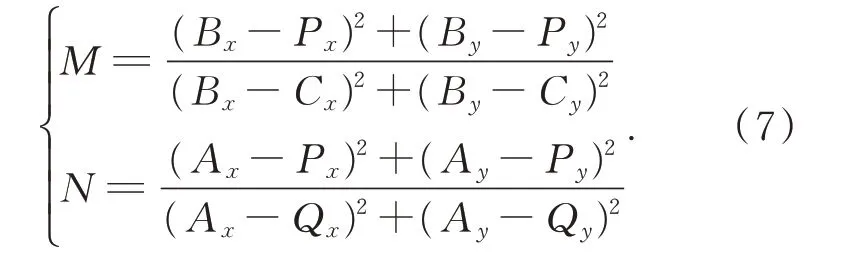
因为平面O(A，B，C)与O(A′，B′，C′)中各点的相对位置是相同的，因而存在如下关系：

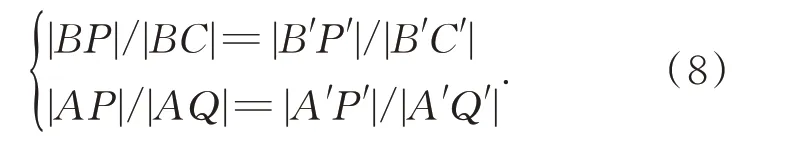
求得P′坐标：

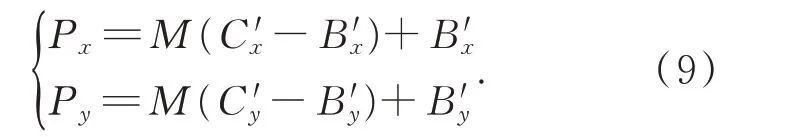
进而可得到理想情况下的Q′点的坐标，接着计算Q点实际匹配到的点Q′Truth与Q′ 的位置误差δ1：

同理可得到Q′Truth与Q′在平面O(B，C，D)与O(B′，C′，D′)中的误差δ2，若δ1与δ2均在允许误差范围内则认为Q与Q′是一对正确匹配对，否则剔除这对匹配。

4 实验结果与分析

因为基于高光谱图像的SIFT 算法是由我们首次提出的，并未出现此方面的公用数据集，结合实验需求，本文所用数据集都是基于IS210-0.4-1.0-L 型号的高光谱成像相机拍摄的，数据集链接为：https：//pan.baidu.com/s/1qYEymTvj_wjVZEoj6wLfvQ。实验的硬件环境为Windows10 （64bit） ，Intel （R） Core （TM） i7-9700CPU @ 3.00 GHz 处理器，编程环境为MatlabR2020a。本次实验分为两组，在可见光波段范围内选取的波段间隔为10～50，精细匹配阶段的迭代次数设置为1 000，验证F-SIFT 算法对于简单和复杂目标情况下的基于不同波段间隔的算法性能。

图3 和图4 分别是传统SIFT 算法与F-SIFT算法在单一目标和复杂目标场景下的图像特征点匹配结果，图像波段间隔为25，其中图3（a）～3（b）图是传统SIFT 算法在最近邻与次近邻的比值为0.7 和1.1 时得到的，图3（c），3（d）图时FSIFT 算法在最近邻与次近邻的比值为0.7 和1.1 时得到的。由图中可以看出，对于传统SIFT，在最近邻与次近邻的比值设定较小时算法提取到的特征点数量相对较少，误匹率较低；增大比值能够较大提升特征点提取能力，但误匹率也随之增加，这种结果往往是不能忍受的。而对于F-SIFT 算法，虽然在最近邻与次近邻的比值较小时算法在某些场景下提取到的特征点数量有限，但能保证剔除所有误匹配，而且随着比值的增加这种零误匹率的优势更加明显，在比值为1.1 时算法能同时兼顾特征点数量与正确匹配率两大优势，具有良好的应用潜力。

图3 单一目标的特征点匹配结果Fig. 3 Feature point matching results of single target

图4 复杂目标的特征点匹配结果Fig. 4 Feature point matching results of complex target

表1 和表2 分别记录了在单一和复杂目标场景下传统SIFT 算法与F-SIFT 算法在不同最近邻与次近邻比值的情况下特征点匹配对数。其中SIFT-O 表示传统SIFT 算法只在最近邻与次近邻比值规则下得到的匹配对数目（包含不同程度的误匹配数目），SIFT-F 表示在双重位置迭代匹配准则下传统SIFT 算法得到的匹配对数目（不包含误匹配）。由表中数据可以看出F-SIFT算法较传统SIFT 算法其有效特征点匹配对数提升了几十至上百倍，而且由于在匹配阶段采用的双重位置迭代匹配准则，这些匹配对中均没有误匹配。而且随着最近邻与次近邻的比值不断增大，F-SIFT 算法的性能优势更为突出。另外，从波段间隔的变化上可以发现，在用高光谱图像重构尺度空间时，并不是波段间隔越大或越小算法的性能越好，这从图像层面上也很好理解。在波段间隔过小时，相邻波段的图像之间的差异很小，提取到的特征点信息就更接近，也即多样化信息就越少，因而能提取到的特征点数量就越少；在波段间隔过大时，不同波段之间的图像差异太大会对差分金字塔的特征点的确定造成负面的影响，因而也会导致提取到的特征点数量降低。

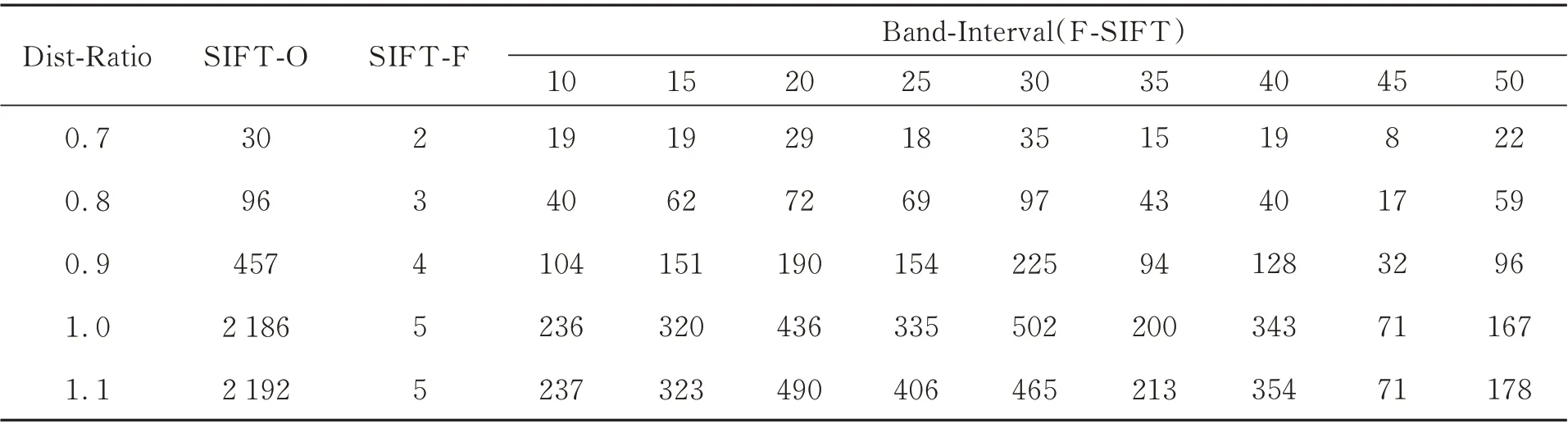
表1 各波段下单一目标匹配数量Tab. 1 Matching number of single target in each band

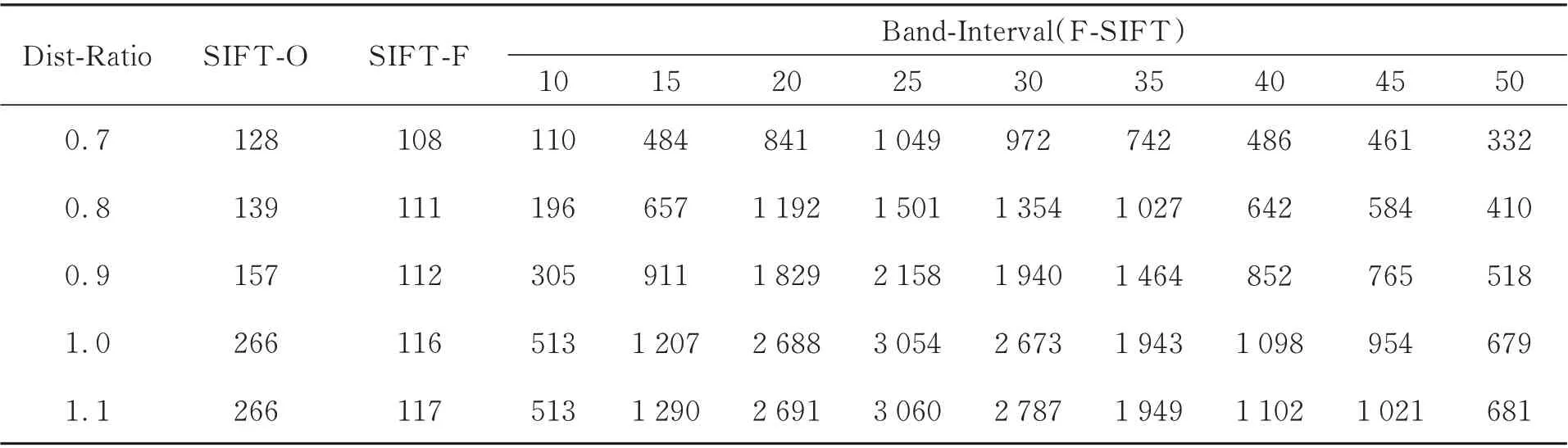
表2 各波段下复杂目标匹配数量Tab. 2 Matching number of complex target in each band

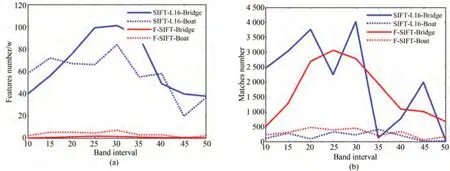
图5 F-SIFT 算法与文献［16］中算法在不同波段下的特征点与匹配对数量曲线Fig. 5 Number curve of feature points and matching pairs of f-sift algorithm and the algorithm in reference［16］under different wave bands

图5（b）表示F-SIFT 算法与文献［16］中算法在不同波段下得到的最终正确匹配对数，由于文献［16］中可能含有误匹配，因而采用了相似性程度最高的4 组匹配对用来构建双三角平面。由此也可以看出相似性程度越高并不一定就意味着是最佳的选择，经实验反复验证，从前20 对相似性程度高的匹配对中随机选择基准特征点对能扩大算法的性能优势。

5 结 论

图像处理是机器视觉领域最基础的研究工作之一，特征点提取与匹配在图像处理中有着举足轻重的位置，良好的特征点获取与检校方法对于后期的工作具有重要的意义。因此本文从SIFT 算法出发，对先前的工作进行了优化和总结，提出了一种基于光谱图像空间的F-SIFT 特征提取与匹配方法。该方法从图像的尺度空间的构建、冗余特征点的删减、误匹配的剔除三个方面进行了改良，构造了一种新颖有效的图像特征点处理方法。接下来准备从高光谱图像本身出发，研究不同分辨率下的高光谱图像构造出的尺度空间对算法最终结果的影响，以及将本文方法引入图像的三维重构中，拓展算法的应用领域。