基于测量基优化的低采样率单像素成像

赵梓栋，杨照华*，李高亮

（1. 北京航空航天大学仪器科学与光电工程学院，北京100191；2. 北京华航无线电测量研究所，北京100010）

1 引 言

二维图像是如今应用最为广泛的光电信息之一。传统成像基于阵列探测器的透镜成像原理。作为传统成像方式的一种替代，单像素成像在时序上记录每个测量基掩膜基的光强信息，在阵列探测器昂贵的非可见波段和极弱光探测下相较传统成像方式优势明显。然而，单像素成像需要投射大量的散斑并记录光强信息，这无疑会造成存储空间及时间的浪费，从而限制单像素成像的实际应用。在已有的研究中，成像效率的提升主要体现在优化重构方法和优化采样散斑上。

在优化重构算法方面，传统的计算关联成像使用关联算法来重构物体图像，之后在此基础上提出了差分鬼成像和归一鬼成像算法。随着压缩感知理论的提出，研究人员发现压缩感知的线性测量模型与计算关联成像的测量过程相同，并在此基础上提出了单像素相机［1］。压缩感知利用自然物体在某些测量基下的稀疏特性，以计算资源的代价换取在极低采样率下的成像，目前已经在核磁共振、天文观测及显微成像中有着极为重要的应用。然而，对于中等分辨率的图像，传统的压缩感知在采样率低于30%下很难获取高质量的重构图片。因此，人们将压缩感知和深度学习相结合，但这种方法明显的缺点就是需要大量的训练时间和数据集，因此很难实现应用。

在优化采样散斑方面，传统的计算关联成像使用的是随机散斑，这种散斑的非正交性导致对一张分辨率为N的物体成像时投射的掩膜矩阵数量需要远高于N。为提升成像效率，主流算法使用的掩膜矩阵为正交测量基，如傅里叶测量矩阵或哈达玛测量矩阵。其中，哈达玛矩阵构造简单，易于二值化，是最常使用的掩膜测量矩阵。在欠采样条件下，测量基的选择对成像的结果有着显著的影响。因此，国内外先后提出了针对哈达玛矩阵的俄罗斯套娃排序（Russian Doll，RD）［2］、切蛋糕排序（Cake Cutting，CC）［3］、进化压缩感知（Evolutionary Compressed Sensing，ECS）［4］和小波系数排序等排序方法［5］。采用这些方法排序的哈达玛矩阵相对于未排序的哈达玛矩阵，作为调制的掩膜矩阵在提升成像效率和减少测量次数上的优势明显。但这些排序方法都是固定准则，在某些条件下成像效果可能较差。本文提出一种基于训练集数据统计的哈达玛散斑排序方法，在计算重构时使用快速沃尔什哈达玛变换［6］来代替传统运算中矩阵的乘法运算，不仅可以加速训练和重构过程，在分辨率较大时还可以大幅减少存储资源。

2 理论和方法

2.1 单像素成像理论

单像素成像光路如图1 所示，其中数字微镜阵列（Digital Micro-mirror Device，DMD）为核心器件。激光发出的光经过成像透镜到DMD 上后打到成像物体上，反射或者投射的光被单光子探测器接收。DMD 上有数百万个可控制±12°偏转的微镜，每个微镜的偏转方向由加载到DMD上的调制矩阵决定，如矩阵元“1”对应+12°方向偏转，矩阵元“-1”对应-12°方向偏转。在实际成像过程中，调制矩阵序列不断刷新，对应着光强信号不断变化，将光信号转化成的数字信号并和加载在DMD 上的调制矩阵序列经过相关算法计算，即可恢复出重构图像的信息。

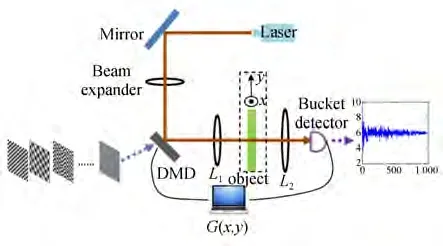
图1 单像素成像光路Fig.1 Optical path of single pixel imaging

在实际成像过程中，单像素成像常常受制于实时性的要求，因此压缩感知被引入到单像素成像的重构算法当中。单像素成像的数学模型如下：

式中：x为1×M维向量，表示待测物体的二维图像，而加载到DMD 中调制矩阵序列中的每个调制矩阵可以变为1×N维的向量；M个调制矩阵序列构成了一个已知的M×N的测量矩阵A；观测值对应M个调制矩阵为1×N维的向量y；e代表成像过程中的随机噪声。从公式（1）中可以看出，每一个桶探测器信号理论上是每个掩膜和目标图像做内积得到的。图像重构过程可以通过凸优化的相关算法来求解。

在评价重构图像的质量时，本文采用两项评价指标：均方根误差（Root Mean Squared Error，RMSE）和峰值信噪比（Peak Signal to Noise Ratio，PSNR）。PSNR 是一种全参考的图像质量评价标准，是最大信号功率和噪声功率的比值，其计算公式为：

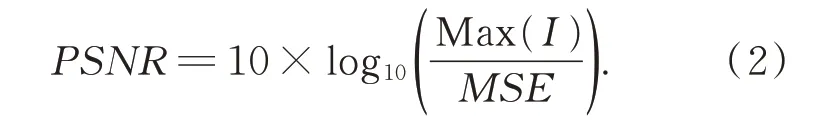
RMSE 计算的是被污染重构图像和原图的均方根误差，假设I是原图，K是重构图片。RMSE 的计算公式如下：

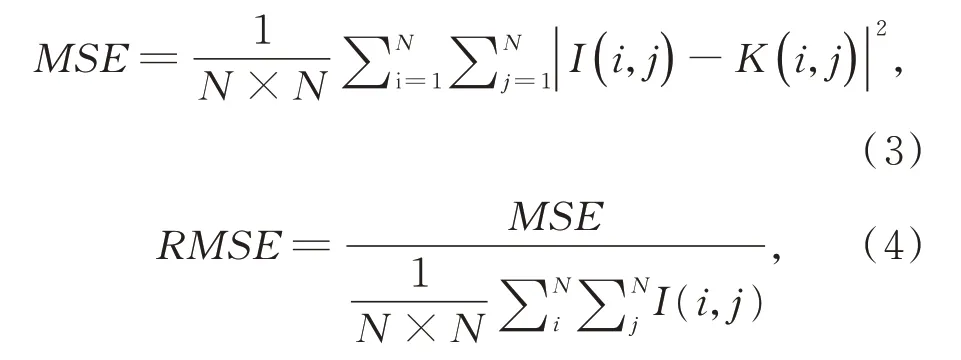
其中N是图像的像素数。在衡量重构质量时，PSNR 越大，RMSE 越小，重构图片的质量越好。

单像素成像中使用的重构算法主要有两种［7-12］：第一种是Li 等于2010 年提出的基于增广拉格朗日和交替方向的TV 最小化方案（TV minimization scheme based on Augmented Lagrangian and alternating direction algorithms，TVAL3）；第二种是Czajkowski 等在2018 年提出的傅里叶正则化方案（Fourier Domain Regularization，FDRI）。两种算法对lena 图片的重构结果比较如表1 所示。

从表1 中可以看出，FDRI 算法的成像效果在采样率低于15%的情况下和TVAL3 算法的重构效果相当。而由于FDRI 算法中并没有迭代运算，其重构时间小于TVAL3 算法，因此本文采用FDRI 算法作为重构算法。

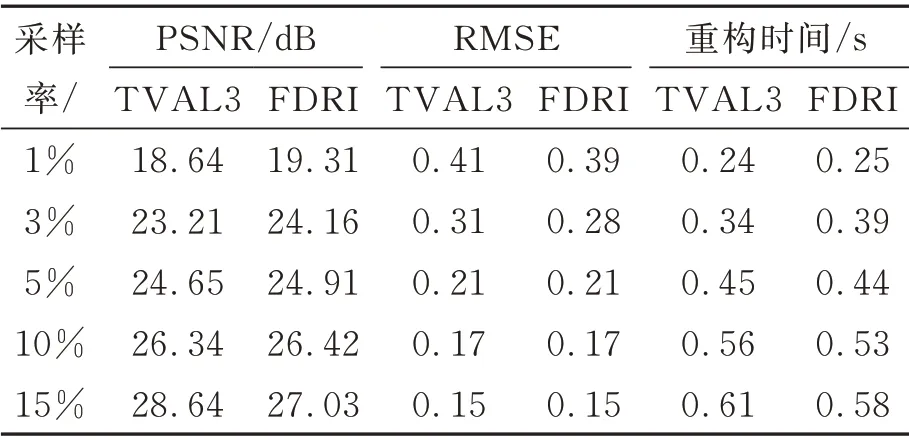
表1 TVAL3 和FDRI 算法重构效果的比较Tab.1 Comparison of reconstruction results of TVAL3 and FDRI

2.2 数据驱动的矩阵排序方案

为减少单像素成像过程中所需投射的散斑数目和重构时间，在压缩感知重构算法下如何利用图像本身的稀疏性来构造出一组测量基，使成像物体的重建效果和效率在相同采样率下达到最优是关键。在单像素成像中，最常使用的测量基为Hadamard 矩阵测量基，其各个元素二值和完备正交测量基的属性使它成为研究的重点。哈达玛测量基的排序方案主要有切蛋糕排序、俄罗斯套娃排序和小波系数排序等，其核心在于分析特定哈达玛矩阵测量基的几何拓扑结构，然后人工给出确定的排序准则。这些准则固然能反应哈达玛矩阵的一些性质，但人工确定的准则存在一定的误差，且在排序指标相同的情况下无法进行排序。因此，本文提出一种数据驱动的哈达玛测量基排序方案，用测量基中各个矩阵对整个数据集的采样效果进行评价。

图2 不同排序在不同采样率下的成像效果Fig.2 Reconstructed images in different orders at different sampling rates

在单像素成像的欠采样成像过程中，选择不同部分的桶探测器值参与最后的重构运算对成像效果的影响很大。如图2 所示，在低采样率下自然序和随机序下图像的重构效果极差，而进化压缩感知方法将桶探测器值的绝对值从大到小排序，使用前部分桶探测器值进行重构，其效果明显优于另外两种方法。由此可知Hadmard 矩阵排序的任务是：找到一个和Hadamard 矩阵自然序（或者Walsh 序）对应的索引，按此索引排序的Hadamard 基在实际问题中对一张未知物体采样后的结果可以产生相对较大的桶探测器值，生成质量相对较高的重构图像。由于事先没有图像信息，无法知道哪些散斑对重构最为重要，因此最基本的想法是对物体全采样后的桶探测器的绝对值进行降序排序，排序后再使用前m张散斑参与重构。这种方法被称为进化压缩感知，这种Hadamard 基的顺序被称为power 序。该方法虽然可以利用较少的测量结果取得质量较高的重构图像，但实质上仍然是全采样，只是减少了重构的运算量，并没有减少测量时间和重构时间。

在此排序方法的基础上，本文提出了基于数据集学习的Hadamard 矩阵的排序方法。其基本步骤如下：在训练之前确定输入图片采样率r和图片大小p×p。训练过程中使用CIFAR-10 数据集包含的10 类，10 000 张32×32 分辨率的图片。训练的具体步骤如下：对训练集合中的每张图片转成p×p像素的图片。用自然序哈达玛基对图片进行全采样，得到该图片的桶探测器值序列bi，对bi每个元素的绝对值进行降序排序，排序后可得到降序的，同时可以获得相对于各位置元素改变的序列Ii，该序列是{1，2，…，p2}序列的重新排列。对数据集的n张图片进行上述操作得到序列Ii，Ii的含义是对第i张图片散斑序列投射的先后顺序。将每个Ii作为新矩阵Iset的每一行，构成索引矩阵整体流程如图3所示。

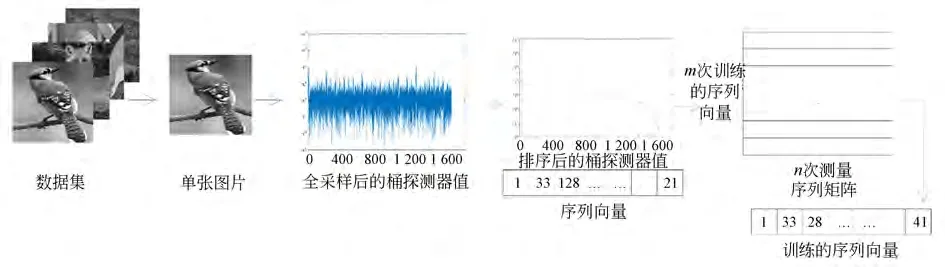
图3 数据驱动获取哈达玛矩阵部分测量序列的流程Fig.3 Pipeline of training order of Hadamard matrix in data driven

3 结果与讨论

为验证本文提出的排序方法的有效性，本文进行了仿真实验和实物实验。在仿真实验中，选用20 张测试图片进行测试。对测试集里每张图片进行1%～15%极低采样率下的成像，图像尺寸为128×128 像素。实验中，比较的排序规则有4 种：（1）哈达玛矩阵自然序（natural），即按哈达玛矩阵原始构造公式下的顺序；（2）切蛋糕排序（CC），按哈达玛矩阵各测量矩阵连通域个数从小到大进行排序的结果；（3）俄罗斯套娃排序（RD），将整个哈达玛测量基分为4 部分，再将第一部分进行递归式的切分，每一部分再按一定规则进行排序；（4）数据驱动训练排序，即本文提出的排序方案。

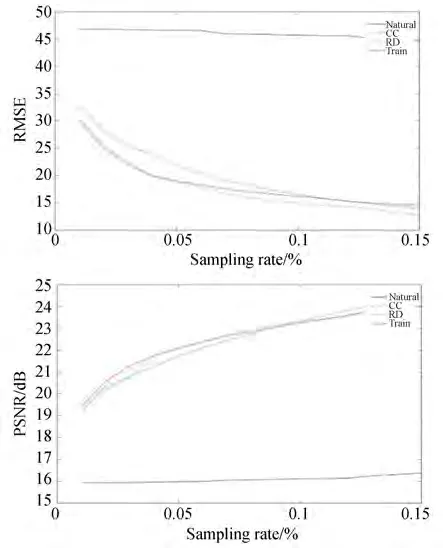
图4 不同顺序及采样率下重构图片的PSNR 和RMSEFig.4 RSNR and RMSE of different orders and sampling rates

仿真结果如图4 所示，不进行排序的自然序下的哈达玛矩阵的成像效果最差，使用压缩感知相关算法仍无法实现极低采样率下的单像素成像；而在1%～6%更低的采样率下数据训练的效果会明显优于另两种人工确定准则的排序方法，在5%～15%的采样率下和其他方法的重构结果相当。而考虑到训练的图片集合和重构图片像素并不相同（训练中将训练集图片放大到测试图片的尺寸），且训练图片和测试集图片完全不相关，因此该结果仍有提升空间，证明数据驱动的哈达玛矩阵排序方法在原理上优于人工确定准则的哈达玛矩阵排序方法。

选用分辨率板作为成像物体，实验成像效果如图5 所示。在仿真实验的基础上还加了几种排序方法：（1）哈达玛随机序（random）：将哈达玛矩阵每一行随机排列；（2）进化压缩感知（ECS）：进行全采样，将桶探测器值从大到小进行排序，再选取其部分参与重构。

从重构结果中可以看出，ECS 的成像效果最优，这是由于它采用了全采样和排序的结果；而自然序和随机序完全无法满足低采样率下的成像要求，本文提出的数据驱动排序方法和CC 排序和RD 排序的成像效果相差无几，在成像细节上效果更优。

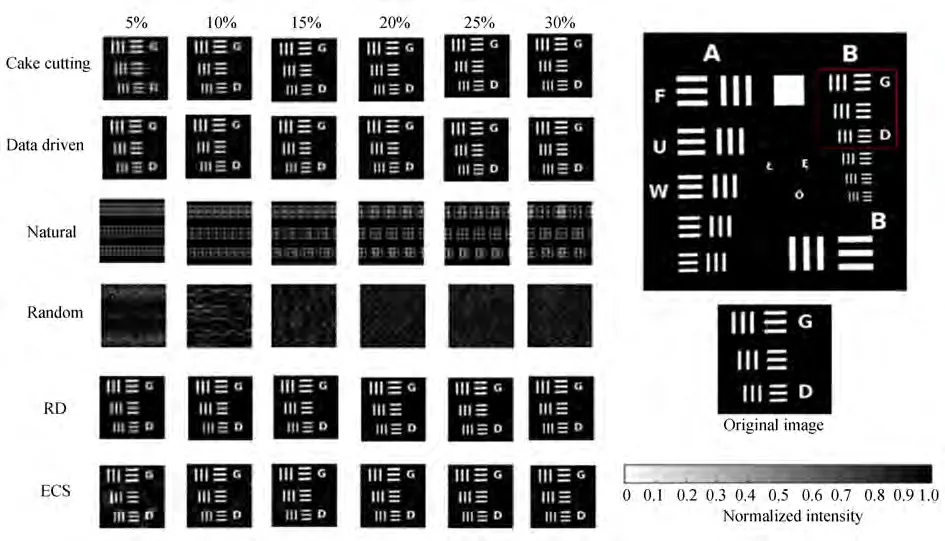
图5 分辨率板在不同顺序及采样率下的成像效果Fig.5 Reconstructed images of USAF resolution test chart with different orders and sampling rates

4 结 论

为解决实时成像中极低采样率下的单像素成像问题，本文提出了基于数据集训练的Hadmard 矩阵排序方法，并在理论、数值仿真以及实际成像实验上进行了研究及验证。结果表明：在1%～5%的采样率条件下，数据驱动的哈达玛矩阵排序方法相较目前常用的RD 排序和CC 排序成像效果更优。本文在理论上说明了利用数据学习训练的方法可以在非全采样条件下对实际成像物体产生较大桶探测器值序列，并提出了一种研究单像素成像中最优测量基选取问题的新思路，在非人工确定排序的情况下确定欠采样条件下的散斑序列，具有实际应用价值。