基于一阶自卷积Kaiser窗的分频段谐波检测DFT算法
2021-07-02谢业强王钢曾德辉
谢业强,王钢,曾德辉
(1.华南理工大学 电力学院,广东 广州 510641;2.广州嘉缘电力科技有限公司,广东 广州 510610)
电力谐波检测是电网谐波得到有效治理的前提。电力电子化电力系统的谐波特性已发生变化,谐波带宽大幅拓宽以及噪声干扰加剧给电力谐波研究提出了新的挑战。目前许多先进的算法被用于谐波检测,比如小波变换[1-3]、谱估计[4]、希尔伯特黄变换[5-6]以及神经网络[7]。小波变换是时-频算法,具有良好的时域特性,但当谐波成分过多时会造成严重的混叠现象,不适合弱谐波分量较多的宽频信号检测;谱估计算法理论上具有无限的分辨率,但该算法受噪声干扰严重,计算量大且易出现虚假分量;希尔伯特黄变换具有良好的暂态特性,但存在严重的模态混叠现象,同样不适合于宽频信号检测;神经网络具有很强的自适应性,但检测精度十分依赖于初始样本。因此,综合考虑带宽信号所要求的处理效率和检测精度,上述方法都不能满足电力电子化条件下的电力谐波检测要求。离散傅里叶变换(discrete Fourier transformation,DFT)[8-10]易于写入嵌入式系统且具有计算量小、效率高、操作简单等优点,然而DFT存在固有的性能缺陷,如频谱泄漏和栅栏效应。
目前,针对DFT谐波检测算法固有性能缺陷的研究,已取得一定成果。为了降低频谱能量泄漏,最常见的策略是采用窗函数对信号进行加权,(比如三角窗[11]、平顶窗[12]、汉宁窗[13-14]、Blackman窗[15]、Nuttall窗[16]等经典窗函数),但是经典窗函数的主瓣宽度是固定的,无法同时保证旁瓣峰值低和快速的旁瓣衰减特性,性能有待提高。与经典窗相比,Kaiser窗[17-18]能够通过改变调节因子使主瓣能量与旁瓣能量之比近乎最大,且能够自主选择主瓣宽度和旁瓣高度间的比重[19],因此信号加权更灵活。另外,通过对窗函数进行时域自乘运算[20]或卷积运算[21]可进一步提高窗函数抑制频谱泄漏性能,但时域自乘运算会导致窗函数的主瓣宽度变宽[22],降低频率分辨率而不利于宽频信号检测。为了减少DFT栅栏效应引起的理论误差,可借助校正措施给予修正,如谱线插值算法[23]。根据紧邻频域峰值点加权谱线的数量,可分为双谱线、三谱线、四谱线插值算法[24]等,加权谱线数量越多校正效果越明显,但加权谱线的增多也会导致计算量增加[25]。当前,校正算法须在频率估计值已知的情况下,才可求解相位估计值,这会将频率估计误差累计到相位测量中,造成测相精度受到影响,在噪声环境下更加显著。文献[26]提出一种名为全相位快速傅里叶变换算法(all phase fast Fourier transformation,APFFT),其原理可简单概括为在进行DFT算法前对原始数据进行全相位数据预处理,使得APFFT具有相位不变的优良特性,理论上可以借助精确的相位差值去校正频率和幅值;但全相位数据预处理会导致栅栏效应加剧,使得频率与幅值测量存在较大的理论误差,尤其是弱谐波分量。
对此,为综合提高宽频谐波信号检测的精度、稳定性和抗噪性能,在研究窗函数自卷积运算、谱线插值算法以及全相位数据预处理算法优缺点的基础上,实现优势互补,提出基于一阶自卷积Kaiser窗的谐波检测DFT算法。为降低宽频信号的检测时间,对宽频信号进行分频段处理,提出分频段的谐波检测DFT算法,有效地降低高频段的检测时间,在保证检测精度下提高计算速度。所提算法通过频段划分能有效解决宽频信号中高频段谐波检测计算时间冗余问题,以及通过自卷积运算实现全相位数据预处理算法和谱线插值算法的优势互补,综合增强宽频谐波检测算法性能。最后,构建包含50倍基频多正弦复杂信号模型,并引入基波频率波动和白噪声干扰测试验证所提算法对宽频谐波检测的可行性。
1 基于一阶自卷积Kaiser窗的改进算法
加窗DFT算法经过谱线插值校正以后具有良好的频率和幅值检测精度,但存在频率估计误差蔓延问题,进而影响到相位检测的精度。通过全相位数据预处理的DFT算法具有相位不变特性,能够解决谱线插值DFT算法的频率误差蔓延问题;然而,原始数据经过全相位数据预处理算法后,数据长度变长即由原来的N个点变成2N-1个点,不能与DFT算法直接融合实现互补,而通过对窗函数进行自卷积运算能解决上述问题。故须研究Kaiser窗函数的频谱泄漏抑制性能以及自卷积运算对Kaiser窗的影响。
1.1 Kaiser窗
Kaiser窗的时域表达式[27]
(1)
式中:n=0,1,…,N-1为采样序列;N为窗函数长度;I0(β)为零阶贝塞尔函数,其中β为调节因子,函数表达式为
(2)
长度为N的Kaiser窗频域表达式
(3)
式中ω=2πk/N,k为谱线位置。
对Kaiser窗进行一阶自卷积运算并归一化得2N-1点的时域归一化卷积窗
(4)
式中w(n)*w(n)为一阶自卷积运算。
归一化卷积窗的频域表达式
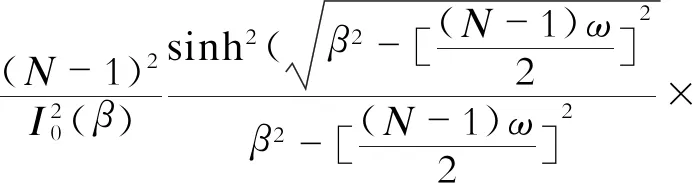
(5)
式中上标*表示自卷积后的窗函数。
图1给出长度N=25的Kaiser窗的归一化对数频谱,其中图1(a)—(d)分别为β=0、4、8、11时,Kaiser窗的归一化对数频谱,其中“dB/oct”表示每2倍频的分贝变化量。图2展示一阶自卷积Kaiser窗与Kaiser窗的归一化对数频谱对比。
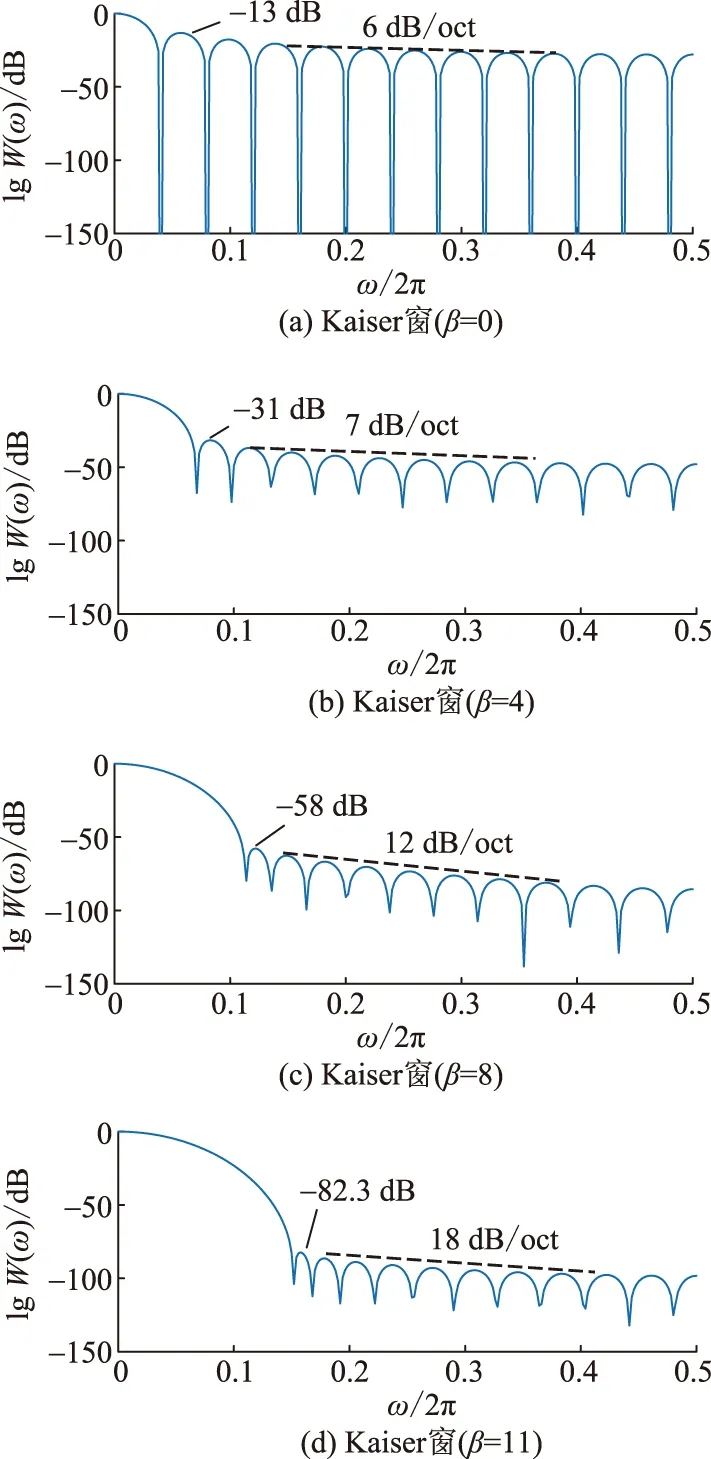
图1 Kaiser窗的归一化对数频谱Fig.1 Normalized logarithmic spectrum of Kaiser window
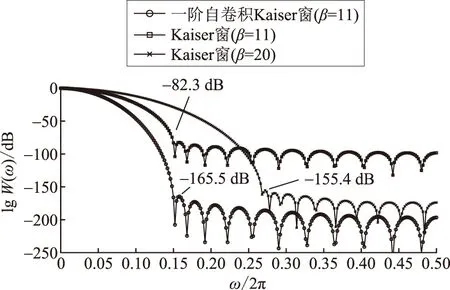
图2 一阶自卷积Kaiser窗与Kaiser窗的频谱对比Fig.2 Comparisons of spectrum between 1st-order Kaiser self-convolution window and Kaiser window
选择窗函数时需要考虑被检测信号的特性。由于电力电子化电力系统的谐波带宽大幅拓宽以及噪声干扰严重,这不仅要求窗函数具有良好的旁瓣特性,而且还要求具有窄的主瓣宽度。但是对窗函数而言,主瓣宽度和旁瓣性能是固有的矛盾体,即频率分辨率和频谱泄漏抑制能力不能同时兼得。由图1(a)—(d)可知,当Kaiser窗随着β值的提升,旁瓣峰值与主瓣峰值差值越大且渐进衰减速度越快,具有更高的抑制频谱泄漏能力;然而,随着β值的增加,Kaiser窗函数的主瓣宽度越宽,这将导致频率分辨率的减低,不利于宽频谐波的检测。由图2可知,Kaiser窗在进行一阶自卷积运算时,能够在不改变主瓣宽度的情况下,进一步降低旁瓣峰值和加快衰减速度,从而提高抑制频谱泄漏能力。此外,一阶自卷积Kaiser窗(β=11)的旁瓣性能可以媲美调节因子β=20的Kaiser窗,且具有更窄的主瓣宽度,说明调节因子β=11的Kaiser窗经过一阶自卷积改造后,在不影响频率分辨率的情况下取得了更好的频谱泄漏抑制能力,足以满足目前的谐波检测要求。因此,为平衡频率分辨率和旁瓣性能,折中选择调节因子β=11的Kaiser窗作为自卷积运算的母窗函数。
理论上可以通过更高阶的自卷积运算提高窗函数的旁瓣性能,但高阶的自卷积运算会导致运算数据的增加,比如二阶自卷积运算的数据将由原来的N点增加至3N-2个点,而且高阶的自卷积运算同样会导致窗函数主瓣宽度的增加[28];因此,综合考虑频谱泄漏的抑制能力、频率分辨能力以及全相位数据预处理算法的相位不变特性,选择一阶自卷积Kaiser窗(β=11)对谐波信号进行处理。
1.2 基于一阶自卷积Kaiser窗的DFT算法
对已知谐波原始信号s(n)均匀采样2N-1个点所得到的离散时间信号
(6)
式中:n=0,1,…,2N-2为采样序列;H为谐波项数;Ah为第h次谐波的幅值;φh为第h次谐波的初始相位;fs为采样频率;f1、A1、φ1分别为基波的频率、幅值、初相。
为抑制频谱泄漏,对s(n)加归一化卷积窗w*(n),并忽略负频点-hf1处信号的旁瓣干扰,得加窗后的DFT表达式
(7)
式中hf1=khΔf为第h次谐波的频率,Δf=fs/(2N-1)。
为简化推导,设第h次谐波为检测量,忽略频谱泄漏,故式(7)简化为
(8)
考虑到加权谱线数量的增多会导致计算量的增加,且已采用具有良好旁瓣性能的卷积窗函数加权抑制频谱泄漏,峰值谱线附近谱线幅值较小,采用过多加权谱线校正后精度提高不明显,故引入双谱线插值算法校正频率和幅值偏差,具体求解参照文献[29]。
依据双谱线插值算法可推导出第h次谐波的频率估计表达式
(9)
第h次谐波的幅值修正公式
(10)
式(9)、(10)中:L1=|S′(khaΔf)|、L2=|S′(khbΔf)|分别为靠近被测频点附近的最大谱线kha和次最大谱线khb的幅值,满足kha≤kh≤khb=kha+1;α=kh-kha-0.5,α∈[-0.5,0.5]。
为解决谱线插值校正算法的频率误差蔓延到相位检测问题,引入全相位数据预处理算法,具体计算过程参照文献[26],则式(8)经过全相位数据预处理算法后得到的APFFT频谱为
(11)
故第h次谐波的初相位
(12)
综上,式(9)、(10)和(12)构成了高精度稳定的谐波参数估计表达式,可求得各次谐波的频率、幅值和相位。
2 分频段谐波检测DFT算法
针对电力电子化电力系统谐波带宽情况,若各频段谐波的检测均采用同样的采样频率和采样窗宽数据,势必增加谐波检测的计算负担,故提出分频段谐波检测思想,即针对不同频段的谐波采用不同的采样频率和采样窗宽对信号进行一阶自卷积Kaiser窗的DFT算法分析。
本文采用的一阶自卷积Kaiser窗的分频段DFT算法的分析计算过程如下:
a)对原始谐波信号s(n)进行Nf个频段划分,并设置各频段采样频率fsi和采样窗宽dti,其中i∈Nf,i=1时为划分的最低频段。
b)利用一阶自卷积Kaiser窗的DFT算法,分析计算最低频段(i=1)的各次谐波分量的频率f′ij、幅值A′ij和相位φ′ij,其中j为各频段的谐波次数;
c)依据已分析频段的谐波分量信息,进行信号的时域重构:
(13)
d)求取下一频段(i+1频段)待检测信号的残余分量
Δsi(n)=s(n)-s′(n).
(14)
e)对Δsi(n)进行一阶自卷积Kaiser窗的DFT计算,求得相应频段内的谐波分量的频率f′ij、幅值A′ij和相位φ′ij。
f)重复过程c)—e),直至满足fmax∈fim,fim为第i频段的理论最高频率,fmax=max(f′ij)为第i频段检测结果中的最高频率。
一阶自卷积Kaiser窗的分频段DFT算法流程如图3所示。
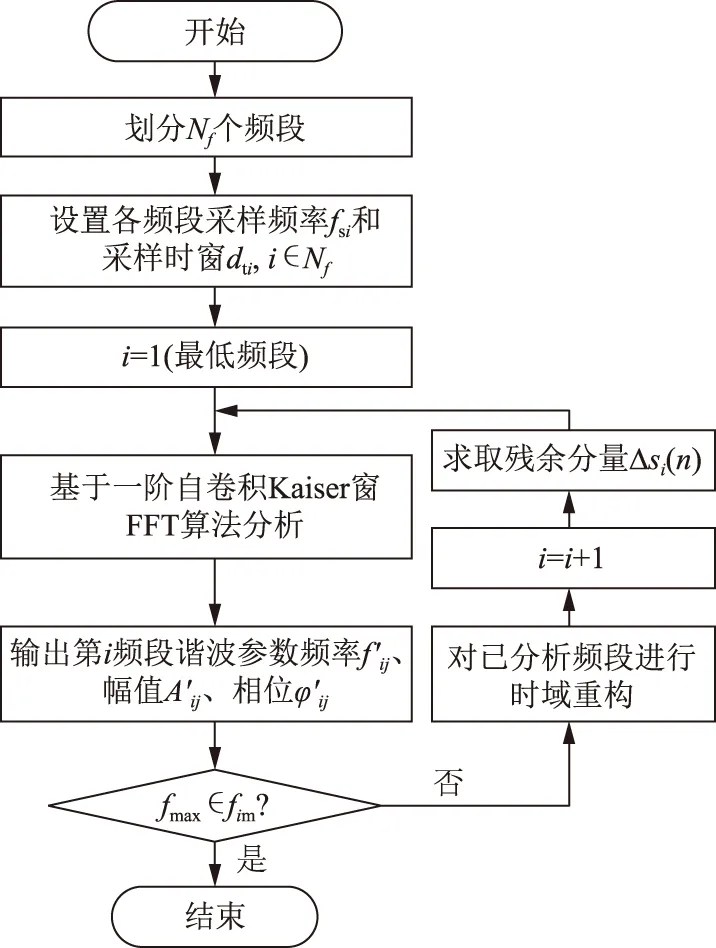
图3 分频段DFT算法流程Fig.3 Segmented DFT algorithm flow
由于电力电子化电力系统谐波检测带宽的要求已经扩展到50倍基频,且实际电网中以低频谐波成分为主[30],将50次谐波划分为高低2个频段;以1 000 Hz作为高低2个频段的分频点,故划分的低频段为[10 Hz,1 000 Hz],高频段为[950 Hz,2 500 Hz]。采样频率取fs=20 kHz、采样时间取1 s,并通过间隔数据二次采样形式降低各频段的采样频率。低高频段的划分及采样频率、采样点数的取值见表1。

表1 频段划分Tab.1 Frequency band segmentation
3 仿真分析
3.1 宽频信号谐波参数估计
为检验所提基于一阶自卷积Kaiser窗的分频段DFT算法对宽频信号谐波参数估计的有效性,构建50倍基频的多正弦基波和谐波的原始信号,其离散时间信号
n=0,1,…,2N-2.
(15)
式中:基波频率f1为50.2Hz;各频段的采样频率和采样点数见表1,给定仿真参数见表2。
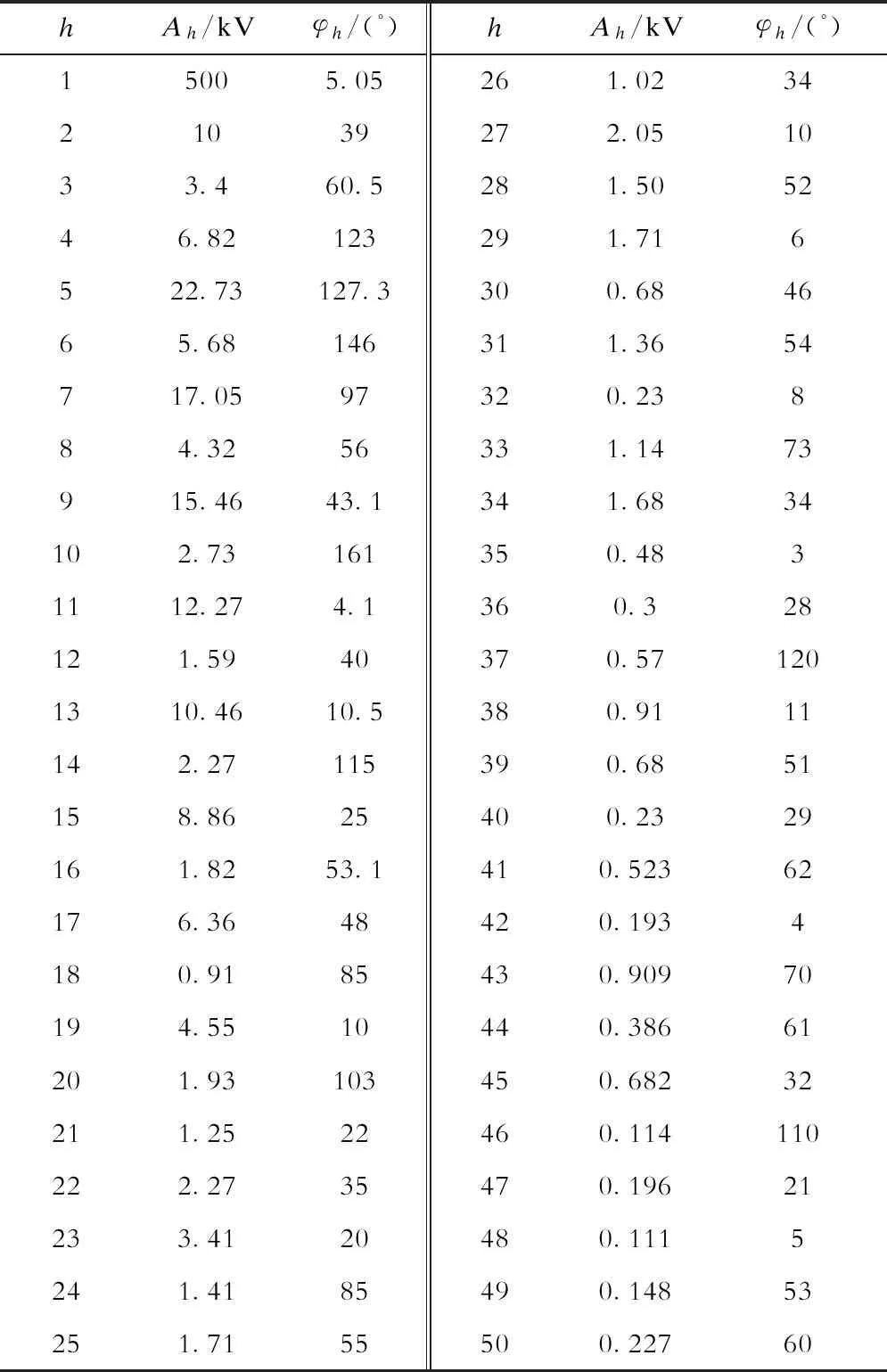
表2 给定仿真参数Tab.2 Given simulation parameters
仿真对比3种双谱线插值算法,分别为基于Kaiser窗(β=11) (算法1)、基于一阶自卷积Kaiser窗(β=11)(算法2)以及分频段一阶自卷积Kaiser窗 (算法3)。为确保仿真对比的有效性,算法1和算法2的采样点数与算法3一致,总共为2×(2N-1)=3 198个点,采样频率和原始数据的采样频率fs一样为20 kHz。各次谐波频率、幅值和相位相对误差分别如图4—图6所示。
由图4—图5可知,经过一阶自卷积运算的算法2和算法3的频率和幅值的检测精度较算法1高,这说明相同条件下通过自卷积运算能够提高Kaiser窗函数的旁瓣性能,进而提高抑制频谱泄漏能力。由图6可知,经过全相位数据预处理的算法2和算法3的相位估计精度总体达到10-7,而算法1的相位估计精度较低,这说明全相位数据预处理算法能够解决谱线插值算法的频率误差累计到相位检测误差中的问题。另外由图4—图6可知,基于分频段的算法3总体精度不及算法2,但仍具有较高的检测精度,这说明在算法2的基础上对原始宽频信号进行分频段的处理是可行的,但会产生一定的理论误差。
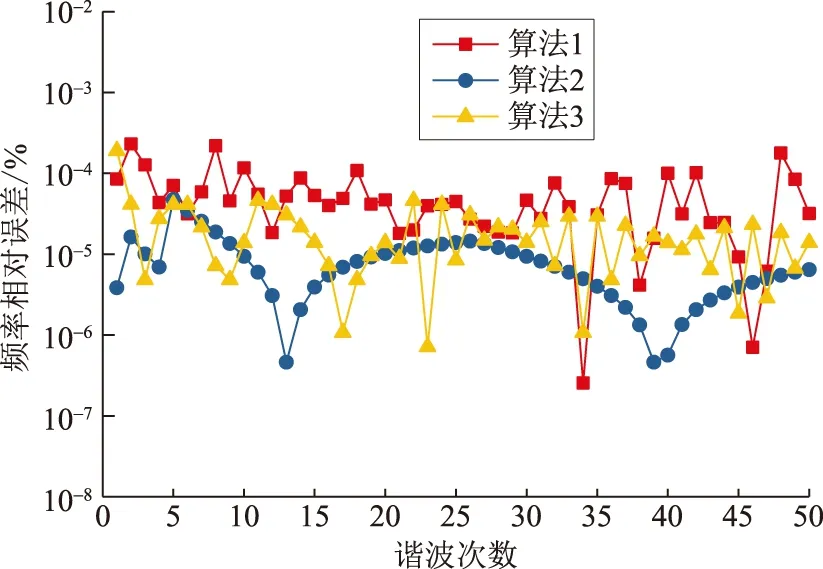
图4 频率估计值相对误差Fig.4 Relative errors of frequencies

图5 幅值估计值相对误差Fig.5 Relative errors of amplitudes

图6 相位估计值相对误差Fig.6 Relative errors of phases
为了分析所提分频段的谐波检测思路对减轻计算负担的有效性,将算法3的计算时间与算法1和算法2进行比较,计算机处理器为Intel(R)i5-4210M,主频为2.6 GHz。算法1、算法2和算法3在MATLAB软件中的计算时间分别为0.039 s、0.095 s、0.079 s。可见,算法2由于包括一阶自卷积运算和全相位数据预处理运算,计算时间有所增加。另外,算法3是在算法2的基础上对宽频信号进行分频段处理,计算负担有所下降。
3.2 基频波动
当采样频率fs恰好是基波频率f1的整数倍时,实现同步采样,此时谐波检测算法具有低的频谱泄漏和栅栏效应;但是电网基波频率时刻波动,基波频率波动会导致非同步采样,从而加剧频谱泄漏和栅栏效应,尤其在发生故障时,对谐波参数估计会造成较大影响。对3种算法抗基波波动的性能进行仿真实验,设基波频率以0.1 Hz的步差在49.5~50.5 Hz区间内变化[31],采样频率及其他参数同3.1节。据此获得的基波频率估计值相对误差如图7所示,各次谐波的频率、幅值及相位的相对误差分布分别如图8—图16所示。

图7 基波频率估计值相对误差Fig.7 Relative errors of fundamental frequencies

图8 算法1频率估计值相对误差Fig.8 Relative errors of frequencies of algorithm 1
由图7可知,基波频率发生波动时,3种算法检测基波都有较高的精度,但是算法2和算法3比算法1的检测精度高,说明一阶自卷积运算提高了窗函数旁瓣性能。算法3是在算法2的基础上对原始宽频信号进行分频段处理,进而对谐波信号进行检测,由图7可见算法3的检测精度略微低于算法2,但高于算法1,表明分频段处理是可行的且对基波波动的干扰影响不大。

图9 算法2频率估计值相对误差Fig.9 Relative errors of frequencies of algorithm 2
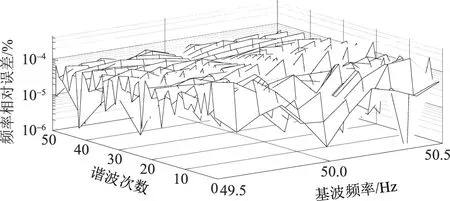
图10 算法3频率估计值相对误差Fig.10 Relative errors of frequencies of algorithm 3

图11 算法1幅值估计值相对误差Fig.11 Relative errors of amplitudes of algorithm 1
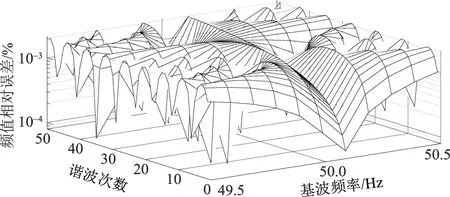
图12 算法2幅值估计值相对误差Fig.12 Relative errors of amplitudes of algorithm 2
由图8—图13知,在基波频率波动的情况下,算法2和算法3的谐波检测精度较算法1更高。尽管算法3检测精度较算法2略微降低,但仍然具有良好的抗基波波动干扰性能。

图13 算法3幅值估计值相对误差Fig.13 Relative errors of amplitudes of algorithm 3
由图14—图16可见,算法1在基波频率波动时,相位检测的性能明显低于其他2种算法,而经过全相位数据预处理算法改进得到的算法2和算法3具有良好的检测精度;算法3引入分频段产生的细微理论误差,使其相位检测精度略低于算法2。

图14 算法1相位估计值相对误差Fig.14 Relative errors of phases of algorithm 1

图15 算法2相位估计值相对误差Fig.15 Relative errors of phases of algorithm 2
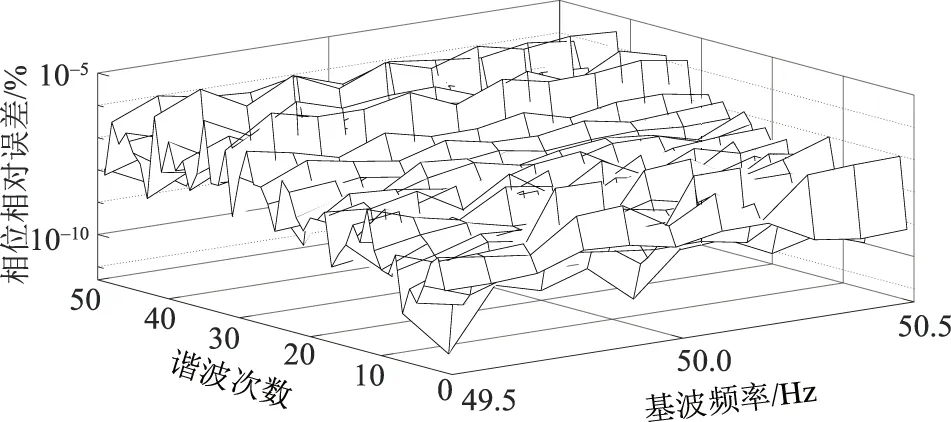
图16 算法3相位估计值相对误差Fig.16 Relative errors of phases of algorithm 3
3.3 白噪声干扰
实际电网中,噪声不可避免,且以高斯白噪声为主,主网信噪比通常为60 ~80 dB,低压配电网通常为60 dB,最小可达到45 dB[32]。随着电力系统电力电子化,噪声愈加复杂,将影响谐波参数的测量;因此,有必要进行更低信噪比的仿真实验以验证算法的抗噪性能,故给定信噪比为30 dB的高斯白噪声环境,对比3种算法的抗噪性能,仿真参数同3.1节,各次谐波频率、幅值和相位估计值的相对误差如图17—19图所示。
由图17—图19可见,在信噪比为30dB的强白噪声干扰下,经一阶自卷积运算的算法2较算法1具有较高的检测精度,尤其是相位精度;算法3是在算法2的基础上进行分频段处理,在噪声干扰下精度有所下降,但是下降不明显,仍具有较高的稳定性。

图17 噪声背景下频率相对误差Fig.17 Relative frequency errors in noisy environment

图18 噪声背景下幅值相对误差Fig.18 Relative errors of amplitudes in noisy environment
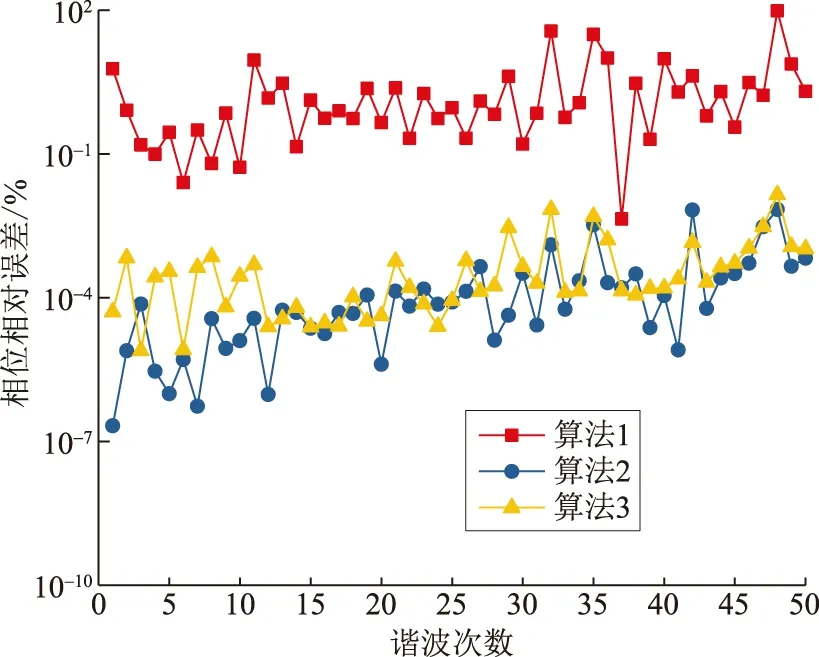
图19 噪声背景下相位相对误差Fig.19 Relative errors of phases in noisy environment
4 结论
基于电力电子化电力系统宽频谐波特性背景,提出基于一阶自卷积Kaiser窗的分频段谐波检测DFT算法,结论如下:
a)一阶自卷积运算能够在不改变Kaiser窗主瓣宽度的情况下进一步降低旁瓣峰值和加快旁瓣衰减速度。
b)一阶自卷积运算会导致运算数据由原来的N个点增加至2N-1个点,但能实现谱线插值算法和全相位数据预处理算法的优势互补,可以在不明显增加计算负担的情况下提供较好的频率、幅值和相位的检测精度。
c)分频段谐波检测思路对宽频信号的检测具有可行性,能在一定程度上降低计算负担,但会因为引入理论误差而导致检测精度略微降低。
d)所提分频段算法适合宽频信号检测,能有效克服基波频率波动和噪声干扰,谐波参数检测精度高且具有较高的稳定性和较低的计算负担。
本文未能实现Kaiser窗的调整因子β自适应调节,另外没有给出通用的频段选择原则和自动的实现方式。
