基于深度学习的中长期风电发电量预测方法

2021-07-02朱尤成王金荣徐坚

广东电力 2021年6期

朱尤成,王金荣,徐坚

(国电电力云南新能源开发有限公司，云南昆明 650051)

风电的开发利用可减少温室气体排放，减轻环境污染，缓解当前的能源危机[1-2]。由于风电具有强随机性和间歇性[3],风速等影响风电功率的因素随时间呈现无规律的变化,导致风电功率难以预测[4]。而对风电功率的准确预测不仅是解决风电消纳的重要手段，也会增强风电在电力市场中的竞争力。因此,准确的风电预测对于确定合理的调度计划和确保电网安全经济运行具有重要意义。

针对此类问题，国内外已有大量研究。从时间尺度上，可以分为超短期预测(以小时为单位，预测接下来0～4 h的发电功率)，短期预测(以日为单位，预测72 h内的电力输出)，中长期预测(以月或年为单位)。其中超短期预测主要用于风电系统的实时调度，短期预测主要用于制订电网的发电计划，中长期预测用于安排大型检修，而长期预测的主要作用是风电场选址评估。对于超短期预测的工作，文献[5]提出了一种结合卷积神经网络(convolutional neural network,CNN)和门控循环单元(gated recurrent units,GRU)网络的超短期风电预测模型，针对时间序列进行动态时序建模，完成对风电功率的超短期预测；文献[6]建立了一个基于离散马尔可夫链的超短期风电预测模型。对于短期预测的工作[7-9]，文献[9]利用宜昌市历史气象数据、电力负荷数据以及日期类型数据等建立长短期记忆(long short term memories,LSTM)网络模型，通过逐步调优试验评估，提出适用于宜昌电力负荷预测的LSTM网络模型方案。目前，很少有针对中长期时间尺度上的研究，一方面由于中长期风电预测应用场景偏少，仅在少量研究文献中有所提及[10-11]，另一方面我国风电场的发电量、气象等数据通常只可追溯至前5～7年[7-9]，这将导致中长期预测缺少充足的样本[10,12-14]。文献[15]建立了基于自适应小波神经网络的长期风力发电预测模型。

针对目前中长期风电预测中样本稀疏、缺乏通用特征表达框架、无法解决长期依赖时间序列的问题，本文工作如下：①使用来自不同地区4个风电场的特征数据，在研究适用于云贵高原地区风力发电预测模型的背景下，最大限度扩充模型数据集，为更好的训练模型、增强模型鲁棒性打下基础；②提出一种基于关联结构函数与神经网络的特征表示与融合方法，以有效表达风电场气象因素、地理位置等特征；③提出一种基于LSTM的中长期发电量预测模型，以有效解决模型对风电场时间序列数据反向传播时，早期月度数据信息缺失的问题；④最后对提出的多维特征提取(feature extraction，FE)-关联函数(copula，CO)-LSTM(FE-CO-LSTM)融合模型进行验证。

1 风电预测模型介绍

1.1 气象特征分析

影响风力发电量的气象因素众多且复杂，影响因素也各不相同。提高风电预测精度的关键之一便是有效提取气象主要特征，风电预测中气象特征主要包括：风力、气压、温度、湿度。已有的气象特征分析可以在一定程度上量化气象因素和风力发电之间的相关性，但这些基于线性相关系数的方法在实际情况下效果不佳，因为大多数气象因素以非线性方式与风力发电相关。我们使用基于关联结构的方法来表示气象变量与风力发电之间的非线性关系，以提取关键的气象因素，进行后续的中长期预测建模。

令连续随机变量X和Y分别表示气象数据与历史风电功率，其边际分布为F(x)和G(y)，并且相应的关联结构函数为C(u,v)，其中u代表边际分布F(x)，v代表边际分布G(y)。Kendall等级相关系数τ的定义为

(1)

根据Spearman等级相关系数ρs的定义[16]，使用Copula理论来计算ρs，

(2)

式中Ι=[0,1] 。上尾部相关系数λup与下尾部相关系数λlo的定义如下：

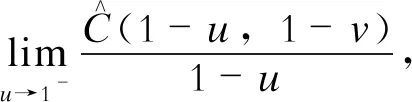
(3)

(4)

(5)

Kendall等级相关系数和Spearman等级相关系数反映了随机变量X和Y的一致性程度，并且在严格单调变换之后保持不变。它们的大小与X和Y的边际分布无关，这表明与线性相关系数相比，非线性相关系数的应用范围将会更广。尾部相关系数测量随机变量X和Y同时增加或减少的概率。

在气象特征分析模型中，使用核密度估计(kernel density estimation)方法评估气象数据与历史风电功率的边际分布〔对应上文中的F(x)和G(y)〕，使用关联结构函数分别计算上述4种气象数据与历史风电功率的相关性，将其结果作为各气象特征在神经网络特征融合模型中的初始权重。具体步骤为：①使用关联结构函数建立风速和风电功率的联合分布模型，并采用最大似然估计法(maximum likelihood estimation，MLE)来估计模型的参数；②计算关联结构函数的Kendall和Spearman等级相关系数；③计算风速与风电功率的尾部相关特征，根据4种气象特征分别和风电功率的尾部相关系数，确定特征在神经网络模型中的初始权重。

1.2 基于多层感知机的多特征的融合表示

影响风电发电量的因素是多方向性的，机组在正常运行状态由于受到天气和人为因素的影响，会使得实际发电量与理论相比存在差别，因此本文将具体分析影响机组发电量的主要因素，包括风能潜力、气温、气压信息、空气湿度、日期和海拔。其中使用有效风能密度、风能大小和空气密度ρ表示风能潜力特征，定义有效风能密度

(6)

式中：N为各等级风速出现的总次数；vi为i等级的风速；Ni为等级风速vi出现的次数。

空气的湿度可以用空气中所含水蒸汽的密度，即单位体积的空气中所含水蒸汽的质量来表示。由于直接测量空气中水蒸汽的密度比较困难，而水蒸汽的压强随水蒸汽密度的增大而增大，所以通常用空气中水蒸汽的压强来表示空气的湿度。令E为水气压，定义相对湿度

(7)

式中Ew为纯水平液面饱和水气压。Ew的计算公式为

(8)

式中：T为绝对温度；T1为水的三相点绝对温度。

气温为风电场全年的气温统计数据，海拔数据是风电场建设处海拔高度，二者均为统计数据。

模型的核心思想是使用每日的风力信息、气温信息、气压信息、空气湿度和风电场的海拔信息，预测月度和年度发电量。模型具体实现步骤为：

a)将采集自气象站和风电场区域的气象信息等多维日度数据进行嵌入表示，构造日度特征向量。

b)通过神经网络以月为单位将日度特征向量表示为月度特征向量，融合网络对日度特征集融合过程为

(9)

式中：ci,P为特征P的月度向量表示，i表示月份；wj,P为特征P的日度向量表示，j为当月日期数；D为当月的总天数；αij为神经网络中日度特征向量的权重向量，其中4种气象特征初始权重由1.1节计算得到的相关系数表示。

c)对多维月度特征进行向量表示，表示过程如图1所示。其中：风能潜力特征由有效风能密度、风能大小和空气密度表示；空气湿度特征由空气绝对湿度表示；月度气压特征、气温与海拔特征则使用当地当时的统计信息。多种月度特征长度不一、形式差异较大，因此首先将其表示为可变长度的低维向量。

图1 风电场特征融合模型图Fig.1 The framework of wind farm feature fusion model

d)初始化多层感知机(multilayer perceptron,MLP)网络，包含1个输入层、1个隐藏层和1个输出层，均为全连接网络。MLP网络接受低维月度特征向量，输出结构统一的高维特征向量。然后将各类高维月度特征向量进行拼接，构成风电场当月融合特征向量表达，为后续LSTM模型的中长期发电量预测做准备。

1.2 基于LSTM的预测模型

LSTM神经网络具有长期记忆功能，可以有效利用有限数据样本的长期依赖性[17-18]。它还可以解决递归神经网络(recurrent neural network,RNN)训练过程中梯度消失导致失去感知远距离网络单元能力的问题。主要思想是使用特殊的神经元长时间存储和传输信息，以获得永久性记忆、捕获长期依赖性、减缓时间序列中信息损失的速度以及增加深度计算的优势。LSTM神经网络可以深入评估有限数据样本中的长期依存关系和趋势关系，适用于数据样本有限的中长期风力发电预测。

LSTM网络结构图如图2所示。

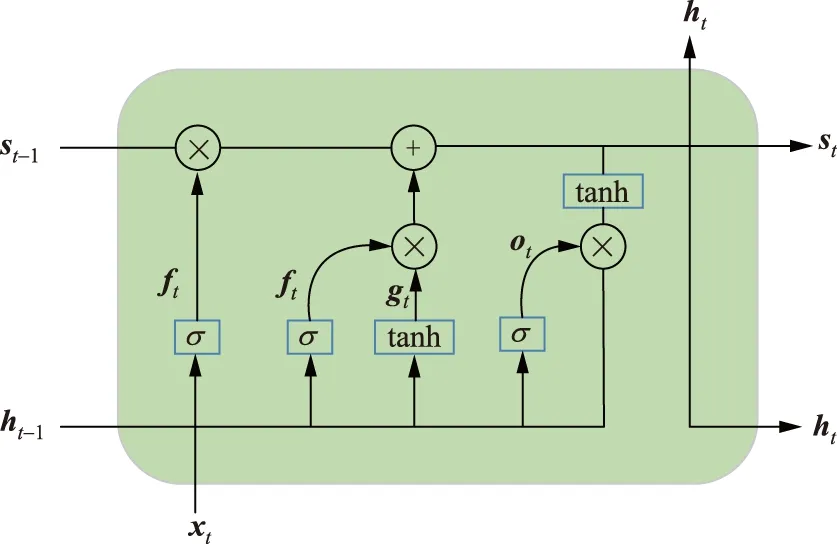
图2 LSTM网络模型Fig.2 Long and short term memory network model

图2中：

(10)

LSTM预测模型基于风电月度特征融合向量，进行月度风电发电量预测。这一过程可以表示为

[h(t+1)h(t+2) …h(t+12)]=FLSTM(h(t),

h(t-1),…,h(t-n),x(t),

x(t-1),…,x(t-n)).

(11)

式中：h(t+1)为当前时刻的预测结果；[h(t+1)h(t+2) …h(t+12)]为当前12个月发电量的预测向量；h(t),h(t-1),…,h(t-n)为先前时刻的月度发电量预测结果；x(t),x(t-1),…,x(t-n)为先前时刻的输入，即月度特征融合向量；n为当前已输入的网络节点数。

2 实验与结果分析

本文首先对风电场原始数据进行日度特征提取，进而对整个网络模型(包括风电场月度特征融合模型和发电量预测模型)进行训练，最终得到训练好的预测模型。具体流程如图3所示。

图3 FE-CO-LSTM模型流程Fig.3 Flow chart of the FE-CO-LSTM model

2.1 数据集与对比模型

考虑到中长期风电预测问题缺乏大样本集，从而导致模型预测精度较低，本文收集了我国云南和贵州共计4个风电场5～7年的发电历史记录，以及相应时间段内该地区的风力、气压、湿度、气温和海拔信息，数据集具体统计情况见表1。其中，将数据中的月度信息作为网络中时间序列的一个节点输入，由表1可见，数据集中收集的风电场数据的时间跨度不同，因此各数据集下网络的长度并不相同。云南风电场1与贵州风电场1为高原地区风电场，其数据集具有完整风力、气压、气温、湿度、海拔数据。云南风场2和贵州风场2数据集分别有湿度数据和风力数据的缺失，在模型特征融合时仍使用相同方法。

表1 4个风电场数据集信息Tab.1 Data set information of four wind farms

为验证模型的有效性，本文选取了基于支持向量机(support vector machines,SVM)风电预测方法[19]、基于CNN的风电预测方法[20]、LSTM(CO)方法(仅使用气象特征分析和LSTM的网络模型)与LSTM(FE)方法[21](基于特征融合方法与LSTM的网络模型)作为对比。

2.2 实验与结果分析

为评估中长期风电发电量预测模型的准确性，使用2个指标作为评估标准：一是平均绝对百分比误差(mean absolute percentage error，MAPE)KMAPE用于评估实时误差，另一个是均方根百分比误差(root mean squared percentage error，RMSPE)KRMSPE用于评估预测期间的总体误差。2个指标的计算式为：

(12)

(13)

式(12)、(13)中：W′i为每月发电量的预测值；Wi为每月的真实发电量;m为预测的总月份数。

在4个风电场的数据集中，将最后一年的数据作为测试集，其余作为训练集。模型对测试集的预测结果如图4所示，预测误差统计见表2。

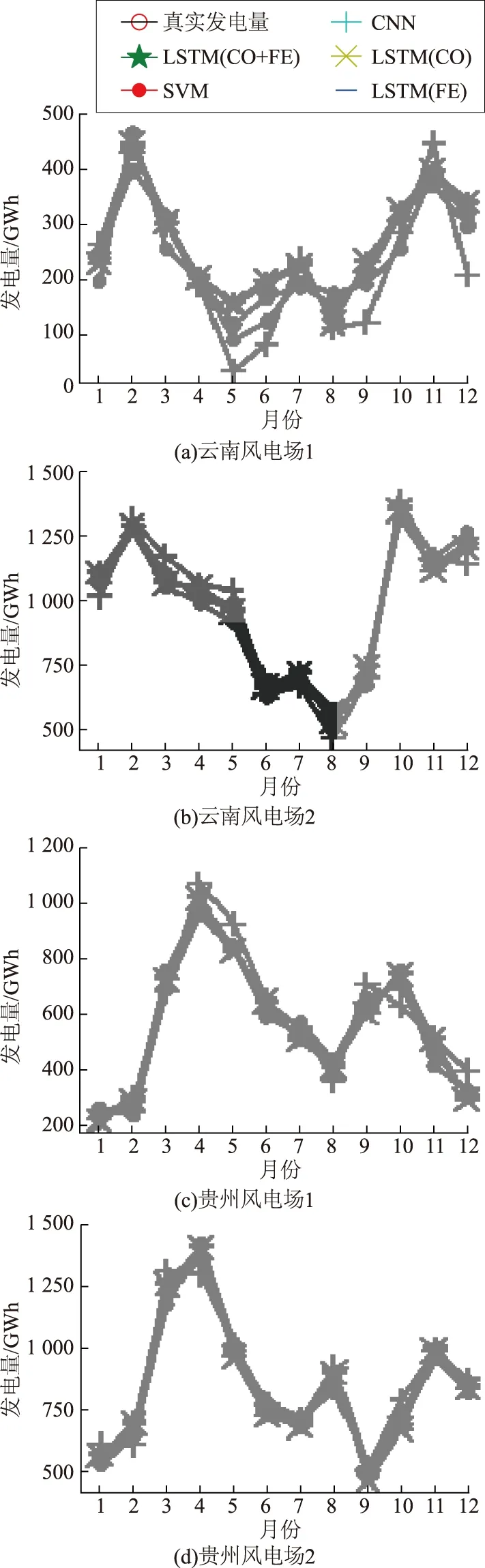
图4 5种预测模型的实验对比Fig.4 Experimental comparisons of 5 prediction models

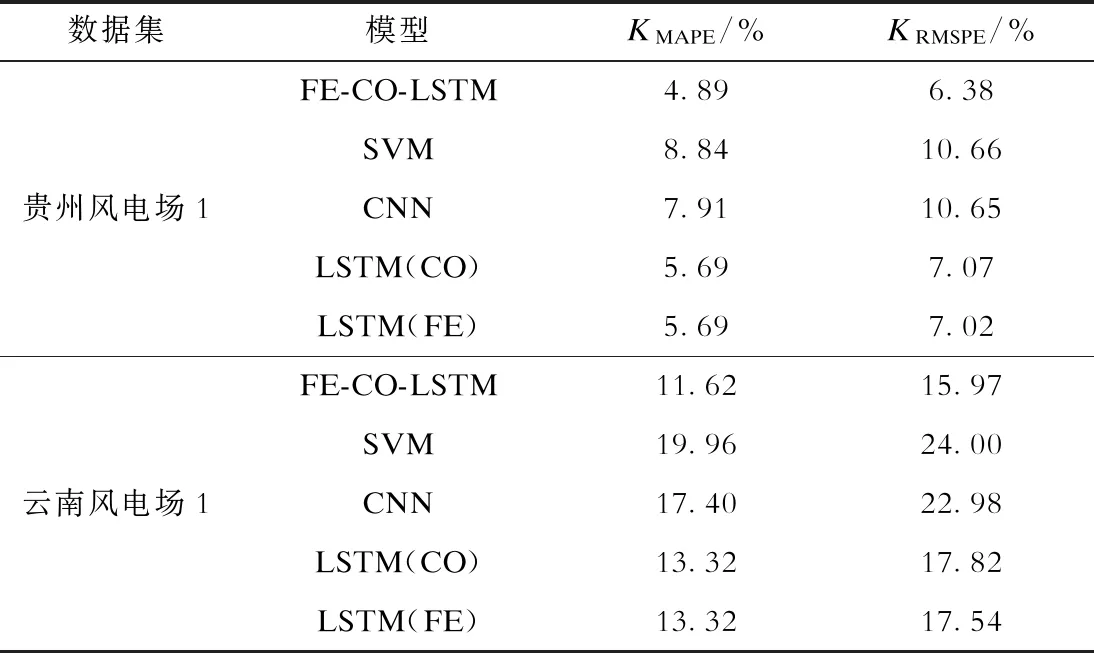
表2 FE-CO-LSTM模型与其他模型预测误差统计Tab.2 Prediction error statistics of the FE-CO-LSTM model and other models

表2列出了贵州风电场1、云南风电场1的实验结果，进一步证明了本文方法的有效性。通过观察可知：①FE-CO-LSTM、LSTM(CO)和LSTM(FE)这3种基于LSTM的方法相比SVM、CNN方法大幅减小了误差；②CNN模型在云南更高海拔地区的风电场1数据集上表现出比SVM模型更小的误差，说明对于高原地区高海拔、低气压、风密度低且风向变化频繁的复杂数据，神经网络模型可以学习到更好的特征表达；③LSTM(CO)、LSTM(FE)方法的误差与FE-CO-LSTM方法相比均有所上升，这说明气压-发电量相关度表示与多维度特征融合在LSTM模型中起到提高模型精度的作用。