不同结构的左旋聚乳酸冠脉支架的力学行为研究

2021-07-02张园园颜文涛李建军王盛章

生物医学工程学进展 2021年2期

张园园，颜文涛，李建军，王盛章，

1.复旦大学工程与应用技术研究院生物医学工程技术研究所(上海, 200433)

2.复旦大学航空航天系生物力学研究所(上海, 200433)

0 引言

随着介入治疗技术的发展，经皮冠状动脉介入治疗技术已经经历了从球囊血管成形术到金属裸支架、药物洗脱支架的发展［1-2］。但永久性金属支架如不锈钢支架、钴铬合金支架等在人体血管中的长期存在，会引起炎症反应，导致内膜增生、支架晚期血栓等一系列不良后果［3-5］。在这种情况下，全降解支架应运而生。由于这类支架植入人体后可以在一定时间内降解，具有可以避免再狭窄、晚期血栓风险等优点［6-8］，已逐渐成为国内外医疗器械领域研究人员关注的热点。然而，全降解支架存在支撑性能严重不足，在使用过程中容易断裂的问题，阻碍了其在临床治疗中的广泛应用［9］。但是到目前为止系统地研究全降解支架结构尺寸与力学性能之间内在联系的文章还相对较少。

利用有限元仿真和样品实验的方法系统地研究了不同的结构尺寸下左旋聚乳酸支架在使用过程中的应变分布、回弹率和径向位移等参数的变化，从而评价支架尺寸对其回弹大小和径向支撑性能的影响，为全降解支架设计和优化时如何选择支架加工管材直径提供一定的思路和参考。

1 体外实验材料与方法

选用的支架材料为左旋聚乳酸，经过激光切割的方法得到经典的Multilink结构［10］。支架单元的杆宽和壁厚均为0.15 mm，一周为6个支架单元。对比实验选择外径尺寸分别为1.8 mm、2.9 mm、3.3 mm的三种支架，为方便叙述，依次分别记为A、B、C结构。

支架的压握回弹率和扩张回弹率根据公式(1)、(2)进行计算。最后，使用支架径向力测试装置对扩张完毕后的支架样品进行径向力的测试。

2 有限元方法

利用有限元仿真来分析支架的力学行为是一种非常高效的方法，因此建立可降解冠脉支架三维模型，模拟支架实验中压握、压握回弹、扩张、扩张回弹和支撑力测试的整个过程，通过分析不同支架结构在各个阶段的应变分布、回弹率以及径向位移的变化来评价支架的回弹大小和支撑力。

2.1 几何模型和网格划分

三维建模时，参考体外样品实验时选用的A、B、C三种支架的结构尺寸进行设置。采用Abaqus 6.14.1软件中的隐式分析进行计算，如图1所示为B结构支架的三维图。综合考虑计算精度和时间成本，采用六面体网格对模型进行网格划分，支架模型网格类型为C3D8I非协调单元，A、B、C三种结构的网格数量分别为20 688个、26 020个和25 860个。

图1 B结构支架的三维图Fig.1 3-D drawing of B stent

仅模拟支架的体外实验，不考虑血管和斑块对支架的影响，因此把支架压握工具和球囊扩张工具都简化成刚性圆筒，采用SFM3D4F单元建模，模拟时通过控制刚性圆筒的直径变化来实现支架的压握和扩张［11］，A结构有限元模型，如图2所示。最后对支架外表面施加一个100 kPa的径向压力模拟血管外载荷的作用，通过计算支架在该压力下的径向位移来考察支架的支撑力大小。由于支架均为对称结构，为节约计算成本，在圆周方向取1/3，轴向取4个单元节段进行模拟，如图3所示。图4为支架的载荷历史。

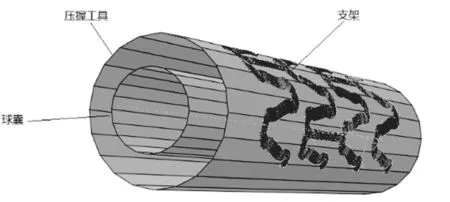
图2 A结构有限元模型Fig.2 A Stent FE model

图3 三种外径管材支架的三维图Fig.3 3D stent drawing of different structure

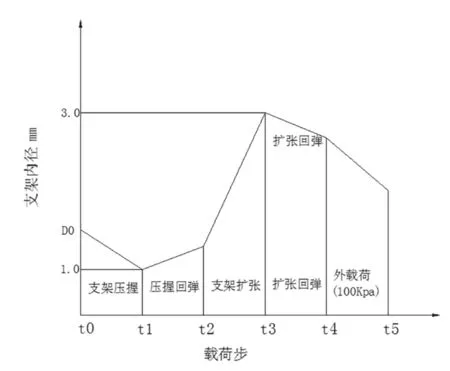
图4 支架加载历史Fig.4 Loading History of stent

2.2 材料模型

选用的可降解支架材料为左旋聚乳酸（PLLA），材料模型为非线性的弹塑性模型，其弹性模量为3.1 Gpa，泊松比为0.3，拉伸断裂极限为13%。采用各向同性Mises屈服准则来表征左旋聚乳酸材料的力学行为［12］。

2.3 边界条件

分析过程中，为了防止发生刚体位移，在支架的一端约束柱坐标下的Z向位移，同时在周向的对称面上施加对称约束。

3 结果

塑性应变、回弹率和径向支撑力是评价支架力学性能的三个重要参数，因此，对有限元仿真得到的数据进行后处理并和体外样品实验得到的结果进行比较来研究左旋聚乳酸支架的不同结构对其塑性变形、回弹大小和径向支撑性能的影响。

3.1 应变分析

有限元模拟三种不同结构的左旋聚乳酸支架压握到1.3 mm外径以及扩张到3.0 mm内径后的等效塑性应变分布分别如图5、6所示，结果显示：

图5 三种左旋聚乳酸支架压握后等效塑性应变分布图Fig.5 Equivalent plastic strain distribution of 3 crimping PLLA stent

（1）最大塑性应变分布在圆弧位置附近，而连接杆和支架杆未发生明显的塑性变形；

（2）随着管材直径的增加，支架塑性变形的区域和幅值都增大。

实验完成后，B、C两种结构左旋聚乳酸支架的压握后形态如图7所示，可见支架圆弧位置内表面处有轻微凸起，而外表面却不明显，且直径较大的C结构比B结构凸起更明显；B、C两种结构左旋聚乳酸支架扩张后的形态如图8所示。实验结果表明，在塑性变形最大的圆弧位置均未出现裂纹，但C结构支架的圆弧内表面有黑色线状印记产生（B结构支架则不明显）。表明直径较大的C结构支架塑性变形比B支架严重。

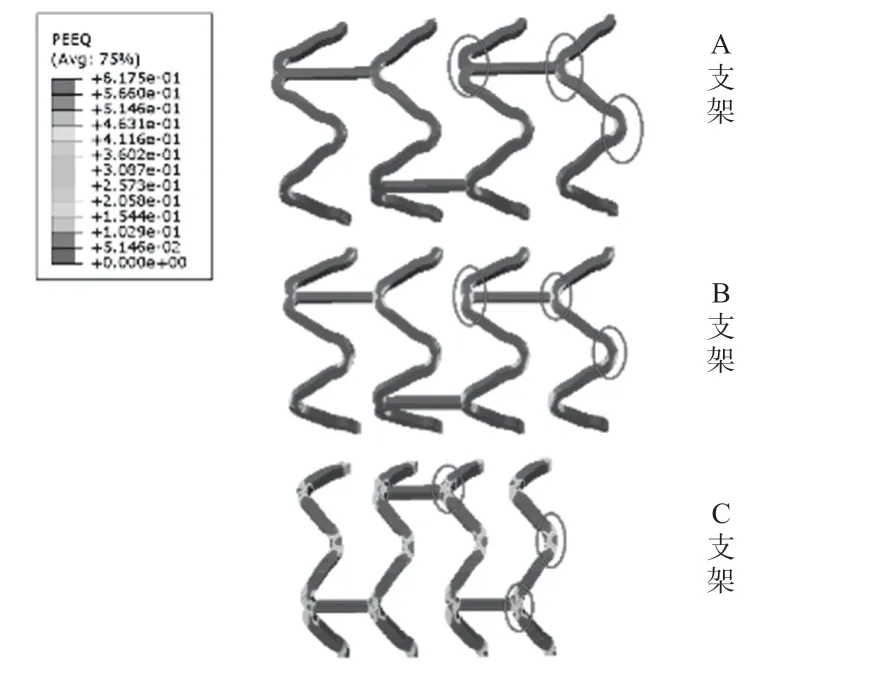
图6 三种结构左旋聚乳酸支架扩张到3.0 mm内径后等效塑性应变分布图Fig.6 Equivalent plastic strain distribution of 3 PLLA stent after expanding to 3.0 mm ID

图7 压握形态(50x)Fig.7 Crimping state(50x)

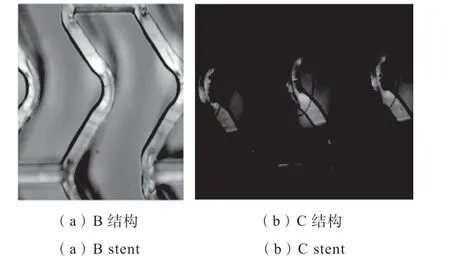
图8 扩张形态图（放大50×）Fig.8 Expanding state(50×)

3.2 压握回弹与扩张回弹分析

根据公式（1）、（2）得到三种不同结构左旋聚乳酸支架压握回弹率和扩张回弹率的有限元模拟结果和实验结果，见表1与表2。从表中可以看出，实验结果与数值模拟结果呈现的规律相吻合，即：随着管材直径的增加，压握回弹率和扩张回弹率均随之减小，C结构的回弹最小。

表1 左旋聚乳酸支架压握回弹率和压握回弹后直径Tab. 1 Crimping recoil and diameter of PLLA stent after recoil

表2 左旋聚乳酸支架扩张回弹率和扩张回弹后支架直径Tab. 2 Expanding recoil and diameter of PLLA stent after recoil

3.3 支撑力分析

支撑力分析结果表明，随着管材直径的增加，径向位移减小，即径向支撑力提高，见表3。

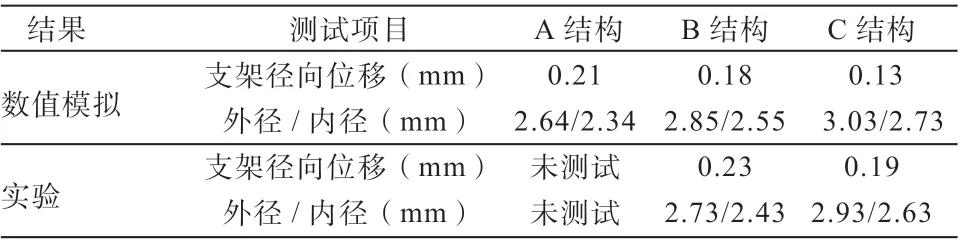
表3 左旋聚乳酸支架在100 kPa压力载荷下的位移Tab. 3 PLLA Stent displacement under 100 kpa pressure

B、C支架结构对应的外径-径向支撑力曲线实验结果如图9所示，可见C结构支架较B结构支撑力更大。实验结果与数值模拟结果基本一致，且两者差值均在2%以内，说明有限元法可以用来评价支架的支撑力性能。

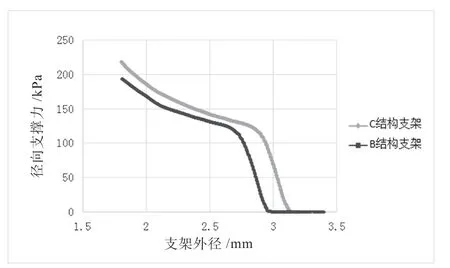
图9 支架的径向支撑力曲线Fig.9 Radial force curve of PLLA stent

4 讨论

通过数值模拟和实验结果分析可知：支架压握后，A结构支架圆弧段大部分位置处于弹性范围内，仅很小的区域发生了塑性变形，因此其压握回弹最大。而C结构支架圆弧位置几乎全部发生了塑性变形，其压握回弹率也最小。支架扩张后，B、C两种结构支架均未发生断裂现象，但B结构支架的扩张回弹较大。

而针对压握时支架内表面出现了轻微凸起，扩张后在C结构支架的圆弧内侧位置有黑色线状条形印记产生，但是并未观察到断裂现象，这是由于PLLA的玻璃化温度为60～65℃，而本研究压握机温度设置为50℃，因此压握时左旋聚乳酸材料在玻璃化温度附近发生软化，加之支架内表面支架杆之间的空隙更小，从而在支架内表面形成材料的柔性挤压堆积。在支架扩张后该位置处堆积的材料重新展开，所以并未出现支架结构的撕裂现象，这也解释了C支架在数值模拟时出现塑性应变远超材料最大拉伸应变（13%）的原因。