湖南省栎类次生林冠幅—胸径模型模拟研究
2021-07-02朱晋梅朱光玉杨琬珑王琢玙
朱晋梅,朱光玉,易 烜,杨琬珑,牟 村,王琢玙
(1.湖南省林业局,湖南 长沙 410004;2.中南林业科技大学,湖南 长沙 410004;3.湖南省青羊湖国有林场,湖南 宁乡 410627; 4.湖南省森林植物园,湖南 长沙 410004)
树冠是林木进行光合、呼吸以及蒸腾作用等一系列生理活动的主要场所。林木的生长发育健康与否,在很大程度上取决于林木树冠的形状和大小。同时,树木的长期竞争水平也能够通过树冠的生长状况进行反映[1-2]。冠幅是反映树冠结构最常用的指标,常被用来估算树冠表面积、树冠形状、林分郁闭度等重要变量;此外,冠幅也是林分模型拟合、林木可视化模拟的重要参数[3]。可以看出,冠幅在林业中的应用范围广泛、应用价值较高,但在实际调查过程中,对于分布范围广、面积大的林分,冠幅的测定往往会耗时耗力。因此,有必要建立精准有效的预测模型来预测冠幅。
目前,关于冠幅模型的构建主要包括简单模型[4-7]与广义模型[8-10](包括再参数化模型、含哑变量(固定效应)模型、混合效应模型等)两种。简单模型一般只含胸径1个自变量,而广义模型是由胸径和其他能够反映林木、林分间差异的林分变量、立地因子等生境因子构成。与简单模型相比,广义模型往往更适用于林分结构与立地条件复杂的天然林、混交林,能够表示复杂林分中的林木差异、林分以及立地效应。西班牙学者在西班牙北部地区建立了樟子松的冠幅模型[9]。董晨等[10]利用参数预估法构造了胸径和树高的参数化预估模型。符利勇等[11]建立了嵌套2水平非线性混合冠幅模型。符亚健[12]则利用协变量,将不同树木的多个林分因子作为协变量,构建了冠幅—胸径预测模型,使一直以来的东南西北四个方向的冠径与本身冠幅大小的相容性问题得到很好的解决。Sharma等[13-14]在样地水平对欧洲云杉(Piceaabies) 、欧洲山毛榉(Fagussylvatica) 等树种建立了混合模型,从而确定了各树种冠幅模型中相关因子和林分变量,并分析了其与冠幅大小的相关性。
栎类,是我国亚热带地区天然林的主要成分。第九次全国森林资源清查结果显示,栎类林的蓄积占全国的8.32%,面积占全国的9.21%,研究价值突出[15]。 栎类次生林是我国中亚热带一种典型的次生林群落类型。湖南省栎类资源丰富,分布广泛,是本省残存不多的天然阔叶林中的优势种[16-18]。湖南省栎类次生林的林分质量不高,林分竞争激烈。所以,建立湖南省栎类次生林胸径—冠幅的模型,研究林木胸径冠幅的相关关系,对于分析林分因子生长、林木竞争、提高林分质量等有重大意义。
1 材料与方法
1.1 资料的收集与整理
研究区分别为湖南省青羊湖国有林场(宁乡市)小蒿溪(QYH)、沅江市龙虎山国有林场场部(LHS)、中南林业科技大学芦头实验林场上山坪(LT)、桑植县八大公山国家级自然保护区天平山(TPS)和郴州市苏仙区五盖山国有林场黄金窝(WGS)。对在5个区域建立的51块样地进行数据采集,并设立标准地。5个区域样地基本情况见表1。每块样地中选取3株栎类优势木作为研究对象,这些优势木主要包括:亮叶水青冈(Faguslucida)、长叶石栎(Lithocarpusharlandii)、锥栗(Castaneahenryi)、甜槠(Castanopsiseyrei)、枹栎(Quercusserrata)、细叶青冈(Cyclobalanopsisgracilis)、多脉青冈(Cyclobalanopsismultinervis)、青冈(Cyclobalanopsisglauca)、大叶青冈(Cyclobalanopsisjenseniana)等9种栎类树种。实测各个标准地的多个林分结构因子,包括冠幅、优势木胸径、优势木高、林分类型、树种、林分密度、郁闭度等。所测量的151株树木中,剔除异常数据,留下146株作为最终整体数据。随机选取95株数据作为建模数据,51株数据作为检验数据(见表2)。
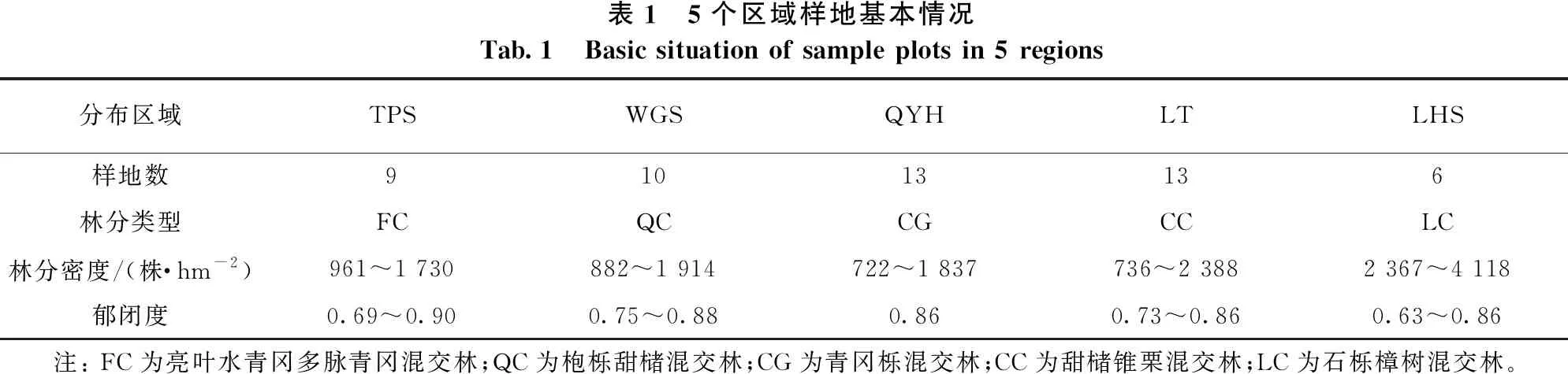
表1 5个区域样地基本情况Tab.1 Basic situation of sample plots in 5 regions分布区域TPSWGSQYHLTLHS样地数91013136林分类型FCQCCGCCLC林分密度/(株·hm-2)961~1 730882~1 914722~1 837736~2 3882 367~4 118郁闭度0.69~0.900.75~0.880.860.73~0.860.63~0.86 注: FC为亮叶水青冈多脉青冈混交林;QC为枹栎甜槠混交林;CG为青冈栎混交林;CC为甜槠锥栗混交林;LC为石栎樟树混交林。

表2 建模数据和检验数据统计信息Tab.2 Modeling data and test data statistics数据建模数据检验数据平均冠幅/m胸高胸径/cm优势木高/m平均冠幅/m胸高胸径/cm优势木高/m最小值1.0505.29.61.25010.410.2最大值6.32562.535.56.70063.530.2平均值3.03524.9115.823.0829.4516.68标准差1.1211.243.981.1313.524.32
本研究中的单木冠幅计算公式为:
CW=(CW东+CW西+CW南+CW北)/4
(1)
式中:CW为单木冠幅;CW东为东方向冠幅半径;CW西为西方向冠幅半径;CW南为南方向冠幅半径;CW北为北方向冠幅半径。
1.2 研究方法
本文以湖南省51块样地的栎类林数据为研究对象。首先,通过EXCEL 2010软件,输入胸径、冠幅的数值;然后,分样地计算每棵林木东西南北四个方向的平均冠幅,根据以往的研究成果选择几个合适的候选模型。 接下来,在ForStat软件中输入胸径和冠幅的数值,进行模型选择,筛选出精度较高、拟合效果最好的模型作为最后的冠幅—胸径模型。最后,把其他林分因子作为固定效应,分别加在不同参数上,进行模型优化。
1.2.1 基础模型选择 基础模型的选择直接影响冠幅—胸径模型拟合的结果。本文选用常用的5个冠幅—胸径模型作为湖南省栎类天然次生林单木冠幅模型的候选模型(见表 3)。对候选模型的模拟结果进行分析对比,选出最优模型。

表3 候选冠幅—胸径模型Tab.3 Candidate crown width-breast diameter model模型编号模型表达式模型类别1CW=a+b×D性函数Line2CW=a+b×D+c×D2 次型Quatriatic3CW=a× 1-b×exp -c×D 分子式Mitscherlich4CW=a×exp b×D 数函数Exponential5CW=a× 1-exp -b×D c理查德Richards 注:CW 为冠幅(m);D 为胸径(cm) ;a,b,c 为模型参数。
1.2.2 模型优化 除胸径外,其他林分因子也同样影响冠幅大小,如优势木高、树种、林分类型、林分密度等。在模型中加入林分变量增强冠幅—胸径之间的相关关系。在众多相关因子中,采用Forstat 2.2数量化方法I[19]模块分析各因子对湖南省栎类单木冠幅的影响,筛选出影响显著的主导因子,剔除影响不显著的因子,并将主导因子作为固定效应添加在基础模型参数上,构建含固定效应的冠幅—胸径模型,从而优化模型。
1.2.3 模型评价及检验 本文利用决定系数 (R2)、平均绝对误差(MAE)和均方根误差(RMSE)3 个指标对5个候选模型、各个含固定效应的冠幅—胸径模型进行比较和评价,选出最优候选模型(基础模型)及最优含固定效应的冠幅—胸径模型。当R2越大,拟合精度越大;当MAE和RMSE越小,拟合精度越高,说明模型拟合效果越好。各个评价指标计算如公式(2)(3)(4)所示。
R2=1-(SSE/TSS)=
(2)
(3)
(4)

2 结果与分析
2.1 模型选择
表4为5个候选模型的评价指标。其中,模型1为线性模型,模型2-5为非线性模型。R2越大,MAE和RMSE越小,说明模型的拟合能力越强。对各模型评价进行综合分析,得出模型2拟合效果最好的指标(见表4)。选择模型2为基础模型,其表达式见式(5)。
CW=1.257+0.096D-0.004D2
(5)
式中:CW为冠幅;D为胸径。
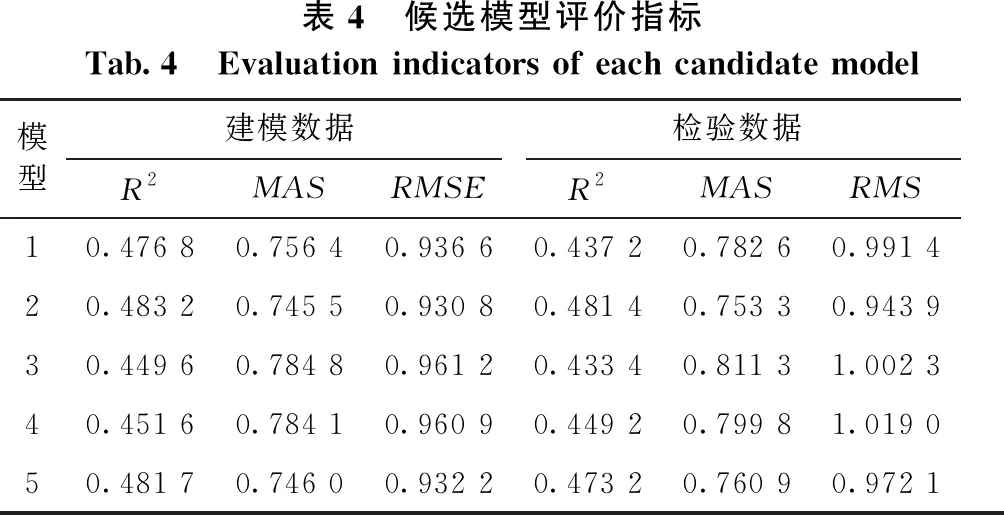
表4 候选模型评价指标Tab.4 Evaluation indicators of each candidate model模型建模数据检验数据R2MASRMSER2MASRMS10.476 80.756 40.936 60.437 20.782 60.991 420.483 20.745 50.930 80.481 40.753 30.943 930.449 60.784 80.961 20.433 40.811 31.002 340.451 60.784 10.960 90.449 20.799 81.019 050.481 70.746 00.932 20.473 20.760 90.972 1
2.2 模型改进
通过数量化方法I得到的优势木胸径、树种、优势木高、林分类型、林分密度中,除了优势木胸径外,仅有林分类型“Pr>F”=0.039 1小于0.05,即林分类型对冠幅有显著影响(见表5)。所以,把林分类型作为最终变量来构建湖南省栎类次生林胸径—冠幅模型。

表5 数量化方法I拟合结果Tab.5 Fitting results of quantitative method I因子组平方和自由度均方F值Pr>FLFLX4.324 722.162 43.318 10.039 1SZ2.654 260.442 40.678 80.667 0D29.695 0129.695 045.566 80.000 0H0.008 610.008 60.013 10.908 9LFMD0.042 410.042 40.065 00.799 1 注:LFLX为林分类型;SZ为树种;D为优势木胸径;H为优势木高;LFMD为林分密度。“Pr > F”值小于0.05则表示因子对冠幅(CW)影响显著。
将林分类型作为固定效应,分别加在模型2的参数a、b、c、a、bc、ac、abc上,对以上7种组合形式进行拟合分析,选取最优模型参数形式。模型拟合参数值和模型优化结果分别如表6、表7所示。从决定系数、平均绝对误差、均方根误差、冠幅实测值和预估值来看,在模型2参数c上添加树种因子固定效应结果最优,拟合效果最好(R2=0.774 3、MAE=0.648 7、RMSE=0.764 6)。最优模型为模型2.3,其最终表达见式(6)。

表6 含固定效应冠幅—胸径模型参数拟合值Tab.6 Parameter fitting value of crown width-DBH model with fixed effect参数名固定效应作用位置所对应的参数值abcabbcacabca.0.410 90.246 60.1969 0.945 40.156 80.620 8-2.031 6 a.LFLX_1-0.707 7-1.119 1-0.997 0-0.920 6 a.LFLX_20.600 9-0.431 2-0.019 71.909 1 a.LFLX_30.373 0-1.139 7-0.415 3-0.625 0 a.LFLX_4-0.278 5-1.1312-0.898 63.383 1 a.LFLX_50.000 00.000 00.000 00.000 0 b.0.14700.157 40.165 80.128 90.224 20.169 90.425 0b.LFLX_1-0.015 90.024 9-0.080 1-0.101 1 b.LFLX_20.021 20.044 7-0.024 9-0.209 6 b.LFLX_30.038 00.102 0-0.044 40.195 4 b.LFLX_4-0.004 40.039 7-0.093 6-0.376 3 b.LFLX_50.000 00.000 00.000 00.000 0
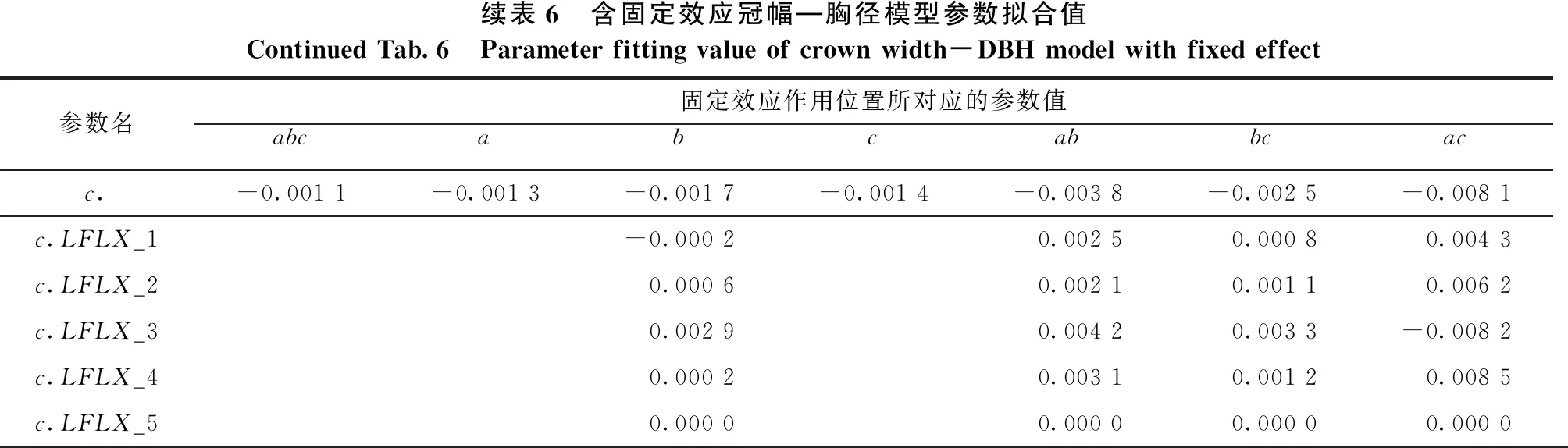
续表6 含固定效应冠幅—胸径模型参数拟合值Continued Tab.6 Parameter fitting value of crown width-DBH model with fixed effect参数名固定效应作用位置所对应的参数值abcabbcacabcc.-0.001 1-0.001 3-0.001 7-0.001 4-0.003 8-0.002 5-0.008 1 c.LFLX_1-0.000 20.002 50.000 80.004 3 c.LFLX_20.000 60.002 10.001 10.006 2 c.LFLX_30.002 90.004 20.003 3-0.008 2 c.LFLX_40.000 20.003 10.001 20.008 5 c.LFLX_5 0.000 0 0.000 00.000 00.000 0

表7 模型优化结果Tab.7 Model optimization resultsLFLX固定效应作用位置模型表达式模型编号R2MAERMSEaCW=a×LFLX+b×D+c×D22.10.728 50.680 90.823 4bCW=a+b×LFLX×D+c×D22.20.734 40.695 20.826 7cCW=a+b×D+c×LFLX×D22.30.774 30.648 70.764 6a、bCW=a×LFLX+b×LFLX×D+c×D22.40.7390.696 40.811 5b、cCW=a+b×LFLX×D+c×LFLX×D22.50.7280.690 60.805 4a、cCW=a×LFLX+b×D+c×LFLX×D22.60.7280.680 90.791 6a、b、cCW=a×LFLX+b×LFLX×D+c×LFLX×D22.70.686 60.709 20.848 9
CW=0.196 9+0.165 8×D-0.001 7×
LFLX×D2
(6)
式中:LFLX表示林分类型固定效应。
2.3 模型评价
运用检验数据对改进模型2.3进行验证,结果如表 8所示。对于建模数据,相比于基础模型,改进模型的决定系数增加了60.24%,平均绝对误差降低了12.99%,均方根误差降低了17.86%。改进模型2.3相比于基础模型2,其检验数据决定系数增加了50.25%,平均绝对误差降低了9.5%,均方根误差降低了13.93%。所以,选择改进模型CW=0.1969+0.1658×D-0.0017×LFLX×D2作为最终模型,用于湖南省栎类次生林胸径—冠幅模型预测。同时也可以看出,林分类型对于冠幅影响较大。

表8 模型评价指标Tab.8 Model evaluation index模型建模数据检验数据R2MAERMSER2MAERMSE基础模型20.483 20.745 50.930 80.481 40.753 30.943 9改进模型2.30.774 30.648 70.764 60.723 30.681 40.0.812 4
3 结论和讨论
冠幅与胸径都是描述树木生长的重要指标。此外,还有其他因子影响树木的生长发育。与Calama等[20]的研究方法类似,首先从常见的冠幅模型中选取一个较好描述冠幅与胸高直径关系的模型作为基础模型,在此基础上引入新的林分变量,从而使模型精度得以提升、模型适用性更广。本研究从5个合适的冠幅—胸径候选模型中,选取拟合精度最高R2(0.483 2)、误差最小MAE(0.7455)、RMSE为0.930 8的Quatriatic模型作为基础模型。
随着统计学与计算机的发展,广义模型被更多的学者用于立地条件复杂、林分结构多样的林分。付利勇等[11]以黄丰桥国有林场的杉木为研究对象,考虑立地指数和样地对冠幅生长的随机影响,与基础模型相比,他们构建了嵌套两水平非线性混合冠幅模型,预测精度明显提升。此外,朱光玉等[21]建立了含林分类型或立地类型的栎类天然混交林断面积生长模型,发现含哑变量模型能有效解决天然混交林优势树种分布与立地类型的差异对林分断面积预估的影响,并大幅提高了模型的预测精度。本研究采用数量化方法I对林分类型、树种、优势木高、林分密度等4个林分因子进行了显著性筛选,发现林分类型对湖南省栎类次生林冠幅的生长有显著性影响。进而将其作为固定效应分别加在二次型Quatriatic基础模型的参数上进行优化,最终确定以改进模型CW=0.196 9+0.165 8×D-0.001 7×LFLX×D2作为最终的模型(R2=0.774 3、MAE=0.648 7、RMSE=0.764 6),用于湖南省栎类次生林胸径—冠幅预测模型。
通过在模型中增加其他因子作为固定效应,可以让各个样地之间的效应差异降到最小。在实际操作时,样地的随机性决定了样地之间可能会产生随机效应。所以,如果想了解不同样地随机效应对冠幅的影响,则需要把样地作为固定效应,分别添加在模型的各个参数上,构建非线性混合效应模型,这一方向还需要我们进行深层次的研究[22]。
