崩塌滚石对高压输电线路铁塔的危险性评估
2021-07-02李浩言岳灵平江泓陈家乾孙峰蒋峰
李浩言,岳灵平,江泓,陈家乾,孙峰,蒋峰
(1. 浙江湖州电力设计院 输电运检中心,浙江 湖州 313000;2.国网浙江省电力有限公司 湖州供电公司,浙江 湖州 313000;3.三峡大学 电气与新能源学院,湖北 宜昌 443002)
滚石往往都是伴随着滑坡失稳而来的。所谓滚石,是指个别块石因某种原因从地质体表面失稳后,经过下落、回弹、跳跃、滚动或滑动等运动方式中的一种或几种的组合,沿着坡面向下快速运动,最后在较平缓的地带或障碍物附近静止下来的一个动力演化过程[1]。滚石事件的发生一般都是突发的、随机的,所以人们很难预测并且控制滚石灾害的发生。我国是一个受滚石危害严重的国家,据不完全统计,我国每年在滚石中有数百人死亡。目前,我国对滚石有一定的研究,其中包括滚石运动特性的影响因素分析、滚石对桥墩的冲击响应分析、滚石对钢筋混凝土板的冲击力分析以及滚石对各种缓冲材料的冲击特性研究。学者通过大量的实验以及仿真分析,总结了滚石的一些运动规律,冲击力计算理论以及滚石对各种缓冲材料的撞击响应分析[2],为研究滚石提供了经验和理论方法,但是由于铁塔结构的特殊性和滚石运动路径的复杂性,滚石撞击铁塔不同的部位或者铁塔塔型的不同都会产生不同的结果。本文运用Rockfall软件建立一个模型坡面,对滑坡滚石进行运动轨迹、弹跳高度和动能变化的模拟,结合赫兹碰撞理论,通过能量守恒定理和日本公式对滚石的最大冲击力进行理论估算。通过比较不同弹跳高度的滚石最大冲击力的大小和不同质量滚石的冲击力大小,综合分析滑坡滚石灾害对山区铁塔造成的危害,定量分析滚石对铁塔的影响,为山区铁塔的防撞结构研究提供参考。
1 滚石运动轨迹的模拟与分析
1.1 基本假设
Rocfall是一款基于概率统计理论的危岩落石滚落路径模拟软件。由于影响落石运动特性的因素众多,且具有复杂性特征,因此本文在运用 Rocfall软件进行有关模拟时作出如下假定:1)危岩体边坡坡面由若干折线段组成,不考虑坡面的突出和凹陷,忽略坡面物体微小差异对落石的影响;2)落石为质量均质的球体,忽略形状对落石的影响;3)落石在滚落过程中不考虑破碎解体,保持完整,且落石与坡面均为各向同性体;4)不考虑空气阻力和升力对落石的影响。
1.2 模型参数设置
滚石的运动方式较复杂,通常都是由自由落体、弹跳碰撞、滚动、滑动等多种方式共同构成,除此之外,不同的垫面性质以及滚石与不同垫面碰撞时的恢复系数和摩擦系数也存在着较大的差异,这些因素都会导致滚石的运动特性大不相同,因此坡面模型参数的设置是非常关键的。本文建立一个模型坡面,结合不同垫面的恢复系数和滑动摩擦系数取值[3]对坡面材料参数进行设置,坡面模型如图1所示。

图1 滚石坡面模型
滚石坡面模型共分为六段,其对应的参数见表1。
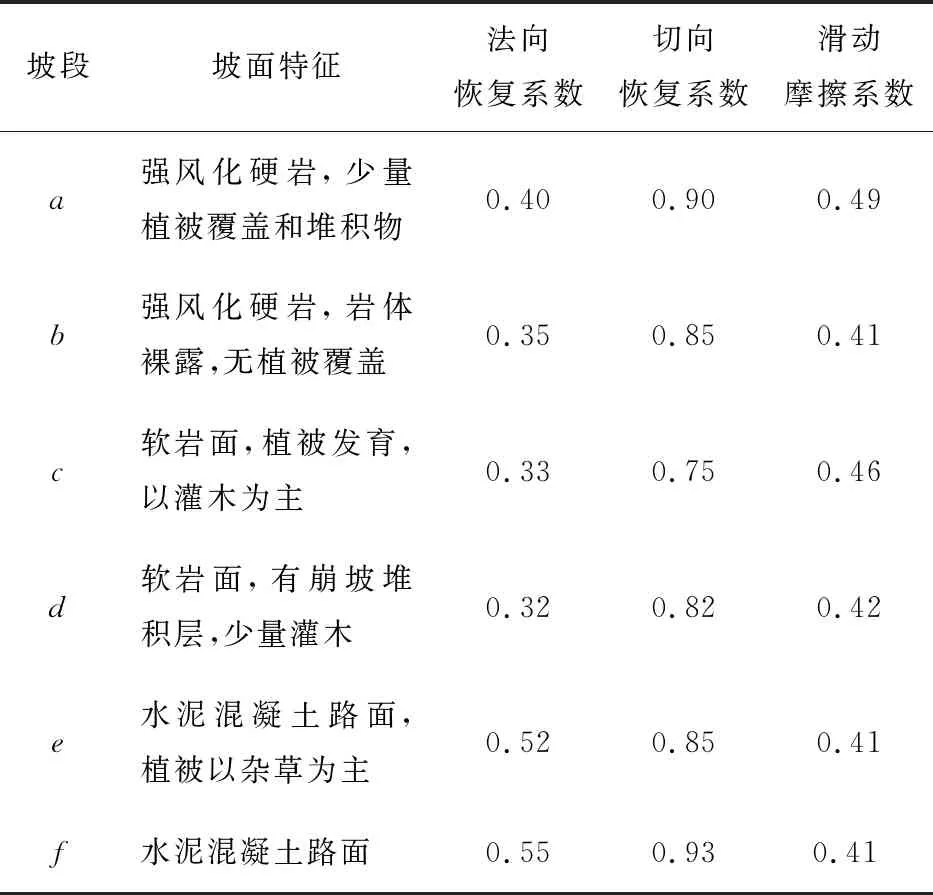
表1 坡面模型各段参数取值
通过Rocfall软件对滚石运动的轨迹、速度、弹跳高度以及总动能的变化进行模拟。为了使模拟实验结果更加真实可靠,模拟采用的滚石质量分别为50、100、200 kg,数量为每组50个。
1.3 模拟结果与数据分析
滚石的运动轨迹如图2所示。从图2的滚石运动轨迹曲线可以看出,50、100、200 kg的滚石运动轨迹大体相似,它们大部分都集中在了距离坡底75~140 m处,并且随着滚石质量的增加,滚石弹跳的高度和最终停下时的水平距离也有所增加,这意味着滚石对坡底的建筑物影响范围也越大。

(a)50 kg
滚石的弹跳高度变化如图3所示。由图3可知,滚石模拟仿真的结果中滚石弹跳高度有两个较为明显的峰值。其中一个是在b段左右,这是由于b段坡度较大,滑动速度陡然增加,滚石在重力加速度的作用下加速飞跃下来,最大的弹跳高度达到了28 m。另一个出现在d段之后,滚石在自重作用下首先冲击到d段,因为d段植被覆盖较好,所以滚石又再次发生滚动到达e段,e段为水泥混凝土路面,该段的恢复系数较大,滚石又出现了第二个弹跳峰值,高度为13 m,最后滚石在150 m之后变为滑动。50、100、200 kg滚石弹跳高度的区别主要体现在第二次弹跳峰值时,质量越大的滚石,弹跳高度越大,从而导致其滑动的距离越远,因此可以发现,质量越大的滚石越容易对坡底的建筑造成破坏。

图3 滚石弹跳高度变化曲线
滚石的速度变化如图4所示。由图4可知,滚石以0的初速度从硬岩段开始下滑,到达b段陡坡后直接飞跃而下,该过程中重力势能转化为动能,速度呈线性增加,在撞击到坡面后速度达到最大值38 m/s;随后因为撞击影响,一部分动能转化为内能,速度有所降低;之后的一段时间滚石的运动都是弹跳滚动的方式,内能不断消耗,势能也随之减小,所以速度不断降低,由于水泥面的摩擦力较小,滚石的运动近似匀速运动,最后的速度为6 m/s。由于假定落石和坡面都是各向同性的均质体,所以在每次撞击过程中速度都呈线性减小。研究认为,考虑瞬间摩擦消能的作用,落石的切向速度在碰撞过程中损失10%[4]。由图4还可以看出,滚石在经过第一次碰撞后,质量越大的滚石,速度变化的峰值也越大,第一次碰撞之后的最大峰值还可达到25 m/s左右,由此可见,在坡底路段设置一些防护装置来缓冲滚石的冲击速度是很有必要的。
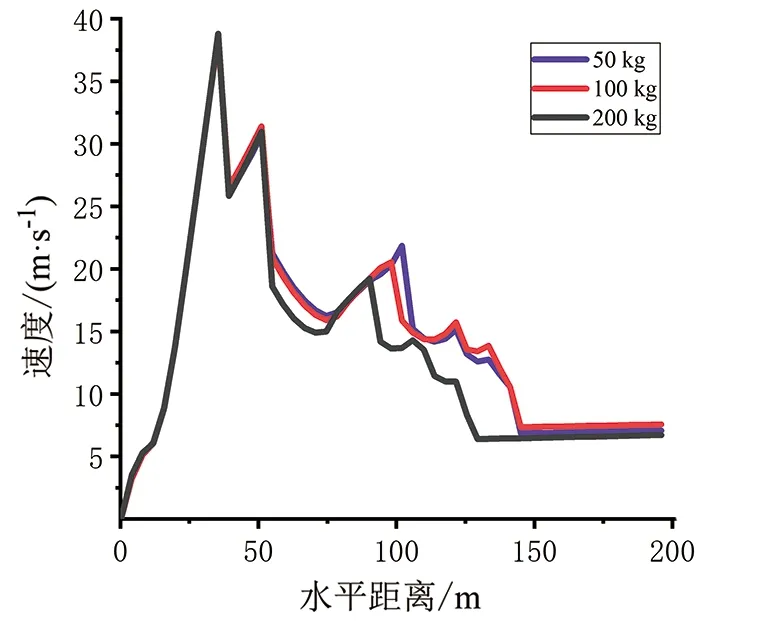
图4 滚石速度变化曲线
滚石的动能变化如图5所示。由图5可知,滚石的动能首先随着势能的减少呈线性增加,最大峰值达到150 kJ,然后与坡面碰撞后,一部分动能转化为内能,随后发生弹跳、滚动,动能在小幅波动的过程中逐渐减小,在这过程中滚石的最大峰值也高达60 kJ。通过对比发现,质量越大的滚石在弹跳过程中动能增加越大,并且在滚动摩擦的过程中,质量大的滚石由于摩擦损失的动能百分比也要比质量小的大。综合图2—图5可知,山区滚石的防治位置选在距离坡底25~75 m处较为合适。

图5 滚石动能变化曲线
2 滚石冲击力对铁塔的风险评估
现阶段国内外对滚石撞击路基、钢筋混凝土和桥墩等研究较多,但是对于滚石对铁塔的碰撞冲击研究还不够成熟。为了减少滚石对铁塔的破坏影响,需要对滚石撞击铁塔时的冲击力进行预估和评价。研究滚石冲击力常用的计算理论包括Hertz碰撞理论[5]和基于冲量定理理论[6],而在滚石冲击力的计算公式研究中,不少学者都有自己的见解,其中我国杨其新等[7]提出了计算落石冲击力的试验公式,为工程设计提供基本依据;澳大利亚Pichler等[8-9]模拟落石对砂砾土质垫层的冲击,得到一种半经验法的冲击力计算公式;日本Kawahara[10]基于落石冲击力试验数据,模拟落石自由下落情形下的落石冲击力;瑞士 Labiouse等[11]考虑弹性碰撞理论得到半经验法公式。但是上述方法都有自身的局限性,它们的使用都有一定的限制条件。所以本文将采用两种冲击力计算方法综合分析滚石对铁塔的冲击力影响,其一是日本公式[10],用来分析自由落体的滚石对铁塔的冲击力影响,该方法的局限性在于滚石的运动方式是自由落体,这可以对应地分析类似图1中d坡段铁塔受滚石冲击力的影响;其二运用冲量定理的理论计算模型以及基于能量守恒理论的计算方法[12]分析坡底的铁塔受滚石冲击力的影响。为了简化计算,本文把滚石撞击角钢材料而得的冲击力看成是滚石撞击铁塔的冲击力。
2.1 日本公式计算最大冲击力
日本公式是根据Hertz碰撞理论,在滚石冲击力试验数据的基础上给出的计算公式,它的局限性在于只能讨论自由落体的滚石,因此运用公式来计算滚石从坡顶下落到第一次撞击坡面时的冲击力,铁塔材料参数采用Q235角钢的参数,该公式为

(1)
式中:g为重力加速度;m为滚石质量;H为滚石从坡顶到第一次撞击坡面的高度;λ为拉姆常数(kPa),其计算公式为
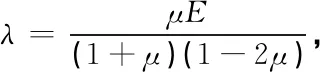
(2)
式中E、μ分别为角钢材料的弹性模量和泊松比。
2.2 能量守恒理论计算最大冲击力
为了简化问题,把滚石与角钢的碰撞看成弹性碰撞,发生冲击后,滚石能量损失全部转化为铁塔角钢的弹性形变能量,其中滚石损失的能量为
(3)
式中:m1为滚石的质量;v0为碰撞前滚石的速度;v1为碰撞时滚石的瞬时速度。角钢的弹性形变能量为

(4)
式中:k为角钢的刚度;δ为角钢的极限压缩量。而k又有
(5)
式中:A为滚石与角钢的接触面积;G为角钢的剪切模量;μ为角钢的泊松比。根据能量守恒定律可以得到
ΔE=W。
(6)
当滚石碰撞的瞬时速度变为0时,角钢的压缩量达到最大值δmax,此时的滚石冲击力达到最大值,即
Fmax=kδmax。
(7)
2.3 铁塔安全性评估
以上两种理论的计算值都非常接近实际情况,因为在理论计算时,滚石撞击的是角钢材料而不是整个铁塔,理论计算中的冲击力大小可能存在偏大的情况,但是在实际中,铁塔的结构就是由角钢构成的,滚石往往会冲击在角钢上,并且接触面积非常的小,这就使得理论值更加贴近事实,并且避免了复杂的计算过程。本文通过上述两种理论公式对滚石冲击力进行计算,取两者的较大值,计算出50 kg滚石最大冲击力为1.8×104N,200 kg的为1.33×105N。假设滚石与铁塔撞击处角钢的总接触面积为0.005 m2,那么铁塔在该处受到50 kg滚石产生的应力大小为3.6×106Pa,200 kg滚石产生的为2.55×107Pa。根据铁塔杆件所能承受的允许应力表[13]可以得到,塔腿和塔身各杆件能承受的应力在10~50 MPa之间,而200 kg滚石产生的应力大小为25.5 MPa,显然已经对铁塔造成了严重的威胁。通过Rocfall仿真图中的动能变化曲线可以看出,铁塔还在极短的时间内承受6×104~1.5×105J的能量,这对铁塔无疑是致命的伤害。
3 结论
1) 结合不同垫面的恢复系数和滑动摩擦系数取值对坡面材料参数进行设置,利用Rocfall软件得到了滚石在该坡面上的运动参数,包括滚石速度,总动能以及弹跳高度。
2)通过对仿真模拟结果分析,发现滚石速度的峰值,总动能以及弹跳高度的峰值与滚石质量整体上都是成正比的,因此滚石防治的重点还是质量较大的滚石。
3) 切向恢复系数、法向恢复系数和陡坡段坡高均与滚石的运动距离正相关, 即滚石的运动距离随着3种因素的增大而增大
4) 通过Rocfall软件对不同质量滚石的运动过程进行模拟,从而预测滚石的运动轨迹,发现滚石第一个落点在靠近坡底的两个坡段转折处,并且能量非常大,最后停留在距离坡底25~75 m区域内,因此,必须在第一个落点和该处危岩下方实行被动防治,如缓冲墙、拦石网和泡沫垫层等防护工具,它们的设置参数及防治可参考本文结果。
