基于动力学和预瞄理论的超车路径跟踪控制
2021-07-02孙梅霞满绪民王吉华郭栋满绪豪
孙梅霞,满绪民,王吉华,郭栋,满绪豪
(1. 山东理工大学 学报(自然科学版)编辑部, 山东 淄博 255049;2. 济南轨道交通集团第一运营有限公司 车辆部, 山东 济南 250301;3. 山东理工大学 交通与车辆工程学院, 山东 淄博 255049;4. 烟台大学 文经学院,山东 烟台 264005)
辅助超车包括超车路径规划和对规划好的路径实行跟踪控制,其中后者对超车安全性和超车的顺利进行具有重要意义,国内外专家学者对其进行了很多研究并取得相应成果。张朋飞等[1]设计了THMR-V智能汽车,提出了基于混合模糊逻辑的控制方法实现机器人路径自动跟踪。张丽霞等[2]提出了最优控制路径跟踪。游峰等[3]应用了动态位姿误差,选取Lyapunov函数利用Backstepping设计路径跟踪控制器。徐丽娜[4]阐述了利用神经网络控制器实现机械臂的转角跟踪参考模型输出转角的控制。Boada等[5]以汽车操纵稳定性作为研究重点,设计了模糊控制算法的路径跟踪控制器。Soudbakhsh等[6]设计了线性二次型最优LQR算法的路径跟踪控制器,利用Carsim验证了控制可行性。Isermann等[7]提出了状态反馈加前馈方法来实现路径跟踪。Hegedüs[8]利用闭环轨迹跟踪控制模拟了车辆的行为。
国内外已有很多控制算法用于路径跟踪或辅助超车换道,但预瞄理论符合驾驶员的驾驶特性,所以将其应用于路径跟踪控制,正引起国内外研究者的重视。目前,将预瞄理论应用于超车的路径跟踪控制研究较少, 因此本文基于车辆动力学和单点及多点预瞄方法对其进行研究,并对五次多项式规划的路径和Carsim自带的双移线路径进行控制仿真。
1 超车车辆侧向动力学模型
车辆的线性二自由度模型能够很好地反映车辆在水平地面转向行驶的侧向动力学特性,适合于超车过程的路径跟踪控制,采用前轮转向的二自由度侧向动力学模型如图1所示。
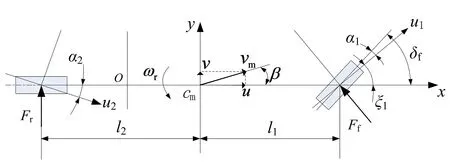
图1 车辆二自由度侧向动力学模型
图1中,cm为车辆质心;o为转向中心到车辆纵轴线垂线和纵轴线交点;l1、l2分别为车辆质心到前轴和后轴的距离;u为车辆纵向速度;v为质心侧向速度;vm为车辆质心速度;汽车质心侧偏角β=v/u;ωr为横摆角速度;δf为前轴转角;u1、u2分别为前后轮实际运动速度;α1、α2分别为前后轮侧偏角;Ff、Fr分别为作用于前后轮的侧向力。由轮胎和车辆运动学定理可得
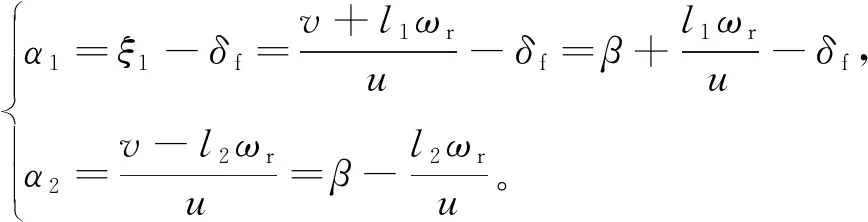
(1)
图1中,在y轴方向应用动力学第二定律、在车辆质心上应用动量矩定理,可得
(2)
式中:m为车辆总质量;Iz为车辆转动惯量;ay为侧向加速度。
高速超车前轮转向角度小,轮胎侧偏特性为线性,设前后轮侧偏刚度分别为k1和k2,则Ff=k1α1,Fr=k2α2,将ay=dv/dt+uωr[9]和(1)式代入(2)式,并忽略高速前轮转向的小角度δf和前后轮小侧偏角α1和α2,并化简得
(3)
2 基于预瞄理论的超车路径跟踪
超车过程中,基于预瞄理论对规划路径进行跟踪,其原理如图2所示,在预瞄跟踪范围内实际路径和规划路径近似为重合。图2中,or为转向中心;p为预瞄点;dp为预瞄距离;E为预瞄误差;R为车辆转向半径。由几何关系可得
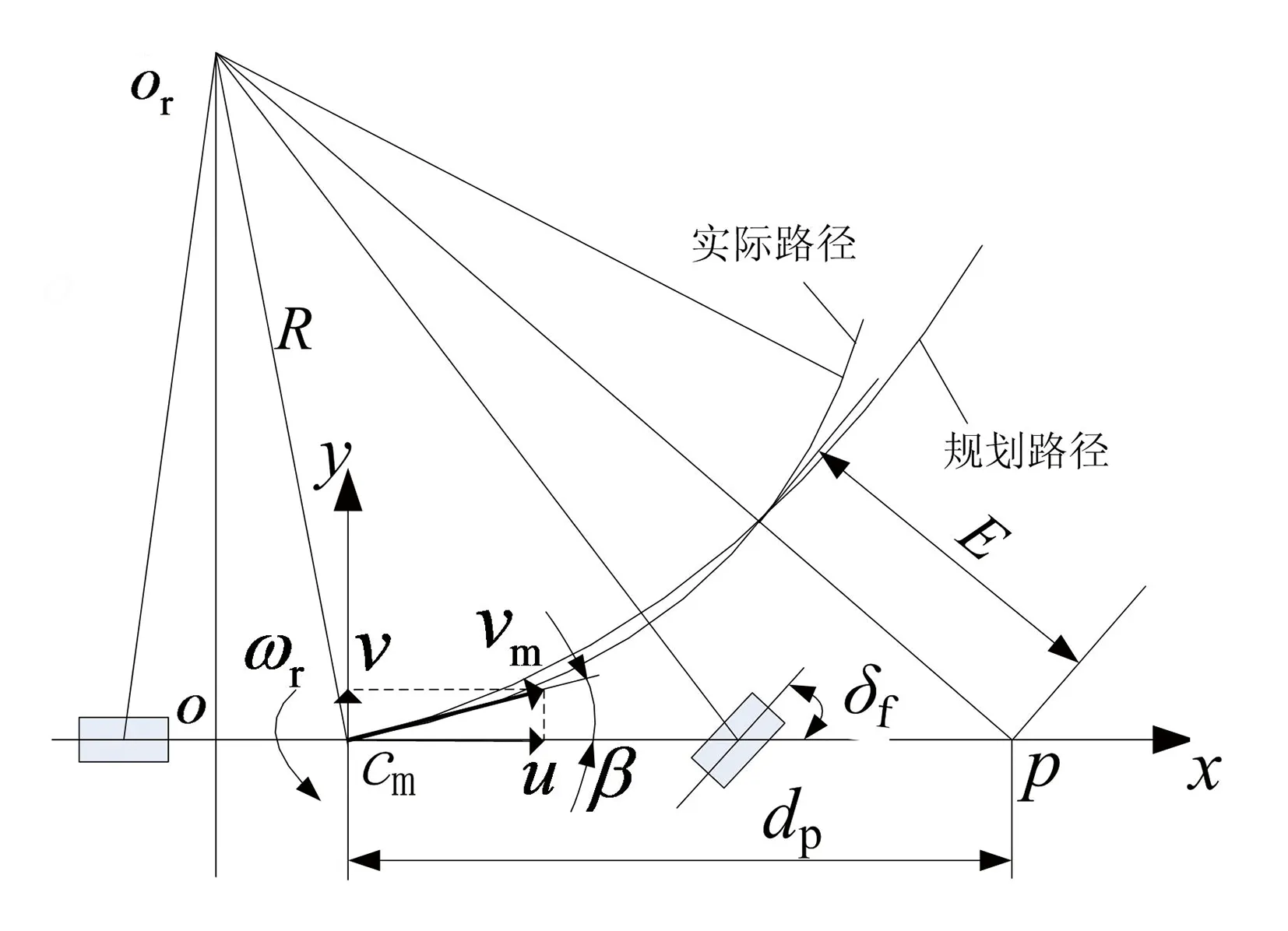
图2 基于预瞄理论的路径跟踪原理
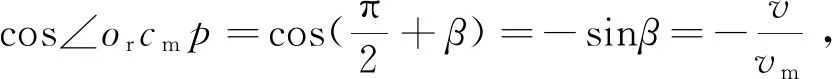
(4)
由三角形余弦定理可知,预瞄误差E为
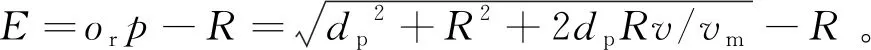
(5)
由图1和图2均可得到vm、ωr和v的关系为
vm2=R2ωr2=u2+v2。
(6)
车辆在超车转向时,沿期望路径作稳态行驶,则侧偏角β和横摆角速度ωr趋于稳定值,即dβ/dt和dωr/dt均为零,于是由(3)式可得

(7)
由(7)式求出ωr和δf、β和δf关系如下:
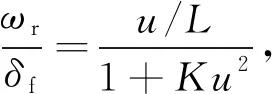
(8)
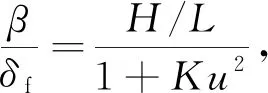
(9)
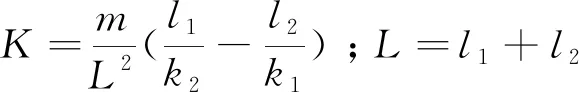
由(9)式除以(8)式得到v和ωr关系如下:
(10)
将(10)式和(6)式代入(5)式,可得
(11)
将(8)式和(9)式代入(6)式,可得
(12)
由(11)式和(12)式可得到前轮转向角δf和预瞄误差E的关系为
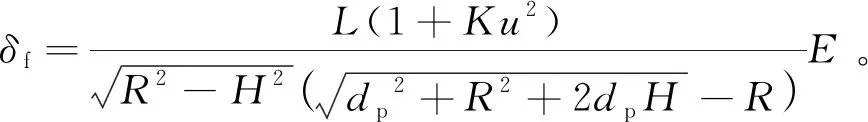
(13)
基于泰勒公式,可将(13)式中的转向半径R消去[10],得到δf和E的近似简化表达式为
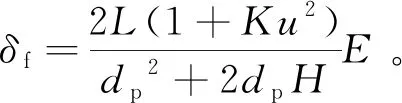
(14)
(14)式是基于单点预瞄而得到的路径跟踪所需前轮转角,由车辆参数、预瞄距离dp和对应的预瞄误差E确定。但单点预瞄所获得的跟踪路径信息非常有限,驾驶员实际驾驶过程中,为了得到前方道路更多的信息,将会采用多点预瞄[10],如图3所示。图3中,pi表示第i个预瞄点,Ei表示第i点的预瞄误差且i=1,2,…,n。
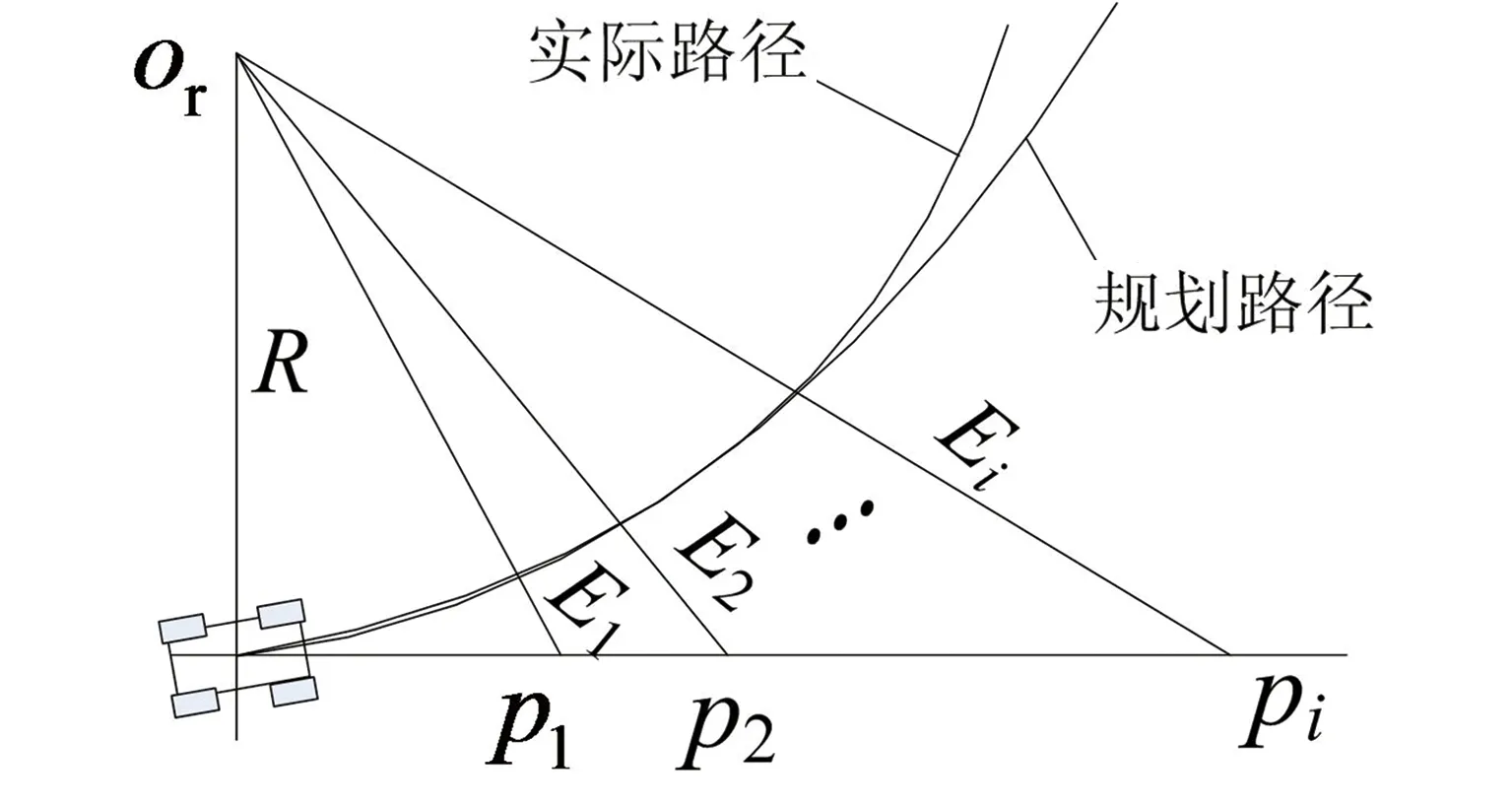
图3 多点预瞄
在多点预瞄过程中,各点的预瞄重要性对路径跟踪的作用是不同的,因此将对各点的预瞄误差取权重,可得

(15)
式中:E为总的预瞄误差;wi为预瞄误差的权重系数,i=1,2,…,n。则根据(14)式可得到路径跟踪的前轮转角为

(16)
3 最优预瞄路径跟踪的建模与仿真
3.1 超车路径跟踪控制模型
在Simulink中建立根据预瞄误差求前轮转角的计算模型,在Carsim中设置规划的路径和车辆参数,定义二者的输入输出接口并进行联合仿真。选用的样车部分参数见表1。
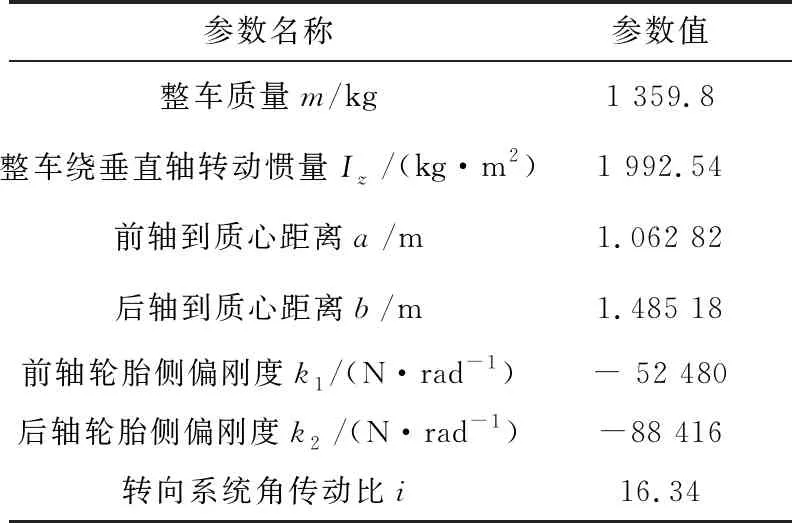
表1 样车部分参数
(16)式为路径跟踪的控制器模型,其输入为预瞄误差,输出为前轮转角控制量,Simulink中转角计算子系统如图4所示,联合仿真模型如图5所示。设控制对象为车辆,其输入量为前轮转角,输出量为预瞄误差和跟踪误差。仿真时,运行Carsim模型将调用Simulink控制器模型。
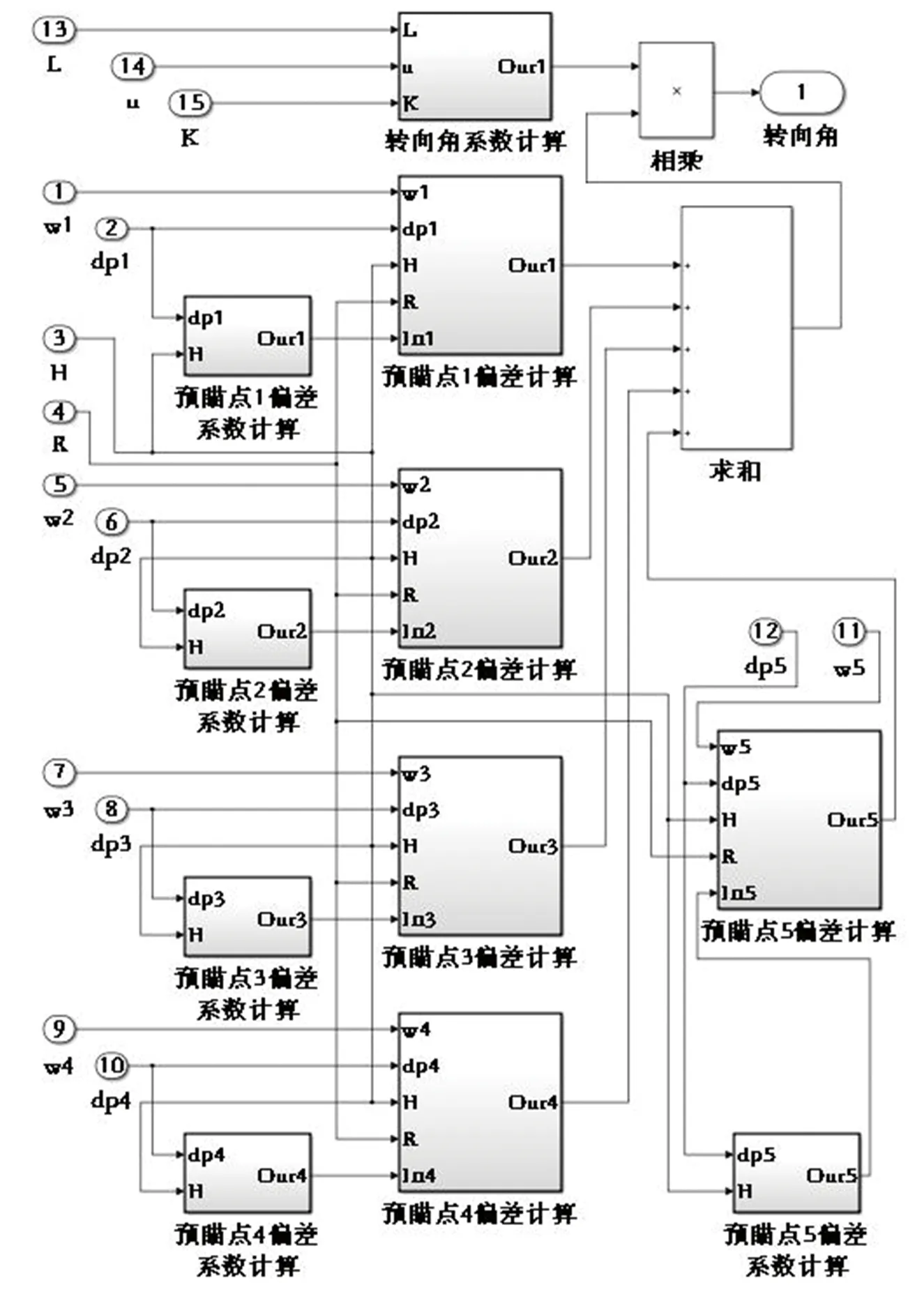
图4 转向角计算子系统
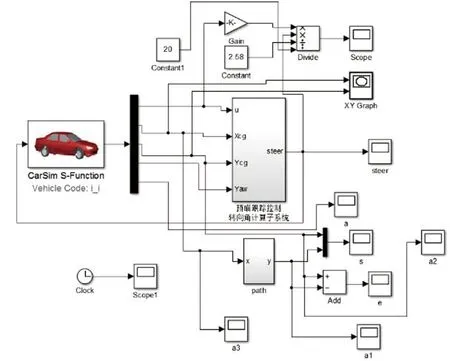
图5 CarSim与Simulink联合仿真的超车路径跟踪模型
3.2 多项式规划路径仿真
为验证不同车速和不同预瞄距离下路径跟踪算法的效果和影响,设置超车换道规划路径为五次多项式,分别在相同预瞄距离、不同车速和相同车速、不同预瞄距离两种情况下进行仿真。
3.2.1 相同预瞄距离、不同车速
设置五点预瞄,预瞄距离分别为8m、9 m、10 m、11 m和12 m,车速分别为80 km/h、100 km/h和120 km/h,仿真结果如图6和图7所示。图6为规划路径的侧向跟踪位移,3种速度分别对应不同的规划路径,3种车速的侧向跟踪路径分别与各自的规划路径相靠近。图7为跟踪误差,车速80 km/h、100 km/h和120 km/h的最大跟踪误差分别为0.13 m、0.17 m和0.2 m,平均误差分别为0.065 m、0.071 m和0.083 m。结果表明,在高速限速120 km/h以内的超车换道过程中,跟踪的侧向位移误差随车速增加而增加,但最大误差不超过0.2 m,平均误差不超过0.09 m,说明基于预瞄理论的路径跟踪方法可在高速时较好地跟踪规划路径。
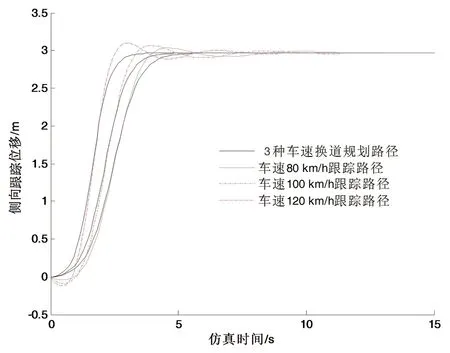
图6 不同车速超车换道的路径跟踪仿真
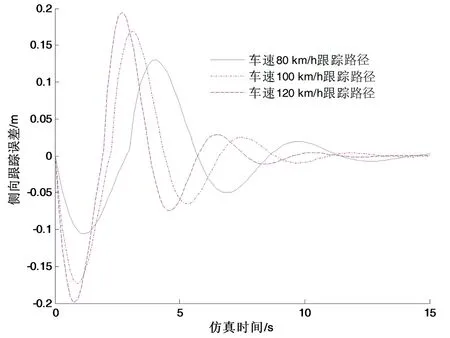
图7 不同车速超车换道的侧向位移跟踪偏差
3.2.2 相同车速、不同预瞄距离
设置车速为80 km/h,3组预瞄的距离不同。预瞄1:1 m、2 m、3 m、4 m和5 m,预瞄2:8m、9 m、10 m、11 m和12 m,预瞄3:15m、16 m、17 m、18 m和19 m,仿真结果如图8和图9所示。 图8为侧向跟踪位移,图9为跟踪误差。由图9可知,预瞄1、预瞄2和预瞄3的最大跟踪误差分别是0.15 m、0.13 m和0.175 m,预瞄2的跟踪误差最小,从而说明,预瞄距离过大或过小均会使跟踪误差增加,在平均预瞄距离大约为10 m时,将得到较小的跟踪误差,跟踪效果较好。
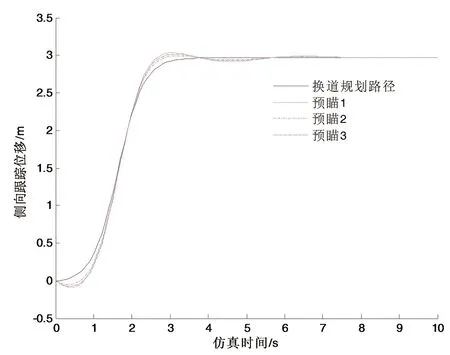
图8 不同预瞄距离超车换道的路径跟踪仿真
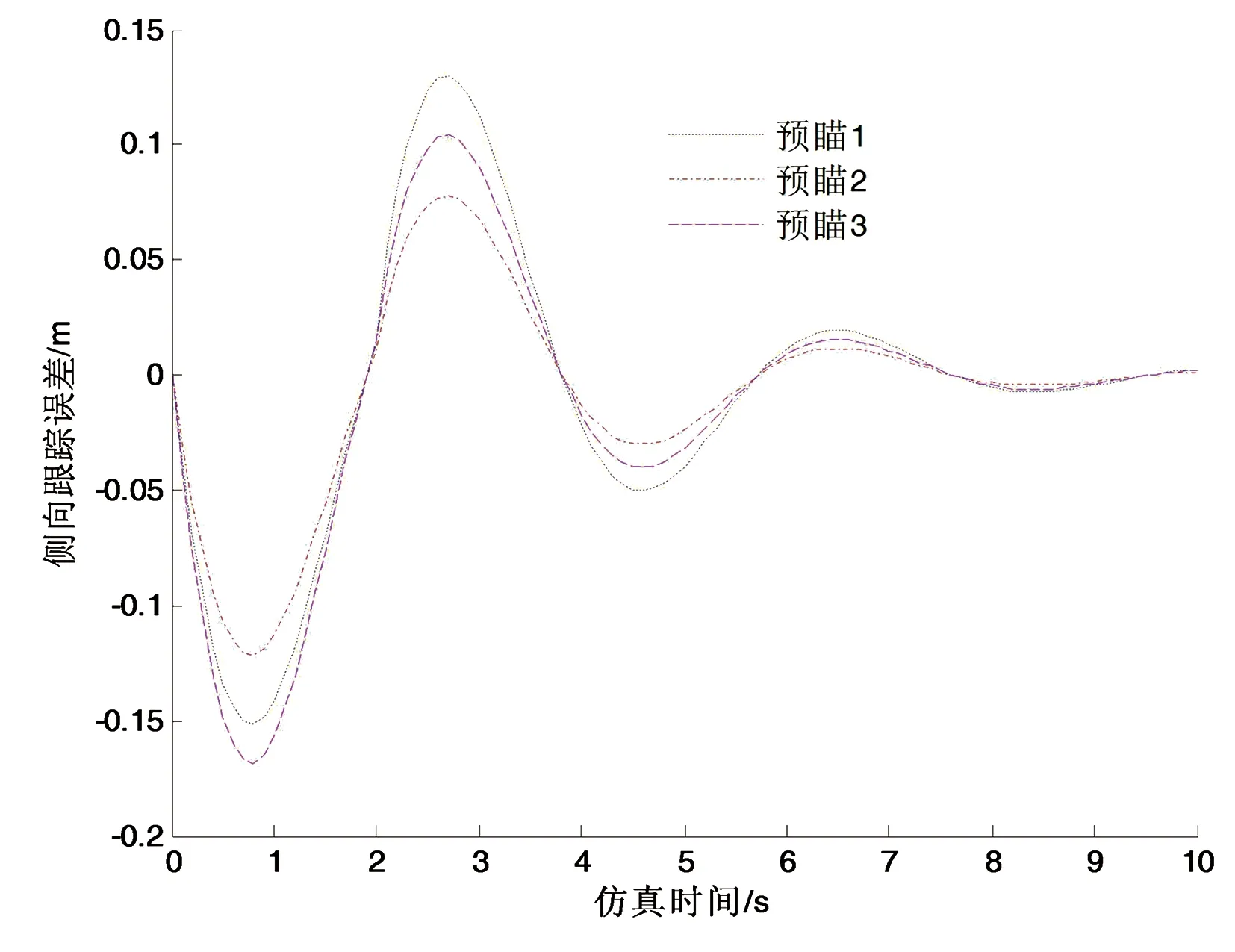
图9 不同预瞄距离超车换道的侧向位移跟踪偏差
综合说明,选用了合适的预瞄距离,在高速限速120 km/h以内的超车换道,控制器均可使不同车速的预瞄控制得到较好的路径跟踪效果。
3.3 双移线路径仿真
设置超车规划路径为Carsim内置的双移线,车速仍设置为80 km/h,仿真结果如图10所示。
由图10可知,跟踪双移线规划路径时,在较长的平直路段,实际侧向位移最大误差约为0.12 m;在半径很小弯道处的最大跟踪误差约为0.33 m,平均误差为0.083 m,比大半径弯道和平直路段的跟踪误差稍大。仿真中的双移线存在很小半径的弯道,只是为了验证跟踪控制的这种可行性;但为了高速超车的安全性,实际中高速超车的规划路径不能是小半径弯道,即车辆不会大角度转向,所以结果也同样说明了高速时预瞄路径跟踪方法的有效性。
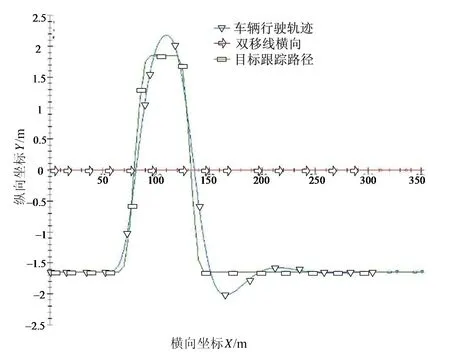
图10 超车换道过程路径跟踪仿真结果
4 结束语
将车辆动力学理论融合到预瞄理论设计了路径跟踪控制器,并进行了仿真和分析,得到了较好的跟踪效果。设计的控制系统是开环形式,如果采用闭环形式可能会得到更好的跟踪控制效果,这也正是今后将要研究的工作。
