基于避撞轨迹跟踪的车辆稳定性控制仿真研究

周龙辉，石沛林，蒋军锡，张亮，梁明磊，侯建伟

(山东理工大学 交通与车辆工程学院, 山东 淄博 255049)

车辆行驶安全问题一直是人们关注的热点，由之产生的汽车主动安全是近年来国内外研究的热点之一。在车辆安全避撞方面，由于制动距离随车速呈指数增长，因此在车速较高时制动避撞局限性较大。统计结果表明，至少有24%的追尾事故可以通过转向规避[1]，故可采用转向换道避撞的方式对制动避撞进行弥补。

模型预测控制是一种滚动求解带约束优化问题的控制方法，其最大的优势是能在控制过程中增加多种约束，从而更合理有效地控制车辆的路径规划和跟踪过程[2]。然而，对于较低附着路面下的转向避撞轨迹跟踪，模型预测轨迹跟踪控制仍然容易出现车辆稳定性较差、控制调整时间较长及控制量调整过大等问题。为此，在车辆避撞轨迹跟踪过程中，提出对车辆施加横摆力矩控制以提高车辆稳定性，从而减少轨迹跟踪控制调整时间，更快、更准确地跟踪规划轨迹。

近年来，学者们针对汽车横摆力矩控制方法展开大量研究，主要的控制方法有PID控制、模糊控制、滑模变结构控制等。刘阳等[3]基于滑膜控制理论和模糊控制理论，设计四轮独立驱动电动汽车转向稳定性的横摆力矩控制策略，仿真分析表明，能够保证汽车转向行驶的稳定性。林程等[4]设计了以横摆角速度、质心侧偏角以及横摆角速度与质心侧偏角联合作为控制变量的3种等速趋近滑模变结构控制器，并利用仿真平台进行了验证，但滑模控制抖震现象较为严重。

本文采用模型预测轨迹跟踪与线性二次型调解器(LQR)对车辆横摆力矩联合控制的方法，实现车辆避撞轨迹跟踪过程中车辆的稳定性控制，改善轨迹跟踪控制效果。

1 模型预测轨迹跟踪控制

1.1 车辆动力学模型

运用模型预测轨迹跟踪控制首先需要建立相应的车辆理想化模型。本文采用具有侧向、横摆和纵向运动3个自由度的车辆模型，如图1所示。

图1中，坐标系o-xyz为车身坐标系，原点o为车辆质心所在点，x轴方向为车辆前进方向，y轴与车辆前进方向垂直，z轴垂直于xoy平面；坐标系O-XYZ为地面坐标系。

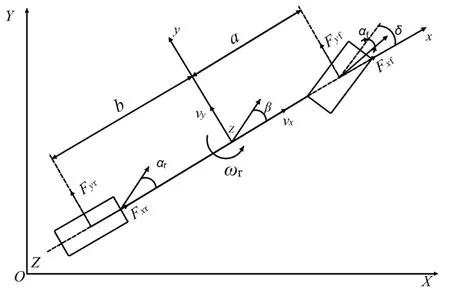
图1 三自由度车辆模型

模型预测轨迹跟踪控制的主要目的是使车辆快速而稳定地跟踪期望路径，属于车辆操纵稳定性问题，因此对悬架特性不作深入探究[5]。将车辆动力学模型进行如下理想化假设：车辆没有俯仰和侧倾运动；不考虑悬架垂直运动；忽略空气动力学影响；忽略因轮胎载荷变化而引起的轮胎特性变化及回正力矩变化[6]。根据牛顿第二定律建立车辆运动微分方程，即

(1)

式中：a，b分别为车辆质心到前、后轴的距离；m为车辆整备质量；Iz为车辆绕z轴的转动惯量；ωr为汽车横摆角速度；Fxf，Fxr分别为前后轮胎在x轴方向上所受的合力；Fyf，Fyr分别为前后轮胎在y轴方向上所受的合力；vx，vy分别为车辆在x轴、y轴上的速度。

车辆高速行驶时，一般情况下，前轮转角都较小。为简化模型预测控制器的设计，在车轮侧偏角、车辆侧向加速度较小的前提下，可将轮胎侧偏角与侧偏力看成线性关系。故在轮胎力的计算过程中提出小角度假设，即满足如下近似条件：

cosα≈1,sinα≈α,tanα≈α。

此时前后轮胎的侧偏角αf，αr计算关系式为

(2)

式中δf为前轮转角。

轮胎的滑移率计算关系式为

(3)

式中：ωw为车轮角速度；Re为车轮的滚动半径。

则前、后轮胎的侧向力为

Fyf=Ccfαf,Fyr=Ccrαr，

(4)

前、后轮胎的纵向力为

Fxf=Clfsf,Fxr=Clrsr，

(5)

式中：Ccf，Clf分别为前轮的侧偏、纵向刚度；Ccr，Clr分别为后轮的侧偏、纵向刚度；sf，sr分别为前轮、后轮的滑移率。

由于轨迹跟踪过程中需对车辆位置进行预测计算，故将车身坐标系转换为惯性坐标系，则车辆在惯性坐标系下的速度公式为

(6)

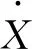
将轮胎力计算式(4)、(5)代入式(1)，得到线性轮胎假设条件下的三自由度车辆动力学模型。附加车辆坐标转换关系式(6)，整合得到

(7)

1.2 模型预测控制器设计

由于当前得到的是非线性系统，不能直接用于线性时变模型预测控制，故通过线性化方法[5]将式(7)线性化，得到线性时变方程

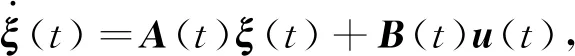
(8)

采用一阶差商方法将系统方程离散化，得到新的系统状态表达式

ξ(k+1)=A(k)ξ(k)+B(k)μ(k)，

(9)

式中：A(k)=I+TA(t)；B(k)=TB(t)；T为采样周期；I为单位矩阵。

由于车辆前轮转角改变量过大容易造成危险，且实际前轮转角控制执行装置存在物理极限，需增加约束将前轮转角δf和前轮转角增量Δδf限制在合理区间内,故将前轮转角控制增量作为最终输出的控制量，从而便于设定相关约束。

设定

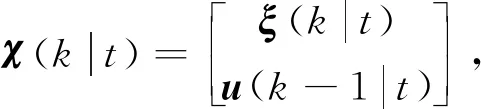
(10)

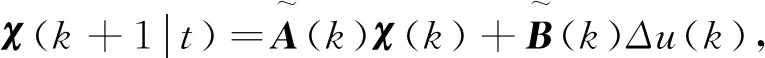
(11)

设预测时域为Np，控制时域为Nc，预测方程进一步写成

Y=Φkχ(k|t)+θkΔU(k)，

(12)

η=CY，

(13)

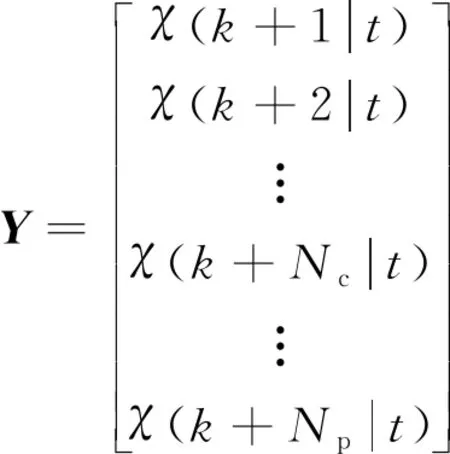
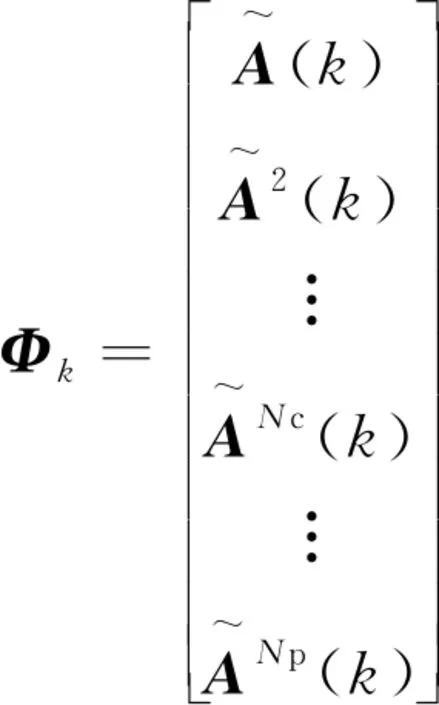
以前轮转角增量作为目标函数的控制量，目标函数表示为

(14)

式中：Q和R为权重矩阵；ρ为权重系数；ε为松弛因子。

设前轮转角范围和增量范围约束条件为

|δf|≤10°；|Δδf|≤1°。

最后运用Matlab的二次规划优化函数quadprog实时规划求解，得当前时刻前轮转角增量，并与上一时刻前轮转角求和，进而输出当前时刻前轮转角。

2 横摆力矩控制

2.1 控制模型的建立

汽车在良好附着路面上以较小的侧向加速度(一般认为小于0.4g)转向时，汽车的操纵特性可近似用线性二自由度车辆模型来描述，这时汽车操纵特性比较理想，驾驶员比较容易操纵汽车，汽车也是稳定的[7]。因此，本文将稳态时的线性二自由度车辆模型输出的横摆角速度参数作为汽车稳定性控制的目标，通过控制器产生附加横摆力矩，使车辆状态参数逼近控制目标参数，实现车辆稳定性控制。

稳态时车辆线性二自由度模型[8]表达式为

(15)

由此得到基于二自由度车辆模型的横摆角速度参考稳态值为

(16)

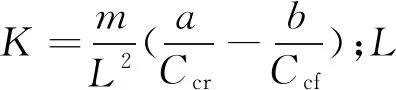
车辆安全行驶时，侧向加速度ay不能超过轮胎与地面能够产生的最大侧向加速度，于是设定理想横摆角速度的最大值约束，即

(17)

式中：g为重力加速度；μ为路面附着系数。

为尽量限制车辆侧滑，质心侧偏角参考稳态值设为0[9]。即

βref=0。

(18)

将汽车理想的质心侧偏角βref、理想的横摆角速度ωref、前轮转角δf代入线性二自由度车辆模型中，得状态方程如下：

(19)

汽车在失稳或接近失稳时已无法近似为线性系统，但为了寻找汽车横摆稳定力矩和汽车状态误差之间的简化关系，假定车辆的操纵特性依然采用A和B矩阵[8]，得到下式:

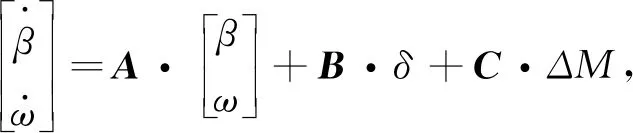
(20)

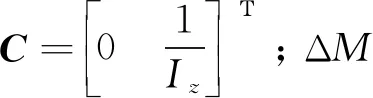
将式(20)减去式(19)得

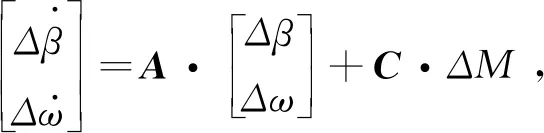
(21)

式中：Δβ=β-βref；Δω=ω-ωref。

式(21)可近似描述车辆实际参数和理想参数偏差与车辆稳定性控制所需附加横摆力矩之间的关系。由此关系式即可运用LQR方法求解最优的附加横摆力矩。

2.2 线性二次型最优求解

建立反映对状态误差和控制量要求的目标函数，即

(22)

式中：xlqr=[Δβ,Δω]Τ；ulqr=[ΔM]。

根据LQR方法，最优控制量表示为

u=-Klqr·x(t)

(23)

式中Klqr为状态反馈系数矩阵，且Klqr=[k1,k2]。

使用Matlab软件中的lqr函数求解得到

(24)

从而得到附加横摆力矩为

ΔM=-k1Δβ(t)-k2Δω(t)。

(25)

2.3 轮胎力优化分配

基于LQR方法求解出所需的附加横摆力矩，最终需要通过控制车轮制动力进而控制轮胎与地面之间的作用力来实现。本文采用基于最优轮胎力分配方法，考虑轮胎附着约束条件，引入优化目标函数，实现对制动力的分配。

2.3.1 轮胎力计算

求解轮胎力分配目标函数及建立相关约束需要通过轮胎模型对轮胎力进行计算估计。dugoff轮胎模型具有需求参数少、可以较好地表达轮胎非线性特征等优点，故本文采用dugoff轮胎模型对轮胎力进行估算。

车辆各轮垂直载荷如下：

(26)

式中：Bw为车辆轮距；h为车辆质心高度；ax为车辆纵向加速度；ay为车辆侧向加速度；Fz1为左前轮垂向载荷；Fz2为右前轮垂向载荷；Fz3为左后轮垂向载荷；Fz4为右后轮垂向载荷。

dugoff轮胎模型的轮胎侧向力数学表达式为

(27)

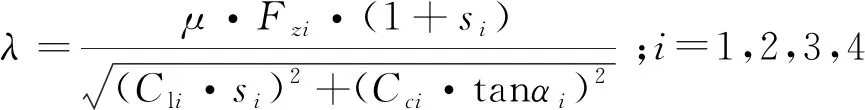
2.3.2 目标函数与约束条件建立

本文基于每个车轮的垂向载荷和能够提供的最大附着力建立目标函数，即

(28)

式中：Fxi为各轮目标纵向制动力；Fyi为式(27)得出的各轮侧向力轮胎模型计算值；Fzi为式(26)得出的各轮垂向力估计值。

由于在较低附着路面，通过轮胎制动能够产生的横摆力矩饱和后，不能达到上层控制器所期望的附加横摆力矩，故控制器分配到各轮胎上的制动力绕车辆z轴产生的力矩应不大于当前路面能够产生的最大附加横摆力矩，从而得到下式：

(29)

式中：Bw为车辆轮距；ΔMmax为当前路面能够产生的最大附加横摆力矩。

本文采用忽略纵向与侧向附着力差异的轮胎附着圆[8]作为轮胎力极限约束，故轮胎的纵向力和侧偏力应满足

(30)

对于制动控制，约束是单边的[10]，所以制动控制下轮胎纵向力约束条件为

(31)

2.3.3 轮胎力最优分配算法仿真实现

确定目标函数和约束条件后，轮胎力分配即可转变为非线性规划问题进行求解。使用Matlab软件中的fmincon函数在s-function中实时运行求解，即可得到对应的轮胎制动力Fxi，进而将制动力转化得到最终实现控制所需的制动轮缸压力，从而实现控制。

3 仿真分析

本文通过Matlab/Simulink与Carsim软件，对所设计的避撞轨迹跟踪及车辆稳定性控制进行仿真分析。仿真实验中的车辆模型参数见表1。

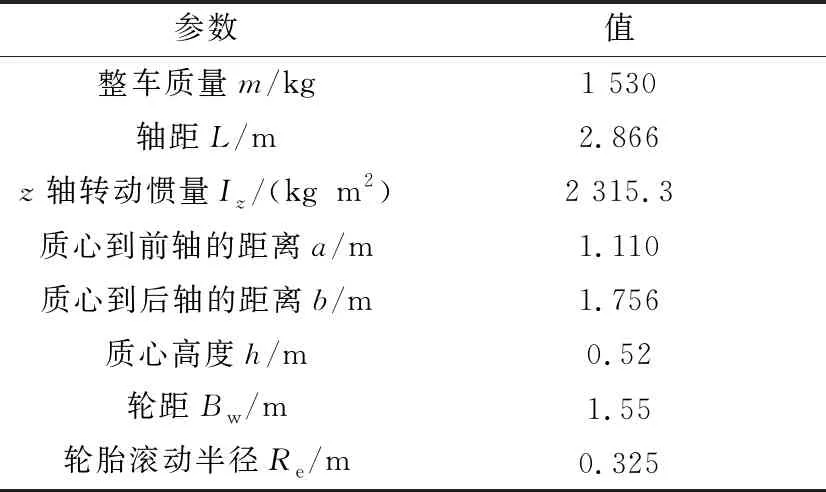
表1 车辆模型参数

目前，基于车辆避撞的换道轨迹有多种，对比分析后采用满足规划路径起止点约束和路径曲率约束的五次多项式换道轨迹。在O-XYZ地面坐标系中避撞轨迹方程如下：

(32)

式中：W为侧向位移量；d为避撞轨迹长度。

设车辆以75 km/h的车速在附着系数为0.4的路面上行驶。由于车辆在该仿真工况下采用短距离避撞轨迹易发生危险，又需通过跟踪避撞轨迹改善车辆纵向制动避撞局限性，故保守采用长度为40 m的避撞轨迹，同时选取一般道路宽度3.75 m作为轨迹侧向位移量。

为对比不同控制方法的作用效果，本文将仿真实验分为两种，分别为仅使用轨迹跟踪控制和使用轨迹跟踪、横摆力矩联合控制两种情况，并选取车辆行驶轨迹、横摆角速度、质心侧偏角、前轮转角作为评价指标，对不同控制方法车辆避撞过程的稳定性及轨迹跟踪效果进行分析。

图2为两种控制施加情况对应的车辆行驶轨迹对比。由图2可知，单一轨迹跟踪控制的车辆在避撞过程中出现了两次远离理想轨迹的较不稳定行驶轨迹；联合控制的车辆轨迹虽出现了少量超调，但行驶轨迹更加稳定，没有出现行驶轨迹再次远离理想轨迹的情况。

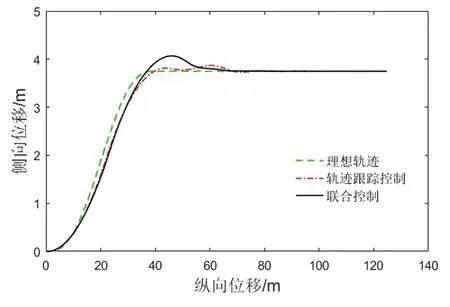
图2 行驶轨迹仿真曲线

图3为两种控制施加情况下仿真得出的车辆横摆角速度曲线。从图3中可以看出，仅使用模型预测轨迹跟踪控制的车辆，在避撞轨迹跟踪过程中的横摆角速度变化较大，震荡时间长；施加联合控制后，横摆角速度变化明显被抑制，到达稳定值的时间提前，表明车辆能够更快地到达稳定行驶状态。

图3 横摆角速度曲线

图4为两种控制施加情况下仿真得出的质心侧偏角曲线图。从图4中可以看出，仅使用模型预测轨迹跟踪控制的车辆，在避撞轨迹跟踪过程中质心侧偏角变化较大、曲线变化率较大、震荡时间较长；采用联合控制方法后，车辆的质心侧偏角的绝对值不超过0.05°，曲线变化量得到抑制、曲线变化率明显减小，说明控制器有效提高了车辆行驶过程中的稳定性。

图4 质心侧偏角仿真曲线

图5为两种控制施加情况下仿真得出的前轮转角输出值。由图5可知，仅使用模型预测轨迹跟踪控制的车辆前轮转角变化量较大，跟踪理想轨迹的调整时间长；施加联合控制的车辆，轨迹跟踪过程中调整时间变短，前轮转角变化量减小，车辆前轮能够更快地回正。结合图2也可以发现，施加联合控制的车辆能更快地到达直线行驶轨迹。这表明横摆力矩控制器对模型预测轨迹跟踪控制器起到了较好的辅助作用，能有效提升轨迹跟踪效果。

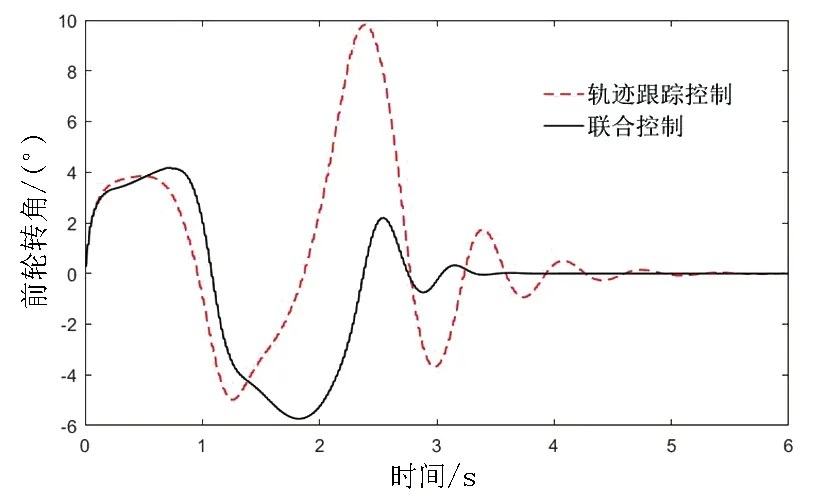
图5 前轮转角仿真曲线

4 结论

本文结合模型预测轨迹跟踪控制与汽车横摆力矩控制实现对避撞轨迹的跟踪。仿真结果表明：

1)在附着系数为0.4的较低附着系数路面条件下，采用增加横摆力矩控制的联合控制方法，提升了模型预测轨迹跟踪控制效果和车辆稳定性。

2)与单一轨迹跟踪控制相比，采用模型预测轨迹跟踪与横摆力矩联合控制后， 车辆能够更快地跟踪到预设直线行驶轨迹，降低前轮转角调整幅值。