考虑寄生电感的谐振开关电容变换器电压尖峰抑制

刘 妍 杨晓峰 闫成章 陈 骞 温 飘,3 五十岚征辉

考虑寄生电感的谐振开关电容变换器电压尖峰抑制

刘 妍1杨晓峰1闫成章1陈 骞2温 飘1,3五十岚征辉4

（1. 北京交通大学电气工程学院 北京 100044 2. 国网浙江省电力有限公司电力科学研究院 杭州 310014 3. 中国科学院光束控制重点实验室 成都 610209 4. 富士电机系统株式会社 东京 141-0032）

基于碳化硅（SiC）器件的谐振开关电容变换器（RSCC）因其软开关特性，适用于高频、高功率密度的场合。但是较高的工作频率使其对线路寄生参数较敏感，易造成开关器件的电压尖峰问题。通过分析RSCC叠层母排模型，该文建立含有寄生电感的等效电路，研究寄生电感对电路运行模态的影响，并推导开关器件电压峰值与寄生电感之间的关系。在此基础上，提出优化叠层母排结构和吸收电容的电压尖峰抑制方案，仿真及实验结果验证了该文电压尖峰抑制方案的有效性和可行性。

谐振开关电容变换器 叠层母排 寄生电感 电压尖峰抑制

0 引言

随着新能源发电、电动汽车以及储能电池等不断发展，直流变换器获得了广泛应用[1-7]。传统直流变换器如Buck、Boost等拓扑控制简单，但其调压能力有限、电压纹波大、运行效率低[8-10]。为此，一系列高性能直流变换器的拓扑被相继提出。开关电容变换器（Switched Capacitor Converter, SCC）具有体积小、质量轻等优势，但SCC开关过程中存在较高的电流尖峰[11-14]。通过引入电感元件与SCC开关电容串联构成谐振单元，即谐振开关电容变换器（Resonant Switched Capacitor Converter, RSCC），使其在开环条件下可实现零电流软开关（Zero Current Switching, ZCS）[13]，有效地减小了开关损耗，提高变换器的工作频率。此外，碳化硅（Silicon Carbide，SiC）器件具有开关频率高、导通电阻低、开关损耗小、耐高温等优点，展现出了良好的应用前景[15-19]。使用SiC器件作为RSCC的开关器件，可进一步提升其工作频率及运行效率。

随着RSCC工作频率的提高，寄生电感对其工作模态的影响不可忽略，文献[20]分析了寄生电感对开关电流尖峰的影响，而未考虑其对电压尖峰的影响。事实上，寄生电感对开关电压的影响同样显著，文献[21-24]中均存在不同程度的电压尖峰及振荡现象，随着开关频率增加，该现象将更加明显。此外，由于SiC器件的结电容小，对线路寄生参数更为敏感，高频工作时将承受更大的开关应力，影响开关寿命，甚至造成永久性损坏[25-26]。同时，开关器件的结电容与电路中的寄生电感相互作用产生高频振荡，增大了电路损耗及电磁干扰问题。

为减小寄生电感对RSCC的影响，本文采用叠层母排作为线路连接部件。叠层母排结构紧凑，其高频电流趋肤效应能有效减小功率回路中的寄生电感，抑制开关器件的电压尖峰[27-30]。然而叠层母排中的寄生电感不可避免，文献[31]分析了叠层母排寄生电感的影响因素，为母排的低电感设计提供了参考。文献[32]分析了叠层母排寄生电感对混合钳位变流模块电容电流的影响，但未从数学角度对其造成的开关电压尖峰定量分析。

本文在分析RSCC工作原理的基础上，结合叠层母排有限元仿真提取的寄生参数，建立了含寄生电感的等效电路；推导了寄生电感与开关器件电压尖峰之间的关系；然后提出了电压尖峰的抑制方案；最后搭建了仿真及实验电路，验证了等效电路及所提出解决方案的正确性和有效性。

1 谐振开关电容变换器

图1为典型的RSCC电路拓扑，包含两个模块化谐振开关电容单元（Modular Resonant Switched Capacitor Cell, MRSCC），分别称为MRSCC1和MRSCC2。每个谐振单元均包含四个开关器件，即S1、S2、S3、S4（=1, 2），其中，两个开关半桥之间均由谐振腔Lr及Cr连接。RSCC的关键波形如图2所示，在一个开关周期s内，S1与S2分别以50%的占空比交替导通。ir为谐振腔的电流，ur为谐振电容电压，其参考方向如图1所示。为避免结电容放电造成的谐振电流阶跃以及硬开关问题，使S3、S4分别与S1、S2同时开通，且S3及S4的开通时间q应大于S3（S4）的结电容放电时间f1，f1可表示[33]为

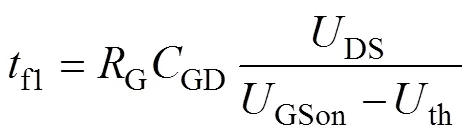
式中，RG为驱动电阻；CGD为栅-漏极电容；UDS为开关Sj3（Sj4）的漏源极电压初值；UGSon为驱动正电压；Uth为MOSFET的开通电压。

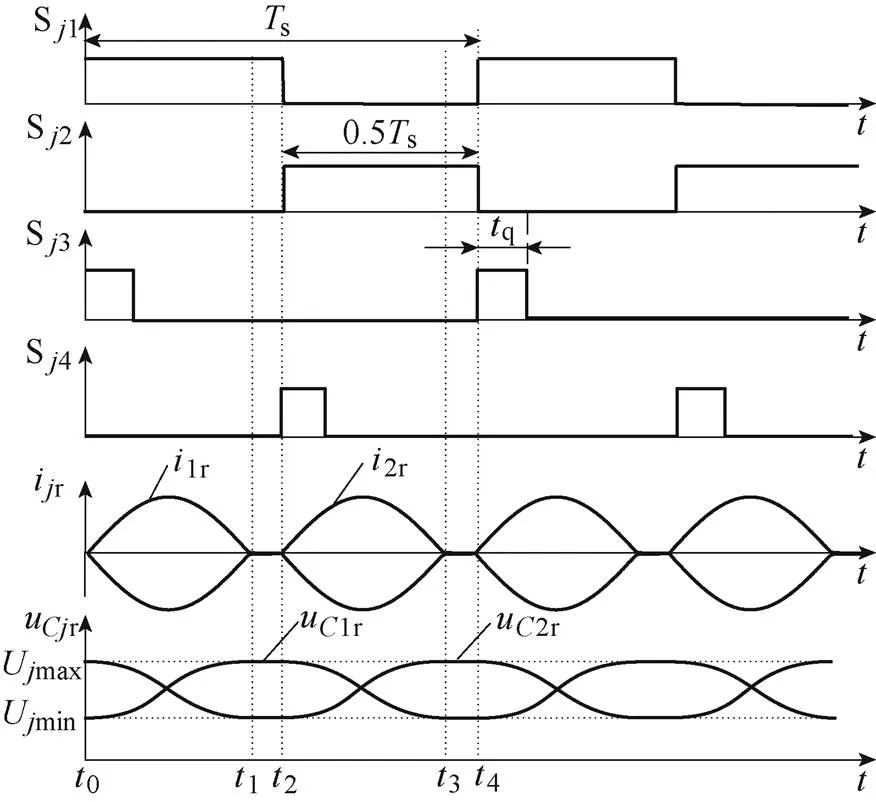
图2 RSCC关键波形

此外S3（S4）应在谐振电流过零之前关断，即二者的开通时间应小于谐振周期r的一半，阻断谐

振电流反向流动。由于SiC器件结电容较小，放电速度较快，本文选取S3及S4的导通时间为10%r。

为了实现ZCS，开关器件需要在谐振电流为零后关断，即谐振频率r应大于开关频率s。因此，在一个开关周期内共有四种运行模态，其等效电路如图3所示。为简化分析，做如下假设：

（1）直流电容足够大，直流侧电压恒定。

（2）所有元件均为理想元件。

（3）正负谐振单元参数一致，即1r=2r=r，1r=2r=r。

（4）电路已工作在稳定状态。

模态1 [0,1]：0时刻，S3的结电容通过S3放电。S11及S13的反并联二极管VDS13实现ZCS开通，由1向MRSCC1的谐振腔传递能量，在此过程中1r的电压从1min逐渐增大；同时在MRSCC2中，S21及S23的反并联二极管VDS23实现ZCS开通，由谐振腔向输出电容2传递能量，2r的电压从2max逐渐减小，等效电路如图3a所示。

图3 RSCC工作模态等效电路

模态2 [1,2]：1时刻，谐振电感的电流谐振至零，VDSj3关断，在此过程中，谐振回路与直流电容之间无能量传输，谐振电流ir保持为零，u1r与u2r则分别保持1max与2min恒定，直到半个开关周期结束，如图3b所示。

模态3 [2,3]：2时刻，S4的结电容通过其开关放电，S2及S4的反并联二极管VDSj4实现ZCS开通，能量开始反向流动。在此过程中，1r的电压从1max逐渐减小；同时在MRSCC2中，直流电容3向其谐振单元传递能量，2r的电压从2min逐渐增大，如图3c所示。

模态4 [3,4]：谐振电流再次谐振至零，所有二极管均被关断，谐振电流ir保持为零，u1r与u2r则分别保持1min与2max恒定，直到整个开关周期结束，此模态等效电路如图3b所示。

通过上述分析可知，在理想情况下，可以实现开关器件的零电流开通。但由于电路寄生电感的存在，易与开关结电容之间产生高频振荡，造成开关器件的电压尖峰。

2 寄生电感与电压尖峰分析

2.1 叠层母排寄生电感

本文选用叠层母排作为RSCC的主电路连接部件。图4a为RSCC主电路的一种叠层母排的结构模型，称为母排一，采用四个半桥模块M1、M2、M3及M4作为功率开关器件，分别对应图1中的四个开关半桥，对应关系如图4标注。模型中一共有四层母排，分别称为I1、I2、O1、O2。

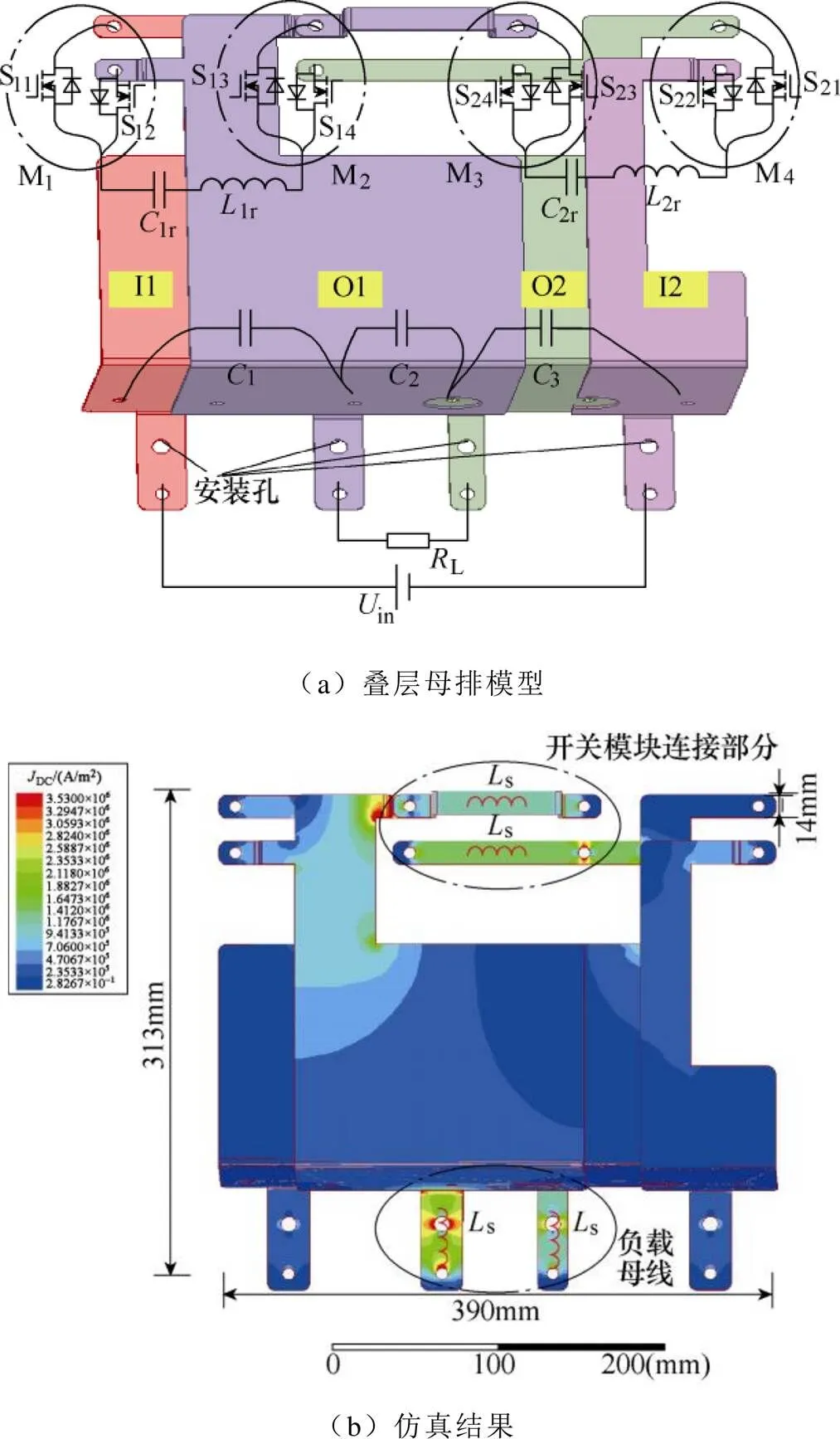
图4 RSCC母排一模型

在Ansys Q3D软件中对其进行有限元仿真，如图4b所示。可以看到，负载母线以及M2、M3之间连接铜条上的表面电流密度明显大于其他处，表明此处寄生电感更大。从第1节分析中可知，负载母线上的寄生参数对开关运行影响较小，为简化分析，本文仅考虑了两个铜条上的寄生电感。图5所示为考虑寄生电感的RSCC拓扑，图5中标注了各母排所对应的位置。

2.2 电压尖峰分析

考虑寄生电感时的关键波形如图6所示，为简化分析，假设开关器件完全相同，其结电容均为s，且线路上的寄生电感均为s。

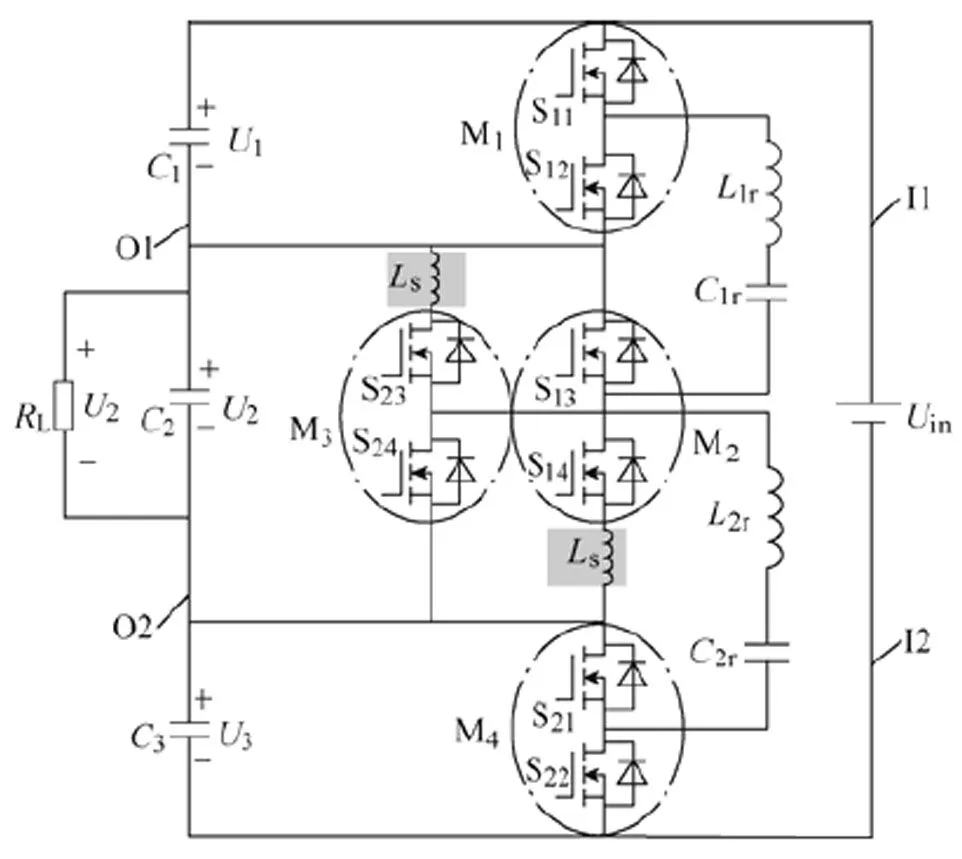
图5 考虑寄生电感的RSCC拓扑

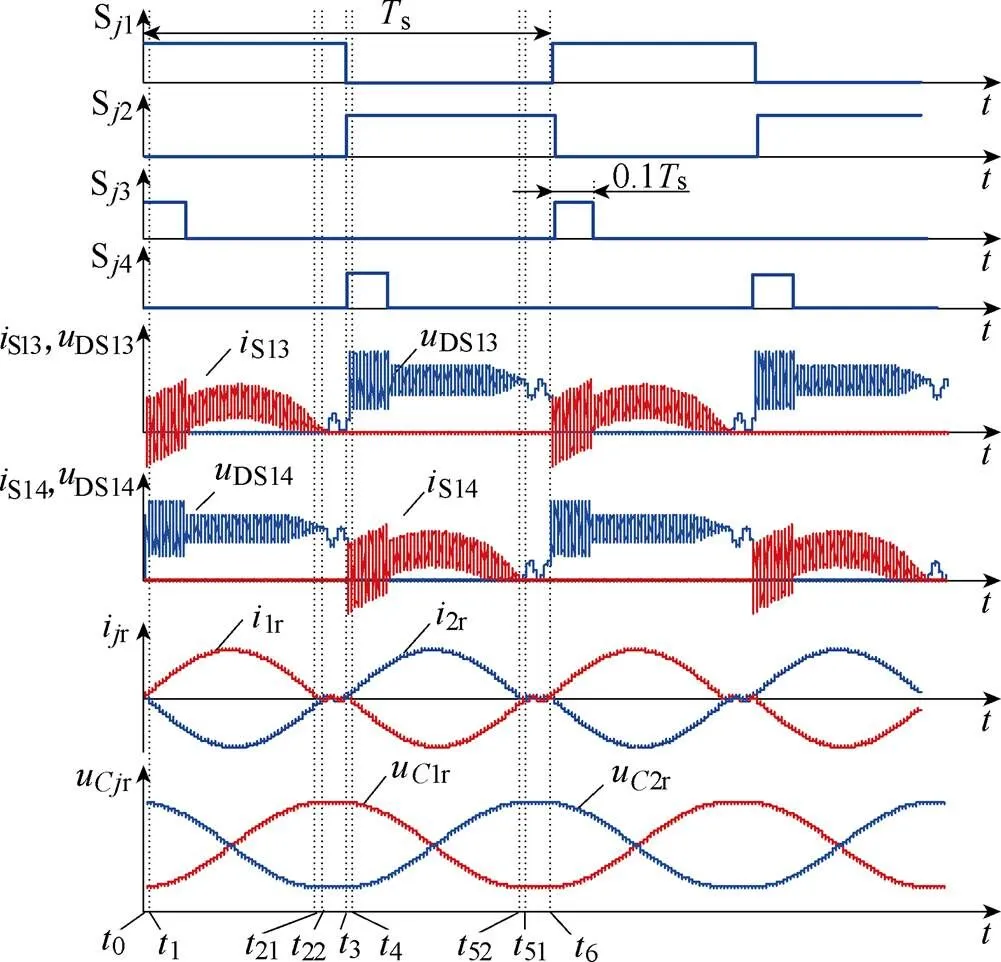
图6 考虑寄生电感的关键波形

在一个开关周期内，RSCC一共具有六个运行模态，如图7所示。图中，上半开关周期为工作模态一至模态三，下半开关周期为模态四至模态六。由于上、下半个周期的工作模态对称，不失一般性，本文以上半个开关周期的三个运行模态为例展开详细分析。

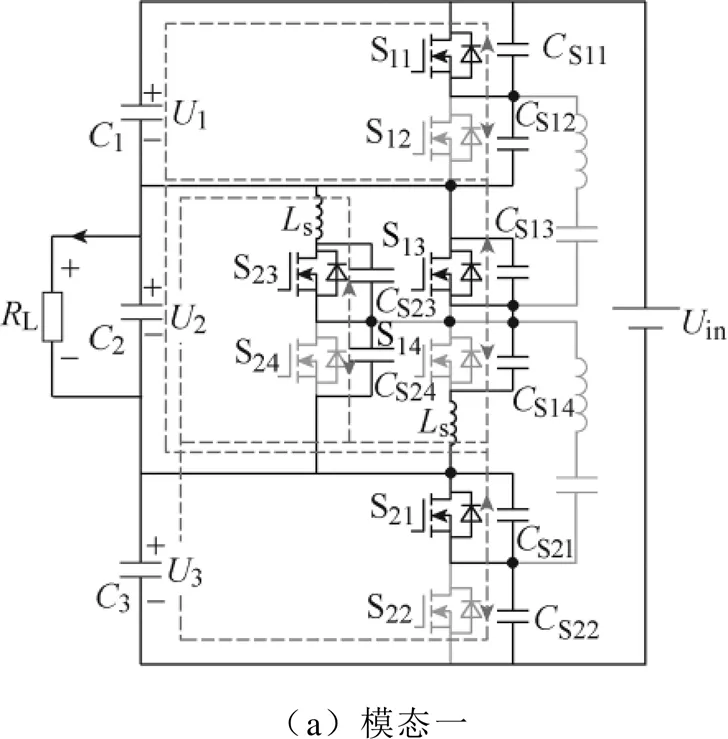
图7 RSCC运行模态

模态一[0,1]：电压电流波形及等效电路如图8所示。0时刻，S1及S3导通，S3的结电容通过S3放电，同时S4的结电容充电。此时S3的二极管被钳位而无法导通，此模态的边界值为ir(0)=0，u1r(0)=1min，u2r(0)=2max，DSj3(0)=DS31，DSj4(0)=DS41。在此阶段内，S13及S14的电压及电流波形如图8a所示。

图8 模态一电压1电流波形及等效电路

在此阶段内，S3的电压下降，可将其等效为一个电压源eq，等效电路如图8b所示。分析图中d/d的瞬态过程，则eq可表示为

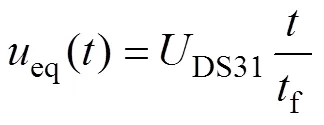
式中，f为S3电压下降至0所需的时间，即eq的电压上升至DS31所需要的时间，从而可以得到S14的电压及寄生电感电流为

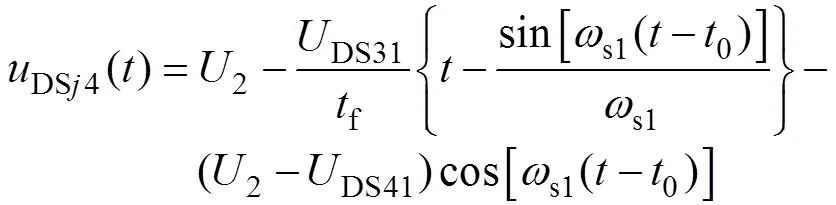
模态二[1,2j]：等效电路如图9所示。在1时刻S3的电压下降至0，VDSj3导通。在此期间MRSCC1通过S11及S13充电，MRSCC2通过S21及S23放电，如图7b所示。主谐振回路可以简化为图9a所示的等效电路，此模态的边界值为ir(1)=Ir1，u1r(1)=1min，u2r(1)=2max，DSj3(1)=0，Sj3(1)=Sj3，DSj4(1)=DS42。在此阶段内，由于开关结电容对谐振电流的影响较小，为简化分析，可将MRSCC2的等效电路拆分为如图9b所示的主谐振回路和寄生谐振回路，从而求得谐振电流近似为

其中

图9 模态二等效电路

同理求得S3的电流及S4的电压分别为

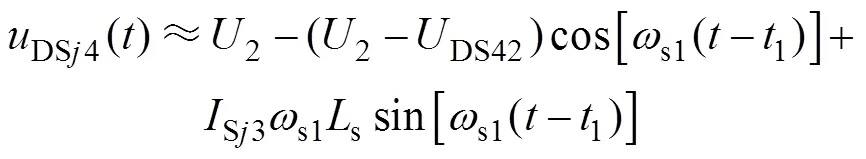
由上述分析可以得知，在模态二中，MRSCC1的谐振周期为2prr，而MRSCC2的谐振周期为2p(r+s)r，在图6中可以看到，MRSCC1的谐振电流先于MRSCC2至零。在模态五中，二者的谐振周期关系恰好相反，MRSCC2的谐振电流会先于MRSCC1至零。

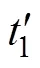
图10 模态二关键波形

模态三[2j,3]：在2j时刻，谐振电流减小至0，S1导通，反并联二极管VDSj3阻断谐振电流。如图7c所示，S3的结电容参与谐振。分析电路易知，此模态各变量的边界值为ir1(2j)=ir2(2j)=ir(2j)=0，u1r(2j)=1min+D1，u2r(2j)=2max-D2，DSj3(2j)=0，DSj4(2j)=2。由模态二易知，对于MRSCC1，21=0+p/r1，而对于MSCC2，22=0+p/r2，可得谐振电流为

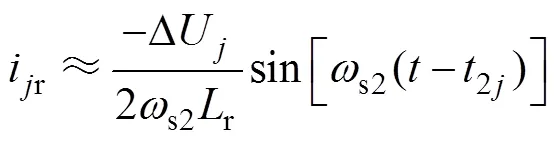
进而求得各结电容的电压为

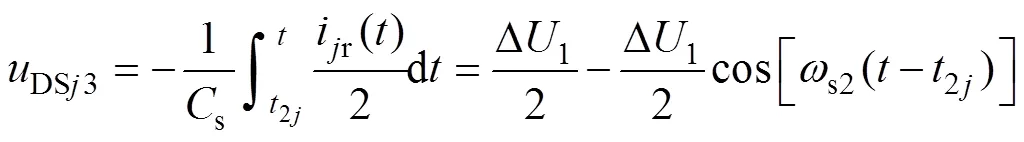
式中，s2为开关电压的振荡频率，s2≈(2rs)-1/2。

综合上述分析可知，开关S4的电压峰值出现在模态二中，此模态中的电压可表示为

其中

在一个开关周期内，开关器件的电压尖峰可表示为p=2+。绘制电压尖峰标幺值与寄生电感之间的关系如图11所示，图中，pN=p/2。可以看到，开关电压尖峰与寄生电感有关，随着寄生电感的增大，开关电压尖峰上升。当寄生电感较大时，开关器件的电压尖峰可能超过1.5倍的额定电压。而在电路设计中，通常选取开关器件的耐压值为1.2～1.5倍的额定电压，当器件承受的电压过高时，可能会影响开关器件的工作寿命，严重时甚至会造成开关器件的永久性损坏。因此，有必要对寄生电感造成的开关电压尖峰进行抑制。

图11 开关器件电压尖峰

3 电压尖峰抑制

根据上述分析，本文拟采用两种方法对其进行抑制：①通过优化叠层母排结构减小其寄生电感；②通过优化吸收电容抑制开关电压尖峰及高频振荡。

3.1 母排结构优化

在低感叠层母排设计中，应尽量使正、负极母排电流产生的磁场相互抵消，减小非叠层部分的面积，从而达到减小寄生电感的目的。

本文优化了叠层母排结构，增大了正、负极母排之间的叠层面积，并对其接线端子做加宽处理，形成母排二的结构如图12所示。为验证叠层母排的优化效果，在ANSOFT Q3D中对母排二进行了有限元仿真，如图12b所示，可以看到，寄生电感仍然集中在负载母线以及M2、M3的连接部分上，但优化后开关模块连接部分的表面电流密度降低，表明该部分的寄生电感减小。

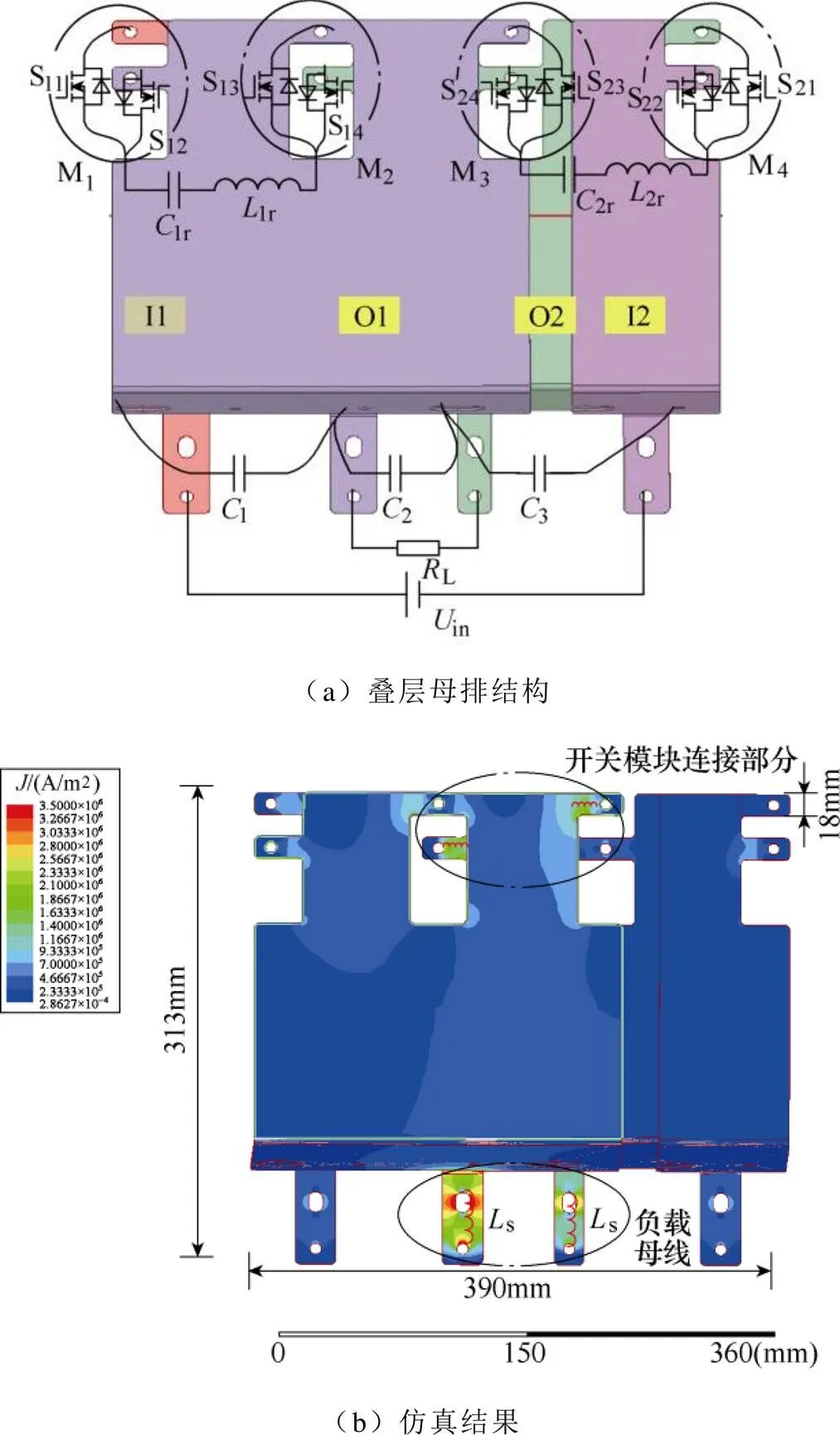
图12 母排二结构

在Ansys Q3D软件中对两个叠层母排的寄生电感进行仿真分析，其中电路的“source”与“sink”根据电路中电流的实际流向选取。仿真得到母排一的输出母排O1及O2的寄生电感分别为32.014nH、41.616nH，而在母排二中，寄生电感值分别为12.353nH、23.164nH。可以看到，叠层母排二的寄生电感相比母排一减小了52%左右。

3.2 吸收电容优化

鉴于优化后的叠层母排寄生电感仍不可避免，通过在开关半桥两端并联吸收电容的方法亦可达到尖峰抑制效果。加入吸收电容后的RSCC电路如图13所示，图中，a1、a2、a3、a4为吸收电容，四个电容的容值相等，均为a。加入吸收电容之后，仍可将电路运行分为六个运行模态，不失一般性，对上半周期的三个模态进行分析。

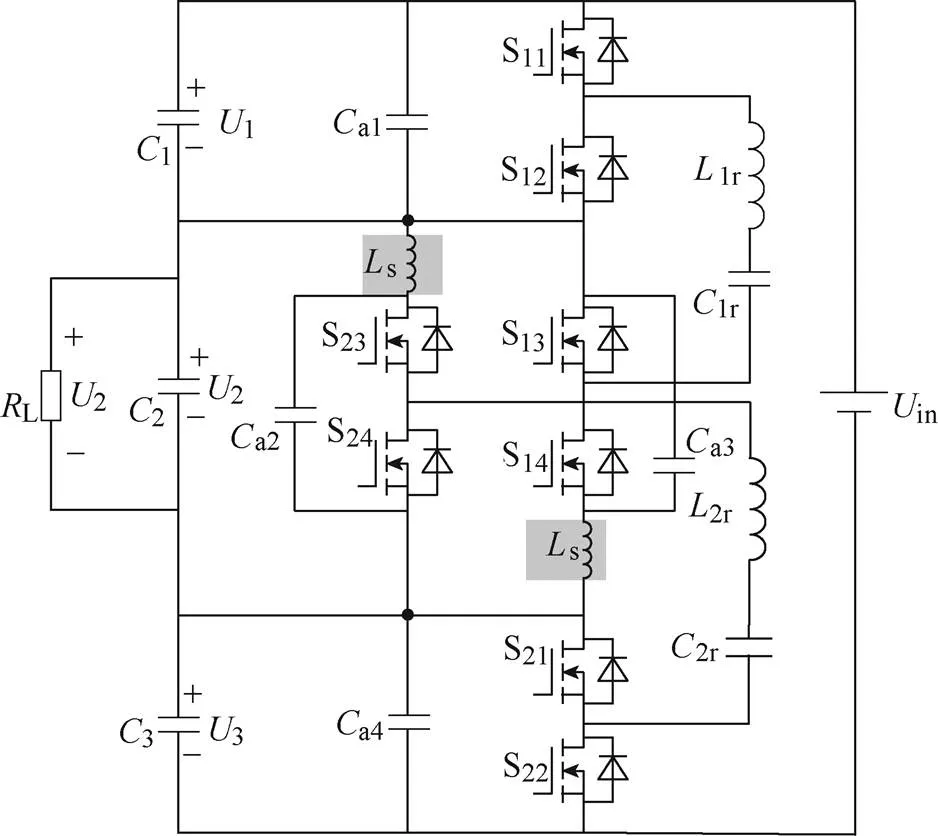
图13 加入吸收电容的RSCC电路

模态Ⅰ[0,1]：0时刻，S3的结电容放电，同时S4的结电容充电。记此模态的吸收电容的边界值为a1，且DSj3(0)=DS31，DSj4(0)=DS41。则在此阶段内的S4结电容电压可表示为

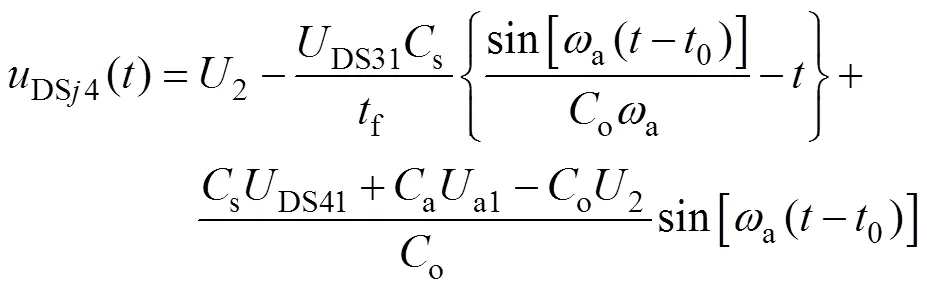
同理得吸收电容的电压为

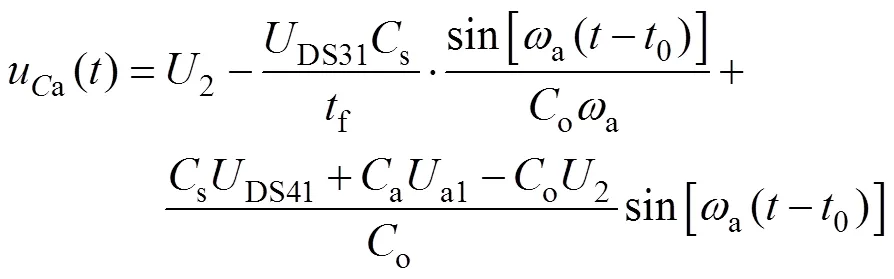
式中，o为结电容与吸收电容并联后的容值，o=a+s；a为开关的振荡频率，a=(so)-1/2。由于开关器件的结电容较小，当模态一结束时，ua与DSj4近似相等。

模态Ⅱ[1,2j]：记此模态吸收电容与结电容电压均为DS42，在此阶段内结电容与吸收电容并联的等效电容与寄生电感组成振荡电路，此振荡将持续至整个模态结束，则开关器件的结电容电压可近似表示为

可以看到，在吸收电容的作用下，模态二中的开关电压振荡频率由原来的s1减小为a，这表明吸收电容具有抑制开关电压振荡的作用。

模态Ⅲ[2j,3]：2j时刻，谐振电流减小至零，在此模态内吸收电容对主电路的运行影响较小，可近似认为主电路的运行模态不变，而吸收电容则与寄生电感共同组成振荡回路，记吸收电容的电压初值为DS43，可将其电压表示为

本文分别选取了0.047mF、0.47mF与4.7mF三组吸收电容，加入吸收电容后的开关电压如图14所示。可以看到，三组吸收电容均具有一定的吸收效果，开关器件的电压尖峰明显减小，振荡周期增长，振荡现象减轻。此外，吸收电容越大，吸收效果越好，但吸收电容进一步增大时，开关器件的电压尖峰及振荡现象无明显改善。考虑到吸收电容的体积及成本，选取吸收电容为0.47mF，即可达到较好的电压尖峰吸收效果。

为验证吸收电容的优化效果，本文搭建了相应的仿真。设置输入电压为600V，输出功率为6.7kW，开关频率为40kHz，谐振电感及电容分别为3mH和4mF，开关结电容为5nF。图14b为寄生电感为10～300mH，吸收电容为0.47mF时的开关电压尖峰，当寄生电感增大时，开关电压尖峰均保持在1.05倍的额定电压以内，实现了较好的优化作用。

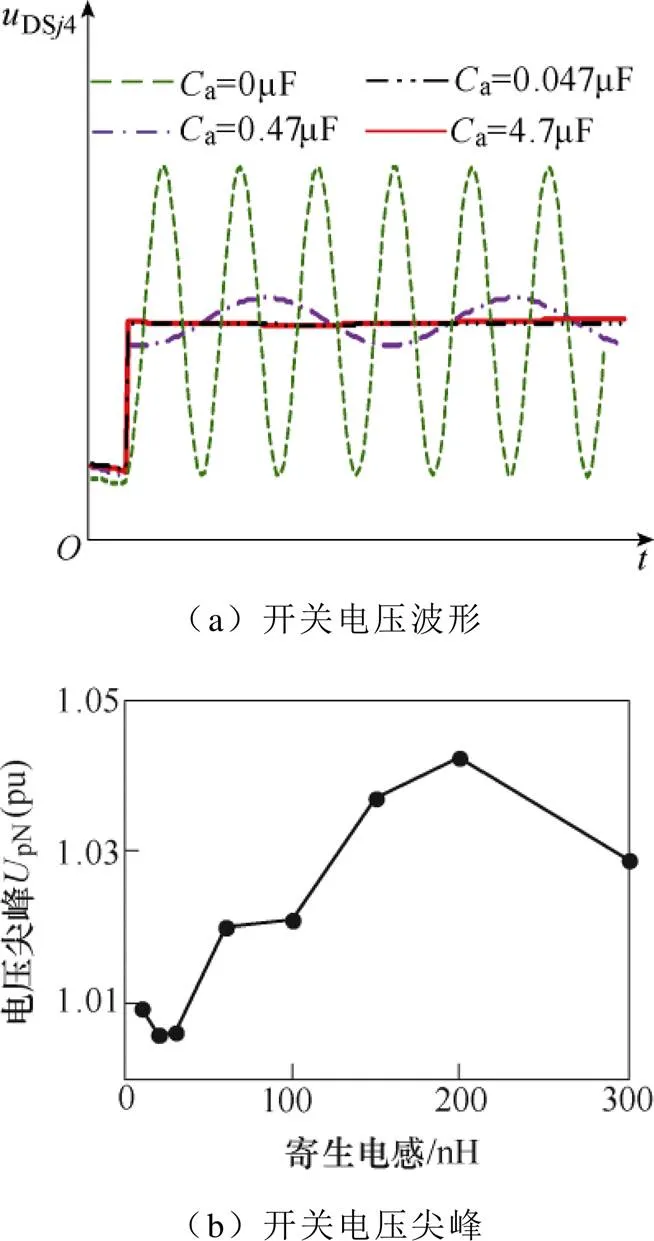
图14 加入吸收电容后的开关电压波形

4 仿真及实验验证

4.1 仿真验证

为验证上述理论分析的正确性，本文搭建了如图5所示的仿真模型，对RSCC开关器件电压尖峰及其抑制方法的有效性进行验证，仿真参数见表1。

表1 RSCC仿真参数

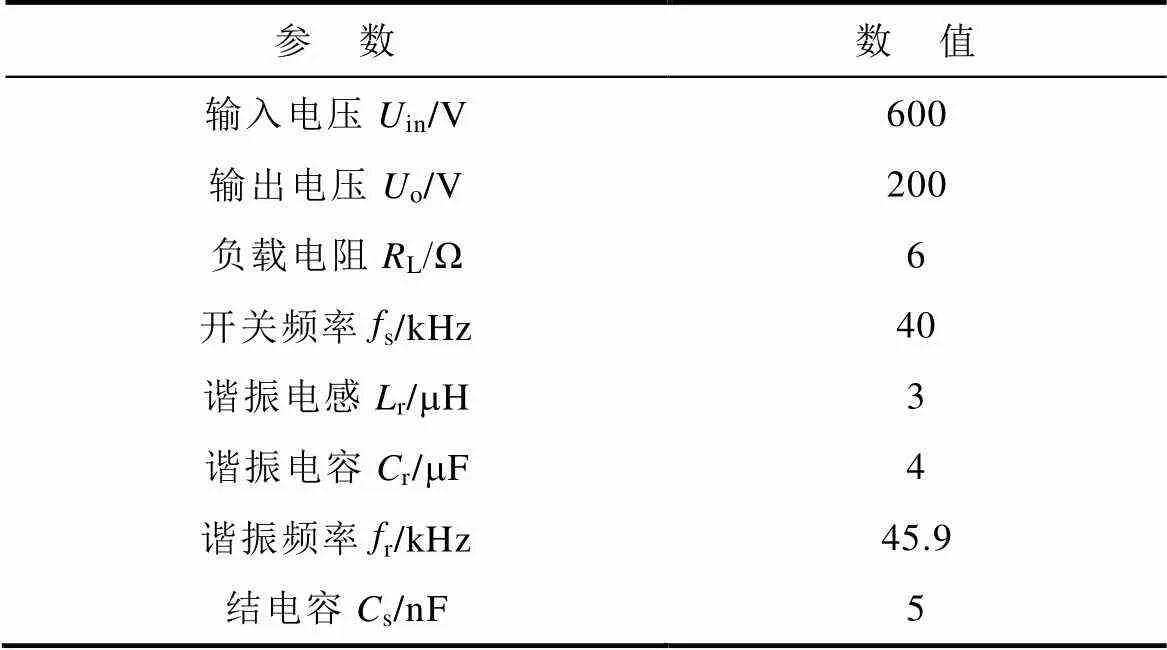
Tab.1 Simulation parameters of RSCC

首先选取电路寄生电感为10～300nH，记录不同寄生电感作用下的开关电压尖峰值，并与计算结果进行对比，如图15所示。可以看到，当寄生电感增大时，电压尖峰随之增大。仿真结果与计算结果的变化趋势基本一致，电压尖峰的曲线基本吻合，这表明本文所推导的数学模型具有一定的准确性。

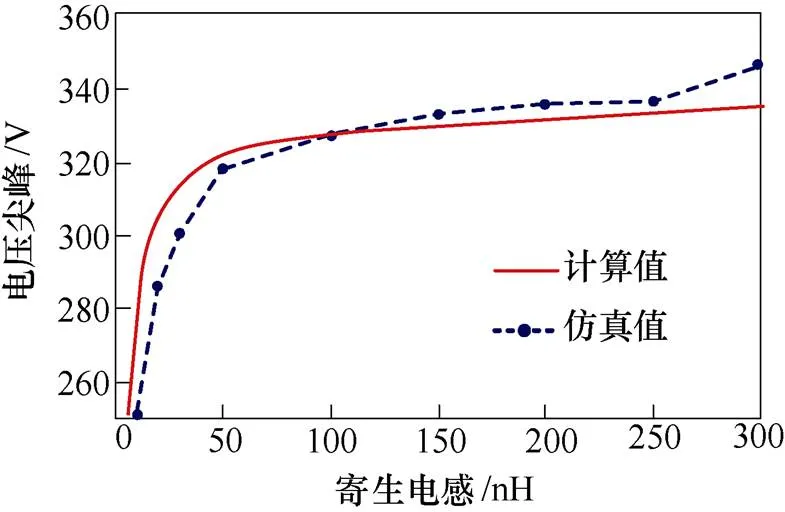
图15 电压尖峰值对比

设置寄生电感为100nH，S3及S4导通时间均为10%s。仿真得到的谐振电流波形如图16所示。可以看到，由于寄生电感分布位置的差异，上、下谐振单元的谐振周期略有不同，当S1导通时，上谐振单元的谐振周期更短；当S2导通时，下谐振单元的谐振周期更短，二者谐振周期的差异约为0.5ms，这种现象与理论分析的结果基本一致。

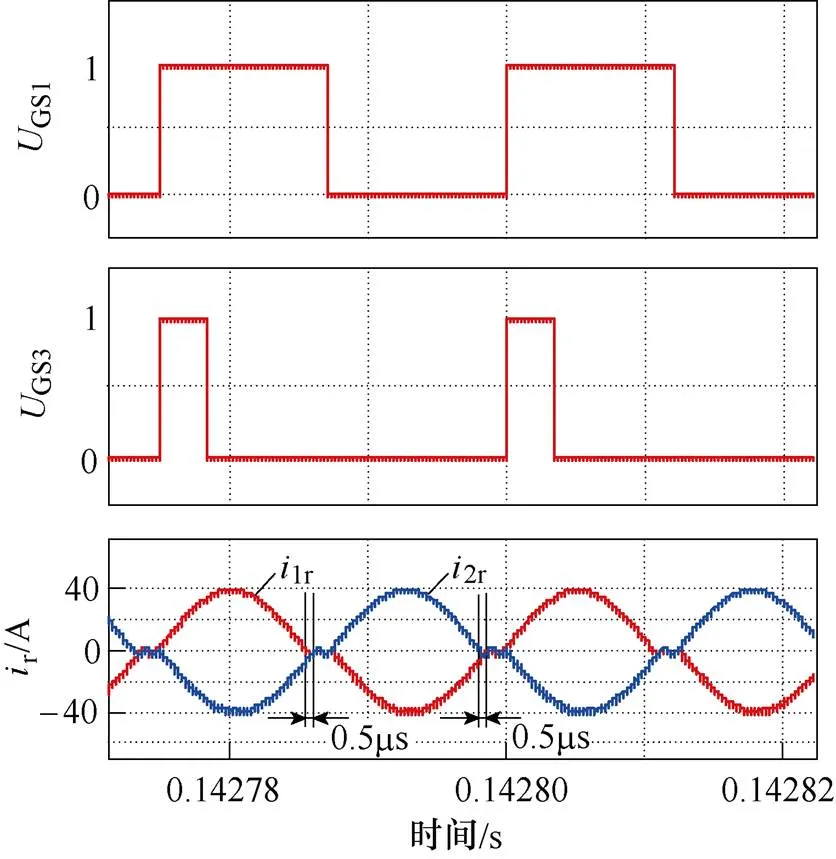
图16 谐振电流波形

图17为电压尖峰仿真波形。可以看到，当S13开通时，在S14中产生了较大的电压尖峰，同时伴随高频振荡。测量可得，开关器件的电压尖峰为327V，振荡频率为7.121MHz，与理论分析结果基本一致。

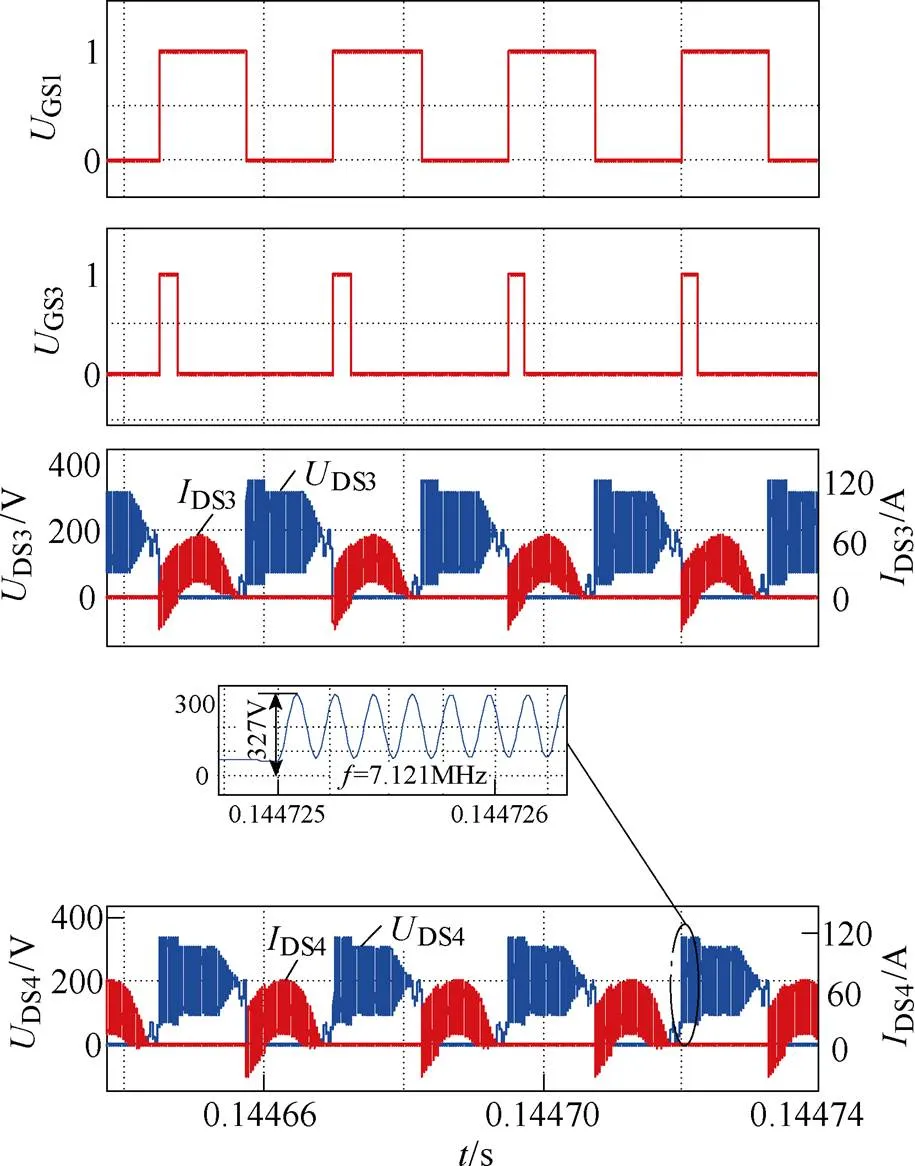
图17 电压尖峰仿真波形

在开关半桥两端并联容值为0.47mF的吸收电容，仿真波形如图18所示。可以看到，S14电压的最大值为206V，仅为未加入吸收电容时电压尖峰的62%左右。此外，振荡频率减小至746kHz，与理论分析结果相符。仿真结果表明，本文所选取的吸收电容对开关电压尖峰具有良好的吸收效果，且对其电压振荡现象具有一定的抑制作用。

图18 加入吸收电容的仿真波形

4.2 实验验证

基于上述分析，根据图1搭建了实验平台，电路元件参数见表1。本文采用半桥SiC MOSFET模块作为功率开关器件，母排一与母排二的实物模型如图19所示。

图19 叠层母排模型

图20a及图20b分别为母排一及母排二的开关驱动波形以及谐振电流波形。可以看到，由于寄生电感分布不对称，两个叠层母排中均出现了谐振电流不对称的现象。此外，由于母排一中寄生电感的影响，在开关驱动波形中出现串扰现象。而在母排二中，串扰现象几乎消失。

图20 驱动及谐振电流波形

图21a为采用母排一的实验结果，可以看到，由于寄生电阻的存在，开关电压及电流更早地出现了衰减现象。在开关切换过程中，其两端电压存在高频振荡现象，开关器件的电压尖峰值达326V。

图21b为采用母排二的实验结果，可以看到，电压尖峰减小至218V，仅为采用母排一时电压尖峰的65%左右，电压振荡现象有明显改善。

图21 实验结果

图22为在母排二的基础上加入0.47mF吸收电容的实验结果，测得电压尖峰为210V。与母排一的实验结果相比，电压尖峰减小110V以上，电压尖峰值减小35%左右。与未加入吸收电容相比，开关电压尖峰减小3%，表明本文所选取的吸收电容具有一定的尖峰抑制效果。

图22 加入吸收电容的实验结果

5 结论

本文分析了RSCC电路产生电压尖峰及高频振荡的原因。通过对叠层母排的分析，建立了含有寄生电感的等效电路，推导了寄生电感与开关电压尖峰之间的关系，提出了相应的解决方案，并对其进行了仿真及实验验证，结果表明：

1）开关器件的电压尖峰与电路中的寄生电感有关，寄生电感越大，开关器件的电压尖峰越高。

2）通过减小叠层母排中的寄生电感，以及在开关模块两端加入吸收电容等，可以有效地减小开关器件中的电压尖峰，改善电压振荡现象，提高电路运行的可靠性。

致谢：本文作者衷心感谢日本富士电机株式会社所提供的资料信息及相关资助。

[1] Shanbog N S, Pushpa K R. Double input Boost/ Y-source DC-DC converter for renewable energy sources[C]//2nd International Conference on Power and Embedded Drive Control (ICPEDC), Auckland, 2019: 1-6.

[2] Matsumori H, Kosaka T, Sekido K, et al. Isolated DC-DC converter utilizing GaN power device for automotive application[C]//IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 2019: 1704-1709.

[3] Han Byung-Moon. Grid-tied power converter for battery energy storage composed of 2-stage DC-DC converter[C]//IEEE Power & Energy Society General Meeting, Vancouver, BC, 2013: 1-5.

[4] 冷明全, 程为彬, 刘峰, 等. 光伏发电系统前级宽输入DC/DC Boost变换器[J]. 电气传动, 2020, 50(3): 37-39.

Leng Mingquan, Cheng Weibin, Liu Feng, et al. DC/DC Boost converter with wide input voltage in photovoltaic power generation system as pre-stage[J]. Electric Drive, 2020, 50(3): 37-39.

[5] 年珩, 叶余桦. 三端口隔离双向DC-DC变换器模型预测控制技术[J]. 电工技术学报, 2020, 35(16): 3478-3488.

Nian Heng, Ye Yuhua. Model predictive control of three-port isolated bidirectional DC-DC converter[J]. Transactions of China Electrotechnical Society, 2020, 35(16): 3478-3488.

[6] 杨东江, 段彬, 丁文龙, 等. 一种带辅助双向开关单元的宽输入电压范围LLC谐振变换器[J]. 电工技术学报, 2020, 35(4): 775-785.

Yang Dongjiang, Duan Bin, Ding Wenlong, et al. An improved LLC resonant converter with auxiliary bi-directional switch for wide-input-voltage range applications[J]. Transactions of China Electrotech- nical Society, 2020, 35(4): 775-785.

[7] Zhang Yixuan, Chen Guipeng, Hu Yihua, et al. Cascaded multilevel inverter based power and signal multiplex transmission for electric vehicles[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(2): 123-129.

[8] 李楠, 王萍, 贝太周, 等. 新型高增益开关电容直流升压变换器[J]. 电力系统及其自动化学报, 2017, 29(6): 83-89.

Li Nan, Wang Ping, Bei Taizhou, et al. Novel high-voltage gain switched-capacitor DC-DC Boost converter[J]. Proceedings of the CSU-EPSA, 2017, 29(6): 83-89.

[9] 侯世英, 陈剑飞, 孙韬, 等. 基于Switch-Capacitor网络的单开关升压变换器[J]. 电工技术学报, 2013, 28(10): 206-216.

Hou Shiying, Chen Jianfei, Sun Tao, et al. A single- switch step-up converter based on Switch-Capacitor network[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 206-216.

[10] 谢子殿, 艾建. 一种基于开关电感电容技术的耦合电感升压变换器[J]. 黑龙江科技大学学报, 2015, 25(6): 670-675.

Xie Zidian, Ai Jian. A novel high step-up converter with a switched-coupled-inductor-capacitor structure[J]. Journal of Heilongjiang University of Science and Technology, 2015, 25(6): 670-675.

[11] 雷浩东, 郝瑞祥, 游小杰, 等. 基于开关电容和三绕组耦合电感的高电压增益DC-DC变换器[J]. 电工技术学报, 2020, 35(17): 3666-3677.

Lei Haodong, Hao Ruixiang, You Xiaojie, et al. High voltage gain DC-DC converter with switched- capacitor and three-winding coupled inductor[J]. Transactions of China Electrotechnical Society, 2020, 35(17): 3666-3677.

[12] 李永东, 徐杰彦, 杨涵棣, 等. 多电平变换器拓扑结构综述及展望[J]. 电机与控制学报, 2020, 24(9): 1-12.

Li Yongdong, Xu Jieyan, Yang Handi, et al. Overview and prospect of multilevel converter topology[J]. Electric Machines and Control, 2020, 24(9): 1-12.

[13] Shoyama M, Ninomiya T. Output voltage control of resonant Boost switched capacitor converter[C]//Power Conversion Conference, Nagoya, 2007: 899-903.

[14] Salehian A, Hashemi S S, Beiranvand R, et al. Simulation of a step-up resonant switched-capacitor converter under the CCM operation mode[C]//10th International Power Electronics, Drive Systems and Technologies Conference (PEDSTC), Shiraz, Iran, 2019: 230-235.

[15] 刘瑞煌, 杨景刚, 贾勇勇, 等. 中压直流配电网中直流变压器工程化应用[J]. 电力系统自动化, 2019, 43(23): 131-140.

Liu Ruihuang, Yang Jinggang, Jia Yongyong, et al. Engineering applications of DC transformer in medium- voltage DC distribution network[J]. Automation of Electric Power Systems, 2019, 43(23): 131-140.

[16] Ino K, Miura M, Nakano Y, et al. SiC power device evolution opening a new era in power electronics[C]// IEEE International Conference on Electron Devices and Solid-State Circuits (EDSSC), Xi’an, China, 2019: 1-3.

[17] Imaizumi M, Hasegawa S, Sumitani H, et al. Remarkable advances in SiC power device technology for ultra high power systems[C]//IEEE International Electron Devices Meeting, Washington, DC, 2013: 1-4.

[18] Okuda T, Nakamura Y, Hikihara T, et al. Analysis of transient behavior of SiC power MOSFETs based on surface potential model and its application to Boost converter[C]//IEEE 4th Workshop on Wide Bandgap Power Devices and Applications (WIPDA), Fayetteville, AR, 2016: 101-104.

[19] 史方圆, 李睿, 蔡旭. 35kV全SiC光伏发电单元中高频隔离变换器的寄生参数影响及抑制方法[J]. 中国电机工程学报, 2020, 40(6): 1787-1801.

Shi Fangyuan, Li Rui, Cai Xu. Influence of parasitic parameters and its suppression methods of high frequency isolated converter in 35kV all-SiC photo- voltaic generation unit[J]. Proceedings of the CSEE, 2020, 40(6): 1787-1801.

[20] 王淼, 杨晓峰, 郑琼林. 谐振开关电容变换器中硬开通问题[J]. 电工技术学报, 2019, 34(增刊1): 154-162.

Wang Miao, Yang Xiaofeng, Zheng Trillion Q. The hard turning-on problems of resonant switched capacitor converter[J]. Transactions of China Electro- technical Society, 2019, 34(S1): 154-162.

[21] Taghziadeh H, Cross A M. The effect of circuit parasitics on resonant switched capacitor converters[C]// 17th European Conference on Power Electronics and Applications (EPE'15 ECCE-Europe), Geneva, 2015: 1-9.

[22] Beiranvand R. Analysis of a switched-capacitor converter above its resonant frequency to overcome voltage regulation issue of resonant SCCs[J]. IEEE Transactions on Industrial Electronics, 2016, 63(9): 5315-5325.

[23] 梅纯. 开关电容变换器的研究[D]. 武汉: 华中科技大学, 2007.

[24] 周宇豪. 模块化多电平谐振式DC-DC变换器的研究[D]. 北京: 北京交通大学, 2019.

[25] 周志达, 葛琼璇, 赵鲁, 等. 碳化硅器件建模与杂散参数影响机理[J]. 电机与控制学报, 2020, 24(1): 27-37.

Zhou Zhida, Ge Qiongxuan, Zhao Lu, et al. Modeling of SiC power device and study of nonlinear stray parameters impact[J]. Electric Machines and Control, 2020, 24(1): 27-37.

[26] 王莉娜, 马浩博, 袁恺, 等. SiC MOSFET半桥电路开关瞬态过电流、过电压建模与影响因素分析[J]. 电工技术学报, 2020, 35(17): 3652-3665.

Wang Lina, Ma Haobo, Yuan Kai, et al. Modeling and influencing factor analysis of SiC MOSFET half- bridge circuit switching transient overcurrent and overvoltage[J]. Transactions of China Electrotech- nical Society, 2020, 35(17): 3652-3665.

[27] 朱俊杰, 原景鑫, 聂子玲, 等. 基于全碳化硅功率组件的叠层母排优化设计研究[J]. 中国电机工程学报, 2019, 39(21): 6383-6393.

Zhu Junjie, Yuan Jingxin, Nie Ziling, et al. Optimum design of planer busbar based on all-silicon carbide power module[J]. Proceedings of the CSEE, 2019, 39(21): 6383-6393.

[28] Yuan Zhao, Peng Hongwu, Deshpande A, et al. Design and evaluation of laminated busbar for three- level T-type NPC power electronics building block with enhanced dynamic current sharing[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2020, 8(1): 395-406.

[29] Wang Zhongjing, Wu Yuheng, Mahmud M, et al. Busbar design and optimization for voltage overshoot mitigation of a silicon carbide high-power three-phase T-type inverter[J]. IEEE Transactions on Industrial Electronics, 2021, 36(1): 204-214.

[30] Lu Binxian, Pickert V, Hu Junzhou, et al. Deter- mination of stray inductance of low-inductive laminated planar multiport busbars using vector synthesis method[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 1337-1347.

[31] 李广卓. 大容量变流器叠层母排杂散电感性能分析[D]. 杭州: 浙江大学, 2019.

[32] 董玉斐, 罗皓泽, 杨贺雅, 等. 1.2MV·A混合钳位五电平变流模块的结构布局优化和叠层母排设计[J]. 电工技术学报, 2016, 31(8): 11-18.

Dong Yufei, Luo Haoze, Yang Heya, et al. Enginee- ring design for structure and bus bar of 1.2MV·A hybrid clamped five-level converter module[J]. Transactions of China Electrotechnical Society, 2016, 31(8): 11-18.

[33] 郑丹, 张少昆, 李磊, 等. SiC MOSFET开关损耗测试方法研究[J]. 中国电机工程学报, 2020, 40(9): 2975-2983.

Zheng Dan, Zhang Shaokun, Li Lei, et al. Research on switching losses testing method for SiC MOSFET[J]. Proceedings of the CSEE, 2020, 40(9): 2975-2983.

Suppression of Voltage Spike in Resonant Switched Capacitor Converter Considering Parasitic Inductance

11121,34

（1. School of Electrical Engineering Beijing Jiaotong University Beijing 100044 China 2. Electric Power Research Institute State Grid Zhejiang Electric Power Co. Ltd Hangzhou 310014 China 3. Key Laboratory of Optical Engineering Chinese Academy of Sciences Chengdu 610209 China 4. Fuji Electric Co. Ltd Tokyo 141-0032 Japan）

The resonant switched capacitor converter (RSCC) based on silicon carbide (SiC) devices is suitable for high operation efficiency and power density due to its soft switching characteristics. However, the high operation frequency makes it sensitive to the parasitic inductance, which may cause the voltage spike of switching devices. By analyzing the RSCC laminated busbar model, the equivalent circuit with parasitic inductance was built. The influence of parasitic inductance on the operating mode of the circuit was studied, and the relationship between the parasitic inductance and the voltage spike of the switching devices was derived. Accordingly, this paper proposed two voltage spike suppression methods for optimizing the laminated busbar model and the snubber capacitance. Simulation and experimental results verified the effectiveness and feasibility of the voltage spike suppression methods in this paper.

Resonant switched capacitor converter, laminated busbar, parasitic inductance, voltage spike suppression

TM46

10.19595/j.cnki.1000-6753.tces.L90231

国网浙江省电力有限公司科技项目（5211DS19003A）和国家自然科学基金重点项目（51737001）资助。

2020-07-04

2020-11-09

刘 妍 女，1998年生，硕士研究生，研究方向为大功率电力电子变换器及其控制。E-mail: 19121461@bjtu.edu.cn

杨晓峰 男，1980年生，副教授，博士生导师，研究方向为多电平变换器技术、柔性直流输电技术、电力电子技术在轨道交通中的应用。E-mail: xfyang@bjtu.edu.cn（通信作者）

（编辑 陈 诚）