胶体聚合物弹性模量的微观理论: 键长的效应*

张博凯

(浙江理工大学物理系, 杭州 310018)

1 引 言

玻璃材料弹性性质的刻画是凝聚态物理、统计物理和材料物理中广泛关注的问题[1-3].从结构上看, 玻璃材料保持着无序的类似液体的静态结构,但在动力学和流变学上却展现出固体特有的性质,如发散的弛豫时间和非零的弹性模量[4].建立一个基于系统微观的静态结构, 预测宏观慢动力学和流变学性质的理论框架是玻璃物理中长期的理论难点.在实际应用中, 从微观上理解材料相关的参数对宏观的动力学和力学性质的影响, 能为玻璃的化学合成和工业运用提供定性定量的指导.

本文关注高密度下胶体聚合物体系弹性模量的理论预测.2010年以来, 国内外很多研究组在实验上将胶体粒子作为基本单元, 用以合成链状的胶体聚合物分子[5-7].近年来, 胶体聚合物因兼具聚合物链连接性和胶体单元的可视性, 而成为了探测和理解聚合物玻璃的重要材料.具体表现在: 1) 胶体粒子的尺寸分布为10 nm—0 μm, 这使得它们更容易被光学显微镜观测到[8]; 2) 相对于分子聚合物玻璃, 胶体聚合物的链段单元是清晰的, 即每一个胶体粒子单元就是一个链段; 3) 胶体聚合物材料能方便地控制分子的微观参数(链长、键长和结构单元的形状), 使其成为研究聚合物玻璃性质的理想模型.

模耦合理论是刻画液体玻璃化转变中普遍而有效的微观理论[9,10].其主要的思想是利用投影算子技术将与玻璃动力学无关的快变量预先积分掉,得到一个关于慢变量的动力学方程.该方程能够预测外部参数变化后各态历经-非各态历经转变, 但其并不能处理玻璃化转变点以下的动力学.为此,Schweizer和Saltzman[11,12]提出了非线性朗之万方程理论, 该理论结合液体的密度泛函理论推广了模耦合理论, 使其能够处理深过冷态下粒子的激发跳跃过程.这一理论进展使得微观上研究玻璃材料的弛豫和流变学性质成为可能[13-15].在上述的微观理论中, 主要包含两个部分内容: 1) 使用积分方程理论计算系统的静态结构; 2) 将静态结构代入动力学方程中预测其动力学和流变性质.

在胶体聚合物中, 用于预测静态结构的积分方程理论主要是高分子参考作用点模型 (polymer reference interaction site model, PRISM)[16].PRISM积分方程理论能够计算实空间和傅里叶空间的静态结构, 并在定性和定量上与散射实验很好的符合.最近, PRISM理论框架被推广应用于诸多聚合物体系, 如高斯链模型[17,18]、聚合物-纳米粒子复合物[19,20]和环状聚合物[21,22].结构信息的研究联系着系统的黏弹性行为、热力学、微观有效相互作用以及宏观相行为[23-25].

动力学方面, 微观的非线性朗之万方程理论用于计算过冷液体中示踪粒子的慢动力学性质[11,26].该理论引入动力学自由能的概念, 预测了玻璃化转变点、α弛豫时间和局域尺寸.近年来, 该理论被成功地推广并在诸多体系取得了长足的发展, 刻画了如聚合物纳米复合物[27]、环形聚合物[21]以及胶体聚合物[28]在过冷区域内的各种慢动力学行为.

在我们以前的工作中, 将胶体聚合物建模成离散的蠕虫链模型[29].该模型包含了胶体聚合物的体积分数、链长、键长以及链内局部弯曲能.该模型使得我们可以研究胶体聚合物键长对系统相关慢动力学量的影响, 如α弛豫、势垒高度和局域尺寸[28].我们发现了键长对相关动力学量的独特作用: 对于同一键长的胶体聚合物体系, 如果使用过冷深度φc-φ作为自变量, 上述慢动力学量能塌缩到同一普适曲线上, 而不依赖于链长和局部弯曲能.

本文将关注高密度状态下胶体聚合物的弹性,重点关注键长在胶体聚合物的弹性影响因素中的角色.基于剪切弹性模量微观的Green-Kubo关系, 利用模耦合理论推导了胶体聚合物系统的剪切弹性模量的表达式.该表达式依赖于系统的静态结构因子及单个胶体粒子的局域尺寸.基于静态结构分析, 研究了不同键长、不同弯曲能下系统的剪切弹性模量.最后也报道了相关链参数对体积弹性模量的影响.重点探讨了剪切和体积弹性模量-体积分数曲线在不同键长下的行为.

2 结构与动力学计算方法

2.1 PRISM理论

首先, PRISM理论将聚合物中的单体假设为一系列位点所组成的系统[16].如图1所示的聚合物系统, 系统静态的结构由两个单体a和b的总关联函数、单链结构因子和直接关联函数刻画.它们之间的关系由Ornstein-Zernike方程描述[30]:

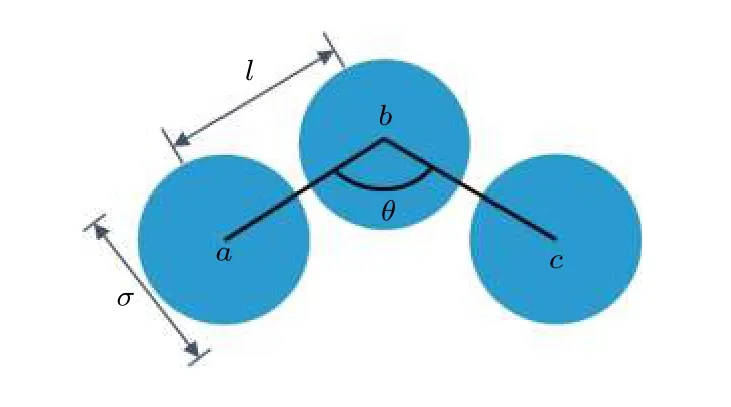
图1 胶体聚合物模型的示意图, 包含了模型中3个连续单体(蓝球)和关键的尺度(半径和键长)与键角Fig.1.Schematic of colloidal polymers.Blue spheres represent three consecutive monomers with diameter σ , bond angle θ and bond length l.

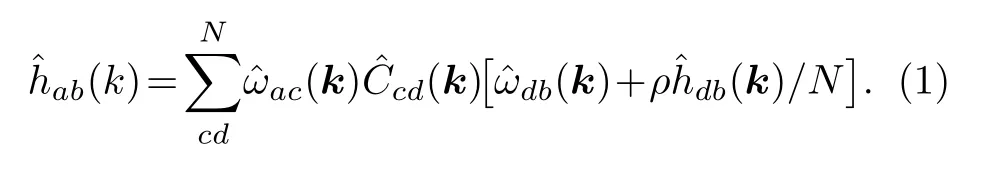
这里ρ是单体的数密度,N是一个聚合物分子中单体的数目,N是波矢, 角标代表系统中聚合物单体的编号.(1)式右边第一项代表链内相互作用与链间直接相互作用耦合的贡献, 第二项代表其他单体作为中间介导物而产生的间接多体关联.针对不同的聚合物模型(如高斯线模型、自由连接链模型和蠕虫链模型), 链内的关联函数是已知的.将其作为已知的输入函数, 要求解(1)式, 则需要额外的联系着和的封闭近似方程, 即可迭代求解聚合物系统的静态结构和.本文中假设胶体聚合物单体间的相互作用是硬球排斥势,所以采用经典的Percus-Yevick封闭, 其在实空间表达为

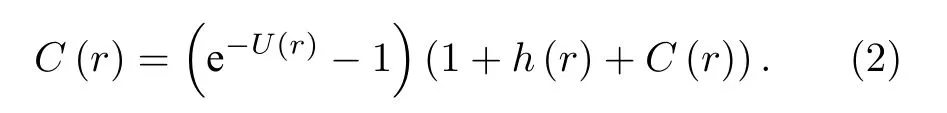
这里U(r) 为系统中两个单体直接的相互作用势,C(r) 代表单体间直接关联函数, 而h(r) 是单体间总的多体关联函数.

2.2 胶体聚合物模型

我们采用离散的蠕虫链模型对胶体聚合物进行建模[29].该模型包含了单体之间的体积排斥作用、链的连接性以及链内局部的刚性.在实空间中,该模型将同一条链中两个单体a和b的分布函数表示为

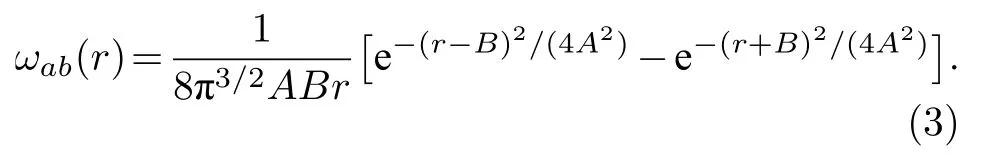
这里r是两个单体直接的距离, 系数A和B是单体分布矩的函数.这些分布矩依赖于键长l,其中〈·〉代表在链内局部弯曲能下对不同角度分布的平均,

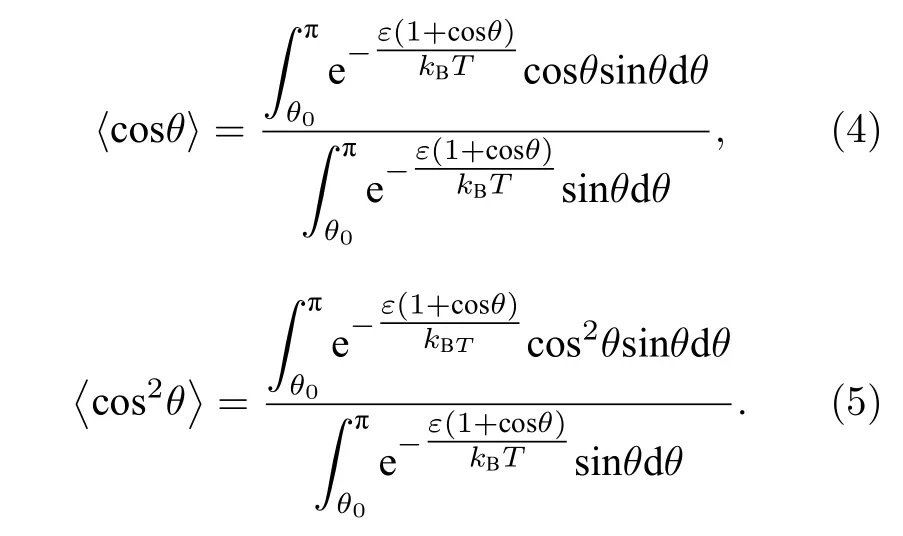
由于排斥体积相互作用, c osθ0=1-σ2/l2,σ是每个单体的直径.推导的细节和具体的表达式见文献[29].通过得到了平均后的实空间单链关联函数.在本文中, 主要报道N=10的数据.

2.3 非线性朗之万方程理论和弹性模量的微观表达

非线性朗之万方程理论刻画每个单体在周围粒子形成的笼效应的短时局域运动和长时激发跳跃过程.对每个示踪粒子, 其时间相关的位移rs(t) ,满足非线性朗之万方程:

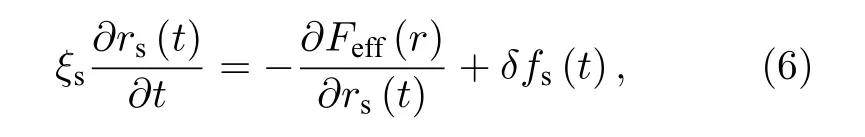
其 中ξs是溶液 的 摩 擦 系数,δfs(t) 是 高斯白噪声.对于聚合物体系, 考虑其内部的连接性和链内关联, 推导出动力学自由能Feff的表达式为[28]

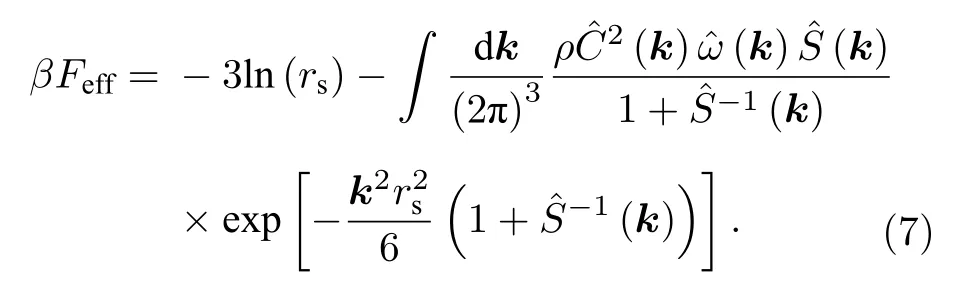
这里忽略了链内的直接关联,β=1/kBT.动力学自由能预测了玻璃化转变的局域尺寸和激发势垒高度.在外部参数(体积分数、温度)变化下, 液体对应动力学自由能随着示踪粒子位置rs单调下降,而过冷液体对应着自由能曲线开始出现极小值, 理论上定义此为过冷液体转变点, 极小值对应的示踪粒子的位置是局域尺寸rloc.随着过冷程度的加深,势垒高度越深, 相应的局域位置越小.

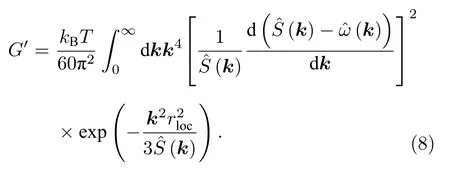
在链状分子中,ωˆ 的减去预示分子内部的应力对整个弹性模量是不重要的.根据上述表达式, 剪切弹性模量依赖于相关玻璃材料的静态结构的信息和局域尺寸.

对于体积弹性模量, 其联系着系统整体的热力学量, 定义为KB=ρ(∂P/∂ρ)T.在液体理论中, 此物理量联系着系统长波长的密度涨落, 表达为[30]

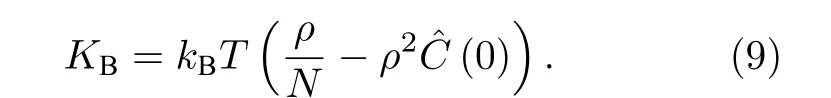
在本文中, 长度单位取为单体的直径σ, 弯曲能的单位为kBT, 弹性模量的单位为kBT/σ-3.

3 计算结果与讨论

首先, 研究了离散的蠕虫链的单链结构因子ω(k), 重点关注键长在不同波矢下对单链结构因子的影响.如图2(a)所示, 单链结构因子ω(k) 在波矢k→0 趋近于链的单体数目N, 在k→+∞时, 振荡衰减到0.数据显示: 在不同键长下, 在k＜1区域内, 单链结构因子几乎没有差别.在中间波矢区域, 即k=1—10 , 不同键长的单链结构因子开始展现出差异.具体地, 键长越大, 在此区域内,归一化的单链结构因子具有更大的数值.更定量地, 在这个区域, 本文计算结果展示单链结构因子满足幂律衰减ω(k)～k-μ且μ≈2 , 这个衰减指数不依赖于键长.以往的模拟和理论都揭示了衰减指数μ反映了不同的拓扑结构的分子, 如硬棒分子(μ=1 )、环性聚合物(μ=3 )和线性柔性分子(μ=2 )[32].

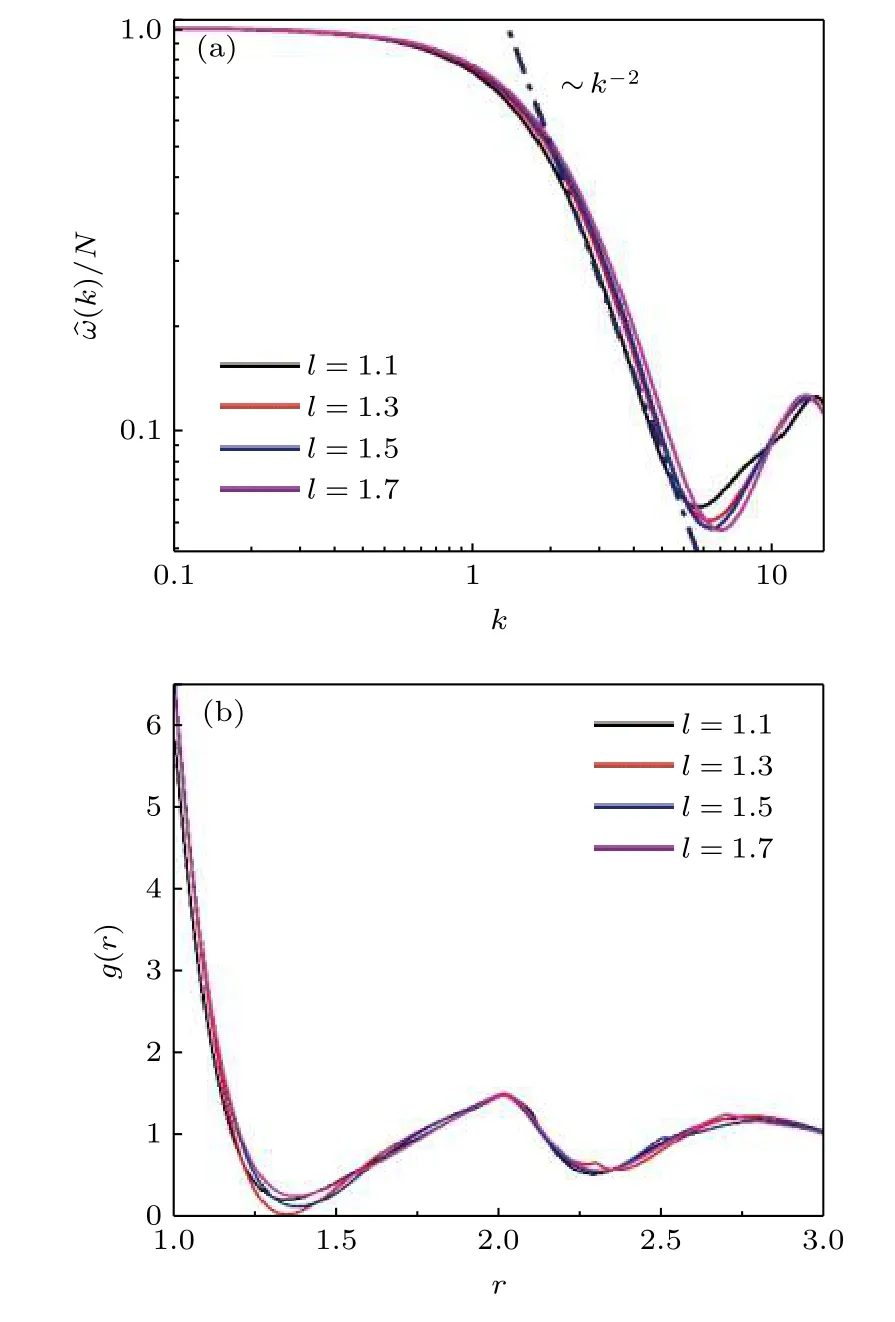
图2 静态结构 (a) 在不同键长下的单链结构因子, 虚点线显示在中级波矢范围满足幂律衰减 ～ k-2 ; (b) 不同键长下的径向分布函数Fig.2.Static Structure functions: (a) Intrachain structure factor for different bond lengths (dashed-dotted line shows a power law decay ～ k-2 at intermediate wavevector); (b) the radial distribution functions for different bond lengths.

图2 (b)进一步展示了不同键长下单体分布的径向分布函数g(r) , 可以看出, 键长主要影响r≈1.25σ—1.3σ区域内, 这个位置对应了径向分布函数极小的位置, 即单体第一壳层的位置.因此, 理论计算猜想键长对于结构的影响主要在第一壳层粒子的分布, 该分布对应着示踪粒子的临近粒子的分布, 从而改变了由周围粒子形成的笼效应.

将上述计算的静态结构代入动力学自由能(7)式, 关注键长对于过冷液体转变的临界体积分数φc的影响.图3展示了在不同链内弯曲能ε下,φc-l的关系: 临界体积分数随着键长增加而单调的下降, 并在l≥1.5σ处趋于饱和.这意味着键长增加使得系统的玻璃化转变更容易了.φc饱和的位置弱依赖于链内弯曲能.当弯曲能由ε=0—1.0 时,φc≈0.43—0.422.图3中虚线显示出硬球的临界转变体积分数=0.432.在l≥1.5σ时, 柔性的胶体聚合物(ε=0 )的转变点更接近于.

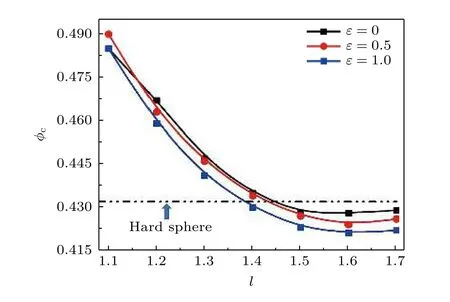
图3 不同链内弯曲能下, 玻璃化转变体积分数随着链长的变化Fig.3.Crossover volume fraction as a function of bond length for different bending energies.

在(8)式中, 剪切弹性模量依赖于局域尺寸和静态结构, 因此首先报道键长对局域尺寸的影响.在以往的工作中[28], 我们已经发现: 只要将过冷深度φ-φc作为自变量, 局域尺寸和动力学自由能势垒均能坍缩到一条普适的曲线上, 而并不依赖于链的单体数目和链内的弯曲自由能.如图4(a)所示,展示了3个不同键长下3个不同链内弯曲能的局域尺寸的数据.局域尺寸随着过冷深度而单调下降, 并在大的过冷深度参数下, 满足指数衰减rloc～e-α(φ-φc).随着键长的增加, 这个指数上系数α的变化范围为α=20.056—13.247 , 在大的键长下, 接近于硬球的结果α=14.658 (图4(a)中的绿色实线).

将得到的局域尺寸和静态结构代入(8)式中,计算了不同过冷深度的剪切弹性模量.如图4(b)所示, 发现剪切弹性模量随着过冷深度的增加而迅速增加, 从G′≈20 到G′≈3000 , 增加了大约两个数量级.并且在大的过冷深度下, 以指数的形式增加,G′～eβ(φ-φc).当l=1.1 时, 柔性聚合物(ε=0 )在大的过冷深度下满足G′～e27.027(φ-φc), 而l=1.7 时,G′～e25.707(φ-φc).对于硬球系统,G′～e26.581(φ-φc),发现其指数β变化不大.但与局域尺寸不同的是,虽然对于同一个键长, 不同的链内弯曲能的剪切弹性模量数据更接近, 但是我们的理论揭示: 它们并不能坍缩到一条普适的指数增长曲线上.

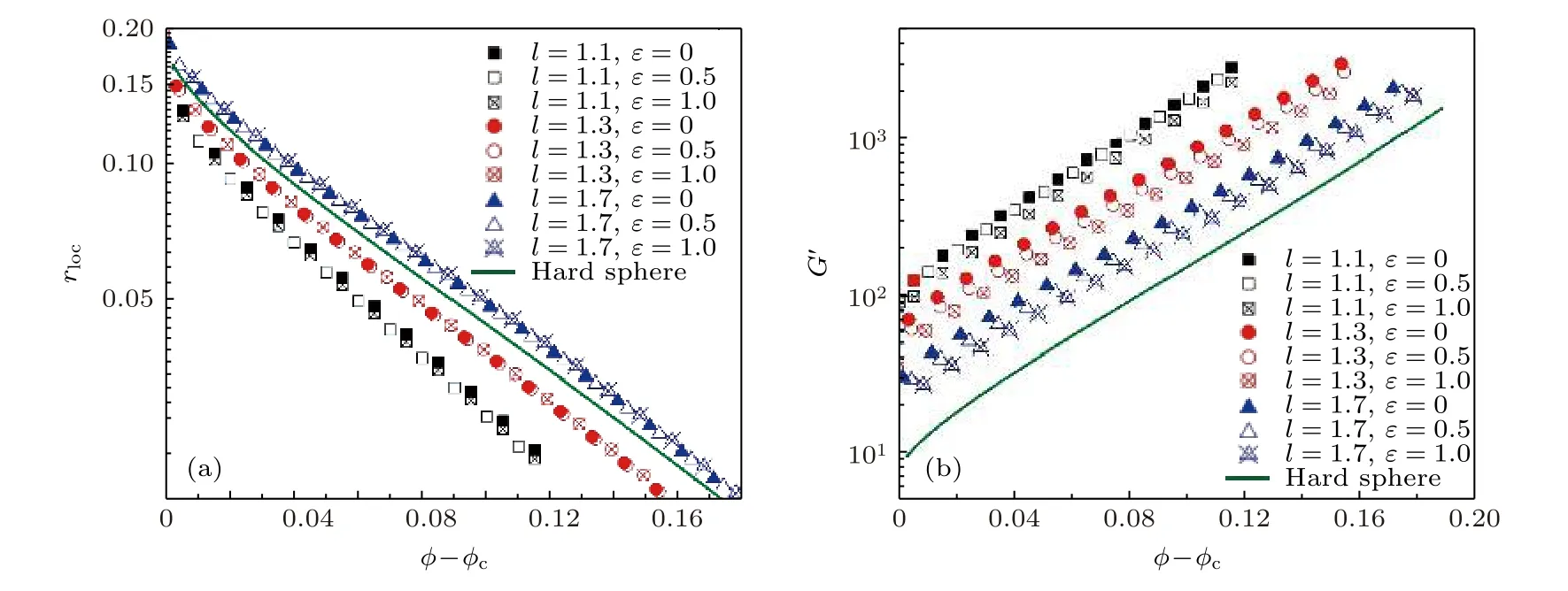
图4 (a) 不同链内弯曲能和键长的局域尺寸随着玻璃化深度的变化, 绿线是硬球液体的局域尺寸; (b) 不同链内弯曲能和键长的剪切弹性模量随着玻璃化深度 φ -φc 的变化, 绿线是硬球的数据Fig.4.(a) Localization length as a function of φ -φc for different bending energies and bond lengths.Green line represents localization length for hard sphere liquids.(b) shear modulus as a function of φ -φc for different bending energies and bond lengths.Green line represents shear modulus for hard sphere liquids.

我们转而研究体积弹性模量.将长波长的直接关联函数代入(9)式进行计算, 图5(a)显示了不同键长下不同的链内弯曲能对胶体聚合物系统的体积弹性模量的影响.研究发现体积弹性模量随着过冷深度迅速地增加,KB≈20—200 , 约一个数量级.在本文理论研究的整个范围内, 体积弹性模量的数据都展示出其随着过冷深度而发生指数增长的趋势, 在长键长下(l=1.7σ),KB～e13.821(φ-φc), 接近于硬球的体积弹性模量的行为:KB～e13.768(φ-φc).有趣的是, 和局域尺寸一样, 体积弹性模量-过冷深度曲线也展现出独特的键长依赖关系: 同一键长而不同链内弯曲能的KB(φ-φc) 曲线坍缩到一条普适的指数增长曲线.

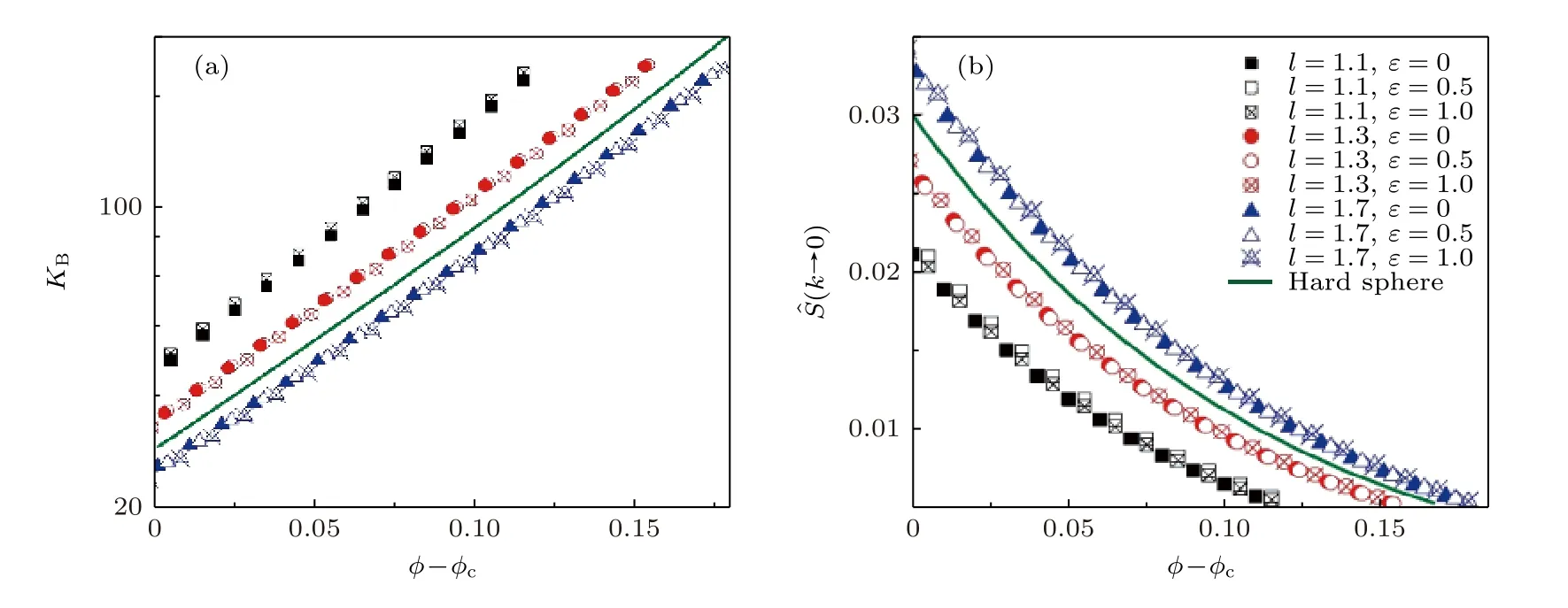
图5 (a) 不同链内弯曲能和键长下, 体积弹性模量随着玻璃化转变深度的变化.绿色线代表硬球液体的体积弹性模量.(a)和(b)的图例是一致的.(b) 不同链内弯曲能和键长下, 静态结构因子的零波矢数值随着玻璃化转变深度的变化.Fig.5.(a) Bulk modulus as a function of φ -φc for different bending energies and bond lengths.Green line represents bulk modulus for hard sphere liquid.The legend is the same as in panel (b).(b) Static structure factor at zero wavevector for different bending energies and bond lengths.Green line represents corresponding data for hard sphere liquid.

为解释本文发现的键长对于体积弹性模量的普适曲线的调控行为, 我们猜想这主要来自于键长对静态结构因子中零波矢((k→0) )附近行为的调控.在液体理论中, 零波矢(长波长)的密度涨落直接联系这系统的宏观热力学变量, 进而影响系统的体积弹性模量.为此, 图5(b)展示了零波矢结构因子和过冷深度之间的关系.有趣的是, 对于同一个键长, 无论其内部弯曲能如何,(k→0) 始终能够塌缩到同一条普适曲线上.这一发现说明了弹性模量的普适曲线实际上是来自于零波矢结构因子的普适曲线.

4 总结与讨论

本文利用模耦合理论中的投影算子技术, 在胶体聚合物静态结构和局域尺寸的基础上, 在过冷液体动力学自由能的概念下, 结合过冷液体激发跳跃的物理图像, 推导了弹性剪切模量的显式表达.在胶体聚合物体系中, 利用此理论探索键长在弹性模量影响因素中的特殊角色.在计算结果中, 首先关注了键长在静态结构上的影响, 进而发现调节键长会使得系统更容易玻璃化转变, 即过冷液体临界转变体积分数降低.随后发现了剪切弹性模量随着过冷深度参数的指数增长行为, 但对于同一键长,G′(φ-φc)曲线并没有坍缩到一条普适曲线上,而体积弹性模量—只依赖于零波矢附近的静态结构, 则展现出了相应的普适曲线.零波矢静态结构因子展现出的普适行为使得我们猜想: 弹性模量的普适曲线实际上是来自于键长对特定波矢的结构因子的普适性.在剪切弹性模量的表达式(8)中,其具体数值来自于对整个波矢空间中静态结构函数的积分.因此,G′(φ-φc) 曲线对于普适曲线的偏离是来自于键长对长波矢的结构因子的影响.在将来的研究中, 本工作可以推广到有外加剪切形变和蠕动的情形, 从而更清晰地理解键长对胶体聚合物流变学的作用.