具有时变时滞的线性离散随机系统的间歇故障检测

张 森,盛 立,高 明

(中国石油大学(华东)控制科学与工程学院,山东青岛 266580)

1 引言

随着控制理论与计算机技术的发展,现代工业技术装备和自动化控制系统变得更加复杂化,高效化和智能化.众所周知,故障诊断技术是一种提高动态系统安全性和可靠性的有效方法[1].在故障诊断技术领域,与硬件冗余技术相比,基于模型的故障诊断方法由于其具有耗费低,性能好和应用范围广等优势,已逐渐成为故障诊断研究领域的重要手段,并且已有大量相关研究成果[2-5].

在工业系统中,由于设备的老化和工作环境的复杂化,难免会产生各种类型的故障,其中一种常见的故障被人们称为间歇故障[6].例如,在电力系统中,电线的磨损老化会产生间歇的电弧,如果不及时处理,最终可能会演变成间歇电弧故障[7].在航空飞行领域中,大约超过一半的电子设备故障为间歇故障[8].通常来说,间歇故障具有随机消失,随机出现的特性,而且它的活跃时间和间隔时间都不确定,这就对间歇故障的检测带来极大的困难.考虑到间歇故障的随机特性,间歇故障检测不仅要求检测出故障的发生时刻,还要求检测出故障的消失时刻,这也是间歇故障检测的难点所在.

最近几年,间歇故障的检测逐渐吸引了众多学者的研究兴趣[9-10].例如,文献[11]研究了一类离散事件系统传感器间歇故障的可检测性问题.文献[12]研究了具有输出死区的离散线性随机系统的间歇故障诊断问题.文献[13]在假设间歇故障发生概率先验已知的情况下,研究了一类具有非均匀采样与动态量化的网络化多速率系统的间歇故障检测问题.最近,基于最小化估计误差协方差法,文献[14-16]研究了线性时变系统的间歇故障检测问题.然而上述文献对间歇故障的可检测性,漏报率和误报率均没有进行适当的分析.在文献[17-20]中,创新性的设计了两个假设检验分别对间歇故障的发生时刻和消失时刻进行检测,并且在残差统计特性分析的框架下研究了间歇故障的可检测性、漏报率和误报率等问题.但截至目前,间歇故障检测对象模型大多是非时滞系统,针对时滞系统间歇故障诊断的研究鲜有报道.

实际上,由于信号传递需要一定的时间,工业生产过程中的系统几乎都存在时间延迟的特性[21].因此,研究时滞系统故障检测问题具有非常重要的现实意义,并且在相关研究领域已有众多研究成果.文献[22]为状态时滞动态系统设计了一种未知输入观测器来对故障进行检测.文献[23]采用了三角算子和输入输出方法来检测T-S模糊时滞系统的故障.在文献[24]中,研究了一种基于功能观测器的时滞系统故障检测方法.最近,文献[25]研究了一类基于分布式功能观测器的互联时滞系统故障检测问题.然而,上述文献的故障检测问题只考虑到对故障发生时刻的检测,研究间歇故障消失时刻检测问题的较少.文献[26]基于滑动窗口方法对一类具有定常时滞的线性随机系统的间歇故障检测问题研究进行了初步的探索,但在时变时滞的情况下该方法不再适用.因此,研究具有时变时滞系统的间歇故障检测问题具有重要的理论意义与应用价值.

本文针对一类具有未知扰动的线性离散时变时滞系统,在其时变时滞满足周期性变化规律的前提下,研究了其间歇故障检测问题.论文主要创新点包括:1)研究了线性离散时变时滞系统的间歇故障检测问题;2)结合等价空间法,利用两个假设检验来分别检测间歇故障的发生时刻和消失时刻;3)在残差统计特性分析的框架下,分析了间歇故障的可检测性.

2 问题描述

考虑一类存在未知扰动的线性离散时变时滞系统:

其中:符号mod(k,T)表示求余运算,l表示最大时滞步数.从h(k)的表达式中可以看出,此类时变时滞具有周期性变化的规律,为了简化符号表示,令周期T=l+1.

在模型(1)中,f(k)∈R代表间歇故障.在实际应用中,间歇故障可以被描述为一系列可以重复出现的突变,且这些突变的活跃时间和间隔时间具有一定的不确定性.随着时间的推移,间歇故障的活跃时间会变得更长,间隔时间会变得更短,最终会演化为永久故障.基于以上间歇故障的特点,本文研究的间歇故障模型描述为下式:

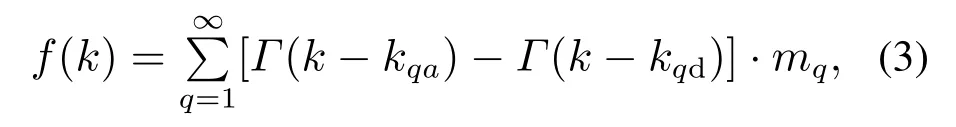
其中:Γ(·)为离散阶跃函数,kqa和kqd分别表示间歇故障的第q次故障的发生时刻和消失时刻,mq表示第q次间歇故障的幅值.由于间歇故障具有随机的活跃时间和间隔时间,定义第q次间歇故障的活跃时间为,间隔时间为本文对于以上的离散时变时滞系统和间歇故障模型,做出如下假设:

假设1线性离散时变时滞系统(1)完全可观测且其输出维数大于扰动维数,即ny＞nd.

假设2i)间歇故障的幅值存在一个已知的最小值λ,即所有的间歇故障幅值都满足|mq|≥λ;ii)间歇故障的最小活跃时间和最小间隔时间都是先验已知的;iii)定义τmin=min,且τmin

注1假设2是根据实际操作经验和历史记录数据提出的,即间歇故障往往具有有限的活跃时间和间隔时间.此外,较小的间歇故障对系统的正常运行不会造成影响.因此,本文提出的待检测间歇故障模型具有最小幅值,最小活跃时间和最小间隔时间是合理的.

对于系统(1)所描述的具有未知扰动的线性离散时变时滞系统,令

由文献[27]可知,线性离散周期系统(4)可以利用提升技术转化成线性离散时不变系统,设τ ∈[0,T-1]且τ ∈N,对状态方程利用叠加原理可得

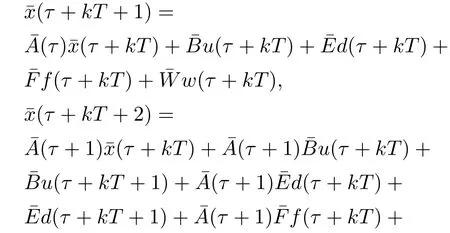
3 时变时滞间歇故障检测方法

间歇故障的检测不仅要求在故障消失之前检测到发生时刻,而且要求在下一个故障发生之前检测到当前故障的消失时刻.针对间歇故障的特性和检测要求,本节设计了对外部未知扰动解耦的标量鲁棒残差.在考虑随机噪声影响的同时,利用两个假设检验分别检测间歇故障的发生时刻和消失时刻,并分析了间歇故障的可诊断性问题.

3.1 鲁棒残差设计

针对系统(8),为了能够设计残差使其对外部未知扰动解耦,并且对间歇故障敏感,采用等价空间法,通过选择合适的滑动时间窗口s来构建鲁棒残差,对于任意的滑动时间窗口s ＞0,有

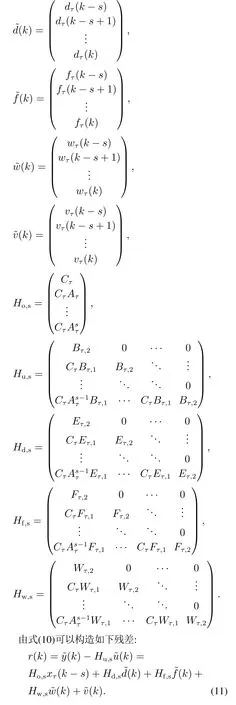
在式(11)中,根据等价空间法,设计的鲁棒残差需要对初始状态xτ(k-s)和外部未知扰动解耦,同时还要对待测间歇故障敏感.注意到间歇故障的最小活跃时间和最小间隔时间是先验已知的,根据文献[28],选择滑动时间窗口使其满足以下条件:

从式(12)中可以看出,鲁棒残差只与间歇故障,过程噪声和测量噪声有关.为了方便分析鲁棒残差的统计特性,设计一个结构化标量残差如下式所示:

其中Λ为具有适当维数的标量残差生成列向量.

3.2 间歇故障检测

间歇故障检测要求在间歇故障消失之前检测到故障发生时刻,在下一次故障发生之前能够检测到故障的消失时刻.为了准确的设定检测阈值,首先要对鲁棒残差的统计特性进行分析,由式(13)可知,结构化标量残差可以被重写为

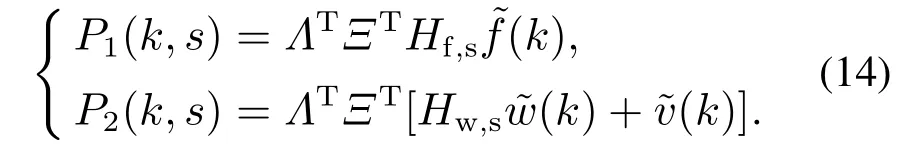
由于w(k)和v(k)是相互独立的零均值高斯白噪声,那么(k)和(k)也是相互独立的零均值高斯白噪声,且其方差分别为和.那么P2(k,Δk)也是服从高斯分布的,其均值为零,方差为

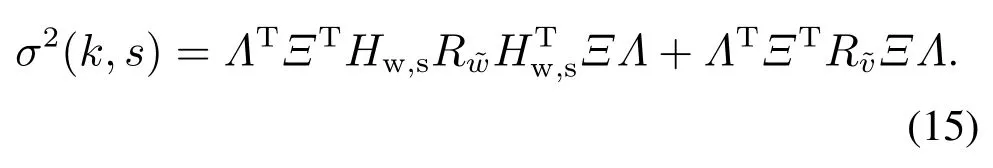
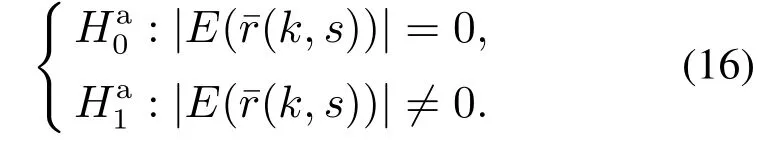
对于给定的显著性水平γ,可以得到发生时刻的检测接受域为

当滑动时间窗口完全位于间歇故障内时,根据假设2可知,一个间歇故障的幅值具有最小值λ.定义一个元素全为1的列向量1f ∈R(l+1)(s+1)×1,则

根据文献[17],间歇故障的消失时刻可以被以下的假设检验来检测:

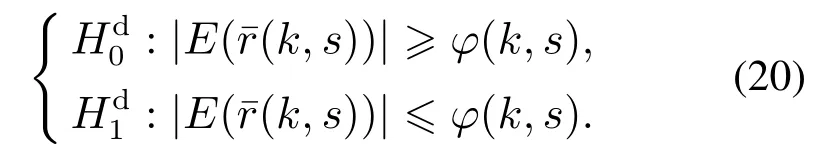
对于给定的显著性水平ϑ,可以得到消失时刻的检测接受域为

这里的Hϑ表示标准正态分布变量具有ϑ的概率落在(Hϑ,+∞)内.

因此,对于给定的滑动时间窗口s和显著性水平γ,间歇故障消失时刻的检测阈值θd为

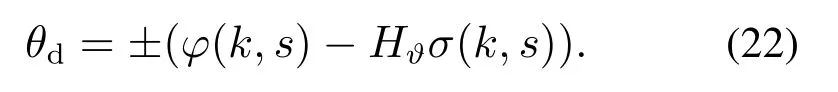
3.3 间歇故障可诊断性分析

由第3.2节可知,间歇故障检测要求当前故障的发生时刻要在当前故障消失之前检测到,在下一个间歇故障出现之前,当前故障的消失时刻要检测完毕.因此,对于给定的滑动时间窗口s,间歇故障发生时刻和消失时刻能够准确检测到的充分条件为W(k,s)∩V(k,s)=∅.本文采用了两个假设检验来分别检测间歇故障的发生时刻和消失时刻,这就导致了两个假设检验的接受域存在交集的情况,从而影响间歇故障的检测,因此定义

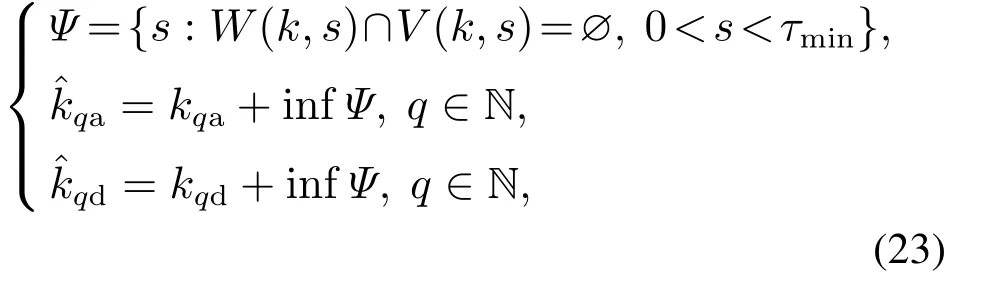
这里的Ψ是在间歇故障可检测框架下滑动时间窗口s的集合,当滑动时间窗口s给定以后,也就确定了间歇故障实际检测值与真实值之间的最大延迟,也就是说,间歇故障发生时刻kqa的最佳测量值为.同理,间歇故障消失时刻kqd的最佳测量值为,给出间歇故障可检测性定义如下:

证此定理的证明可以通过以下步骤得到:

步骤1首先,由于间歇故障的发生时刻和消失时刻分别是通过两个假设检验来检测得到的.因此,通过式(17)和式(21)得到的两个接受域交集应为空集,即W(k,s)∩V(k,s)=∅.

4 仿真验证

为了验证上述方法的有效性,本节在一个简化的无人飞行控制系统模型[19,29]上进行了仿真验证.该飞行控制系统受到未知扰动的离散系统模型为

其中:x(k)=(η(k)(k)δ(k))T;η(k)为正常飞行速度(kts);(k)为俯仰角速度((°)/s);δ(k)为俯仰角();u(k)为升降舵控制信号;d(k)为电子信号干扰;f(k)为发生在舵机上的间歇故障信号;w(k)为复杂飞行环境引起的过程噪声;v(k)为测量噪声.假设w(k)和v(k)都是已知的零均值的高斯白噪声,其方差分别为Rw和Rv.系统(27)中其他矩阵参数分别为

为保证无人机跟踪预设运行轨迹的性能,仿真采用状态反馈控制律u=-Kx(k),其中

仿真中的间歇故障模型如图1所示,其最小活跃时间=10,最小间隔时间=10,间歇故障的最小幅值λ=0.8.假设最大时滞步数l=1,从式(11)和式(12)中,可以得到满足对外部未知扰动解耦且对故障敏感的最小值s=2,容易验证rank(Ho,sHd,sHf,s)=6 且rank(Ho,sHd,s)=8.因此,可以建立一个鲁棒残差使得其对外部未知扰动解耦并且对间歇故障敏感.选取两个假设检验的显著性水平分别为γ=0.05和ϑ=0.05,可以得到间歇故障发生时刻和消失时刻的检测阈值分别为θa=±0.1328和θb=±0.1204.

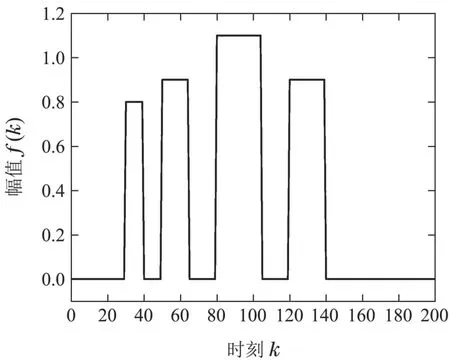
图1 间歇故障Fig.1 The intermittent fault

本文建立标量鲁棒残差对间歇故障进行实时检测的效果如图2所示,当间歇故障没有发生时,标量残差¯r(k,s)只在平衡点附近的很小的范围内波动,说明设计的结构化鲁棒残差能够实现对外部未知扰动解耦;当间歇故障发生后,残差¯r(k,s)以较快的速度超越检测阈值θa,及时的检测出间歇故障的发生时刻.当间歇故障消失后,残差¯r(k,s)仍能以较快的速度超越检测阈值θd,及时的检测得到间歇故障的消失时刻.由图3可以看出,所有的间歇故障发生时刻都能在间歇故障消失前准确检测得到,所有的间歇故障消失时刻都能在下一个间歇故障发生前被检测得到,检测结果表明,该方法能够准确检测到间歇故障所有的发生时刻和消失时刻.

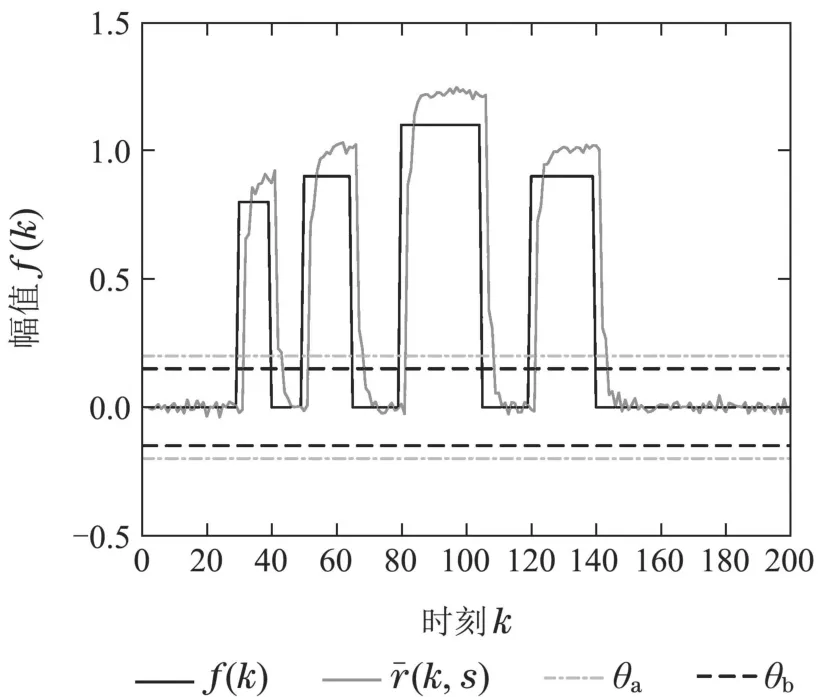
图2 标量残差Fig.2 The scalar residual

为了更好的说明所述方法的有效性,对于上述问题,本仿真采用传统龙伯格观测器的方法进行对比实验.基于龙伯格观测器方法所建立的残差如图4所示,当间歇故障发生后,第一个故障的发生时刻能够很快的被检测到.在故障消失后,由于前一时刻的故障影响还存在与当前的误差中,所以残差无法快速的降到阈值以下,无法检测到当前故障的消失时刻,进而会影响后续间歇故障的检测,无法给出准确的测量结果.因此,与传统龙伯格观测器方法相比,本文提出的间歇故障诊断方法能够更为有效的检测间歇故障.

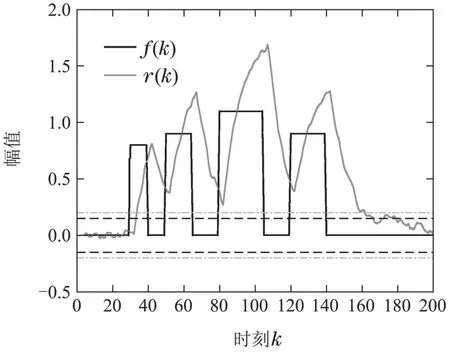
图4 基于龙伯格观测器得到的残差Fig.4 The residual derived from Luenberger observer

5 结论

论文针对一类存在未知扰动的线性时变时滞离散随机系统的间歇故障检测问题,提出一种鲁棒间歇故障的检测方法.基于提升技术和叠加原理,首先将时变时滞系统转化为时不变系统.在等价空间法的基础上,通过引入滑动时间窗口,设计了一个对外部未知扰动解耦且对间歇故障敏感的结构化鲁棒标量残差,该残差对间歇故障的发生和消失更加的敏感.在给定显著性水平的前提下,利用两个假设检验来分别检测间歇故障的发生时刻和消失时刻.最后,通过一个无人机仿真实验验证了此方法的有效性.