基于神经网络的高精度守时算法研究
2021-07-01苗自云于兆磊朱智林
苗自云,于兆磊,朱智林
(1.山东工商学院,山东 烟台 264003;2.烟台恩邦电子科技有限公司,山东 烟台 264006)
0 引 言
高精密时间频率系统是现代化战争中实现精确打击的基础,而守时工作是精密时间频率系统的基础和核心内容[1]。频率标准源作为时间频率系统的守时设备,为一些设备提供标准频率信号。考虑到野外作战的特殊环境,需要适应更宽的工作温度范围,也要求频率标准源具有较高的精度和准确度。目前,具有高准确度的频标主要有原子钟和晶体振荡器,原子钟的频率准确度较晶体振荡器更高,但其使用环境要求较高,且价格昂贵。晶体振荡器的价格相对便宜,且使用寿命长,应用广泛,但其精度易受温度、老化等因素影响,长期稳定性差,只能满足普通需求[2-3]。
GPS信号是具有原子频率标准的标准源,具有较高的精度和准确度,因此利用GPS接收机接收GPS信号后对地面晶体振荡器进行校准,可以获得精度较高的频率标准源。GPS信号容易受到复杂气象条件的制约与地理环境的影响,这时晶体振荡器只能依靠自身实现高精度频率输出[4]。要实现高精度的频率输出就需要对晶振的频率漂移量进行补偿。
频率漂移的补偿关键在于利用历史频偏数据合理建模预测下一阶段的频偏。受制造工艺影响,晶振个体之间会存在物理结构的差异,即使是同一切型、同一切角的石英晶体在相同工作时间、相同的环境中也会产生不同的频偏,而且晶振频率也会受到温度、老化等因素的影响,因此难以从原理上分析出晶振频偏的规律,并用数学公式推导得到准确描述[5-6]。传统的预测方法中通常采用最小二乘拟合模型或者经验模型进行预测,最小二乘拟合模型或经验模型需要事先确定样本的多项式次数,再利用历史数据拟合得到各次项的系数作外推计算下一时刻的频偏。这种方法的自适应能力较差,预测精度较低。本文提供了一种基于神经网络的频率预测算法,经过系统训练和学习,能够快速找出输入参数和输出参数之间的内在联系,进行非线性预测,适合本文对频率漂移量的预测。适用于非线性预测的人工神经网络目前主要有RBF神经网络和BP神经网络等。李依泽[5]等利用BP神经网络对恒温晶振因老化因素引起的频偏进行预测;高宝玲[6]等利用BP神经网络设计温度补偿晶体振荡器对温度元素引起的频偏进行补偿;孙江涛[7]等使用Kalman滤波算法分别对温度和老化两种因素的影响进行预测。本文同时考虑温度和老化两种因素,利用BP神经网络和RBF神经网络预测频偏。最后,使用合适的评价指标比较两种神经网络的预测结果,选出预测精度更高与预测效果更好的方法。
1 守时基本概述
1.1 守时基本原理
守时是指将本地频标保持在校准时间的过程。一个时间尺度的准确度总是相对于某个标准尺度而言的,守时过程中一般将GPS信号作为标准尺度,使本地频标与GPS信号的精度和准确度保持在同一水平。守时基本原理如图1所示。守时即频率漂移补偿,补偿的一般思路是利用晶振不断跟踪GPS信号,得到相对于GPS信号的频率漂移量,研究频率漂移同时间推移或同温度的变化关系,通过这种变化关系预测晶振的频率漂移量,然后将预测的频率漂移量转换成补偿电压,通过调节电压控制晶振的输出频率,使晶振的输出频率在GPS信号丢失的短时间内保持相对较高的频率准确度,从而实现守时[8-9]。
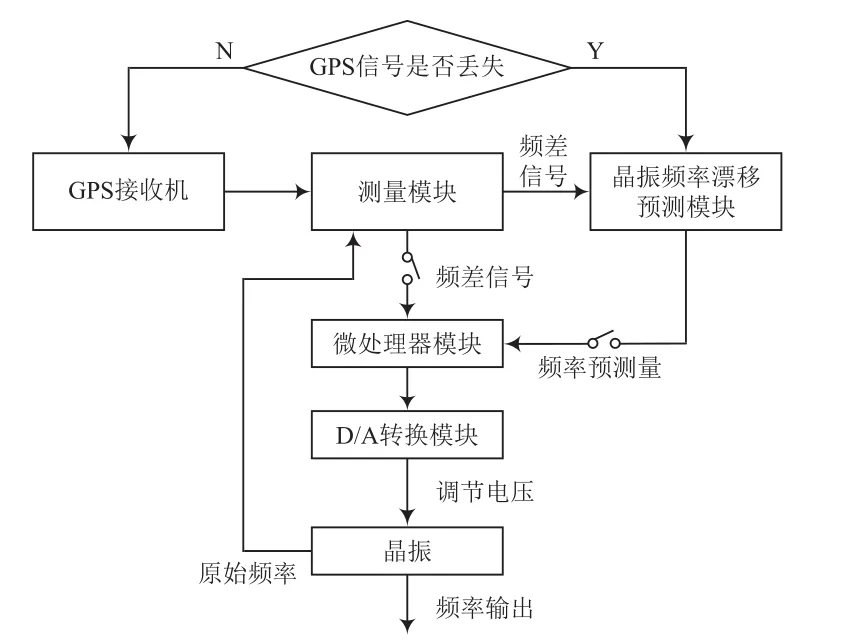
图1 守时基本原理
1.2 守时的主要影响因素
守时电路的设计、晶振本身影响因素的作用以及守时算法的编写都是影响时钟输出高精度频率的原因,而晶振本身影响因素的作用是最主要的[10]。晶振的影响因素有很多,温度和老化是影响晶振精度和准确度的主要原因。其中老化是指晶振频率随工作时间发生缓慢变化的物理现象。有研究表明,在晶振的诸多影响因素中,温度对其频率稳定性的影响是最大的[11]。
1.3 高精度守时算法概述
由于温度、老化等原因,晶振频率发生漂移。频率漂移的补偿关键在于利用历史频偏数据合理建模预测下一阶段的频偏。通常利用经验模型估计晶振的老化漂移,利用最小二乘法拟合模型预测温度漂移,但预测精度较低。且晶振实际工作过程中两种因素对频偏的影响难以被准确分开。因此可利用神经网络建立一种隐式模型,利用神经网络非线性拟合程度好、自适应性强、可用数据训练的特性拟合晶振因温度和时间引起的频率漂移,大幅提高晶振频率预测的精度。适用于非线性预测的人工神经网络主要有BP神经网络和RBF神经网络等,本文将采用这两种神经网络分别对相同的历史数据训练模型,预测失去GPS信号后的晶振输出频率。
2 BP神经网络和RBF神经网络的模型与建立
2.1 BP神经网络模型
BP神经网络的结构由输入层、隐含层和输出层组成。每一层都由一定数量的神经元构成,典型的BP神经网络结构模型如图2所示。BP神经网络在学习时,输入样本从输入层传入,经隐含层处理后传向输出层,实际输出会与期望样本进行比对,如果比对结果误差过大,则转入误差的反向传播过程,对各层神经元的连接权值和阈值进行适当修改,使误差沿梯度方向下降,反复学习训练直至均方误差满足要求。
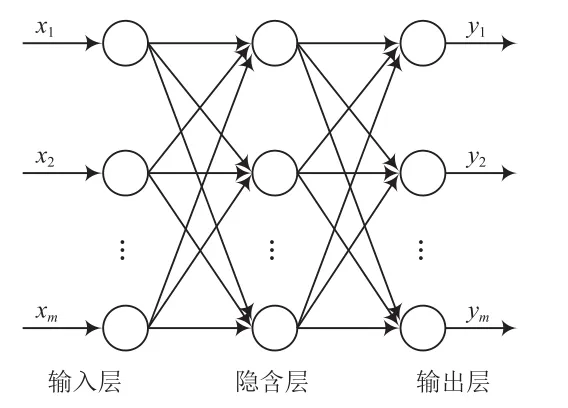
图2 BP神经网络结构
2.2 RBF神经网络模型
RBF神经网络与BP神经网络均由输入层、隐含层和输出层构成,均可拟合连续的非线性函数。不同的隐含层函数是两者的主要区别,BP神经网络隐含层的传递函数大多为非线性变换函数—Sigmoid函数,RBF神经网络的隐含层函数是径向基函数[12]。典型的RBF神经网络结构模型如图3所示,径向基函数径向对称,常用的是高斯核函数:

图3 RBF神经网络结构
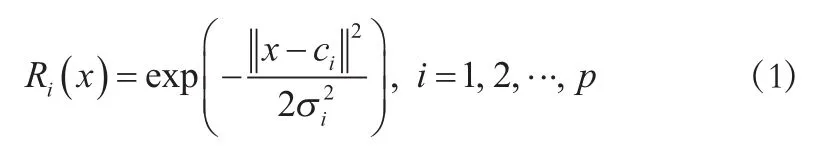
式中:x为高斯核函数的输入样本;ci为核函数的中心;σi为方差,控制函数的径向作用范围;p为感知单元的个数。RBF网络的输入层实现从x→Ri(x)的非线性映射,输出层实现从Ri(x)→yR的线性映射,即:
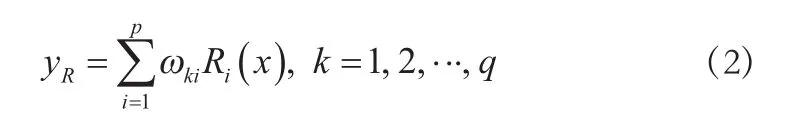
式中:q为RBF神经网络输出层神经元的个数;ωki为第i个隐含层神经元与第k个输出层神经元之间的连接权值。
2.3 数据来源
研究采用的数据集为模拟某地室外环境下晶振频率随温度和时间变化过程的数据。考虑到温度在短时间范围内变化较小且老化是个长期的过程,需要在较长一段时间的实验过程中得到实验值,所以在晶振持续工作的过程中,每隔15 min测量1次,连续测量2个月,得到数据集。其中,温度单位为℃,时间单位为h,频偏单位为Hz。部分频偏测量值见表1所列。

表1 部分频偏测量值
将数据集划分成训练集和测试集,取部分数据作为训练集数据,将训练集后一天的数据作为测试集。
2.4 RBF神经网络的构建
要实现RBF神经网络的构建,首先对数据集进行分析,步骤如下。
(1)确定输入层节点。影响晶振频率变化的因素较多,其中温度和老化是主要因素,选取温度和时间参数作为神经网络的输入层节点。
(2)确定输出层节点。频偏是指实时频率与基准频率的差值,选取频偏作为输出层节点。
(3)确定隐含层节点。隐含层节点数按照经验公式和实际试验结合的方式取值。
(4)归一化处理。考虑到温度及时间的取值范围和量纲存在较大差异,无法直接用于网络训练,所以事先进行归一化处理,把数据转化为[-1,1]之间的数值。同时为了与原输出频差作对比,预测值需反归一化处理后输出。归一化处理使得神经网络在训练过程中收敛速度更快、泛化能力更好,转化函数形式为:

式中:y为标准化之后的数据;ymax为1,ymin为-1;xmax为数据中最大的数;xmin为数据中最小的数。
(5)网络模型的训练。使用MATLAB中的神经网络训练函数(newrb函数)进行训练。输入层节点数为2,输出层节点数为1,隐含层节点数等采用newrb函数设置。分别选取前20、30、40天的数据进行训练,发现前20、30天的训练效果较差,存在欠拟合现象,所以将前40天的数据作为训练样本,以第41天的数据作为测试样本。
2.5 BP神经网络的构建
对BP神经网络进行构建时输入层节点数、输出层节点数与RBF神经网络相同。BP神经网络的隐含层传递函数选用tansig函数,输出层传递函数选用purelin函数。训练算法选用Levenberg-Marquardt算法,进行与RBF神经网络同样的归一化处理和网络模型训练。BP神经网络模型算法流程如图4所示。

图4 BP神经网络算法流程
3 神经网络预测结果与分析
使用神经网络模型算法对频偏进行预测,得到预测结果。利用预测值与实测值的最大误差、均方误差MSE和训练次数作为评估指标对预测结果进行评估。评估指标的值越小,说明预测值越接近于实测值。MSE的表达式如下:

式中:Predi为第i个预测值;Obsi为第i个实测值;n为测试集数据的数量。
3.1 RBF神经网络的预测
使用前40天的数据对模型进行训练,训练完成后,用第41天的96个数据对RBF神经网络进行测试,测试结果如图5所示。图5中Error表示预测值与实测值之差,可以看出,最大误差为0.05,均方误差为8.957 12×10-13,说明RBF神经网络的预测精度较高。

图5 RBF实测值与预测值的误差杆状图
3.2 BP神经网络的预测
使用前40天的数据对模型进行训练,训练完成后,使用第41天的96个数据对BP神经网络进行测试,测试结果如图6所示。图6中最大误差不超过0.15,均方误差为2.444 4×10-10。通过表2的评价指标对比可知,BP和RBF神经网络模型的预测值和实际输出值接近。RBF神经网络相比BP神经网络的预测精度更高,且训练时间和收敛速度更好。
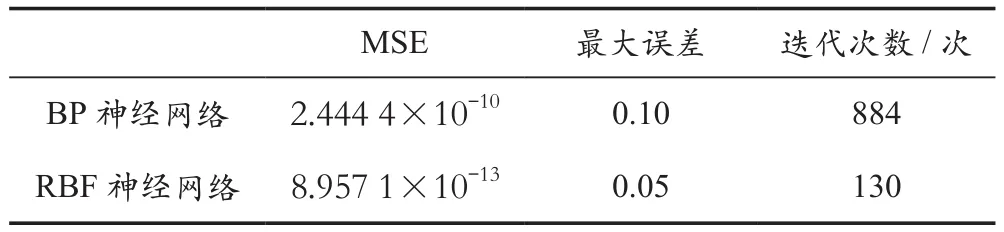
表2 2种神经网络的预测结果
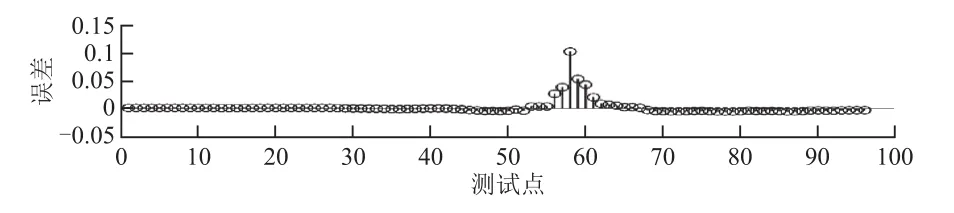
图6 BP实测值与预测值的误差杆状图
4 结 语
本研究使用神经网络预测频偏的方法使得预测值与实际值更加接近,减小了曲线拟合不精确引起的误差,提高了频偏预测精度。
神经网络训练结束后,发现2种神经网络关于温度的权值均大于关于时间的权值,这也从数据角度说明温度对晶振频率稳定性的影响是最大的。
RBF神经网络模型和BP神经网络模型经过对比后发现:RBF神经网络的预测精度较高,且训练速度更快,所以对于晶振频偏的预测而言,RBF神经网络更优,可以更好地为物联网服务。
