湖北烟草商业企业物流分类对标管理研究

余俊旸　张芬　潘回归　郭清海

摘 要：针对湖北烟草商业企业在物流对标管理中因地域差异导致的评价不公平问题，本文根据国家烟草专卖局物流对标管理分类要素体系，分别利用K均值聚类、凝聚聚类以及Birch聚类方法对湖北省17个市州进行了聚类分析。通过比较轮廓系数得分将17个市州分为四类，且三种聚类方法所得结果一致。在此基础上，进一步对湖北省17个市级烟草公司进行对标分析，验证了本文分类结果的合理性。本文为湖北省烟草商业物流分类对标管理工作提供了有意义的借鉴。

关键词：烟草物流;分类对标管理;K均值聚类;凝聚聚类;Birch聚类

中图分类号：F23 文献标识码：Adoi：10.19311/j.cnki.1672-3198.2021.14.053

0 引言

对标管理作为重要的科学管理方法在众多领域得到了广泛的应用。自2009年开始，烟草行业全面开展对标工作。在此期间，行业物流在对标管理方面也进行了许多积极探索，有力推动了行业物流管理水平的提升。然而，随着行业高质量发展要求的提出，原有物流对标体系已不能完全适应新的管理模式和运行机制的需要。存在的主要问题：一是对标管理体系不完善，二是对标指标体系不健全。其中，对标管理体系的问题主要集中在标杆的选择上。通常情况下，标杆是行业内绩效最优的某个企业。烟草行业物流对标管理，选择的标杆就是在某一指标上绩效表现最优的企业，其他企业从经营管理、产品质量、成本控制等各方面找出与标杆企业的差距并向其学习，进而弥补自身短板以提升核心竞争力。然而，只依据绩效排名确定标杆的方式，往往不具备可比性和适用性。比如省会城市，由于其先天的地理环境、人口规模、经济发展等优势，以及自身的企业规模、人力资源、技术条件等差异，其各项指标都会明显优于省内其他地市。如果统一都以省会城市为标杆的话，对一些地市特别是经济欠发达地市就很不公平，对标管理也难以起到作用。基于此原因，2019年底，国家烟草行业专卖局印发了《烟草商业企业物流分层分类对标管理规范（试行）》，对省级商业企业和重点城市商业企业试行分层分类对标管理，打响了行业层分类对標的“发令枪”。同时，鼓励各省级商业企业以《规范》为依据，构建适宜于本地的分类模型来开展地市级商业企业物流类对标管理。

分类对标首先需要解决分类问题。对目标企业进行分类的方法有很多，其中通过专家打分以及计算指标权重并加权排序等方法难免会受到一些主观影响，相对来说，利用聚类方法进行分类更加客观，因此聚类分析方法也得到了越来越广泛的应用。高珊选取降水量等指标来表现黄淮海地区的干旱程度，并利用K均值聚类法对其进行分区;肖自乾根据在线教学时学生的表现，通过K均值聚类将他们分为不同的群体，进而方便因材施教;笪可宁通过凝聚聚类法将全国35个大中城市划分为3类，再建立面板数据回归模型对影响商品住宅价格的因素进行分析;施立珊利用凝聚聚类方法对教师的教学质量进行分析;宋志飞同时采用K均值聚类、凝聚聚类、DBSCAN聚类三种方法对海南农垦耕地类型进行分析，然后通过各自的特征频数统计表来从中选中相对更优的聚类方法。王梦瑶将K均值聚类和Birch聚类结合起来对用户评论数据进行聚类。

在前人的研究基础之上，本文对湖北省17个市州的烟草物流数据进行实证研究，选取了K均值聚类、凝聚聚类、Birch聚类这三种聚类方法来分别构建分类模型，然后通过轮廓系数来比较评价聚类效果并确定最优聚类个数，最后对湖北省17个市级烟草公司进行对标分析。

1 聚类模型与评估指标

1.1 K均值聚类（K-means）

K均值聚类属于原型聚类，是应用最广泛的一种聚类方法。它首先需要自行设定聚类个数K，再从样本中随机选取K个点作为初始聚类中心，然后计算其他点与这K个中心点的距离，将每个点分配给距离最近的聚类中心，全部分好后就形成了K个簇;之后计算各个簇中的样本均值，将其作为新的聚类中心，再重复迭代计算，直到目标函数最小化，通常是使样本和所属的聚类中心之间的距离总和达到最小。

1.2 凝聚聚类（Agglomerative Clustering）

凝聚聚类属于层次聚类的一种，同样需要先指定聚类个数K，再将每个样本点都作为聚类中心，然后再将距离最近的两个类进行合并，不断重复这个过程，直到只剩下K个类。根据使用的距离计算公式不同，还可以再细分成不同的凝聚聚类算法。

1.3 Birch聚类

Birch算法的全称是利用层次方法的平衡迭代规约和聚类（Balanced Iterative Reducing and Clustering Using Hierarchies）。该算法利用可用资源生成最好的聚类结果，采用多阶段聚类技术，把待分类的数据插入一棵树中，并且原始的数据都在叶子节点上。要注意的是，Birch算法对每一个数据点的聚类决策都基于当前处理过的数据点，而不是基于全局的数据点，具体算法原理可参考文献。

1.4 轮廓系数

轮廓系数是评估聚类效果的常用指标，适用于原始数据实际类别未知的情况。假设使用某种聚类方法将样本分为了K类，然后计算每个样本的轮廓系数，用a（i）代表第i个样本与其所属类中其他样本的平均距离，用b（i）代表第i个样本与距离最近的一个类中样本的平均距离，则第i个样本的轮廓系数计算公式为：

S（i）=b（i）-a（i）max（a（i），b（i））/*MERGEFORMAT（1）

在求得了所有样本的轮廓系数后，将它们取平均就得到了最终总的轮廓系数，其取值范围为[-1，1]，越靠近1则说明聚类效果越好，反之越靠近-1则效果越差。

2 物流分类指标评价体系

为了保证所建分类模型的客观性和可比性，排除受主观因素影响较大的指标，并从客观因素中筛选出对企业物流管理影响较大的指标，并将之分为外部要素和内部要素。其中，外部要素是基本不受企业控制而只与所处地域相关的因素，包括区域经济水平、城乡结构、自然环境;内部要素则是影响物流需求与配送的主要因素，包括卷烟配送规模和卷烟零售客户。本文最终采用10项指标来构建烟草商业企业物流分类指标评价体系，具体见表1。

3 湖北省烟草商业企业物流分类及实证

综合各市州统计年鉴数据、企业内部数据和官方网站数据，本文根据2020年湖北省烟草系统17家市洲商业公司的各指标数据，分别采用K均值聚类、凝聚聚类、Birch聚类三种模型对湖北省17个市州进行聚类，并利用平均轮廓系数得分来分别评估每个模型的最优分类数。

首先对数据进行预处理，利用Python软件从Sklearn库中调用MinMaxScaler（）函数，将各维度的数据标准化到0到1之间，以消除指标间单位和尺度差异的影响。

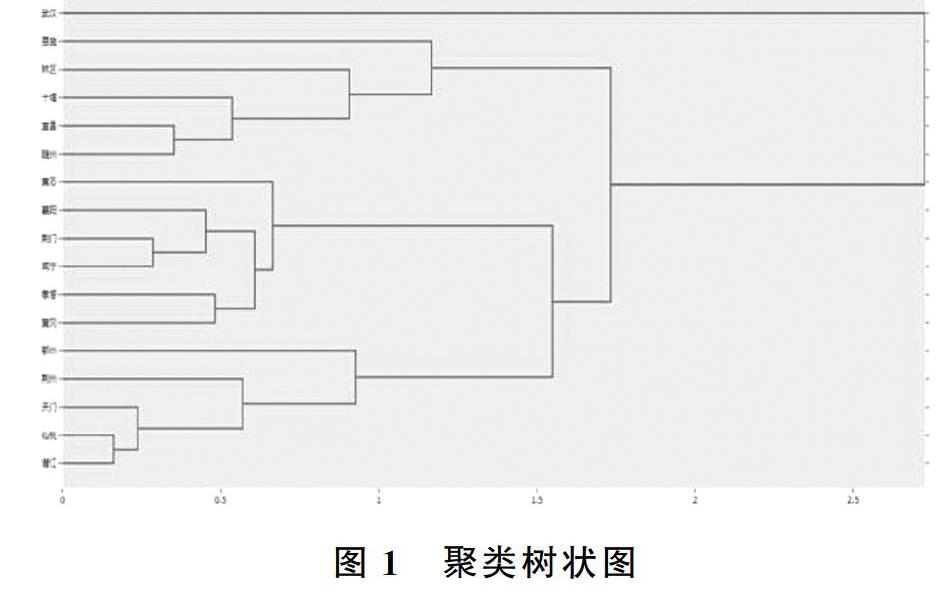
在标准化数据的基础上，先利用分层聚类方法得到聚类树状图（图1）作为分类结果的初步参考。从图1中可以看到，大体上可以把湖北省17个市州分为四类。

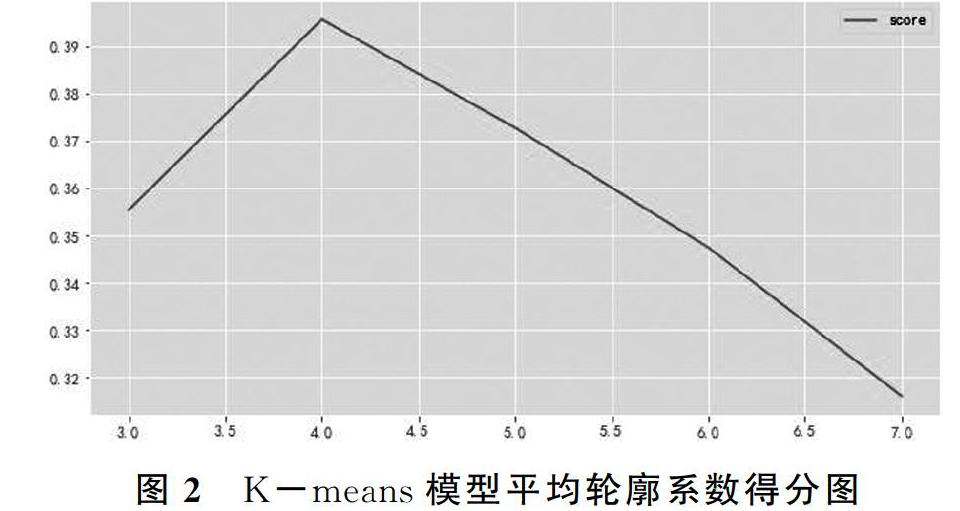
为了进一步验证分成四类的合理性，分别利用K-means模型、凝聚模型、Birch模型，选取聚类类数n从3到7，计算每种模型的轮廓系数，结果如图2-图4所示。

由图2-图4可以看出，无论是哪种模型都是当n=4时轮廓系数最大，即三种模型的最优分类方式都是将17个市州分成四类，且最终分类结果相同：武汉为一类，黄石、襄阳、荆门、孝感、黄冈、咸宁为一类，十堰、宜昌、神农架林区、恩施、随州为一类，鄂州、荆州、仙桃、潜江、天门为一类。

基于以上分类结果，对每一类计算该类10项指标的平均值，再对每项指标进行标准化，得到最终的标准分如表2所示。

由表2可见，第一类武汉，除了地形地貌指标外，在卷烟配送规模、卷烟零售客户、区域经济水平、区域城乡结构等方面的各项指标的标准分均在1.60到1.72之间，而其它三类相应的标准分均为负值，由此可看出武汉与其他三类的差距很大，因此被单独分为一类。

第二类包括黄石、襄阳、荆门、孝感、咸宁、黄冈。该类的配送总量指标的标准分远远低于武汉，但明显高于第三类和第四类。另外，该类的丘陵指标的标准分为1.70，为四类中的最高，而其它三类的标准分均为负值。

第三类包括十堰、宜昌、林区、恩施、随州。该类有一个明显特征是地形地貌中山地和高山地指标的标准分最高，分别为1.63和1.73。因此，在物流考核时要着重注意这种多山地的特殊情况。受这种情况影响，这一类的单元配送量、道路客户密度、区域客户密度、经济密度和常住人口城镇化率指标的标准分均为四类中的最低。

第四类包括鄂州、荆州、仙桃、潜江、天门。该类的配送总量指标标准分是最低的;但平均平原地形占比是最高的，其标准分达到1.08;其余指标相对来说都处于居中水平。

4 分类对标应用

以2020年1月至9月湖北省17个市级烟草公司的单箱物流成本（元/箱）、人均配送效率（箱/人）、单车日均送货数量（条）指标为例，将聚类结果应用于对标分析。

4.1 单箱物流成本分类对标

图6所示，从分类情况看，武汉市作为省会城市和区域物流中心，其物流设备设施智能化程度是其他市州无法比拟的。武汉市公司宜以自身为标杆，进行纵向对比。武汉市公司单箱物流成本为144.44元/箱，同比下降24.92%，降幅明显。第二类标杆值为148.61元/箱（咸宁），同比降幅最大-27.30%（咸宁）;第三类标杆值为123.43元/箱（林区），同比降幅最大-24.87%（恩施）;第四类标杆值为153.85元/箱（荆州），同比降幅最大-10.69%（荆州）。综合分析，除武汉外，第三类单箱物流成本平均值最低（151.19元/箱），第二类同比降幅最大（-5.82%）。第二类6个地市公司单箱物流成本平均值高于第三类和第四类，原因在于其配送总量明显高于其他两类。类中襄阳单箱物流成本最高，咸宁单箱物流成本最低，与分类指标中两地的地势地貌相关。

4.2 人均配送效率分类对标

图7所示，武汉市公司人均配送效率遥遥领先于其他公司，为1474.59箱/人，同比增长21%，增幅明显。第二类标杆值为1136.51箱/人（黄石），同比增幅最大5.24%（黄石）;第三类标杆值为918.94箱/人（宜昌），同比增幅最大3%（随州）;第四类标杆值为1342.61箱/人（鄂州），同比增幅最大5.49%（荆州）。综合分析，除武汉外，第二类人均配送效率均值最高（933.8箱/人），第四类同比增幅最大（1.58%）。第三类人均配送效率明显低于其他类，类别之间差异明显。

4.3 单车日均送货数量分类对标

图8所示，武汉市公司单车日均送货数量为5662.09箱，同比增长40.33%。第二类标杆值为6530.08箱（黄冈），同比增幅最大66.96%（黄冈）;第三类标杆值为5271.68箱（十堰），同比增幅最大40.63%（仙桃）;第四类标杆值为5490.81箱（仙桃），同比增幅最大74.44%（仙桃）。综合分析，第四类单车日均送货量均值最高（4787.89箱），第二类同比增幅最大（27.06%）。第三类单车日均送货量明显低于其他类，类别之间差异较为明显。

5 结论

（1）本文利用K均值聚类、凝聚聚类、Birch聚类三种模型对湖北省17個地市烟草企业数据进行聚类分析比较发现，17个地市烟草企业最终分为4类最为合适，其中：武汉市公司为第一类;黄石、襄阳、荆门、孝感、咸宁、黄冈为第二类;十堰、宜昌、林区、恩施、随州为第三类;鄂州、荆州、仙桃、潜江、天门为第四类。

（2）将上述分类结果应用于湖北省烟草商业企业物流对标分析，各类别之间区别很明显，准确体现了各城市在所选指标数据上的差异性，为进一步提升湖北省烟草商业企业物流对标工作科学性、可比性和适用性提供了重要依据，有助于提高对商业企业物流整体运行情况的分析和预测质量，推动行业物流高质量发展。

参考文献

[1]黄帆.关于烟草商业物流分层分类对标管理体系的思考[N].东方烟草报，2020-01-18（003）.

[2]陈昌华，黄河，尹健康，等.烟草商业企业物流对标管理分类体系研究——以四川省为例[J].中国烟草学报，2020，26（03）：114-120.

[3]高珊，陈杰，许朗，等.黄淮海地区干旱分区研究[J].节水灌溉，2020，（10）：101-106.

[4]肖自乾，陈经优.基于数据挖掘聚类算法的网络学习平台学生成绩分析[J].电脑知识与技术，2020，16（19）：28-29.

[5]笪可宁，杨贺贞.价格聚类视角下商品住宅价格影响因素实证研究[J].沈阳建筑大学学报（社会科学版），2020，22（05）：494-499.

[6]施立珊，李就娣，莫卓达，等.聚类分析在高校教务系统中的应用研究[J].电脑知识与技术，2016，12（13）：18-20.

[7]宋志飞，彭金莲.海南农垦耕地类型的聚类分析[J].计算机应用研究，2020，37（S1）：88-91.

[8]王梦遥，王晓晔，洪睿琪，等.基于改进BIRCH聚类算法的评价对象挖掘[J].软件，2019，40（11）：9-12+61.

[9]尚家泽，安葳鹏，郭耀丹，等.基于阈值的BIRCH算法改进与分析[J].重庆邮电大学学报（自然科学版），2020，32（03）：487-494.