高阶谐波控制算法减振应用中作动器饱和问题研究

张仕明， 周 云， 胡和平

(直升机旋翼动力学重点实验室，中国直升机设计研究所，江西 景德镇 333000)

直升机前飞时桨叶在各个方位角的气流速度不同，旋翼处于不对称、非定常、周期变化的气动环境中，必然产生高阶谐波气动载荷，它是直升机振动的主要根源。在过去的三十年里，为了减小旋翼振动，涌现出了多种主动控制旋翼技术。

基于减振的旋翼主动控制起源于“高阶谐波控制”(higher harmonic control，HHC)[1]，其通过在自动倾斜器不动环上施加N/rev激励(N为旋翼桨叶片数)，使旋转桨叶获得N/rev、N±1/rev的桨距输入，进而在桨叶上引起附加的高阶气动载荷，选择适当的激励幅值和相位，就能抵消原桨叶的交变载荷，降低桨毂中心的力和力矩的N/rev谐波分量，从而从源头实现直升机减振。HHC系统受到高功耗、带宽以及每片桨叶桨距输入一致等条件的制约，其一种替代方法为“独立桨叶控制”(individual blade control，IBC)，传统的IBC[2]通过小拉杆在旋转系统下独立控制每片桨叶根部桨距输入，其克服了HHC的一些限制，允许每片桨叶控制输入不同。其原理与HHC类似。IBC的另一种实施方案为在桨叶上引入控制装置(on-blade control，OBC)。OBC相比HHC和小拉杆式IBC有很多优势，如低的多的驱动功耗，易于实现高频、宽频带驱动，特别是OBC装置的失效不会影响飞行安全。

现有的OBC技术中，主动控制后缘襟翼(actively controlled flap，ACF)最为成熟[3-4]，其通过驱动如图1所示的后缘襟翼挥舞抵消不利的桨叶高频气动载荷。不管是HHC还是IBC旋翼，其减振控制策略都源于HHC算法。HHC算法假设振动的主要谐波成分与选择的高阶谐波控制输入之间为静态线性关系，即线性时不变(linear-time-invariant，LTI)系统，则系统可以用传递函数矩阵或状态空间来描述[5]。基于LTI假设的HHC法可根据开环过程进行传递函数的估计和控制器增益的更新进行自适应控制。典型的控制律可通过无约束优化方法，如最小二乘法进行构造。

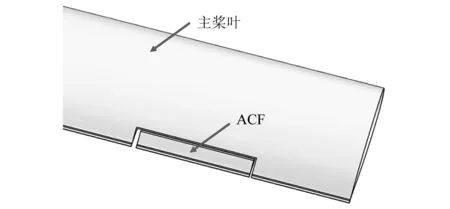
图1 ACF桨叶示意

然而ACF装置的驱动器能力有限，在试验、试飞中常常出现幅值受限的情况。饱和会在线性系统中引入了非线性，迫使控制系统在非设计模式下工作，极大的降低了控制性能。此时通常对信号在时域进行截断或缩放来消除饱和，其中截断法为：对信号超过饱和限制的部分直接削去，缩放法为:均匀的按比例缩小襟翼偏转信号，使得最大值小于限制值。然而这些方法将导致控制器性能严重降低。Cribbs等[6]提出了一种迭代增加或减小目标函数中控制信号相关权重矩阵的方式来解决作动器饱和问题，即自动权重法(AW)。尽管AW法性能优异，然而自动权重法需要对优化的控制权重上限进行先验猜测，需要多次迭代才能收敛。且对多小翼情形，如后缘襟翼+格尼襟翼(gurney flaps)，当多个小翼的控制权重相同时，控制输入将仅对其中1个小翼最优。当多个小翼的控制权重不同时，计算量将显著增加，以致AW法不再适用[7]。AW法的缺点可通过约束优化方法解决，Roget等[8]提出了采用序列二次规划(SQP)求解HHC中的最优控制输入信号，其将作动器饱和约束等效转化成以小翼控制谐波信号正弦、余弦幅值为变量的非线性不等式约束，结合HHC算法中的二次目标函数，形成了一个非线性规划(NP)问题，再通过SQP法对该问题求解。仿真表明该方法得到的减振性能优异。Friedmann等[9]研究表明SQP方法在双小翼构型中优异性更加显著，计算效率相比AW法显著提高，然而SQP[10]求解计算复杂，其迭代收敛时长可达秒级。Morales等[11-13]提出了基于线性约束的二次规划(QP)法求解带约束的HHC问题，其将非线性约束近似转化成线性约束条件，如盒型约束、1-范数约束、∞-范数约束，相比SQP法计算效率显著提高，其中1-范数约束性能最优，已在多自动倾斜器主动控制旋翼试验中应用[14]。但其优化结果仍存在保守，给定任意控制频率的最大幅值，该方法将引起0%到约30%的控制幅值损失。

本文提出了一种最优解落在限制值上的迭代-QP方法(Iter-QP)，其通过对控制信号中各阶谐波的复数坐标系进行变换，扩大上一步中1-范数约束QP法(1N-QP)最优解附近的可行域，使得迭代收敛的最优解的幅值和等于限制值。相比1N-QP法适用性和控制性能显著提升，且单步计算效率几乎无减小。该方法不受控制信号谐波数量和控制面数量的影响，收敛解在频域非线性约束条件下无保守。能够满足主动控制旋翼控制系统的工程运用。

1 HHC算法

HHC法属于频域方法，常用于扰动(振动或噪声)频率成分已知的情形。其基于线性模型假设，即直升机稳态前飞时控制输入u和输出y之间为线性关系。在HHC算法中，测量的振动和控制输入的更新为间断的，时间为tk=kτ，τ表示控制对象的输出重新达到稳态的更新周期，在实际操作时，常常选为旋翼周期的整数倍。无控时振动d随直升机飞行状态变化而变化，则旋翼系统模型可表示为：

yk=Tuk+d

(1)

式中，当控制输入为零(uk=0)，yk=d。在初始状态，即k=0时，式(1)表示为

y0=Tu0+d

(2)

公式(1)、(2)相减，消去扰动d，得到

yk=y0+T(uk-u0)

(3)

式(3)也被Johnson[5]称作直升机响应的全局模型。传递矩阵T可通过离线或在线识别得到。

基于最小化振动水平和控制信号能量的二次目标函数Jk为

(4)

式(4)中Q、R为对角权重矩阵，常设为单位阵，对目标函数求偏导，令

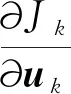
(5)

得到优化控制律uk,opt如下

uk,opt=-(TTQT+R)-1(TTQ)(y0-Tu0)

(6)

式(6)为HHC控制律的一个经典表达形式，然而其是在无约束优化条件下得到的，常常超出驱动器的能力限制。采用缩放、截断可导致控制性能变差，自动权重需要对权重矩阵上限进行先验猜测、SQP法计算复杂。为了更好的解决驱动器饱和问题，Morales等[11]引入二次规划算法，其具有结构简单、便于求解等特点。将式(1)代入(4)，得到关于优化变量uk的二次目标函数：

(7)

2 作动器约束

控制信号约束在时域的表达形式为：

(8)

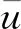
(9)

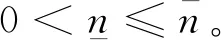
(10)

该时域约束可用傅里叶系数在频域等价表示为[16]：

(11)

图2 控制输入域示意

2.1 1-范数近似

二次规划要求约束函数都是线性的，显然约束式为非线性，因此须将其转化成线性不等式。定义控制输入向量u为：

(12)

一种便于求解的约束转化方式为1-范数：

(13)

当m=1时，其表示的几何区域如图 2中S1所示。显然，1-范数近似约束的不等式数量不随u的维数2m变化而变化，始终只有1个不等式，因此随维数2m越大，QP求解的速度优势越明显。但其优化结果仍存在保守，给定任意控制频率的最大幅值，存在：

(14)

因此，1-范数近似约束最优解可能存在0%到约30%的控制幅值损失。

2.2 u幅值和usum的线性化

为了解决这个问题，本文提出了一种最优解落在限制值上的迭代-QP方法。

令uopt与Ox轴的夹角为α，很容易构建旋转矩阵P，使得向量uopt落在坐标轴Ox′上：

u=Pu′

(15)

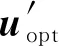
(PTTTQd)Tu′k

(16)

相应的1-范数约束为

(17)

对坐标系Ox′下的QP问题进行求解，如此迭代，显然，收敛得到的最优解ulim满足：

(18)

且每一个迭代步的解始终满足约束域S。

类似的，当m>1时，可根据uopt对每一阶谐波单独进行坐标系的旋转变换，令向量uopt的正弦分量为0，再构建一个可逆矩阵V，令uopt的所有余弦分量相加，得到：

(19)

显然，迭代收敛时，最优解ulim将满足：

(20)

3 仿 真

为了验证本文提出的方法，以ADASYS(adaptive dynamic system)旋翼[3]为对象开展减振控制仿真研究。ADASYS旋翼是德国宇航中心(DLR)研制的一副4片桨叶带主动控制后缘襟翼旋翼系统，其安装于BK117平台上于2005年完成了飞行演示验证。对减振控制，通过开环试验，获得了ADASYS旋翼的在Laplace域下传递函数特性。

yHub=G(s)uHHC+dHub

(21)

其中，

uHHC=[ucollulongulat]T

yHub=[FzMxMy]T

式中:Fz为4/rev桨毂升力、Mx为4/rev桨毂俯仰力矩、My为4/rev桨毂滚转力矩、ucoll为总距输入、ulong为纵向距输入、ulat为横向距输入、G为传递函数。

185.2 km/h水平前飞时，识别出的传递特性如下，下面将利用该参数对本文的抗饱和高阶谐波控制算法进行仿真。

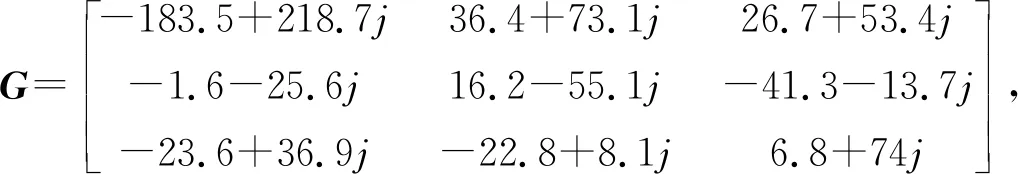
(22)

传递函数G对应的控制输入来自固定坐标系下的低阶谐波(此处为0、1/rev)，其与旋转坐标系下高阶谐波周期信号对应的关系为[15]：

式中X表示固定坐标系低阶谐波输入与旋转坐标系下高阶谐波控制输入之间的线性关系。则旋转坐标系输入对应的传递矩阵T可表示为

(24)

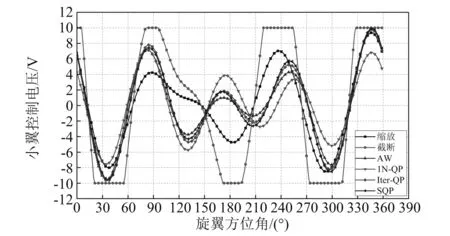
图4 小翼最优控制信号

图5 减振效果对比

表1 最优控制信号各阶谐波正弦、余弦分量

从仿真结果可看出：

(1)在所讨论的抗饱和HHC方法中，除基于非线性约束的SQP外，Iter-QP法性能最优。Iter-QP法每一个迭代步的减振效果都不低于1N-QP法，如图3所示，第7步时Iter-QP法的目标函数J收敛，J减小达到93.3%。

图3 目标函数J减小百分比随迭代步数变化

(2)Iter-QP法与SQP法的最优控制信号各阶谐波分量、各通道减振效果相近，进一步验证了Iter-QP法的思路可行性和减振能力。

(3)抗饱和优化方法AW、1N-QP、Iter-QP的减振效果明显优于传统的缩放和截断法，J减小都达到90%以上。

(4)采用Matlab工具箱在3.4 GHz Intel Xeon E3处理器上分别对Iter-QP法和SQP法进行仿真，Iter-QP法单步计算耗时约5.0 ms、SQP法耗时约28.7 ms。频域HHC法控制指令常采用旋翼旋转3圈更新1次，第1圈计算控制指令，第2圈发送新的控制信号，第3圈采集瞬态衰减后的振动信号。有时为了等待瞬态的衰减，等待时长可能达到1 s[16]。以额定转速17 Hz的4 m直径模型马赫数相似旋翼为例，其旋翼旋转1圈时长约58.8 ms，远大于5.0 ms，而全尺寸旋翼旋转周期更长，因此Iter-QP法的计算效率可以满足工程运用。

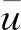
表2 不同控制输入下1N-QP与Iter-QP法对比

4 结 论

旋翼是直升机振动与噪声的主要来源，ACF旋翼可从源头进行减振、降噪，此外研究发现，其还具有性能提升、在线锥体平衡等能力，其中减振效果最为明显，受到广泛关注。本文针对减振应用，基于经典的HHC算法开展了作动器饱和约束条件下的最优控制问题研究，结论如下：

(1)本文提出的迭代-QP法可有效提升减振性能，减振能力可达到基于控制信号的各阶谐波幅值之和约束的SQP法。

(2)迭代-QP法计算效率高，单个迭代步的计算量相比1-范数-QP法几乎无增加，每一个迭代步控制输入都满足约束，且减振性能更优。

(3)相比1-范数-QP法，迭代-QP法最优控制信号幅值和保守小，减振效果更优。

(4)根据迭代-QP法利用单步最优解构建可逆矩阵进行坐标系变换，扩大最优解附近可行域的原理，其对多目标、多小翼情形同样适用。