基于概率论的爆破振动傅里叶主频预测

2021-06-30邓冰杰王林峰李林刚

振动与冲击 2021年12期

邓冰杰，王林峰，李振，李林刚，莫诎

(1. 重庆交通大学河海学院，重庆 400074； 2. 中交二航局建筑科技有限公司，武汉 430040； 3. 中交第二航务工程局有限公司，武汉 430040； 4. 重庆交通大学山区公路水运交通地质减灾重庆市高校市级重点实验室，重庆 400074；5. 重庆交通大学土木工程学院，重庆 400074)

爆破振动对建(构)筑物的影响一直都是爆破安全施工关注的问题。随着对爆破振动研究的深入，研究人员普遍意识到建(构)筑物的爆破振动破坏不仅取决于振动峰值振速，与振动频率和持续时间也密切相关[1]。目前，国内外常用的爆破安全控制判据基本都是“主振频率-峰值振动速度”判据[2]，如德国标准(DIN 4150-3)、英国标准(BS 7385-2)、法国标准(87/70558)、美国标准(USBM)、印度标准(directorate general of mines safety)、土耳其等采用的爆破振动控制标准及我国2014版的GB 6722—2014《爆破安全规程》[3]。

由于爆破振动频率离散性较大，相对于爆破振动强度预测的研究，对于爆破振动频率预测的研究相对较少[4]。就目前的研究现状来看，预测方法可以分为三类：半理论半经验公式；智能算法预测；基于振动波形预测的主振频率预测。

经验(半理论半经验)公式预测方面。早期，前苏联学者、焦永斌[5]、唐春海等[6]分别提出了含单一未知参数的爆破振动主频预测公式。张立国等[7-8]基于相似准数方程、孟海利等[9]基于地震波在黏弹性介质中的传播理论分别提出了包含两个待求参数的预测公式；陈博闻[10]基于量纲分析建立了爆破振动频率的相似准数方程，提出了考虑炮孔深度的爆破振动主频率的预测公式。

近年来，卢文波教授及其团队在主振频率预测方面做了较多的研究，卢文波等[11]基于弹性介质中球状药包激发引力波的理论解及其频谱表达式，提出了质心频率的预测公式；周俊汝等[12]指出相较于傅里叶主频，平均频率的随爆心距的衰减规律更加显著，利用反幂函数拟合频率与爆心距的变化规律，平均频率的相关系数更高；卢文波等[13]基于量纲和谐原理和球面波理论推导主频预测公式，并指出采用柱面波理论拟合的主频衰减公式拟合相关系数较基于球面波的主频衰减公式总体稍高；刘达等[14]采用量纲分析的方法，从结构动力学的角度得到的爆破振动主频衰减公式，指出在爆破振动主频的选择上，视主频相较于傅里叶主频能够更好的反映爆破振动的频率特性。叶红宇等[15]结合C40混凝土试块的爆破累积试验提出了同一介质中的傅里叶主频预测公式。周俊汝等[16]基于弹性波动理论，研究了竖向钻孔爆破激发的振动波频率衰减特征，指出主频衰减过程中易发生突变，质心频率的衰减规律相对平滑稳定。

智能算法预测方面。张艺峰等[17]提出了基于BP神经网络理论的预测方法、周玉纯等[18]提出了基于粗糙集理论的模糊神经网络(RS-FNN)预测方法。Singh等[19-21]采用神经网络算法(ANN)模型对爆破振动主振频率f进行了预测。Li等[22]提出了一种基于灰色关联分析和量纲分析相结合的主振频率预测方法。

基于振动波形预测的主振频率预测方面。Blair[23]根据爆破孔之间的间距提出了一种非线性叠加模型，实现了多孔微差爆破振动波形的预测。杨年华等[24]根据场地地震波的传播叠加原理，以实测单炮孔爆破振动波形为基础，计算获得预测点的爆破振动波形。雷振[25]对Anderson线性叠加模型进行改进，提出了一种非线性叠加模型，并建立了基于Volterra泛函级数的台阶爆破振动预测模型；杨年华[26]利用单孔振源的格林函数来叠加合成群孔爆破振动时程，实现了对爆破振动峰值速度、频率及持续时间的预测。雷振等[27]提出了一种基于三次B样条的爆破振动历程预测方法。刘小鸣等[28]在球形药包的地表振速波形函数的基础上，通过叠加法得到了单孔柱状药包的振速波形函数，并借鉴了Blair的非线性群孔叠加理论，提出了振动波形函数预测法。

表征爆破振动主频的特征频率包括视主频、傅里叶主频、拟速度反应谱主频和质心频率(加权平均频率)等，到底哪一种特征主频与结构的爆破振动破坏关系最密切，目前没有一个统一的认识。就工程实际而言，采用的较多的依旧是傅里叶主频，比较实用的预测公式主要是半理论半经验公式。考虑到傅里叶主频的接受度较高，本文研究对象为傅里叶主频。同时考虑到各种预测公式的预测结果总是与实际值存在一定的误差，但是实测值基本在预测值附近波动，因此本文在提出基本公式预测模型的基础上将概率论的思想引入到傅里叶主频的预测中。

1 傅里叶主频预测公式及参数求解

1.1 主频预测公式分析

目前的工程实际，采用的较多的是基于最大单段装药量和爆心距的半经验半理论公式，通过线性回归得到预测公式中的两个参数。经验公式如果直接进行非线性回归，无法求得解析解，只能通过迭代法求解数值解。吕涛等对比了非线性回归和线性回归的结果，指出两种回归方法得到的预测公式的标准残差平方和非常接近，采用两种方法都是可行的。考虑到线性回归方法比较容易实现，工程使用方便，因此在参数求解时将非线性问题转化为线性回归问题。

(1) 张立国公式

(1)

式(1)可转化为

(2)

等式(2)两边求对数得

ln(fR)=lnK+αln(Q1/3/R)

(3)

(2) 孟海利公式

(4)

式(4)可转化为

(5)

(3) 卢文波等提出的公式

基于球面波理论

(6)

式(6)可转化为

(7)

式(7)两边求对数得

ln(fQ1/3)=lnK+βln(Q1/3/R)

(8)

基于柱面波理论

(9)

式(9)可转化为

(10)

式(10)两边求对数得

ln(fQ1/2)=lnK+βln(Q1/2/R)

(11)

(4) 叶红宇等提出的公式

(12)

等式(12)两边去对数

lnf=lnK+αln(Q1/3/lgR)

(13)

(5) 本文提出的基本预测公式

总结现有的主振频率的预测公式，可以看出研究者普遍认为主振频率预测公式主要包含受单段最大装药量和爆心距两个参数。因此本文提出如下的主振频率预测公式

f=KQαRβ

(14)

等式(14)两边取对数得

lnf=lnK+αlnQ+βlnR

(15)

1.2 基于最小二乘法的预测模型参数求解

(1) 一元线性回归

对于张立国公式、孟海利公式、卢文波公式和叶红宇公式在参数求解时都可以转化为一元线性回归问题。目标函数为

y=ax+b

(16)

(17)

(18)

将式(17)代入式(18)整理得

(19)

求解式(19)得

(20)

(2) 二元线性回归

对于本文推荐的基本公式预测模型，可转化为二元线性回归问题。

令

Z=lnf

(21)

X=lnQ

(22)

Y=lnR

(23)

γ=lnK

(24)

式(21)～(24)代入式(15)得到目标函数

Z=αX+βY+γ

(25)

(26)

由级值定理有

(27)

式(27)可进一步转化为

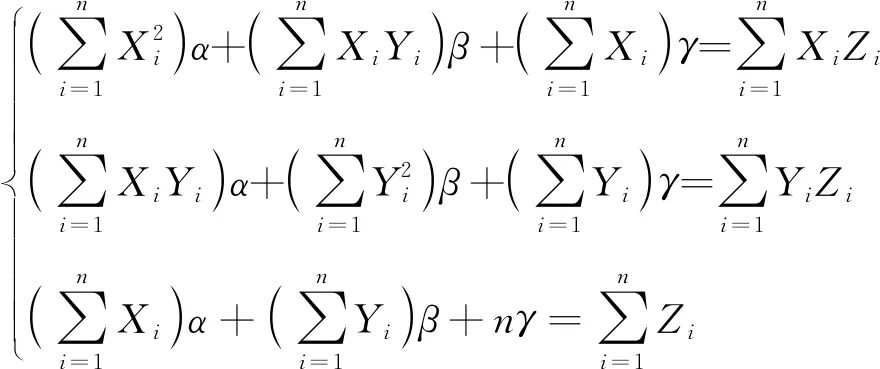
(28)

令

(29)

(30)

M=(αβγ)T

(31)

当A≠0时，线性方程组可求得M的唯一解

M=A-1B

(32)

由于各公式经过不同的变换之后转化为线性函数，X、Y、Z的表达式不一致，不同公式基于最小二乘法的求解得到的参数是使不同的目标函数实测值与目标函数预测值之间偏差平方和RSS[如式(17)和式(26)]最小，但是并不是使主振频率f残差平方和RSS[如式(33)]最小。为了区分各公式拟合结果的优劣，这里采用残差平方和RSS作为统一的优劣判别标准。

残差平方和

(33)

2 基于正态分布的主振频率预测模型

2.1 基于正态分布的主频预测模型的建立

由于爆破振动的复杂性和随机性，以及监测仪器工作的不稳定性，即使在相同爆破参数和爆心距条件下，振动主频也不是一个确定的值，实测值往往在预测值上下进行波动，因此这里考虑引进概率论的思想对主振频率预测公式进行修正。同时，考虑到现场实际振动主频越大，傅里叶主频预测速度与实际傅里叶主频的绝对误差出现较大值得可能性就越大。因此，不同爆破参数对应的主振频率的分布函数方差是不一样的，表现为主振频率越大，分布函数方差就越大。

定义主振频率相对误差(relative error of main vibration frequency，REMVF)

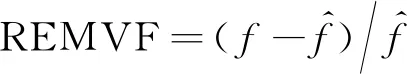
(34)

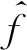
假设

REMVF～N(0,σ2)

(35)

式(35)中

(36)

(37)

由式(34)可得

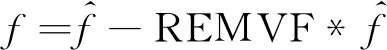
(38)

由正态分布的传递性，可得在已知某一爆破参数下(Q、R确定)，爆破振动主振频率分布函数为

(39)

振动速度的分布函数为

(40)

为了方便计算，对式(39)做一下变换，转化为标准正态分布[30]。令

(41)

根据分布函数的意义，则有

(42)

2.2 爆破参数确定下频率分布在某一区间的概率计算

由分布函数的意义可知，在爆破参数和爆心距已知的情况下，就可以算出主振频率分布在具体区间范围[f1,f2]的概率，如下式所示，基于此可以对爆破振动主振频率进行一个提前的预估。

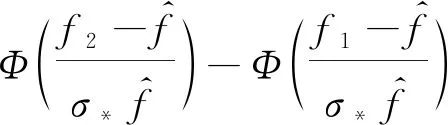
(43)

令

(44)

(45)

通过查标准正态分布表，就可以得到

P(f1≤f≤f2)=Φ(m2)-Φ(m1)

(46)

2.3 特定双侧置信度下的频率范围预测

当双侧置信度M确定时，查阅标准正态分布表可以得到m1和m2，其中m1和m2互为相反数。以本文提出的基本公式作为预测模型有

f1=(σ*m1+1)KQαRβ

(47)

f2=(σ*m2+1)KQαRβ

(48)

根据“小概率事件”的基本思想，小概率事件通常指“发生概率小于5%的事件”，该事件被认为在一次试验中发生的概率几乎为0。因此，建议取双侧置信度为95%，即：确保爆破主振频率在该频率区间的概率为95%。查阅标准正态分布表，当双侧置信度为95%时，m2=1.96，m1=-1.96。

3 工程实例验证

现场爆破数据采集依托于贵安新区核心区污水处理厂尾水排放通道工程2标段，隧道为圆拱形断面，断面面积为17.8 m2，采用全断面爆破开挖。现场监测仪器为成都交博科技M20型爆破测振仪，每次监测采用3台仪器。现场监测仪器布置如图1所示。实测数据表明：隧道沿线地表爆破振动三个方向分量中重力方向振动速度最大，典型三分量振动曲线如图2所示；隧道内侧壁爆破振动三个方向分量中水平径向(即垂直侧壁表面方向)振动速度最大，典型三分量振动曲线如图3所示。本文研究对象为峰值速度最大的方向分量对应的傅里叶主频,隧道沿线地表为重力方向振动傅里叶主频；隧道内侧壁为水平径向振动傅里叶主频。在隧道内侧壁采集了48组数据，统计如表1所示；在隧道沿线地表采集18组数据(其中1组数据无效，有效数据17组)，统计如表2所示。共计65组有效数据。

图1 现场振动监测仪器布置

图2 隧道沿线地表典型振动曲线

图3 隧道内侧壁典型振动曲线

图4 隧道内侧壁部分振动信号的FFT频谱

表1 隧道内侧壁实测振动数据统计

表2 隧道沿线地表实测振动数据统计

根据现场实测数据，分别采用张立国公式、孟海利公式、卢文波等基于球面波理论和柱面波理论分别提出的两个预测公式、叶红宇等提出的公式和本文提出的基本公式，采用非线性问题线性化的思路，基于最小二乘法原理得到的回归结果，如图5～图10所示。

图5 张立国公式预测结果

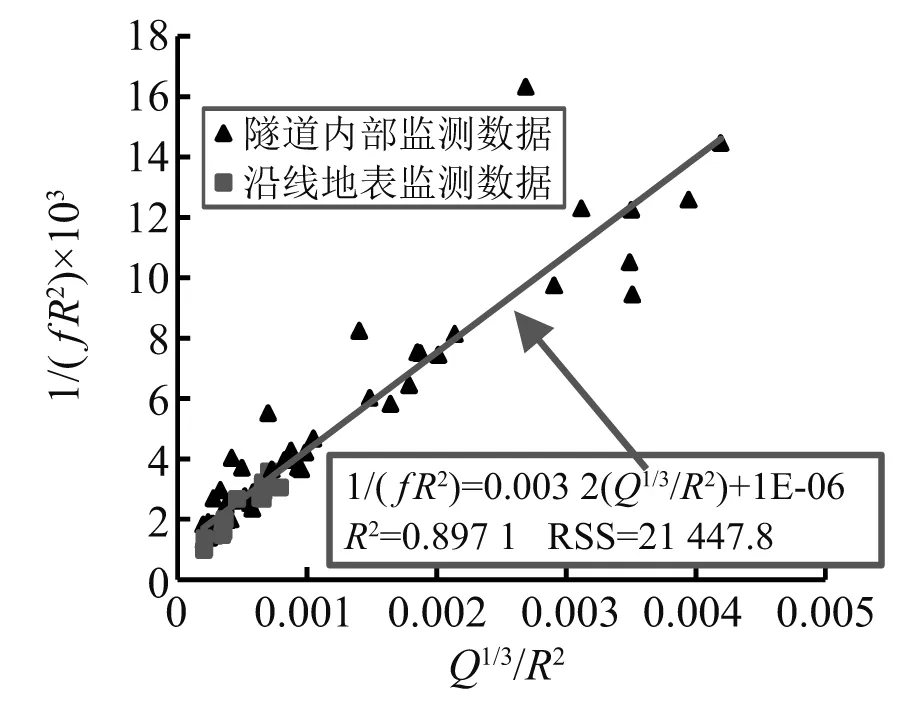
图6 孟海利公式预测结果

图7 基于球面波理论的预测结果

图8 基于柱面波理论的预测结果

图9 叶红宇公式预测结果

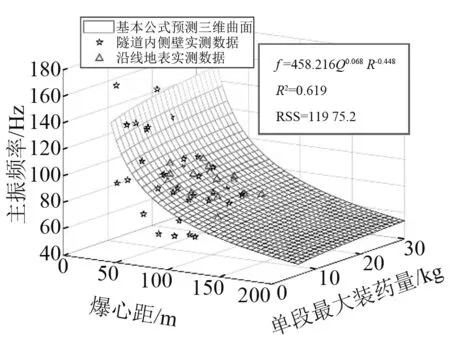
图10 本文提出公式的预测结果

各预测模型的回归系数和残差平方和统计，如表3所示。比较6种预测模型的回归系数R2和残差平方和RSS，可以得出结论：采用不同的回归模型，并通过变形将非线性问题转化为线性回归问题，基于最小二乘法原理进行回归拟合得到的回归系数R2越高，式(33)计算得到的傅里叶主频预测残差平方和RSS并不一定越小，因此并不代表预测效果越好。因此，对比分析中应采用式(33)所示的残差平方和RSS这一参数来反映拟合结果的优劣。6种预测模型中，本文提出的基本公式预测模型的拟合结果的RSS最小，拟合效果是6种预测模型中最优的。

表3 六种预测模型的回归系数和残差平方和统计表

因此本工程推荐的傅里叶主频预测模型为

f=458.216Q0.068R-0.448

(49)

通过对广义REMVF的统计分析得到，广义REMVF的平均值为0.012 18(非常接近0)，标准差为σ*=0.149 5。故傅里叶主频的分布函数为

(50)

式(50)中

(51)

为了验证式(51)的正确性，引入正态分布理论中的“3σ准则”。μ为平均数，σ标准差，“3σ准则”具体表述为：

假设：x～N(μ,σ2)。则：x的值分布在(μ-σ,μ+σ)区间的概率为0.652 6；x的值分布在(μ-2σ,μ+2σ)区间的概率为0.954 4；x的值分布在(μ-3σ,μ+3σ)区间的概率为0.997 4。

如图11所示，实测数据全部分布在预测值3σ上限和3σ下限之间，这说明实测数据基本符合“3σ准则”，这说明式(35)的假设是合理的。因此，修正的主振频率预测模型可以有效的预测傅里叶主频可能出现的区间范围。图12为双侧置信度取95%时依托工程傅里叶主频关于最大单段装药量Q和爆心距R的分布区间的三维网格图。

图11 主振频率实测值与预测值之间的关系

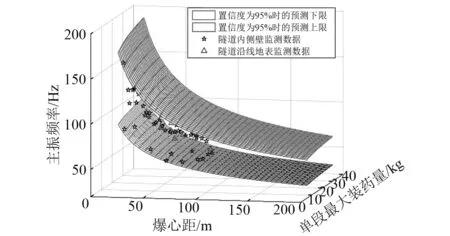
图12 傅里叶主频随爆破参数的分布区间图

取双侧置信度为95%时，最大单段装药量为Q、爆心距为R时傅里叶主频取值上限和取值下限计算如下

f1=(σ*m1+1)KQαRβ=(0.149 5×(-1.96)+1)×458.216Q0.068R-0.448=323.95Q0.068R-0.448

(52)

f2=(σ*m2+1)KQαRβ=(0.149 5×1.96+1)×458.216Q0.068R-0.448=592.482Q0.068R-0.448

(53)

傅里叶主频取值区间为：[323.95Q0.068R-0.448,592.482Q0.068R-0.448]。

4 结论

(1) 爆破振动主频包括：视主频、傅里叶主频、拟速度反应谱主频和质心频率，其中傅里叶主频最为经典，采用也是最多的，因此本文以傅里叶主频为研究对象。在总结现有特征主频预测模型的基础上提出了基本公式预测模型f=KQαRβ，并基于非线性问题线性化的思想给出了基本公式预测模型参数求解过程。

(2) 基于现场实测数据，以傅里叶主频为研究对象，比较了张立国公式、孟海利公式、卢文波等分别基于球面波理论和柱面波理论提出的两种公式、叶红宇等提出的公式和本文提出的基本公式这6种预测模型的预测结果。指出了以回归系数R2作为标准来判别预测优劣的不足之处，提出应以残差平方和RSS作为预测相对优劣的判别标准。实测数据表明：采用本文提出的基本公式预测得到的残差平方和最小，预测效果是六种预测公式中最优的。