基于谱线特征的OFDM 与FBMC 多载波波形识别

邵 凯 ，李 慧 ，周娟红

（1.重庆邮电大学 通信与信息工程学院，重庆 400065；2.重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065）

0 引言

在移动通信系统的不断演进过程中，针对第六代移动通信系统（The 6th Generation Mobile Communication System，6G）的探索已逐步进行[1]，且6G 对多种多样的应用及各种服务提出了更高的需求[2]。因此其物理层调制波形需要满足各种各样的情况[3]。文献[4]和文献[5]中提出不同的场景需要灵活适配不同参数波形来传输。

5G 及未来的通信也不断针对新波形进行相应的探索[6]。正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）使用正交振幅调制（Quadrature Amplitude Modulation，QAM）信号，是5G 的波形之一[7]。为了满足对异步传输的需求，需要考虑OFDM 中所存在的同步和正交[8]问题。Gabor 理论中具有很多限制条件，但都由于OFDM 的正交性而不能摆脱这些限制，而非正交无线通信技术却能够很好地解决所出现的这些问题[9]。随后基于滤波器组的多载波（Filter Bank-based Multicarrier，FBMC）被提出，其所用的偏移正交调幅技术（Offset Quadrature Amplitude Modulation，OQAM）有效解决了现有正交技术中所存在的问题[10-11]。FBMC 由于其存在不易实现及不易结合现有技术等缺点，没有被过多地考虑[12-13]。

目前，在信号调制识别领域已经做了大量的研究[14-17]，且在多种方面取得了较好的识别效果。文献[18]中的特征参数考虑使用高次方傅里叶谱；文献[19]提出基于谱线特征的卫星通信调制识别技术；文献[20]根据信号功率谱旁瓣衰减所呈现的特点进行识别，但其在低SNR下的效果不好。

本文首先简要介绍了OFDM、FBMC 信号的信号模型，并推导了OFDM、FBMC 信号的二次方谱线；然后在高斯噪声下进行了OFDM 及FBMC 信号的调制识别分析；最后对OFDM 与FBMC 信号的谱线出现的位置与强度及调制识别进行了仿真分析。

1 OFDM/FBMC 信号模型

理想的连续时间OFDM 基带信号为：

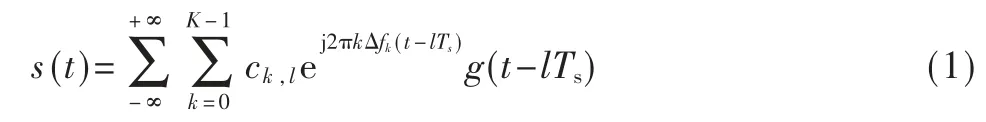
式中，K 表示子载波的个数，Δfk表示频率间隔，Ts表示符号的周期，g（t）常使用矩形脉冲成型的函数。

理想连续时间的FBMC 基带信号表示为：

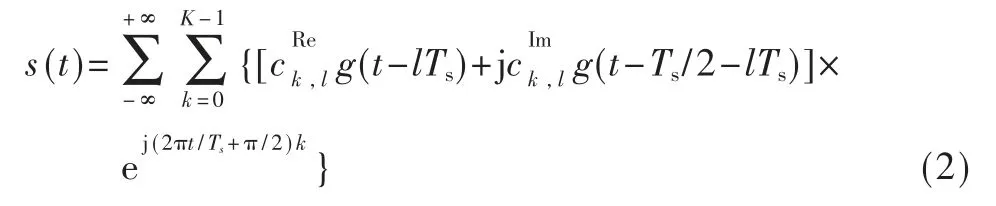
假设每个子信道相互独立，数据符号满足均值为0 且独立同分布，即E表示方差。

s（t）表示OQAM 中K 个统计独立子信道之和[21]，表示为：

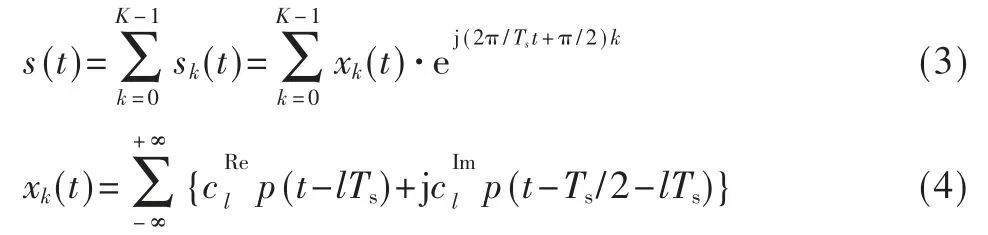
其中，k=0，1，…，K-1；xk（t）表示子载波上调制信号OQAM。

2 谱线特征分析

2.1 子载波星座调制信号的二次方谱分析

本文中的OFDM 系统以QAM 信号调制为例。QAM信号的基带信号可以表示为：

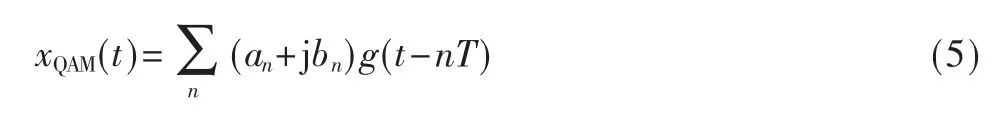
式中，E[an]=E[bn]=0，E[anam]=δ（n-m），E[bnbm]=δ（nm），E[anbn]=0，因此其二次方形式的统计期望可表示为：

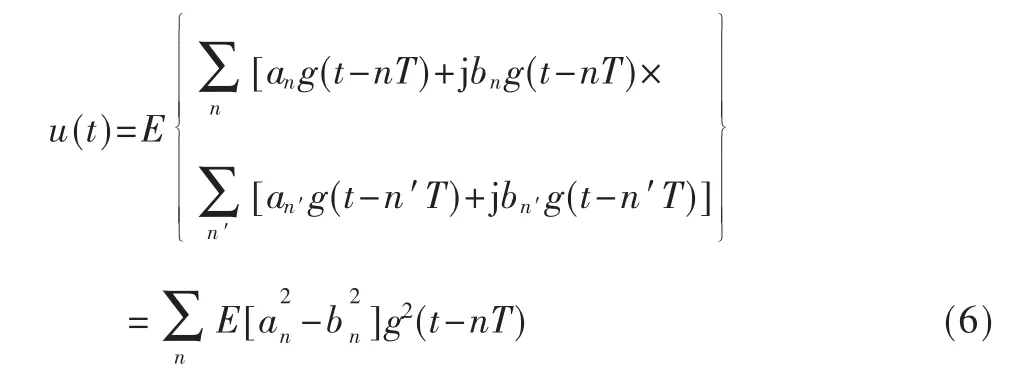
由式（6）可以看出，QAM 信号所对应的二次方谱不存在离散的谱线特征。

对于FBMC 系统其子载波调制采用OQAM 调制，其基带信号表达式为：

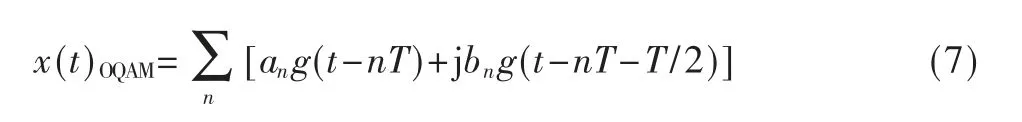
式中，T 表示序列的周期。其二次方形式的统计期望可表示为：

由于E[an]=E[bn]=0，E[anam]=δ（n-m），E[bnbm]=δ（n-m），E[anbn]=0，因此可以得到式（9），如下所示：

从式（9）可以看出ux（t）是周期函数，且其二次方谱可表示为：

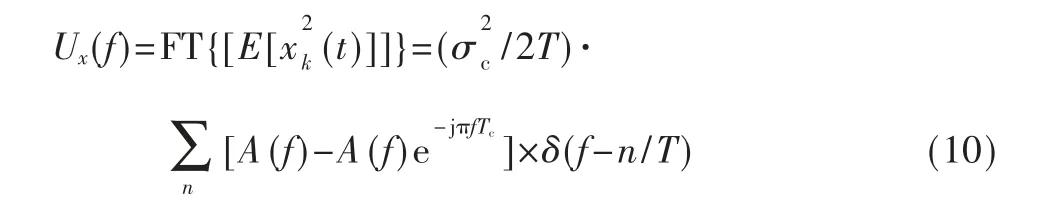
即从式（11）中可以看出，OQAM 信号在f=±1/T 处出现谱线，且信号的幅度可表示为。

2.2 FBMC/OFDM 信号的谱线特征分析

FBMC 复基带信号s（t）的二次方谱与傅里叶变换的性质相结合可以得到：

由式（12）与式（13）可以得到FBMC 信号的二次方谱，表示为：

由此可以得出，FBMC 的二次方谱在f=k/Ts±1/Tc处是离散的，其中，式（14）中ej（π/2）k∈{±1，±j}，因此可以看出离散谱线的个数会随着k 的增加而增加。

而对于QAM 信号而言，由式（6）可以得到，其信号的二次方谱是不存在离散谱线的。但由于OFDM 的时变自相关函数是由所有子载波的时变自相关函数所组成的，由此可以得到式（15）：

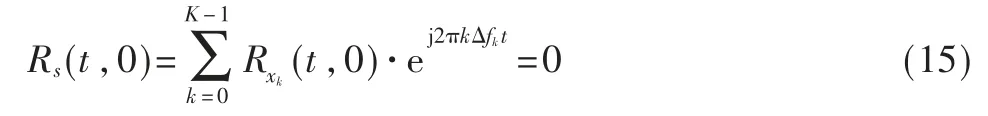
即可以得出，OFDM 信号的二次方谱不存在离散谱线。

3 调制识别方法

由文献[22]可得，离散谱线表示为：

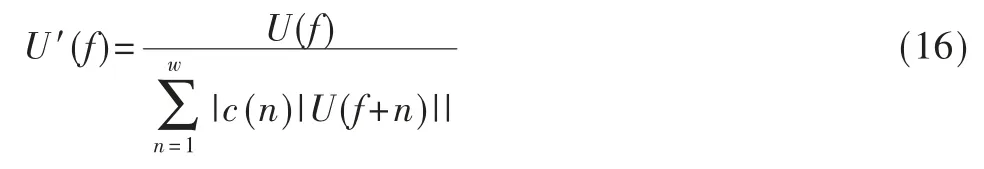
其中，w 为求加权平均值的数据长度，w＜＜L；c（n）为加权系数，满足式（17）：

经过预处理后得到新的二次方谱U′（f），新的二次方谱不仅保留了原有谱线的特征，同时对信号频谱进行了平滑处理，因此可以更好地突出谱线分量。

4 仿真分析

为了验证上述理论分析的正确性，本文完成了以下仿真工作：（1）对多载波调制信号和其子载波的调制信号的二次方谱进行了仿真分析；（2）对经过二次方谱处理及预处理后的子载波数分别为1、2、4 的FBMC 信号的二次方谱进行了仿真分析；（3）对在高斯噪声下不同信噪比条件下OFDM/FBMC 调制方式的正确识别率进行了仿真分析。仿真参数如表1 所示。

表1 OFDM/FBMC 调制信号的仿真参数

图1（a）、（b）分别表示QAM 信号和OQAM 信号的二次方谱，从中可以看出没有产生离散谱线。图2（a）中没有离散谱线，其与理论相吻合。在图2（b）中，当k 的值为1 时，可看作常规OQAM；在图2（c）中，当k 的值为2 时，其二次方谱出现4 个谱峰；图2（d）中，当k 的值为4 时，其二次方谱出现8 个谱峰。即仿真验证了上述理论分析的准确性。

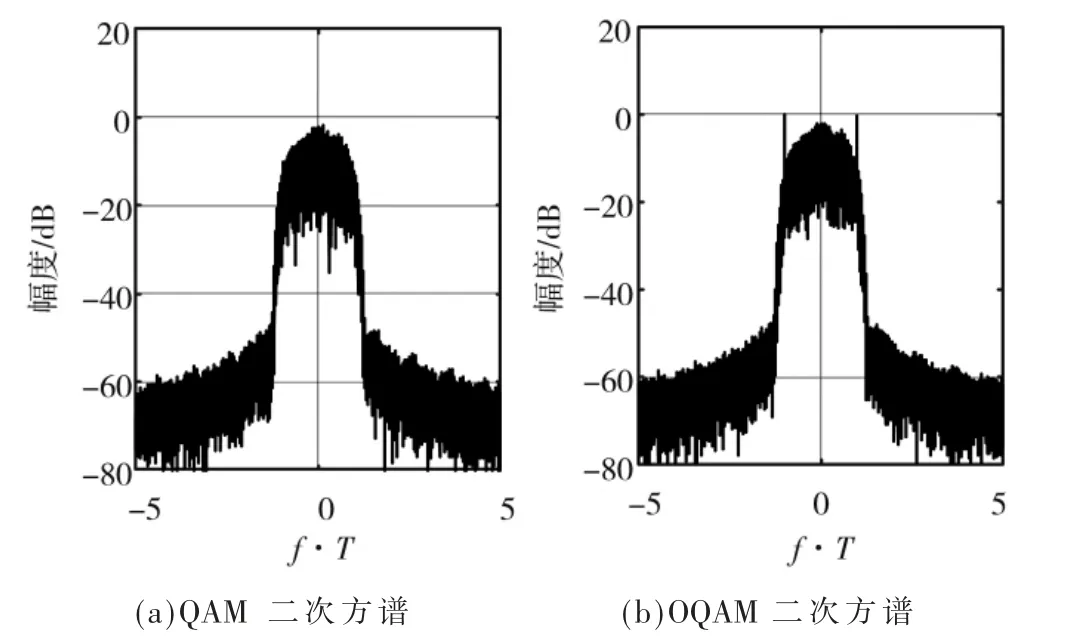
图1 QAM 和OQAM 的二次方谱

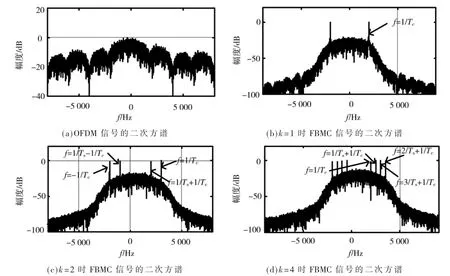
图2 OFDM 信号的二次方谱图和k=1，2，4 时的FBMC 信号的二次方谱图

图3 中（a）、（b）分别为有噪声和抑制噪声后的FBMC信号的二次方谱。

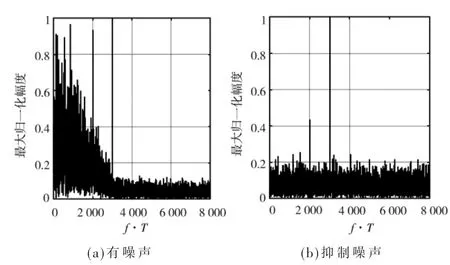
图3 有噪声与抑制噪声后的FBMC 信号的二次方谱

图4 为高斯噪声下不同信噪比下OFDM/FBMC 信号识别率。用谱线提取正确率Pr来衡量信号识别正确率，表示为：

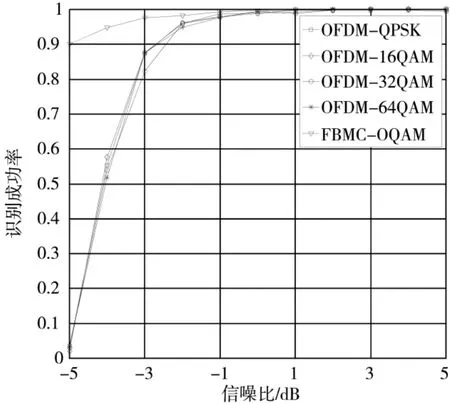
图4 高斯噪声下不同信噪比下OFDM/FBMC 信号识别率

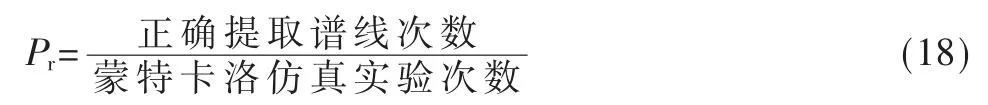
根据图4 可以得到，在信噪比等于0 dB 时，其信号识别成功率大都高于99%。因此可以得出，所提方案可有效地完成对OFDM 信号与FBMC 信号的调制识别分类。

5 结论

本文首先根据各种二次方谱线特征对多载波信号进行相应的建模，接着推导出OFDM/FBMC 信号的二次方谱表达式，最后在高斯噪声下对OFDM/FBMC 进行调制识别。仿真结果表明，所提方案可以很好地对OFDM/FBMC 进行调制识别，为未来通信对物理层波形的使用及分配提供了便利。