用于SoC 电源噪声测量的低温漂VCO*

翟鹏飞 ，周 雄 ，李 强 ，2

（1.电子科技大学 电子科学与工程学院，四川 成都 610054；2.琶洲实验室-人工智能与数字经济广东省实验室，广东 广州 510330）

0 引言

在现代片上系统（SoC）中，电源电压噪声（PSN）问题变得越来越严重，尤其是当工艺尺寸不断减小，电源电压不断下降时，甚至会引起使系统功能出错的时序问题[1-6]。为了更好地对芯片进行设计、测试和调试，需要有效且准确地诊断PSN 相关的问题，并对电源网络进行建模[12-15]。

一种在片上测量电源中具有周期平稳特性的宽带噪声的方法是用两个低速模数转换器（ADC）来测量噪声自相关函数，再对自相关函数进行傅里叶变化，得到的频谱就是噪声的功率谱[4，11]。因为电源上的噪声一大部分是与系统的时钟周期相关的，具有周期平稳特性，所以对周期平稳特性噪声测量是很有意义的。低速ADC中的量化器可以采用基于环形压控振荡器（ring VCO）的结构，这种结构使得测量带宽高达20 GHz[5-6]，满足对片上高频噪声的测量需求。

然而ring VCO 的振荡频率对温度很敏感，这个特性降低了在温度变化较大的应用场景下基于ring VCO 结构的量化器的精度。所以在PSN 测量应用中，用一个不随温度变化，只随电源电压变化的VCO 量化器是很有必要的。之前的文献中给出了一些有益的补偿方法：与产生带隙基准电压的原理相似，在文献[12]中，可以通过三极管发射结电压（VBE）的负温度系数来补偿ring VCO延迟单元的温度系数，以在较大的温度范围内保持频率稳定；补偿也可以通过由具有相反温度特性的不同延迟单元组成的环形振荡器来实现[13]；在文献[14]中，由内部VCO 控制的开关电容器的等效电阻与温度补偿的片上电阻器匹配。总之，这些补偿方法取决于仿真的准确性。

本文提出了一种具有两级温度补偿结构的ring VCO量化器。粗略补偿级是利用与绝对温度成正比（PTAT）电流补偿偏置在4.3 GHz 的VCO 频率的负温度系数。精细补偿级通过VCO 复制电路感知温度变化来自适应地调整量化器中使用的VCO 的偏置电流，可以进一步自适应地降低其温漂值。

1 用于SoC 上PSN 测量的ring VCO 量化器

图1 所示为用于在片上测量电源上周期平稳噪声功率谱的系统结构。整个系统由一个时钟发生器、双通道（T 路和τ 路）ring VCO 量化器和自相关函数的计算模块组成。时钟发生器产生两个采样时钟，它们之间的间隔满足自相关操作。然后用低分辨率的ring VCO 量化器对PSN 进行量化。由于低分辨率量化器的一次性量化时间非常短，因此无需采样保持电路。量化精度可以通过多次采样的平均值技术来提高[5]。

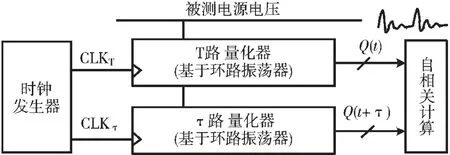
图1 电源噪声测量系统结构框图

1.1 ring VCO 量化器

ring VCO 量化器的电路原理图如图2（a）所示[5]。Ring VCO 量化器中的PMOS 和NMOS 的源极既是控制端口，同时也是供电端口，所以可以把量化器直接放置在被测电源域中。VCO 中每个反相器的输出端同时连接到两个触发器（DFFs）的输入端。采样时钟直接触发DFFs以在固定时间窗TWIN 的起始和结束时刻记录反相器的输出。然后对两个DFFs 的输出进行异或（XOR）运算得到最终的量化结果。

这种量化器主要原理是检测在固定时间窗TWIN 内是否有振荡器的输出波形的上升或下降沿，所以本质上是VCO 输出信号的上升或下降沿检测器。如图2（b）所示，若时间窗内有上升或下降沿，XOR 的结果是“1”；否则XOR 的结果是“0”。上升沿和下降沿出现在TWIN内的概率和VCO 振荡频率成正比。所以多次量化求均值后，得到的结果越大，代表VCO 的振荡频率越快，电源的电压值越高，从而达到对电源电压测量的目的。

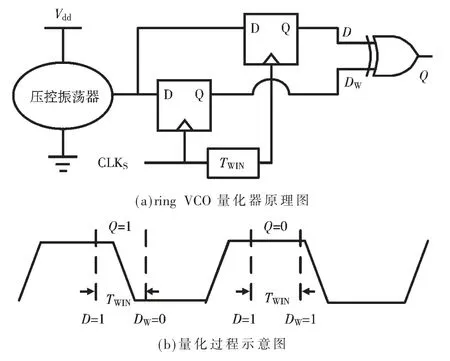
图2 ring VCO 量化器原理

1.2 ring VCO 的温度特性

在电源噪声测量系统中，可以利用ring VCO 量化器尾限流管的栅极控制ring VCO 中流过的电流来补偿振荡频率的温漂曲线。受尾限流管控制的ring VCO 的原理图如图3 所示。ring VCO 的振荡频率与每个延迟单元的延迟时间成反比，延迟时间由每个延迟单元的等效导通电阻和负载电容的乘积（Req-onCload）确定。每个延迟单元的等效导通电阻可以分为两个电阻：上拉和下拉电阻。但需要注意的是这两个电阻不是并联关系而是交替导通的，整个延迟时间是两次导通时间的平均值。所以控制其中一个导通电阻就可以延长或缩短整个延迟时间。

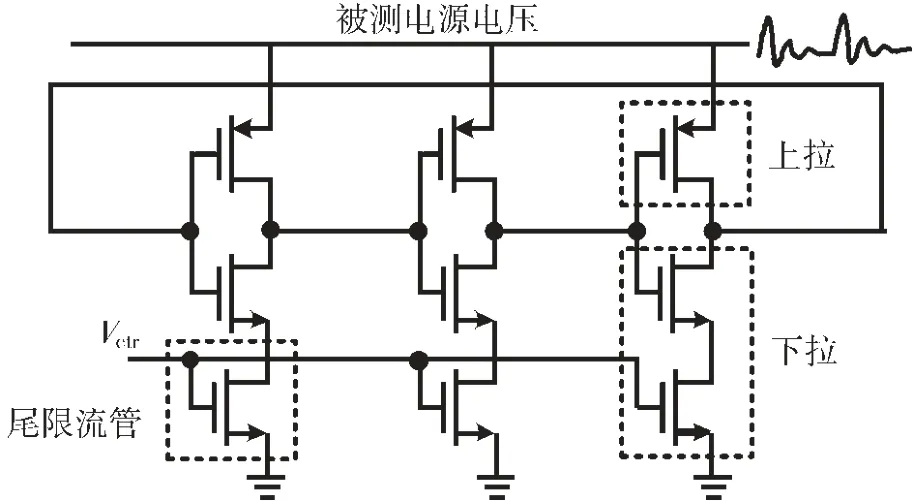
图3 受尾限流管控制的ring VCO 原理图

由于限流NMOS 管的栅极电压低于电源电压，导致其导通电阻大于反相器中NMOS 管的导通电阻，因此延迟单元的等效导通电阻主要由限流NMOS 管决定。在本文中，限流管偏置在深线性区，其等效导通电阻Req-on可以写为：

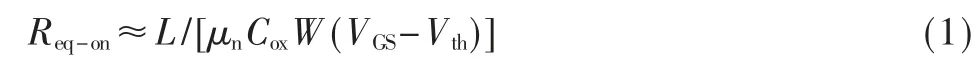
其中L 和W 是NMOS 管栅极的长和宽，μn是载流子的迁移率，Cox是单位面积的栅氧电容，VGS是栅源电压，Vth是阈值电压。如上所述，VCO 的频率与Req-onCload成反比。相对于等效导通电阻的温度系数，可以忽略负载电容器的温度系数。因此，VCO 的振荡频率随温度变化的关系为：

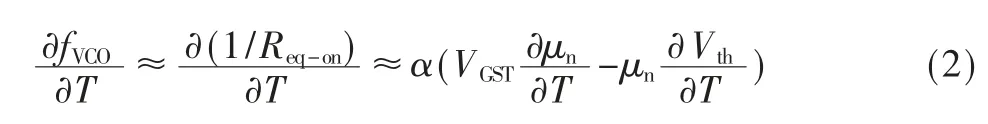
其中fVCO是VCO 的振荡频率，T 是绝对温度，α 是Cox与W/L 的乘积，VGST是过驱动电压。因为μn的温度系数是负，所以第一部分中的∂μn/∂T 为负值；又因为Vth是也是负温度系数，所以第二部分中的-∂Vth/∂T 为正值。由于μn、∂μn/∂T 和-∂Vth/∂T 是由工艺参数决定的，因此对于固定工艺下的电路设计，∂fVCO/∂T 的正负取决于VGST的值，当VGST取值较大时，可以使∂fVCO/∂T 为负值，否则为正值。

图4 中展示的是偏置在深线性区的NMOS 管在不同VGS情况下，偏置电流随温度变化的仿真结果。因为偏置电流的温度系数与Req-on的温度系数是相反的，所以Req-on的温度系数并不是固定值，而是随VGS变化的，当VGS较大时Req-on是正温度系数，随着VGS的减小Req-on的温度系数慢慢变为负值。

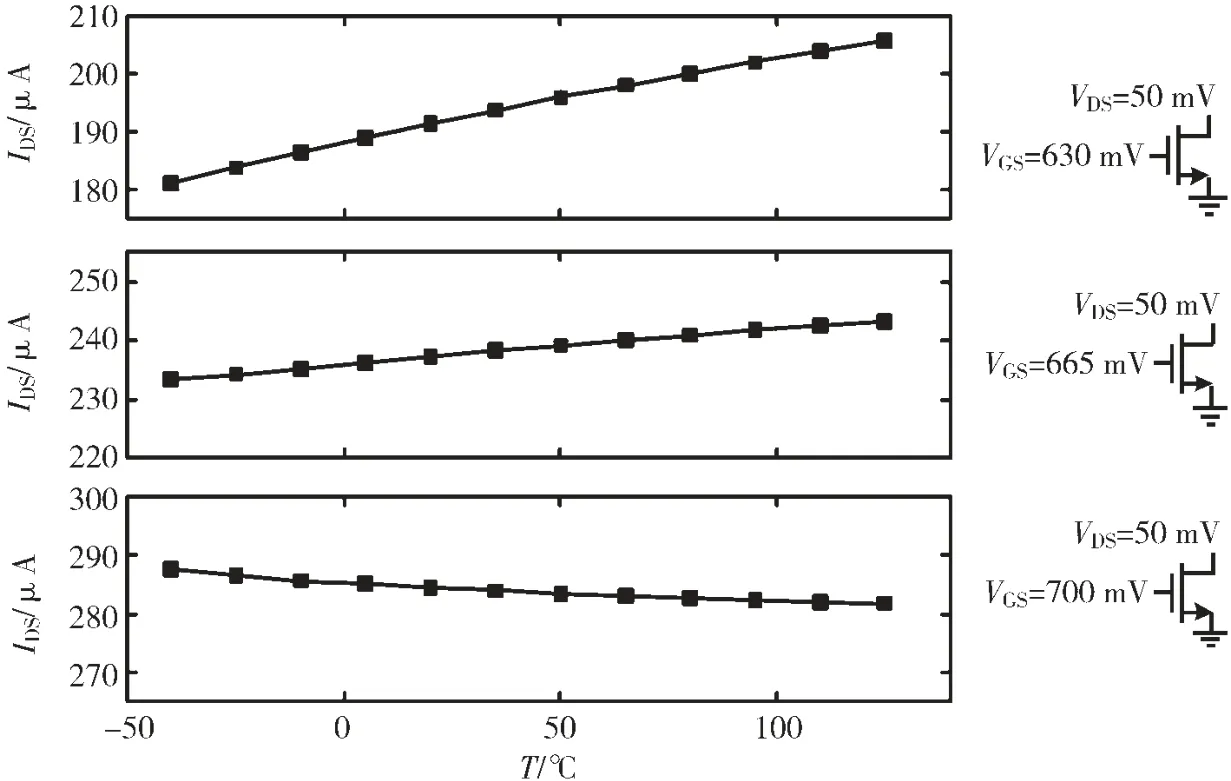
图4 尾限流管的漏极电流在不同VGS 下随温度变化的仿真结果

图5 中展示的是VCO 振荡频率在尾限流管不同VGS的情况下随温度变化的仿真结果。结果表明fVCO的正负温度系数与限流管的VGS有关，且与Req-on温度系数的变化趋势相同。仿真结果与理论分析一致。

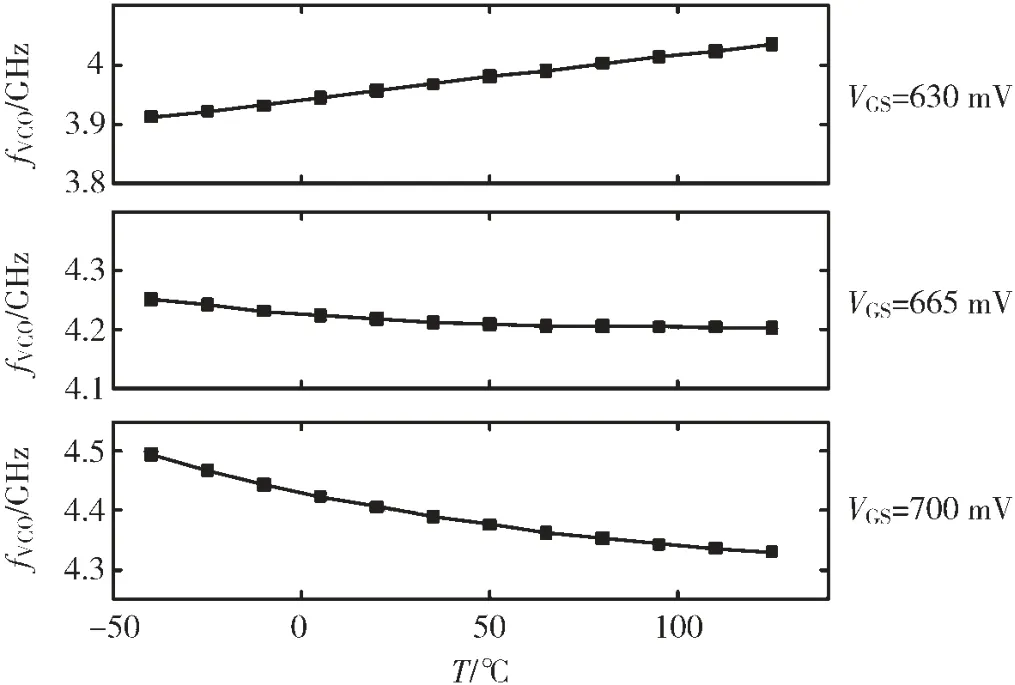
图5 VCO 振荡频率在不同VGS 下随温度变化的仿真结果

2 两级温度补偿电路实现

图6 所示是本文提出的两级温度补偿ring VCO 量化器的结构框图，补偿电路部分包括粗略补偿级和精细补偿级两个部分。粗略补偿级是由用PTAT 电流给ring VCO 的限流管作偏置电流；精细补偿级是由量化器的复制电路感知温度的变化，再反馈给量化器，进一步完成温度补偿。

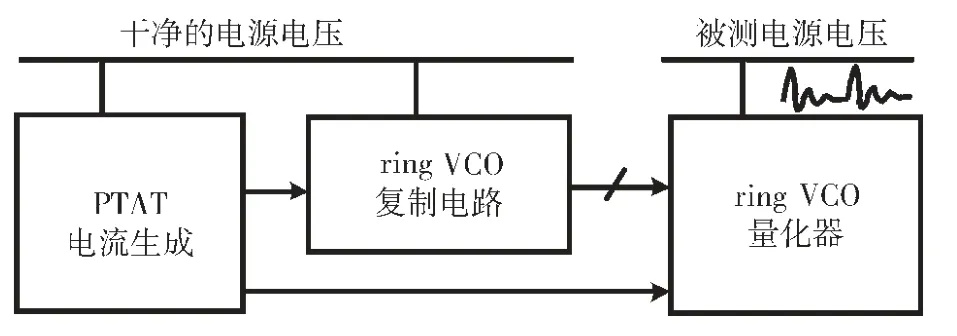
图6 两级温度补偿ring VCO 量化器系统框图

2.1 PTAT 电流产生电路原理图

本文设计的VCO 的中心振荡频率是4.3 GHz，根据图5 所示，此条件下，振荡频率是负温度系数，所以可以设计一个PTAT 的基准电流源为VCO 的限流管提供电流偏置以实现对初步补偿的作用。

图7 所示为PTAT 电流产生电路原理图[15]。由于运放的作用，在理想情况下，使a 和b 两点的电压相同。且Q1 和Q2 的发射极面积比是1：8，所以两个晶体管发射结的电压差ΔVBE为：

图7 PTAT 电流产生电路原理图

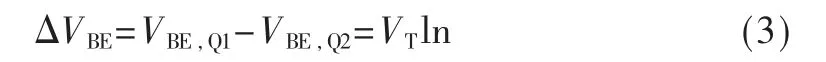
其中VBE，Q1和VBE，Q2分别是Q1 和Q2 的发射结两端电压差，VT是热电压。又因为流过R2和R3的电流和等于流过M2的电流（IM1，2），且R1的电阻值等于R2的电阻值，所以IM1，2为：

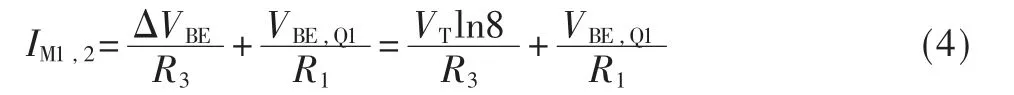
因为VT的电压值和绝对温度成正比，而VBE的电压值随绝对温度升高而下降，所以可以通过调节R3和R1电阻值的比例来调节IM1，2的温度系数。

2.2 精细补偿级原理图

由于VCO 的温度系数并不是完全线性的，如果只用PTAT 电流对VCO 的温度系数进行补偿是不够的。而且芯片的制作过程会有偏差，实际测试的温度系数会和仿真结果有偏差，可能出现过补偿或欠补偿的情况。为了解决这个问题，本文提出一种利用VCO 复制电路感知温度变化，然后再将感知信息传递给VCO 量化器中，使得量化器中VCO 的振荡频率可以在一定范围内对温度变化自适应地调节，得到一个具有更低温漂值的振荡频率。

图8 为精细补偿级电路原理图，其中主要包括量化器中的VCO、用于感知温度变化的VCO 复制电路和反馈信息的逻辑电路三个部分。其中量化器中的VCO 的限流管由两部分组成：一部分是由PTAT 电流偏置；另一部分是由反馈逻辑电路控制。VCO 复制电路中的限流管的偏置电流只由PTAT 电流偏置。

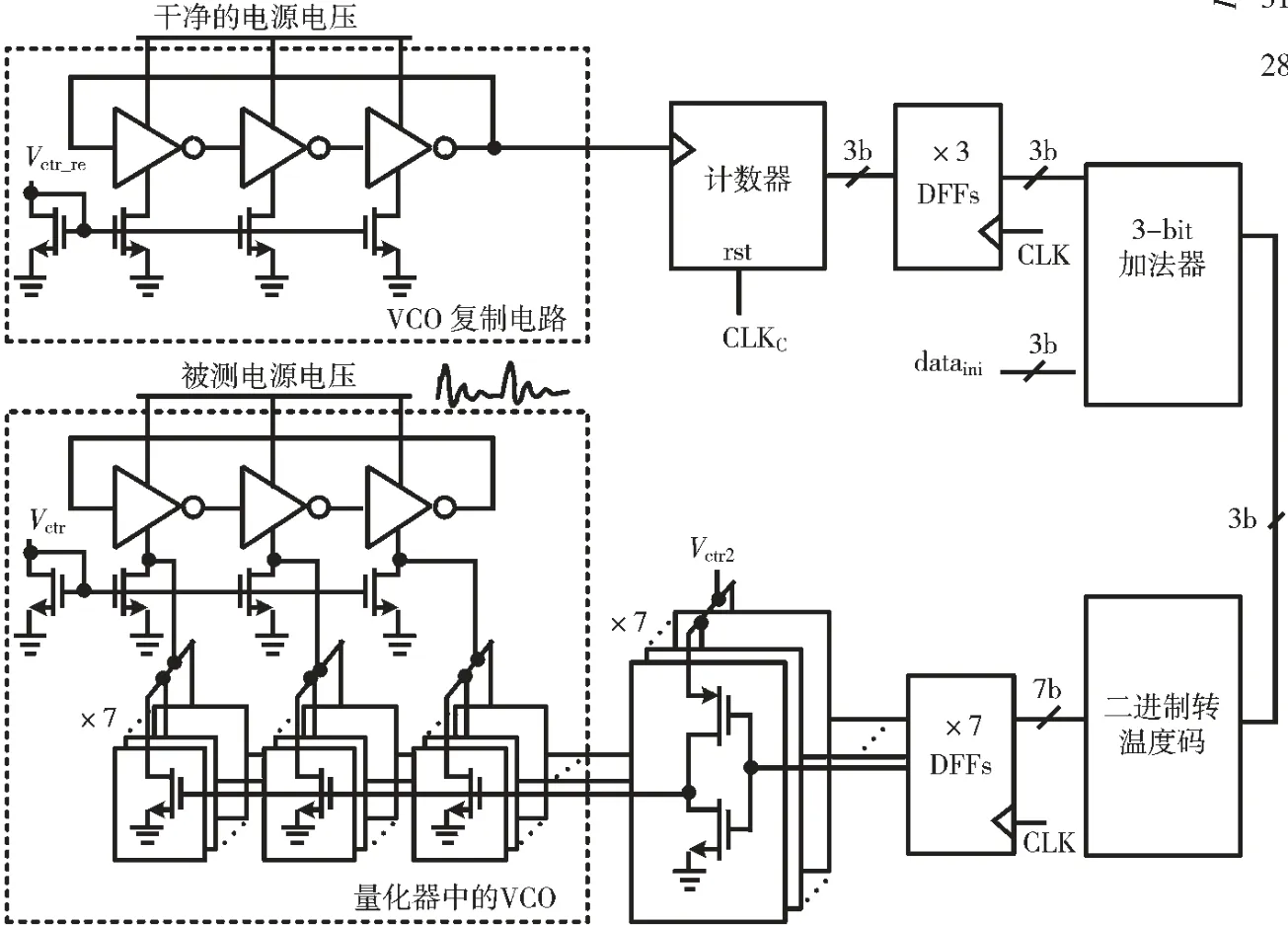
图8 精细温度补偿级电路原理图

此部分电路的工作过程首先是通过计数器在一个固定时钟周期内对VCO 复制电路的振荡频率进行计数。然后将计数结果的低三位输入给3-bit 加法器，与一个初始值dataint相加。这个dataint的作用是为了在常温情况下让加法器的输出为“100”，这样不管温度偏差使频率变快或变慢都有可以自调整的空间。再将加法器3-bit 输出的码字转换成温度码，来控制一个缓冲器阵列，最后缓冲器阵列的输出控制限流管阵列。这种温度补偿的方式并不是连续调节的，而是使VCO 输出频率以最小步长进行调整。这个最小调整步长可以设置为与VCO 复制电路的感知精度相同的值。即可以实现VCO复制电路的频率变化了多少，就可以通过限流管阵列将这个变化从量化器中VCO 的振荡频率中减去，从而保持量化器中VCO 的振荡频率为一个恒定值。VCO 复制电路的感知精度SRES定义为：使计数器变化一个最小码字的频率变化量。所以感知精度与VCO 的中心振荡频率fVCO以及计数时间窗TC有关，计算公式如下：

所以要提高感知精度只能增加TC的长度。需要注意的是，当提高了感知精度，在整个温度变化范围内，计数器的码字变化范围会变大。为了防止码字溢出，需要相应地增加传递给加法器的码字位数，也要增加缓冲器阵列中缓冲器的数量，以及限流管阵列中限流管的数量。同时为了防止实际应用时与仿真的偏差，可以增加一些冗余量，确保补偿的正确性。

图9 所示为精细补偿级的时钟产生电路和波形图。这部分主要目的是产生一个与计数时钟有相同周期的脉冲信号。这个脉冲信号用于给计数器进行复位。具体实现是将计数时钟进行二分频，再将分频后的时钟经过延迟单元，最后将二分频时钟与其延迟后的时钟信号作异或运算，就得到了所需的脉冲信号。

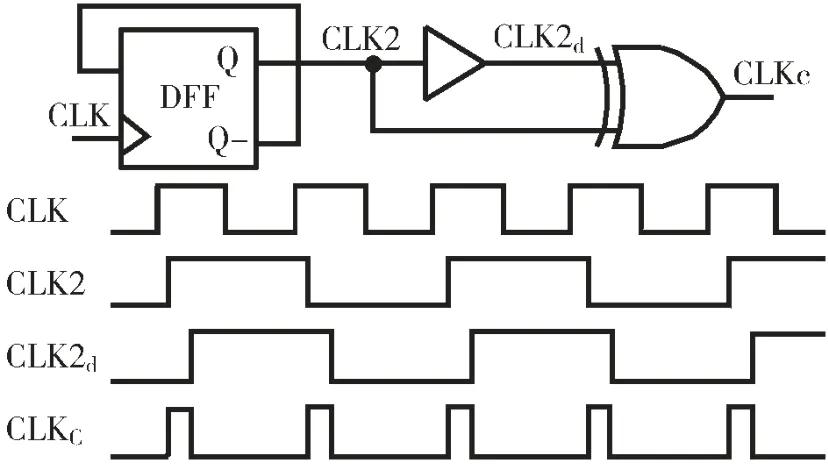
图9 精细温度补偿级时钟产生电路原理图

3 仿真结果

本文提出了使VCO 振荡频率具有低温漂值的两级补偿技术，并在40 nm CMOS 工艺下完成电路设计与仿真，仿真结果如图10～图12 所示。

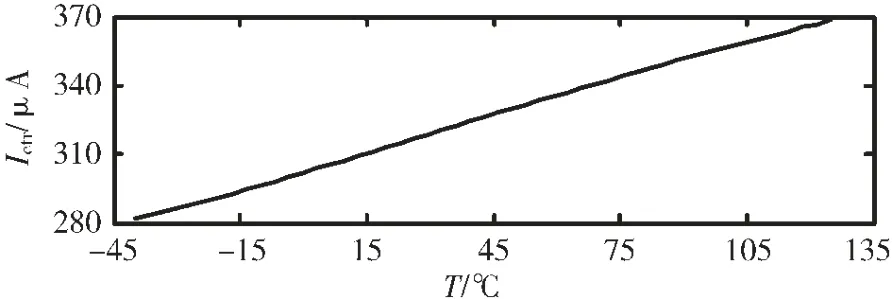
图10 PTAT 偏置电流仿真结果

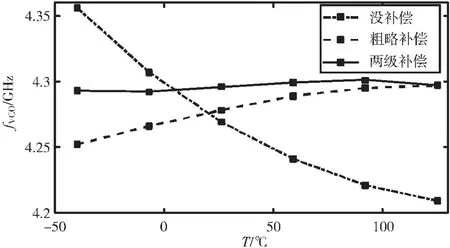
图11 VCO 振荡频率随温度变化的仿真结果

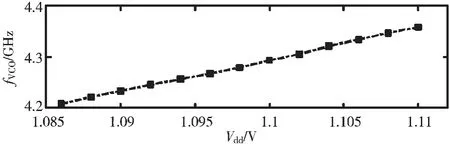
图12 VCO 振荡频率随电源电压变化的仿真结果

图10 为基准电流源产生的PTAT 电流的仿真结果。电流值随温度的升高而变大，这个PTAT 偏置电流补偿一部分VCO 振荡频率的负温度系数。

图11 所示为VCO 振荡频率在没有补偿、只有粗略补偿级以及两级补偿级三种情况下随温度变化的仿真结果。可以看出在没有补偿的情况下，VCO 的振荡频率和温度的关系并不是线性变化的，所以只通过PTAT 电流补偿，温漂值依然较大。在经过第二级的精细自适应补偿之后，温漂值得到进一步缩小。由于第二级补偿是一种离散的补偿方法，在-40 ℃时开启了6 个补偿的尾限流管，可以从仿真结果中看出每个限流管可以提供约7 MHz 的频率补偿。VCO 的振荡频率温漂Tcoe计算公式为：

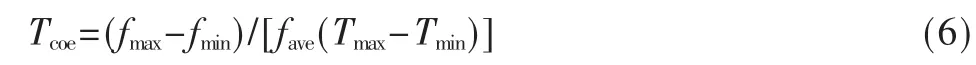
其中fmax是VCO 的最大振荡频率，fmin是VCO 的最小振荡频率，fave是VCO 的平均振荡频率，Tmax是最高温度，Tmin是最低温度。经过计算得到三种情况下VCO 振荡频率的温漂值分别为：208.0 ppm/℃，63.8 ppm/℃，15.5 ppm/℃。

图12 所示为VCO 振荡频率随电源电压变化的仿真结果。结合图11 可以看出，当没有温度补偿时，VCO 随温度的变化范围可以等效为电源电压变化约24 mV，经过一级补偿后等效为电源电压变化7 mV，经过两级补偿后等效为电源电压变化2 mV。也就是说，如果芯片内部温度有较大变化，两级温度补偿结构的VCO 量化器可以较大地提高测量精度。

4 结论

本文介绍了适用于在片上对SoC 电源噪声进行测量的VCO 量化器，对VCO 的温度系数进行了分析，并提出了低温漂VCO 量化器的两级补偿结构。本文基于40 nm CMOS 工艺，对提出的两级补偿结构进行了仿真验证。结果表明两级补偿结构的温漂值比一级补偿的降低了约4.1 倍，比没有补偿的降低约13.4 倍，可以有效提高量化器在温度变化较大的系统中的测量精度。