基于异构多处理平台视频编码并行化复杂度与率失真研究

袁三男, 王孟彬, 张艳秋, 陶倩昀

(上海电力大学 电子与信息工程学院, 上海 200090)

近几年,随着视频采集设备技术的进步[1],采集到的视频分辨率从标清逐渐发展到高清和超高清。数据量更大,视频编码要求也越来越高,因此高效视频编码(High Efficiency Video Coding,HEVC)的推出[2],可以更好地解决视频应用的多样化和视频分辨率的高清化。YANG J等人[3]提出了先检测帧间2N×2NPU(Prediction Unit,预测单元),如果运动矢量(Motion Vector,MV)的差值为零且编码块标志位也等于零,则就提前终止编码。文献[3]是用跳过模式作为PU模式的提前终止条件,这种思想与H.264优化[4]类似。文献[5]提出了一种帧内变换,跳过快速帧内模式选择的思想。运用上述快速算法能够使HEVC以损失3%的编码效率获取1.6～2.6倍的编码加速,但其编码复杂度还是很高且造成了某种程度的编码效率损失。为解决复杂度问题,研究人员将目光投向了比CPU计算能力更强的图形处理器(Graphic Processing Unit,GPU)。它在视频编码中主要应用于运动估计处理。CHEN W N等人[6]采用CPU+GPU的多核处理器实现了自下而上式的运动估计,4×4块的绝对差值和(Sum of Absolute Differences,SAD)由详尽的并行搜索计算而来,并且可变大小块的SAD是由4×4块相加而计算得到的。CHENG R等人[7]评估了在GPU中详尽搜索、菱形搜索和四步搜索的性能。文献[8]提出QP(量化参数)的拉格朗日算子,能更好地平衡编码失真度与输出码率,可显著提高编码速度。

基于上述研究,为了满足视频高清实时编码的需要,本文提出了一种基于CPU+GPU的并行编码框架,通过CPU和GPU的协同作用,更好地提高编码速度以及降低时间复杂度。

1 基于CPU+GPU的视频编码并行化设计

1.1 CPU+GPU并行架构

GPU具有高并行结构,在图形数据的处理和复杂算法上拥有比CPU更高的效率。本文采用CPU+GPU的异构多核处理器,其特点是利用CPU处理逻辑运算和任务调度,将高并行计算任务迁移到 GPU 上处理,解决了CPU和GPU间的任务调配问题,以最大限度提高视频编码效率。

基于异构多处理平台视频编码框架如图1所示。其采用两级并行的方式:第一级并行是CPU和GPU的并行,第二级并行是多核CPU中的多流水线并行[9]。除运动估计过程在GPU上执行外,视频编码其他进程均由CPU执行。同时需要对运动估计过程中的向量选择准则进行修改以实现并行化处理。

图1 基于异构多处理平台视频编码框架

1.2 运动估计

压缩视频的占用空间,提高存储和传输的效率,在获得有效压缩效果的同时,使压缩过程引起的失真最小。这是视频压缩技术的根本目的。运动估计是视频压缩编码的关键技术之一,采用相邻的像素作为参考来预测当前帧的像素,并决定压缩编码速度和效率。

在本文提出的CPU+GPU并行编码架构中,运动估计由GPU负责完成[10],采用全搜索算法和1/4像素精度插值法。具体算法步骤如下。

步骤1 计算8×8块的SAD。在不使用不对称划分(Asymmetric Motion Partition,AMP)工具的情况下,HEVC的PU有64×64,8×4等12种划分模式。为了进一步降低编码复杂度,本文选取8×8块为最小的PU,并以此为基础进行SAD的计算。本文将运动估计搜索范围设定为32×32,因此对于每8×8块有1 024个候选运动向量。

在GPU中并行处理帧宽(WFrame)×帧高(HFrame)的视频所需的线程块数量为

(1)

式中:NBlock——线程块数量;

RSearch——搜索区间。

为提高线程的执行效率并减少处理时间,降低内存访问次数是必要的。为此,在线程块计算同一个8×8块的SAD之前,将编码块从纹理存储器读入线程块的共享内存中。处理每个8×8编码块需用322/256=4个线程块。处理完一帧图像后,全部的8×8块的SAD被保存到GPU的global memory中,以供后续处理。

步骤2 计算其他尺寸块的SAD。计算出8×8块的SAD之后,其他相对较大尺寸块可以由相应的8×8块的SAD相加得到。如8×16块的SAD可以由其对应的两个8×8块的SAD相加得到。在线程设计方面,同一个编码树单元(Coding Tree Unit,CTU)的其他105个SAD用同一个线程进行计算。本步骤设计256个线程/线程块,所需的线程块数量为

(2)

步骤3 选择最佳整像素运动矢量。可变大小块生成完成之后,每个块对应1024个SAD值,最小的SAD对应的整像素运动矢量(Integer-Pixel Motion Vector,IMV)就是最佳的IMV。本文采用一个线程块处理1024个SAD,首先,给线程块中256个线程每个分配4个SAD,并算出最小的SAD及对应的MV。为实现快速存取,将得出的256个SAD及MV存入shared memory中。然后,给256个SAD值分配128个线程,每个线程比较2个SAD,将获得的64个SAD及MV存入shared memory中,依次迭代计算8次,最后得出最小的SAD及其对应的MV,并将它们存入global memory中。

步骤4 分数像素插值及运动估计。对步骤3中计算出的每个块最小SAD的预测块进行插值及分数像素运动估计,并将最后得到的最佳分数像素SAD及分数像素运动矢量(Fractional-pixel Motion Vector,FMV)保存在global memory中。

经上述过程在GPU中处理完一帧视频并将每种块的最小SAD及其对应MV传送到CPU内存中,最后在CPU中用波前并行处理(Wavefront Parallel Processing,WPP)找出CTU最佳的划分模式。

2 GPU中低复杂度快速搜索算法及率失真优化问题研究

目前视频编码针对GPU设计的运动估计几乎都是全搜索算法[11]。全搜索算法尽管能够找到最佳的划分形式,但需要遍历所有的划分,计算复杂度很高,从而使运动估计过程消耗大量时间。因此,对于实现实时编码,降低GPU中运动估计十分必要。

率失真优化技术是提高编码效率的有效手段[12]。它在提高编码效率的同时不受编码结构和技术的限制。无论从信息论还是系统设计的角度,率失真优化技术贯穿了整个视频编码系统。

受TZSearch快速搜索算法[13]启示,在GPU中也能设计菱形搜索算法以降低计算复杂度,但无法获取预测运动向量(Prediction Motion Vector,PMV),因为PMV是从相邻的CTU运动预测中得到的MV,而在GPU运动估计中相邻的CTU处理是同时并行处理的,无法从相邻CTU获取相应的PMV,因而无法使用率失真优化技术选择最佳的CTU划分模式,导致率失真性能下降。因此,找出PMV是在GPU中解决率失真优化问题的关键[14]。

由于CPU具备很强的通用性,所以可以解决各种不同的数据类型,但逻辑判断又会引入大量的分支跳转和中断处理,使得CPU的内部构造异常复杂。GPU面对的则是类型高度统一、相互不依赖的大规模数据和不需要被打断的纯净的计算环境,使得GPU不能像CPU那样具有高效的逻辑判断性能,所以在GPU中很难实现与TZSearch一样具有大量逻辑判断的几步搜索算法[15],即使能实现也会花费大量的时间。这与本文降低计算复杂度以及提升编码速度的初衷相背,因此GPU中的快速搜索算法[16]不能完全采用TZSearch快速算法,必须进行一定的修改。

本文设计的率失真优化快速搜索算法过程如下。

2.1 64×64 PU搜索

运动矢量预测(Motion Vector Prediction,MVP)为运动估计指定了一个中心位置,在这个中心位置适度的范围内能找到最佳预测块。为了防止缺少MVP造成编码效率的损失,使运动搜索可以找到更好的中心位置,本文提出了一个针对64×64 CTU的整数搜索方案。在搜索过程中,搜索范围为32×32。

每个CTU第一步是采用69点菱形搜索模式,用式(3)确定搜索位置,即

(3)

式中:D——搜索点距离中心点的位置。

D≤16时菱形搜索模式如图1所示。

第二步是以第一步最佳搜索点作为中心点,在13×13范围内实施全搜索。

图2 菱形搜索模式(D≤16)

在搜索算法中,为了方便计算出每个搜索位置的64×64 CTU的SAD,在运动估计时,率先计算出一帧高清视频中所有8×8块在32×32范围内的所有SAD,并将其存入global memory中。

1 920×1 088(填充8行)的高清视频由510个64×64 CTU组成,每个CTU搜索69个位置,需要计算出69个SAD,因而在GPU Kernel中分配了510个线程块,每个线程块分配了69个线程计算相应的SAD,存入global memory中。

对上述计算出的69个点的CTU SAD进行了比较,找出率失真性能最小的SAD以及最佳MV。由于此时没有PMV存在,则可以设其值为零,选择出的最优位置就变成选择最小的SAD。首先创建一个32条流水线的线程块,其中的前5条流水线可以计算出3个SAD,剩下的流水线也能每个再计算2个SAD。为了提升存取的速度,将得到的32个SAD存入Shared memory。然后创建一个包含16条流水线的线程块对比32个SAD,并且将16个SAD 存入Shared memory,依次迭代5次直到计算完。最后得到的最小值SAD对应的MV,保存到global memory中。

然后,以第一步取得最小SAD的位置为中心点进行169点全搜索,并且以第一步获得的MV作为PMV。为便于计算出率失真代价并提高计算速度,将提前计算的MV比特表存入GPU的Constant memory,需要计算率失真代价时,根据相应的MV查表就可以得到运动向量的比特。

计算169点64×64 CTU SAD与第一步相似,只是将线程块的69条线程改为169条线程,但找出最佳位置不再是单纯地比较169点的SAD,而是通过计算出率失真代价来选择最佳位置以及最佳MV。率失真代价计算公式为

J=SAD+λRDMV

(4)

式中:SAD——绝对差值和;

λ——拉格朗日因子;

R——编码PU所需要的码率;

DMV——当前块的真实运动向量和预测运动向量的差值。

具体过程为:首选创建具有169条流水线的线程块,并用式(4)将MV,PMV,SAD对应的率失真代价计算出来,存入shared memory,再用迭代算法计算最小代价,将最小代价及其对应的SAD以及MV都存进global memory中。

2.2 其他PU的搜索

运动估计过程中子块的运动趋势往往与其对应的母块运动趋势一致,并且子块最佳匹配位置一般距离母块最佳匹配位置很近,所以子块选母块的最佳MV作为PMV,同时以母块取得最佳MV位置作为起始点。

其他 PU两步搜索方案中,第一步是采用81点菱形搜索模式,确定搜索位置的公式为

(5)

第二步是以第一步最佳搜索点作为中心点,在9×9的范围内实施全搜索。

此计算过程和上一节类似,这里不再详述。

2.3 分数像素搜索

进行分数像素搜索前必须进行插值,首先进行1/2插值,创建的每个线程完成3个1/2像素插值,并将插值完成的图像保存到global memory中。然后对1/2插值图像进行1/4插值,并存于global memory中。

完成插值后每个整数像素对应24个分数像素,在每种PU块的整数最佳匹配位置进行24个分数像素位置的SAD计算,然后用全搜索的方式计算各个分数像素位置的率失真代价并选出最佳值。为了高效地选出最佳的分数像素位置,将分数像素SAD计算与率失真代价结合起来在一个线程块内完成。对于一个64×64 CTU共需计算10种PU的分数像素运动估计,故需创建169个线程块,每个线程块创建24个线程计算,每个流水线计算一个分数像素位置的SAD及率失真代价,然后在线程块内进行迭代比较,选出最优分数像素位置,将对应的SAD及MV存入global memory中。

3 实验结果及分析

将HM10.0,x265编码器与本文设计的改进前后的两种编码器相比较。由于CPU的核数有限且针对实时编码,故采用8线程WPP做实验。测试序列选为BasketballDrive_1920x1080_50.yuv 和 Cactus_1920x 1080_50.yuv。Proposed表示本文设计的基于异构多核CPU+GPU处理平台上的并行实时编码算法,Improved表示本文设计的在GPU中基于率失真优化的快速搜索算法,实验结果如表1和表2所示。其中,PSNR为峰值信噪比。由表1和表2可知:在GPU中基于率失真优化的快速搜索算法以牺牲很低的率失真为代价,在一定程度上加速了视频编码过程,使得编码速度比其他HEVC编码器更接近高清视频实时编码的要求,如BasketballDrive序列最快编码速度从28.63 fps增长为35.22 fps。

表1 BasketballDrive序列在不同编码器中的实验结果

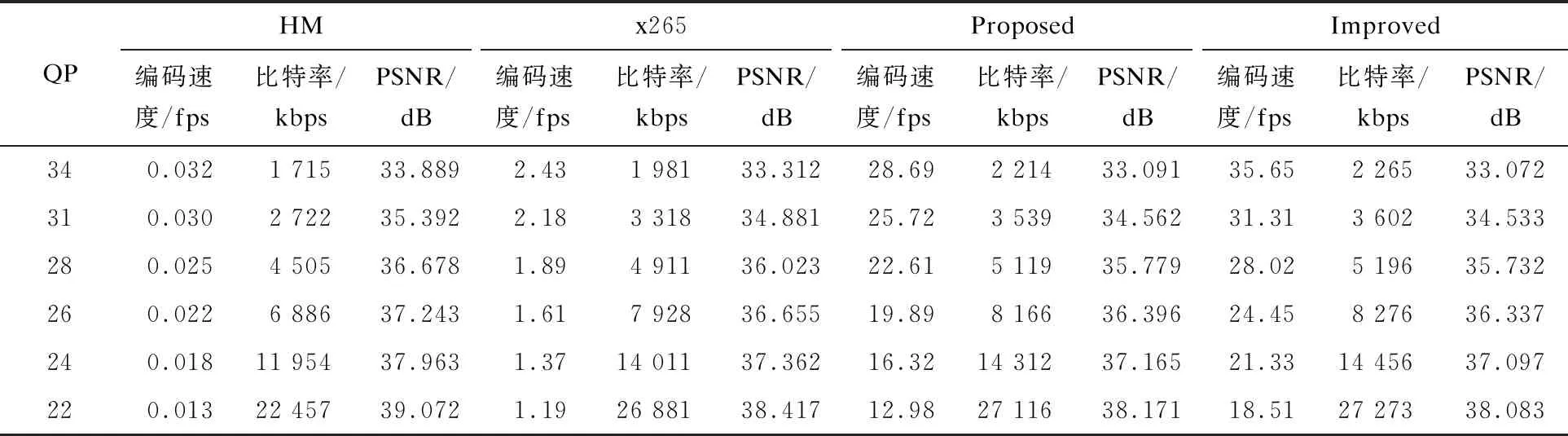
表2 Cactus序列在不同编码器中的实验结果

BNasketballDrive和Cactus序列在不同编码器中率失真曲线如图3和图4所示。由图3和图4可知:本文设计的在GPU中基于率失真优化的快速搜索算法运动估计的率失真曲线与另外3种全搜索算法中性能最好的一条率失真曲线基本重合,并且编码速度进一步加快。

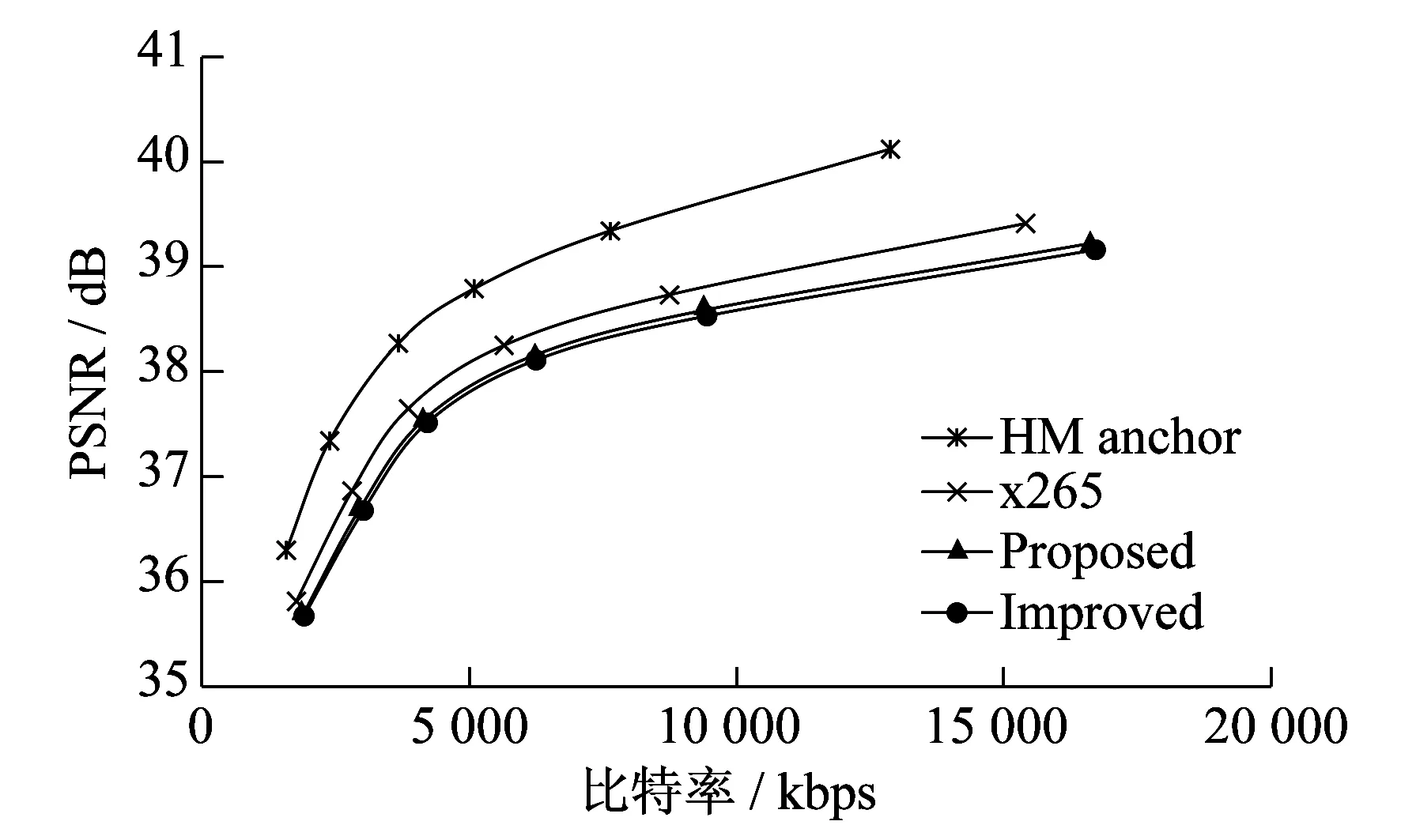
图3 不同编码器编码BasketballDrive的率失真曲线

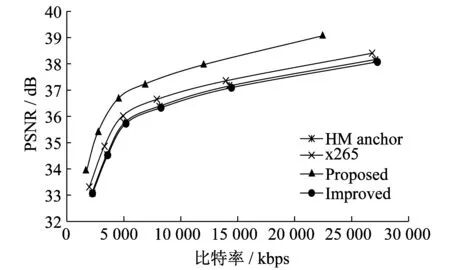
图4 不同编码器编码Cactus的率失真曲线

4 结 语

本文受TZSearch快速搜索算法的启发,提出了一种在GPU中基于率失真优化的快速搜索算法,并在异构多核处理平台上对CPU+GPU的协同处理进行了优化,在不牺牲率失真性能的前提下,一定程度上提升了视频编码速度并进一步接近了实时编码的要求,如将BasketballDrive和Cactus序列的编码速度从28 fps提到了35 fps,同时也降低了计算复杂度。