制冷剂R1336mzz(E)液相黏度理论与实验研究
2021-06-30许晨怡叶恭然郭豪文庄园郭智恺韩晓红陈光明
许晨怡,叶恭然,郭豪文,庄园,郭智恺,韩晓红,陈光明
(1浙江省制冷与低温重点实验室,浙江大学制冷与低温研究所,浙江杭州310027;2含氟温室气体替代及控制处理国家重点实验室,浙江省化工研究院有限公司,浙江杭州310023)
引 言
环境问题是发展中必须重视的问题,目前对日益突出的环境问题的解决办法主要有两种方向:减少对环境的污染与破坏,以及提高能源的使用效率。制冷系统自问世以来,在建筑、食品、药品、运输等工业领域发挥了十分重要的作用;而另一方面,作为制冷系统的“血液”,制冷剂是造成臭氧层破坏与温室效应的重要原因。随着人们对环境与气候问题的日益关注,在一系列国际公约的推动下,制冷剂的选择向环保、高效的方向发展,其发展历程如表1所示。2016年11月生效的《巴黎协定》对全球变暖潜值(GWP)高的产品加强管控,旨在把全球平均气温升幅控制在工业化前水平之上2℃以内[1]。《蒙特利尔议定书》基加利修正案于2019年1月1日正式生效,将一些常用的HFC制冷剂如R245fa(GWP=1030)列入管控范围,预计将减少88%的HFCs排放[2]。在这一背景下,目前制冷行业对新型制冷剂的要求是臭氧层消耗潜值(ODP)为零、全球变暖潜值(GWP)较低、且具有较高的制冷效率,在此背景下有人提出了氢氟烯烃(HFOs)制冷剂[3-4],其被认为具有良好的制冷剂替代前景[5-6]。

表1 制冷剂发展历程Table 1 Development history of refrigerants
提高能源使用效率是近几十年一直处于讨论中的热点内容。回收废热并将其用于热水供应、食品工业中的制冷/制热、干燥/脱水等应用场合是一种有效的解决方案。有机朗肯循环和高温热泵是两种能开发和利用低温余热资源的系统,可以降低能耗和提高工艺效率,减少对化石燃料的依赖性。在目前的应用中,R245fa被认为是最适用于有机朗肯循环与高温热泵的工作流体。但是,如前文所述,R245fa被《蒙特利尔议定书》基加利修正案列为管控范围内的HFC制冷剂,其较高的GWP值对气候问题具有重大影响,将在不久的将来逐步淘汰。在HFO类制冷剂中,R1336mzz(E)的ODP为零、GWP值较低(7.0),大气寿命极短且不可燃、安全无毒(A1),其饱和性质及临界性质与R245fa接近[7],在高温热泵和有机朗肯循环中有希望成为R245fa的替代制冷剂。制冷剂替代工作中,在新型制冷剂环保、安全的前提下,必须进一步研究测量其热物理性质,获得大量可靠的数据并进行充分的评估,才能论证其满足工业应用及系统设计的需要[8]。制冷剂的热力学性质与迁移特性是制冷系统设计和优化的基础[9]。近年来,许多研究人员对R1336mzz(E)的热力学性质进行了研究,并获得了有价值的参考。Raabe[10]对R1336mzz(E)进行分子动力学模拟,通过汽液相平衡模拟预测了R1336mzz(E)的蒸气压与饱和性质。Tanaka等[8,11-12]测量了R1336mzz(E)的临界参数与323~403.37 K温度下的pVT数据并使用Wagner型方程进行关联;测量了323~523 K温度下的pρT数据并使用BWRS方程进行关联。Boonaert等[13]提出使用HFC-HFO混合物来降低HFO制冷剂的可燃性,并测量了R1336mzz(E)与五种HFC/HFO制冷剂二元混合物的汽液相平衡数据。Juhasz等[14]实验验证了R1336mzz(E)在高温下的稳定性和与润滑油及材料的相容性,并研究了R1336mzz(E)与R245fa在高温热泵中的性能系数,结果表明两者的性能系数接近。Yang等[15]研究了R1336mzz(E)、R1234ze(Z)、R1233zd(E)作为R245fa的直接替代品在有机朗肯循环中的适用性,在三种HFO制冷剂中,R1336mzz(E)的循环性能较低(其热效率低于R245fa约5%),这主要是由于R1336mzz(E)的饱和温度较低导致其蒸发温度较低,冷凝温度较高。但目前实验确定的R1336mzz(E)热物性数据仍然有限,在实用化进程当中,仍然需要新的热物性参数进行补充与完善。
黏度作为流体重要的迁移性质,对流体流动中的传热和压降特性有重要影响[16],同时,黏度对温度变化十分敏感,其与温度的变化关系可用黏温特性表征。高温热泵与有机朗肯循环由于热源温度的影响,跨越较大的温区,工作范围内温度变化引起制冷剂黏度的变化,对循环的传热和功率需求产生重要影响。因此,对R1336mzz(E)黏度的研究是其热物理性质中必不可少的一部分。本文采用旋转式毛细管黏度计,在278~333 K温度范围内对制冷剂R1336mzz(E)液相黏度进行实验研究,并根据四种Andrade液体黏度方程对实验数据进行拟合与讨论。
1 实验装置和方法
1.1 黏度测量方法与测量系统
常用的测量流体黏度的装置有毛细管黏度计、旋转式黏度计、落球黏度计、振动式黏度计、孔隙黏度计、超声波黏度计等,不同测量仪器的原理与优缺点如表2所示。毛细管黏度计结构简单,操作简便且精度较高,在制冷剂等工作液的黏度测量中使用广泛,我国现行规范也对毛细管黏度计建立了标准[17-18]。毛细管黏度计一般由玻璃加工而成,制冷剂等工作流体的挥发性较强,在密闭环境中测量黏度时对测量装置的承压能力要求较高。Cousins等[19]和吴江涛等[20]采用不锈钢加工成毛细管黏度计,提高了测量系统的承压能力,并使用曲柄实现黏度计的翻转升液,避免了放气对混合物组分的影响。但黏度装置中不锈钢毛细管的线性度、粗糙度由于受工艺的影响不易加工像玻璃一样的精度,进而影响到黏度测量精度。

表2 黏度测量仪器比较Table 2 Comparison of viscometers
本文采用袁晓蓉等[21-22]基于毛细管黏度计提出的新型黏度测量装置,使用旋转式毛细管黏度计测量黏度,并将翻转升液法与承压容器相结合。玻璃加工而成的毛细管黏度计提高了测量精度,翻转黏度计升液的方法避免了抽吸升液过程对样品纯度的影响,使用承压容器提高了系统的承压能力。
实验装置中最主要的部分是旋转式毛细管黏度计,其结构如图1所示,包括依次连接的上贮液器、计时球、毛细管、悬挂水平球、下贮液器和升液管。悬挂水平球上接有注液管,计时球与上贮液器之间设有与注液管倾斜连接的旁通管。旋转式毛细管黏度计的具体尺寸如下:毛细管长度为160 mm,内径为0.35 mm,计时球和悬挂水平球体积为7500 mm3,上下贮液器体积为15000 mm3。
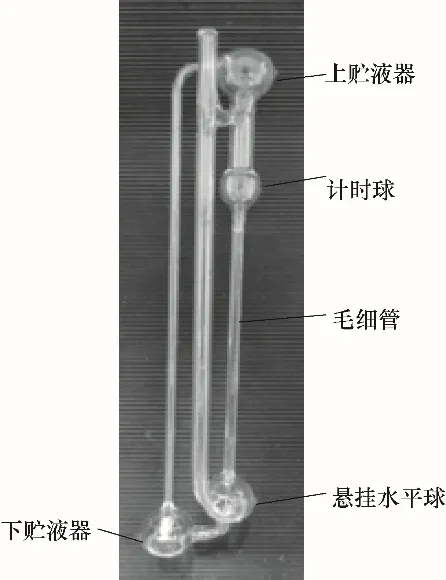
图1 旋转式毛细管黏度计Fig.1 The rotatablecapillary viscometer
整个测量系统如图2所示。压力容器的设计压力为5 MPa,左右两侧各设计了一个直径为40 mm的观察窗以满足实验观察需要。压力容器外带有旋转压力容器的装置,压力容器的翻转通过链条传动实现。受压力容器尺寸的限制,恒温系统采用了一种二次恒温槽的结构,包括为二次恒温槽提供稳定冷源的一次恒温槽,低温恒温循环泵和直接为黏度测量提供稳定环境温度的二次恒温槽。实验过程中,二次恒温槽内的温度波动小于5 mK/min。主要的测量设备仪器型号、量程及精度如表3所示。
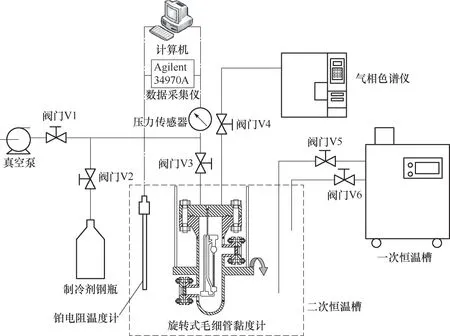
图2 黏度测量系统示意图Fig.2 The schematic layout of viscosity measurement system
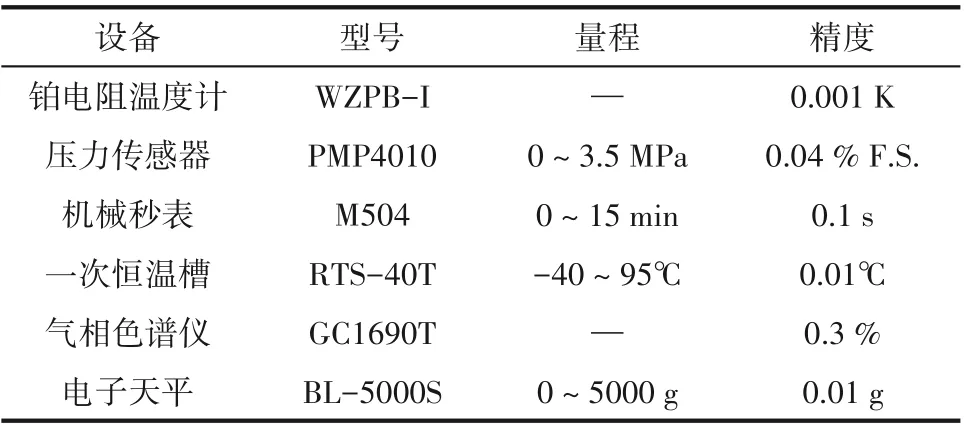
表3 黏度测量系统主要仪器设备Table 3 Main instruments and equipment
1.2 实验装置的标定
黏度由被测液体从上贮液器流过毛细管的时间表征。为了保证测量数据的一致性,流出时间需要反复测量多次,并取其平均值。本次实验采用改进型的Hagen-Poiseuille方程[23],在流出时间与黏度间建立关系式,如式(1)~式(3)所示:


其中,参数α和β仅与毛细管黏度计的结构有关,对同一黏度计为定值,可通过标定得到。
在本次黏度测量过程中,使用纯度为99.9%的R22作为标定工质,在278.15~333.15 K温度范围内进行标定,从REFPROP 10.0获取密度与黏度的参考数据。通过标定得到的关联式最大绝对偏差(MAD)与平均绝对偏差(AAD)分别为1.2%与0.7%,拟合得到α和β的值分别为0.0006594 mm2/s2和2.040 mm2。
1.3 实验不确定度分析
根据式(1)~式(3)进行动力黏度的不确定度分析,如式(4)所示。数据的误差主要源于温度、压力、时间的测量与密度的计算。温度的测量误差源于二次恒温槽温度波动(小于0.01 K)、铂电阻温度计(0.001 K)与数据采集仪(0.005 K),合成后的不确定度为0.011 K。压力的测量误差源于压力传感器(1.4 kPa)与数据采集仪(0.002 kPa),合成后的不确定度为1.4 kPa。时间的测量误差主要源于人工计时的影响,实验测量过程中,时间的最大误差为3.0 s,标定过程中流出时间的最小值为189.4 s,因此时间的最大不确定度为1.58%。密度的误差来源于本文选用PR状态方程[23]和Hankinson-Thomson方程[24]计算饱和密度,模型的最大偏差为0.499%。合成后动力黏度的不确定度约为2.62%(置信系数k=2)。

2 实验结果与讨论
2.1 R1336mzz(E)的基本热物性
目前已公开的R1336mzz(E)热物性研究中,Tanaka等[7]对其基本热物性进行了实验测量,所得R1336mzz(E)的基本特性如表4所示。
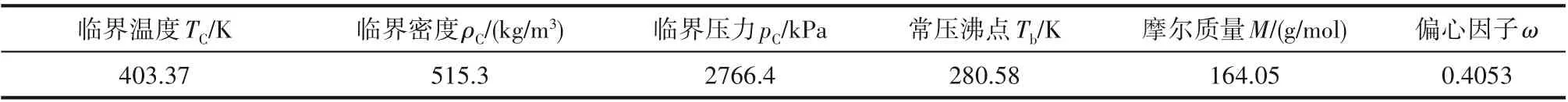
表4 R1336mzz(E)的基本热物性[7]Table 4 Fundamental characteristic properties of R1336mzz(E)[7]
毛细管法测量液相黏度需要准确的密度数据,本文研究中采用的密度数据计算如下。R1336mzz(E)的饱和蒸气压ps由Tanaka等[7]实验拟合的式(5)计算,饱和液相密度ρL与饱和气相密度ρV分别使用式(6)表示的PR状态方程[23]和式(7)表示的Hankinson-Thomson方程[24]计算。不同温度下对应的R1336mzz(E)饱和密度数据如表5所示。
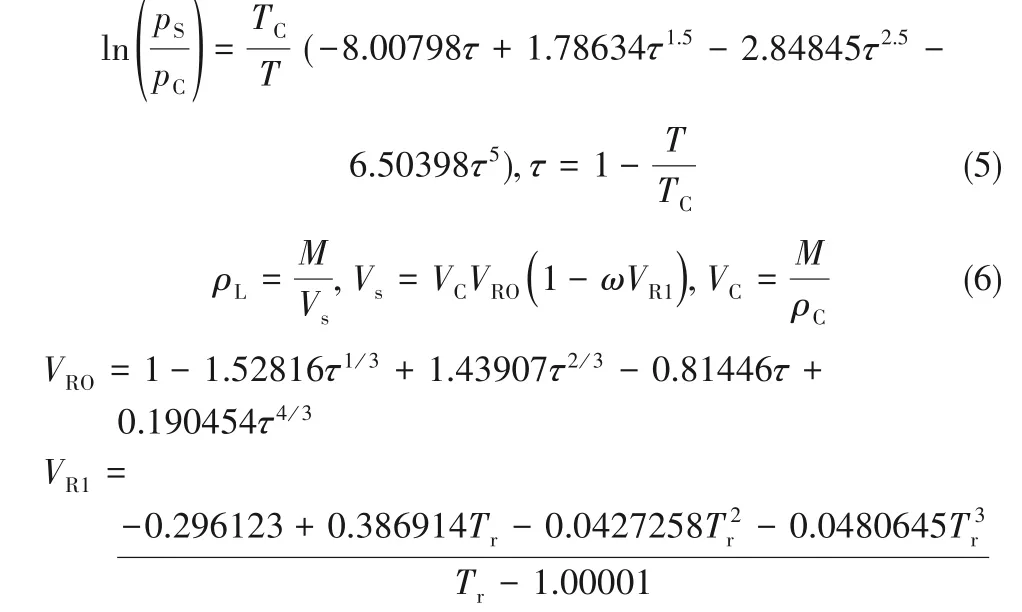
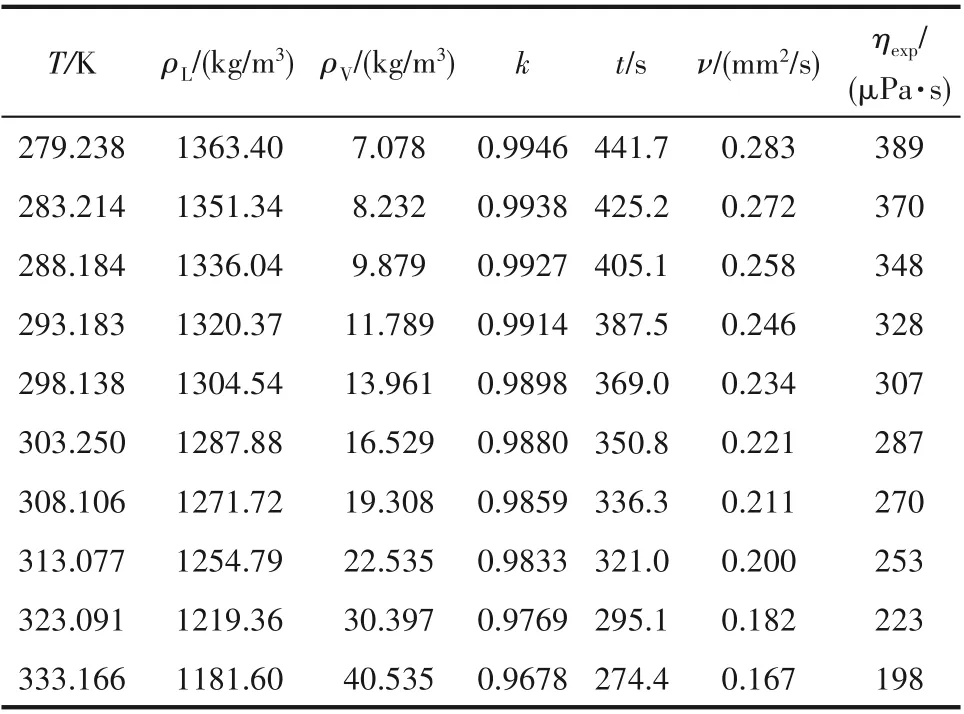
表5 R1336mzz(E)的液相黏度测量结果Table 5 Experimental data of the liquid viscosity of R1336mzz(E)
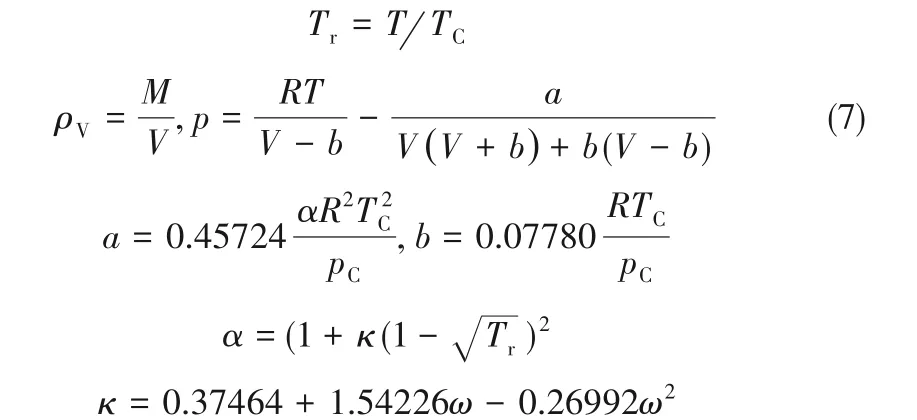
2.2 黏度测量结果与讨论
本次实验测量了278~333 K温度范围内制冷剂R1336mzz(E)的液相黏度,实验结果如表5和图3所示。实验测量得到的黏度是R1336mzz(E)的运动黏度ν,为方便工程应用,本文计算了R1336mzz(E)的动力黏度η作为其液相黏度,并在此基础上建立制冷剂R1336mzz(E)的液相黏度与温度的关联式。
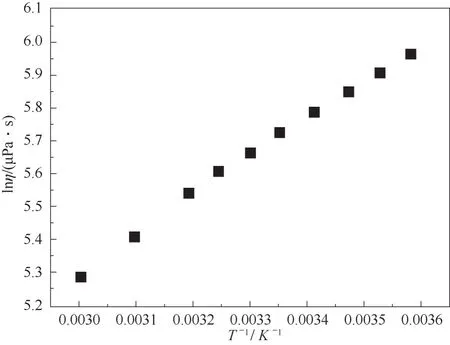
图3 R1336mzz(E)黏度随温度变化散点图Fig.3 Scatter plots of the temperature dependence of viscosity of R1336mzz(E)
最简单的表示液体黏度对温度变化的关系式(8)通常被称为Andrade方程[25]。Andrade方程可以转化为式(9)所示的对数形式,其中A1、B1是待拟合的参数。
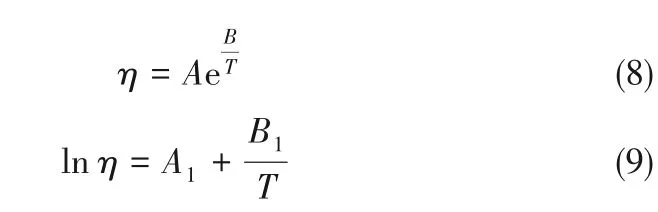
Andrade方程中lnη与1/T呈线性关系,适用于非极性流体。对于极性流体,Girifalco[26]在Andrade方程的基础上加入非线性修正,加强描述极性流体黏度的能力,形式如式(10)所示,式中A2、B2、C2为待拟合的参数。
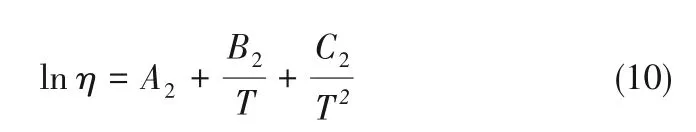
Yaws等[27]提出了一种适用于凝固点至临界温度范围的关联式,如式(11)所示,式中A3、B3、C3、D3为待拟合的参数。

Viswanath等[25]提出了一种与Antoine方程形式相似的关联式描述黏度与温度的关系,如式(12)所示,式中A4、B4、C4为待拟合的参数。
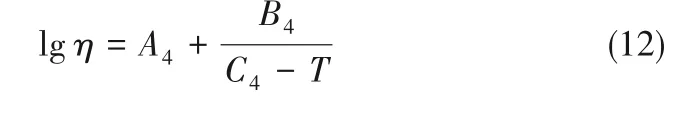
将上述四种模型与表5中的实验数据进行拟合,最终得到黏度关联式的拟合参数和拟合偏差如表6、表7和图4所示。可以看出,式(10)的精度最高,式(11)的精度与其接近,两者的精度优于式(9)和式(12),四种模型的偏差都在实验不确定度范围之内。
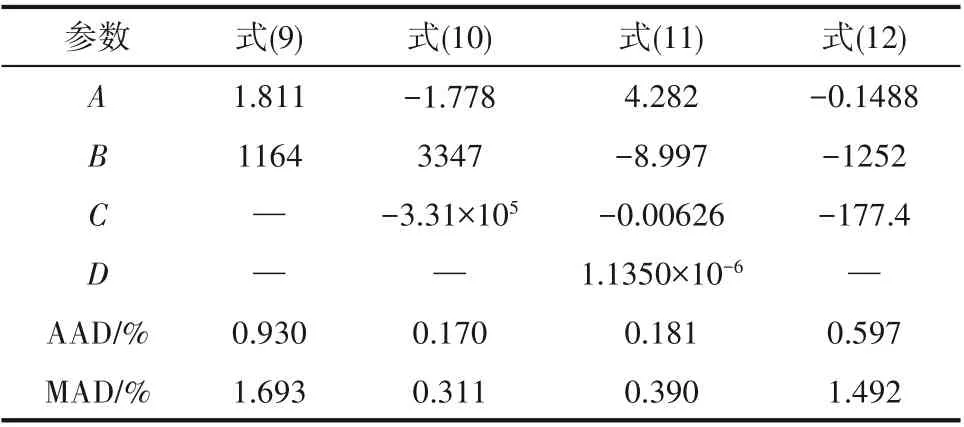
表6 四种模型的拟合参数和拟合偏差Table 6 The correlation parameters,AAD and MAD of four viscosity models
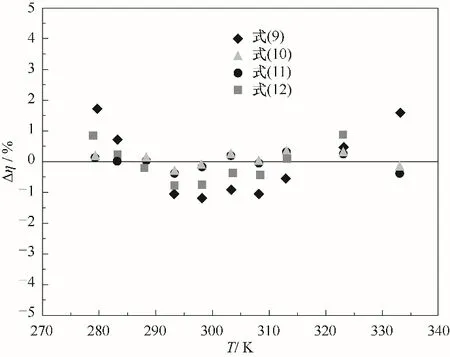
图4 四种模型关联方程与实验数据的偏差Fig.4 Deviations for R1336mzz(E)of the correlation of four viscosity models fromthe experimental viscosity
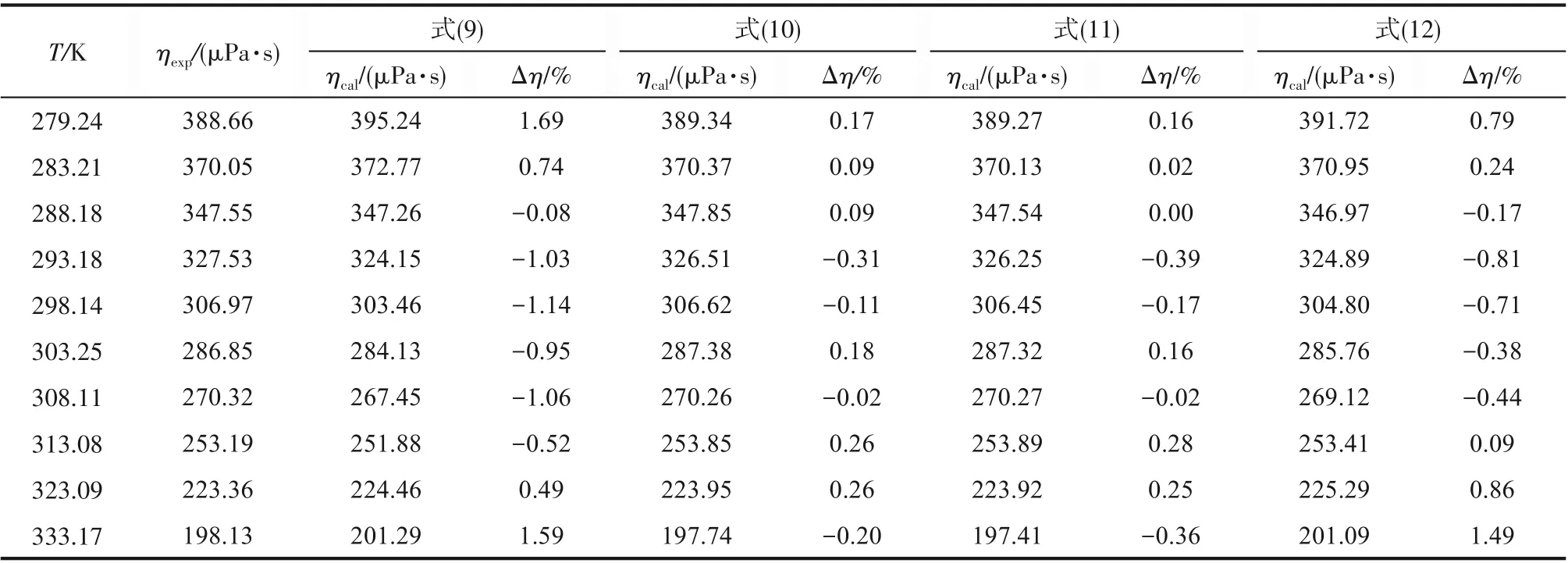
表7 四种模型的拟合结果与实验数据对比Table 7 The experimental data and correlation results of four viscosity models
本实验中采用四种模型对制冷剂R1336mzz(E)的黏度实验数据进行关联,从图4可以看出,选用修正后的非线性Andrade模型式(10)的方程得到最高的精度。同时,表6中C2的值与零相近,即非线性修正项的作用较小,R1336mzz(E)接近非极性流体,其动力黏度的自然对数lnη与温度的倒数1/T之间具有强线性关系,在精度要求不高的情况下可使用原始的Andrade方程进行实验数据的关联。
如前文所述,R1336mzz(E)有望成为高温热泵和有机朗肯循环中的替代制冷剂。根据热泵系统的分类,高温热泵的冷凝温度高于100℃[28],因此,R1336mzz(E)在高温下的黏度数据是其应用于有机朗肯循环及高温热泵研究中必不可少的一部分。根据四种模型的关联式,将R1336mzz(E)的黏度关系式外推到其临界温度(403.37 K),结果如表8与图5所示,由图5外推方程计算的液相黏度随温度的变化关系可以看出,本文外推方程的变化趋势合理。由图4关联方程的偏差分布可得,式(10)与式(11)的偏差数值较小且分布均匀,具有一定的可外推性,而式(9)与式(12)的外推性相对较差,在图5中表现为式(10)与式(11)的拟合偏差较小,两者在临界温度附近的外推结果也较为接近,即在临界温度附近黏度关系式(10)与式(11)的外推性较好,临界点处(403.37 K)式(11)相对于式(10)的偏差为-6.44%。由前文四种模型的拟合结果与偏差分析可得,式(10)在实验温度范围内的拟合误差小于式(11),在此基础上,可选用修正后的非线性Andrade模型式(10)的外推结果作为R1336mzz(E)临界点附近的液相黏度数据。
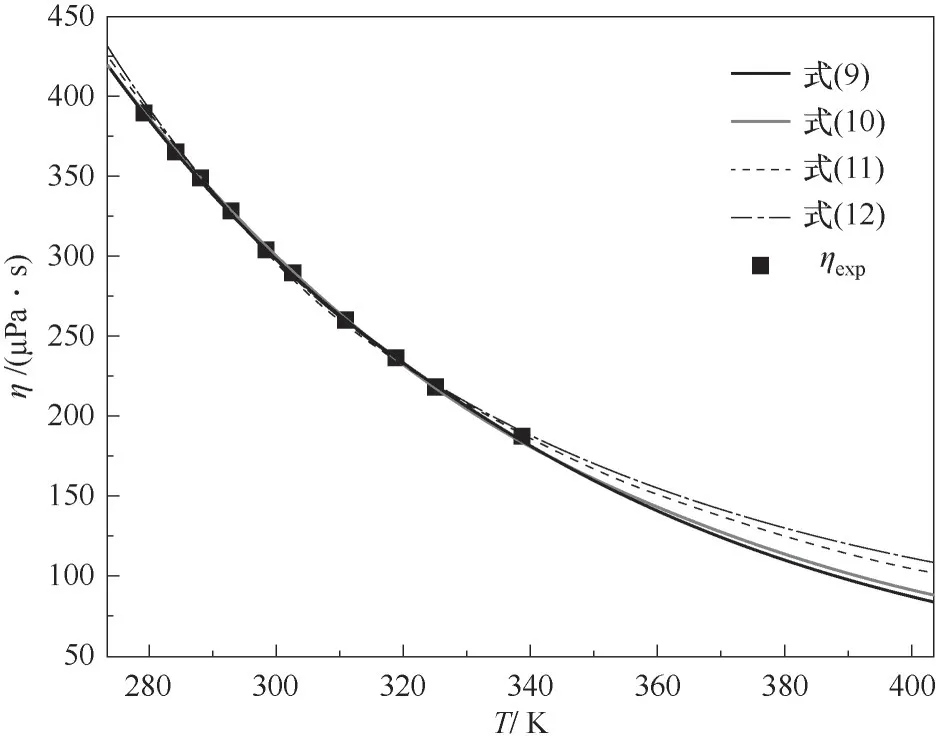
图5 R1336mzz(E)黏度的四种模型关联方程外推结果Fig.5 The extrapolation results of the four models of R1336mzz(E)viscosity
3 结 论
(1)使用旋转式毛细管黏度计,并将翻转升液法与承压容器相结合,在使用R22对实验装置完成标定后,进行新型HFO制冷剂R1336mzz(E)的液相黏度测量,温度范围为278~333 K。
(2)实验所得的液相黏度数据可以为R1336mzz(E)的应用研究提供基础数据,有助于新型制冷剂的替代工作。
(3)为了使实验结果能在工程中应用,采用四种形式的液体黏度方程对实验数据进行拟合,得到黏度依赖于温度的关联式,并将其外推到R1336mzz(E)的临界温度(403.37 K)。
(4)在四种模型中,修正后的非线性Andrade关联式精度最高,其拟合外推至临界温度的结果也最为可靠。
符号说明
M——摩尔质量,g/mol
p——压力,kPa
pC——临界压力,kPa
pS——饱和压力,kPa
R——气体常数,R=8.314 J/(mol·K)
T——温度,K
TC——临界温度,K
t——流出时间,s
u——不确定度
V——摩尔体积,m3/mol
η——动力黏度,μPa·s
ν——运动黏度,mm2/s
ρC——临界密度,kg/m3
ρL——饱和液相密度,kg/m3
ρV——饱和气相密度,kg/m3
ω——偏心因子
下角标
C——临界状态
L——液相
S——饱和状态
V——气相
