基于LMD-PE与神经网络的刀具故障诊断方法
2021-06-30杨瑞元何建樑王禹林
杨瑞元,尹 晨,何建樑,王禹林
(南京理工大学 机械工程学院,南京 210094)
0 引言
机械加工离不开机床的使用,在使用机床进行加工机械加工时,需要对对刀具的磨损状态进行精确地预测,以便在机械加工过程中提高机械加工的质量和效率。
在现有研究中,文献[1]采用BP神经网络融合多特征信息对刀具的状态进行监测,虽然提高了监测的效率,但是BP神经网络收敛速度慢,监测准度不高;文献[2]采用了长短期记忆神经网络对刀具的磨损状态进行监测,虽然提高了监测的准确度,但是采用小波包变化和滤波器来提取特征能量值,会丢失部分关键特征。
基于以上内容,本研究采用局域均值分解排列熵(LMD-PE)刀具状态的特征向量,输入到训练好的长短期记忆神经网络(LSTM)中进行预测,使刀具的故障诊断效率和准确性均得到大幅度的提高。
1 基于LMD-PE和LSTM的刀具故障诊断
刀具出现的故障形式通常有破损和磨损。破损大部分都是错误使用刀具造成的,磨损是正常使用中不可避免的[3]。产生故障的刀具在加工过程会产生不同的振动信号,因为产生的振动信号噪声大、信噪比低[4],采用LMD-PE对振动信号的处理和LSTM模型的训练对刀具的故障类型进行预测。下面对LMD、PE、LSTM的原理进行介绍。
1.1 局域均值分解LMD原理
LMD可以根据刀具振动信号的局部极值点,采用波动不大的迭代循环方法进行迭代循环,便能够将纯调频信号和包络小信号从原始的振动信号中分离出来[5],然后对纯调频信号和包络信号进行乘积得到PF分量,对于一个振动信号x(t),进行LMD分解的过程如下[6]:
1)x(t)是一个时间序列的振动信号,根据LMD原理首先要找出x(t)的所有局部极值点ni,计算极大值和极小值的均值以及包络估计值:
(1)
(2)
式(1)中,mi为两个极值的均值,式(2)中,ai为两个极值的包络估计值。
计算完成后,用直线将所有的mi,ai连接,然后采用移动平均法对连接后完成后的折线进行平滑处理[7],得到局域均值函数和包络估计函数。
2)分离局域均值函数:
h11(t)=x(t)-m11(t)
(3)
式(3)中,x(t)为原始振动信号的时间序列,m11(t)为局域均值函数,h11(t)为分离后得到的函数。
3)对分离后的h11(t)进行降调:
(4)
式(4)中,h11(t)为原始振动信号的时间序列分离局域均值函数后得到的函数,a11(t)为包络估计函数,s11(t)为h11(t)降调后的函数。
4)判断s11(t)是否为纯调频信号,当a12(t)=1时,则认为s11(t)是一个纯调频信号,如果s11(t)不是一个纯调频信号,则计算进行步骤1)~3),直至a1n(t)=1为止,需要强调的是,在实际的运算中,a1n(t)≈1即可停止迭代[8]。
5)计算第一个分量的包络信号:
(5)
式(5)中,a1n(t)为上述迭代运算产生的包络估计函数,p为迭代次数。
6)计算原始振动信号的第一个PF分量[9]:
PF1(t)=a1(t)s1n(t)
(6)
式(6)中,a1(t)为第一个分量的包络信号,s1n(t)为得到的纯调频信号。
7)将得到的第一个PF分量与原始振动信号的时间序列分离,得到一个新的时间序列,将得到的新的时间序列作为原始时间序列重复上述步骤1)~6),直到得到的新时间序列为一个单调函数为止,这时,原始振动信号的时间序列可以看做n个PF分量与最后的单调函数之和[10]:
(7)
式(7)中,uN(t)为最后得到的单调函数。
1.2 排列熵原理PE
排列熵是一种新的信息熵计算方式,能够度量一个时间序列的复杂程度,该方法不仅计算速度快,还能够准确地反映振动信号的微小突变行为[11],非常适合刀具的振动信号的处理和分析。其原理如下:
假设一个振动信号时间序列{X(i),i=1,2,…,N},采用相空间重构可以得到矩阵X[12]:
j=1,2,…k
(8)
式(8)中,τ为时间序列的延迟时间,d为嵌入维数,k为重构分量的数量,X(j)为矩阵X的第j行分量。
将X(j)按从小到大的顺序排序,确定每个元素在向量中的位置j1,j2,…,jd。因为重构矩阵的空间维数为d,所以一共会有d!种排列可能,此时排列熵[13]的计算公式为:
(9)
式(9)中,HP为排列熵,Pj为排列的概率。
进行归一化处理[14]:
(10)
最终得到的HP就是时间序列X(i)的排列熵。
1.3 长短期记忆神经网络LSTM
在LSTM模型中,该模型的算法特点能够对时间序列数据进行适当地预测,应用过程中采用了RNN循环神经网络模型,进行有效地改进,实现数据信息的计算。首先需要构建RNN循环神经网络,该模型在架构上包括输入层、隐含层和输出层[15]。其中隐含层在整个数据模型中具有举足轻重的作用,是算法的核心部分,该算法的架构如图1所示。

图1 RNN结构
图1中,x(t)为输入序列,h(t)为隐藏层序列,y(t)为输出序列。U、W、V为权重矩阵,则有:
ht=fa(Uxt+Wht-1+bh)
(11)
yt=fy(Vht+by)
(12)
式(11)、(12)中,fa、fy为激励函数;bh为隐含层的偏置向量;by为输出层的偏置向量。
RNN结构的隐含层如图2所示。

图2 RNN隐含层结构
采用RNN循环神经网络的目的在于:该模型具有较强的记忆功能,在处理关于时间序列数方面有突出的技术优势,但是容易出现梯度消失、梯度紊乱、记忆时间短等技术弊端[16]。
在本研究算法的计算过程中,采用改进型LSTM循环神经网络的特点在于:对RNN的隐含层的计算功能进行进一步地提升,下面通过模型结构对本研究的创新点进行说明,结构如图3所示。

图3 LSTM隐含层结构
在新型的架构设计中,在LSTM隐含层中融合多种智能控制门的计算,比如输入门、遗忘门和输出门等[17],即图中的ft、it、ot,输入门的作用是控制信息的输入,遗忘门的作用是对输入的数据进行预处理,输出门的作用则是控制信息的输出。图中,t-1时刻的细胞输出信息ct-1,ht-1经过函数φ1、φ2处理能够得到t时刻的细胞输出信息ct,ht,其中,φ1为sigmoid函数,φ2为tanh 函数[18]。
但是LSTM模型没有解决RNN模型的预测滞后问题,因此需要对LSTM模型进行改造,卷积神经网络(CNN)的优势在于能够从输入的信息中提取到更高阶的信息,同时把无用信息剔除[19]。基于此,本研究提出用CNN对输入的时间序列信息进行降维处理,提现更高阶的特征,再输入到LSTM模型中进行训练[20],这样训练速度就会大大加快,从而解决了预测滞后问题,同时CNN和LSTM使用相同的初始权重,不仅能够增强网络记忆模块的性能,还能减轻网络负载[21],具体结构如图4所示。

图4 改进LSTM模型结构
卷积神经网络和LSTM模型使用相同的全连接层,这样能够保证卷积神经网络提取的高阶特征能够完全传递到LSTM模型[22]。
1.4 刀具故障诊断
因为刀具在加工时的振动信号时间序列波动大,不宜直接输入到LSTM模型进行故障诊断,因此要先对刀具振动信号的时间序列进行LMD-PE运算,然后再输入到LSTM模型中,诊断的效果更好。
故障诊断的主要步骤:
1)采集刀具加工时的振动信号时间序列。
2)将振动信号发生的时间序列进行预处理,以获取较为纯净的数据信息,通过LMD算法模型,将振动信号分解输出多个PF分量,其中在这些PF分量中,能够提取刀具的故障类型[23]。
3)选取合适的PF分量,剔除与原始刀具振动信号相关系数低的PF分量[24],因为刀具在加工时的振动信号会有噪声干扰,这些噪声的振动会影响到故障的诊断结果。
4)将提取出来的PF分量进行空间重构,进而计算出排列熵。
5)选取排列熵特征向量。
6)最后将输出的刀具特征向量输入到训练的LSTM模型中,对提取的数据信息量进行训练。
7)得到诊断结果。
2 实验仿真
为了验证上述刀具故障诊断方法的有效性,通过在CNN数控车床上使用YT-15和YT16两种型号的硬质合金铣刀进行零件加工,这两种型号的主轴以1 200 r/min的转速进行旋转,刀具进给量以0.02 mm的位移进行,切削深度以1 mm的深度进行。然后通过振动传感器对刀具加工过程中的振动信号进行信息采集,采集频率为50 kHz,采集时间为1 s,对上述两种刀具的开始加工到报废全加工过程进行振动采集,每切削十分钟采集1次,将采集结果输入到电脑进行处理和分析,其中电脑的硬件配置CPU为inter i7-4500 h,运行内存为16 G,硬盘内存1 T。
在刀具工作过程中采集到的刀具信号进行LMD-PE运算,得到7个乘积分量和1个最终的单调函数,刀具的故障特征就包含在这些乘积分量中,但是采集的振动信号会受到噪音的影响,如果直接进行特征提取则最后的故障诊断结果不准确,所以要求取乘积值与原始序列的相关值,求取结果如表1所示。
在表1的数据信息中,可以发现以下数据现象:与原始时间序列的相关系数相比,PF1、PF2、PF5和PF7差距较大,这表明通过LMD模型之后,输出分解的的PF分量,相比于原始时间序列,存在较大的数据相关性,在这种数据信息中,将特征分量提取出来,其他数据信息分量与开始获取的时间序列的相关性就显得比较小,在进行数据分析时,就不将这些信息作为提取的重点来计算。为了提高数据分析的精度,需要将PF3、PF4、PF6和U这几个分量剔除处理。

表1 乘积值与原始序列的相关系数
刀具故障产生的根本原因是刀具在高速运转时与工件产生的摩擦力,即刀具在切削工件时,会受到工件的力[25],排列熵的计算就是捕获刀具与工件之间的相互作用力的变化,选择不同的嵌入维数就可以得到信号在不同频率下的故障特征,这就需要对信息数据中的多个维数中的排列熵进行计算,嵌入维数越多,排列熵值也会随之增加。不同维数之间的排列熵值区别很大,选取不同维数下的排列熵值没有交叉耦合的故障特征向量作为输入到模型中的向量。
为了验证本研究的技术效果,将相同刀具故障信息的特征向量分别输入到BP神经网络和本文的改进LSTM神经网络,观察二者之间的处理效果,然后进行故障分析、对比。在采用BP神经网络和LSTM神经网络这两种不同的算法模型进行刀具的磨损程度诊断时,一般会经历以下阶段,比如在进行刀具的磨损诊断时,存在初步磨损阶段、正常磨损阶段和剧烈磨损阶段,每个阶段分为前、中、后期,诊断结果如表2所示。
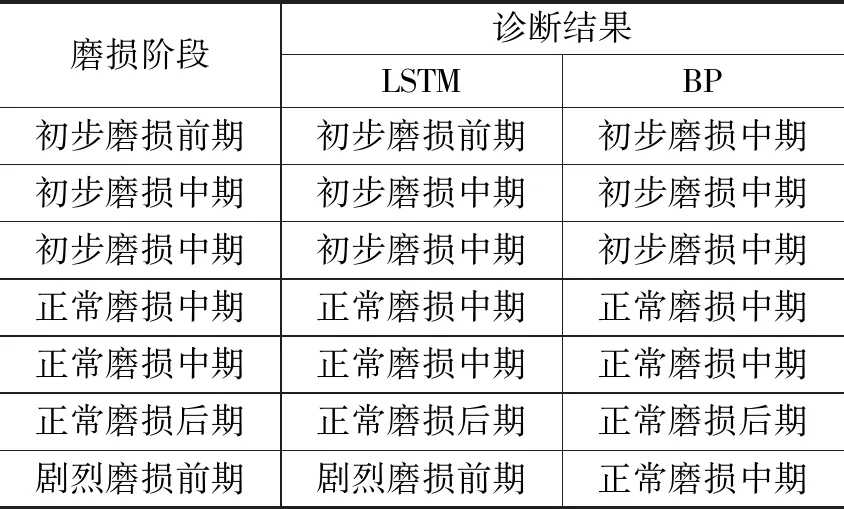
表2 刀具磨损程度诊断结果
通过表2中的数据可知,对于刀具磨损的诊断,LSTM的正确率比BP的正确率高。但是只根据对磨损的诊断结果并不能够判断方法对故障诊断的正确性,将两种神经网络的正确率进行统计,得到的正确率对比如图5所示。
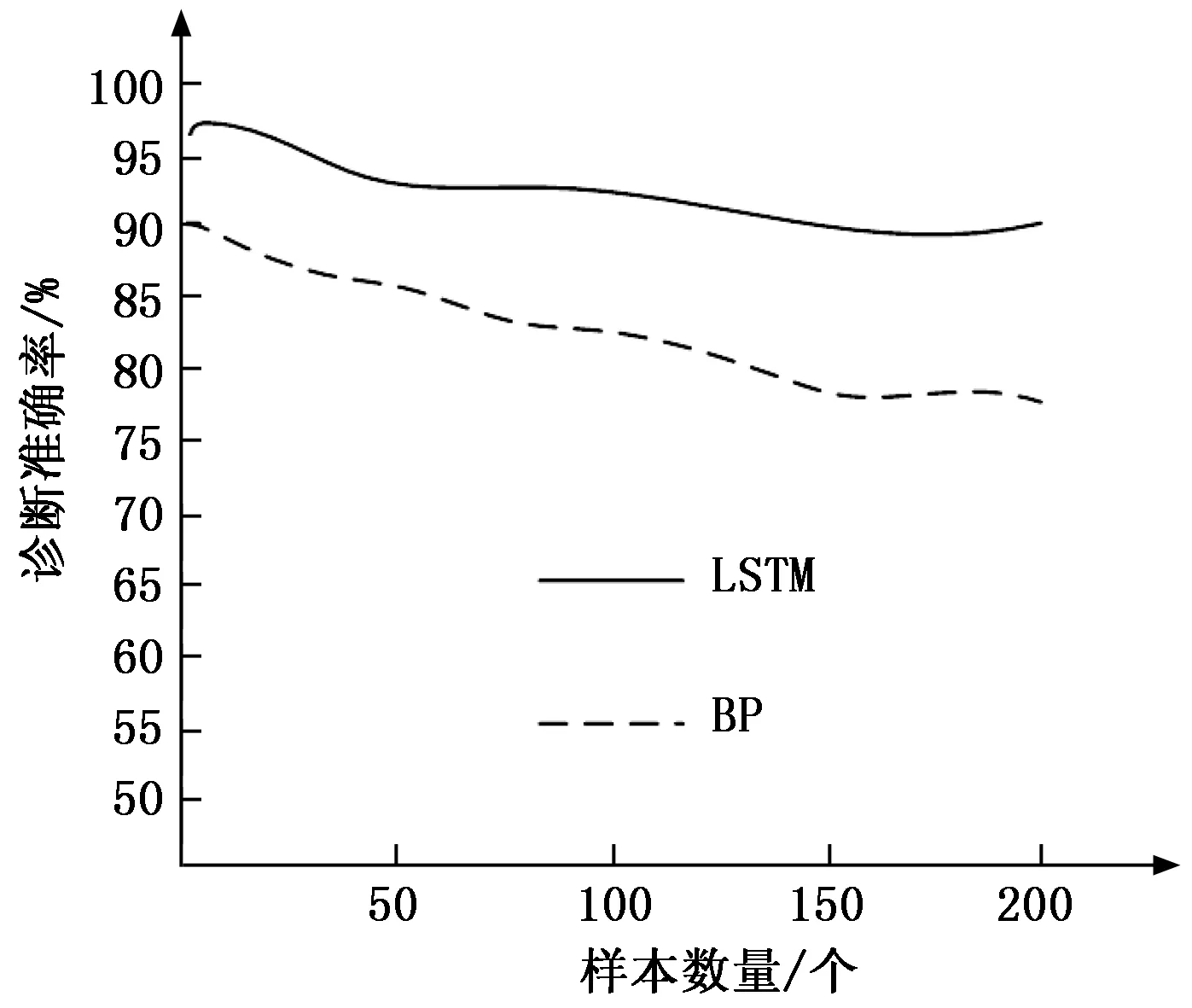
图5 两种神经网络的诊断正确率对比
通过图5可知,当试验的样本数量比较小时,利用LSTM模型的诊断时,其正确率在95%以上,BP模型的诊断正确率只有90%,随着样本数量的增多,两种模型的诊断正确率都随之降低,在样本数大于200以后,LSTM模型的诊断准确率稳定在92%左右,BP模型稳定在78%左右,提高了12%左右。
下面对上述改进的LSTM模型和传统LSTM模型的诊断效率进行对比试验,采用上述数据输入到两种模型中进行诊断,不记录诊断结果,只记录诊断所需时间,将结果进行整理得到数据,如表3所示。

表3 诊断时间数据
从表中数据可以看出,在相同的样本数量下,改进后的LSTM诊断时间比传统的LSTM诊断时间少,通过计算改进LSTM的诊断时间比传统LSTM诊断时间缩短了50%左右。
综上所述,上述提到的刀具故障诊断方法的可靠性高。
3 结束语
通过对刀具的振动信号进行LMD-PE处理,选取合适的特征向量输入到LSTM神经网络中对刀具的进行故障诊断,通过验证证明了方案的可行性并得出以下结论:
1)刀具的振动信号会受到噪声的影响,采集的信号不能直接提取特征向量。
2)排列熵的计算嵌入维数尽量选取大的,有利于特征向量的提取。
3)LSTM神经网络的诊断效率较慢,结合卷积神经网络可以提高效率。
上述的方案能够为刀具的故障诊断提供一定的思路,但是由于试验样本较少,故障诊断方法会有很多的不足,需要在实际的诊断中不断地改进和完善。
