两种不同类型土坡的失效风险定量计算方法探讨

2021-06-29吴超瑜陈文霞

广东水利水电 2021年6期

吴超瑜，陈文霞，潘健

(1.广东源天工程有限公司，广东广州 511340；2.华南理工大学土木与交通学院，广东广州 510640)

1 概述

土坡工程的稳定性分析受到诸多不确定性因素的影响，而极限平衡分析法中用安全系数的方式来表达不明确的、难以预知的因素，并将这些不明确的、难以预知的因素试图进行定量化，从而将不确定性因素用容易表达的安全系数来表示，具有一定的确定性。然而，土坡稳定性直接影响着工程的安全性，土坡一旦发生失稳，则可能导致财产损失和人员伤亡，带来极大的工程风险[1]。因此，在土坡风险分析中考虑不确定性因素是十分重要的[2-3]。将可靠度理论引入土坡评价体系中，建立安全系数与失效概率的关系，将两种评价体系结合起来是近年来土坡稳定性研究的一个重点和难点[4]。

随着计算机软件与技术的进步，土坡的可靠度分析和失效概率计算精度的提高有了十分有效的途径和方法。近些年来，不少国内学者也做了关于此方面的研究工作。李典庆[5]在子集模拟的基础上，提出了一种高效随机有限元法(RFEM)进行土坡的可靠度分析以及风险评估，并且推导了计算公式。邓志平等[6]采用蒙特卡洛法进行模拟，在考虑地层变异性和土体参数固有变异的情况下提出了一种边坡可靠度的模拟分析方法。

本文根据整个项目从勘察到项目结束所掌握的场地条件、勘察情况、设计、施工、监测等信息情况，将土坡工程进行分类，在此基础上尝试建立安全系数与失效概率间的关系。

2 分析方法

可靠性理论是研究系统运行可靠性的普遍数量规律以及对其进行分析、评价、设计和控制的理论和方法，它以概率论和数理统计为主要研究工具，在土坡稳定性分析中有较为广泛的应用。土坡可靠度常用可靠度指标或失效概率衡量土坡的稳定性程度。土坡可靠性分析的基本原理为：在对土坡工程系统进行地质分析的基础上，确定土坡的破坏模式，将岩土体性质状态参数、土坡机会参数、荷载、地下水压等随机变量用合理的分布函数描述，并选择合理的破坏准则，建立土坡破坏的数学模型，选择合适的可靠度计算方法，进行土坡的稳定性评价，确定土坡在使用年限内发生破坏的概率。

假设状态函数Z=G(X)=R-Q，R为抗滑力的状态函数，Q为滑动力的状态函数。若Z≥0则土坡处于可靠状态，若Z<0则土坡处于破坏状态，X=(x1,x2…,xn)为随机变量，代表土坡内随机点处于稳定状态下其所受到的各种控制的因素，具有一定的分布，常见主要有正态分布、对数正态分布和Beta分布[7-8]。x1,x2…,xn，为影响土坡稳定的变量，如土体重度γ、粘聚力c、摩擦角φ、孔隙水压力u，计算模型、地下水等。

假定随机变量呈正态分布，则破坏概率Pf可表示为[8]：

(1)

其中β为可靠度指标，在土坡稳定性分析中最常用的表达形式为：

(2)

式中μR、μQ、σR、σQ分别为状态函数R、Q的均值和方差，ρRQ为状态函数R、Q的相关性。其中:

(4)

其中xi为某一参数样本统计值，n为样本数。

由上述公式，可求出土坡失效概率和可靠度指标，且β越大，Pf越小，土坡安全程度越高。

3 土坡失效概率计算

3.1 土坡分类

在分析、设计、施工和维修过程中，安全系数的应用是具有现实意义的。即在“事前、事中、事后”3阶段中，(设计)事前需详尽地检测相关土体材料的性状；(施工)事中动态地进行监控，即包括施工全流程中对土体的连续动态监测，也包括过程中根据实际情况及监测数据，对原设计思路进行细节上的完善、调整；只有这样，在(完工投入使用)事后，整个设计体才更符合客观规律、更满足安全需求。

本文根据土坡工程的特征、性状以及“3阶段”期间分别采取不同策略的前提时，列举两种不同情况下的土坡。

情况1：土坡工程在事后阶段发生了造成严重影响的破坏(包括财产和生命损失)。事前(勘察、设计阶段)对施工区域及周边环境均进行了详尽的地质试验、分析及现状性状分析，并通过计算得到土坡稳定安全系数Fs，考虑应力路径对土坡稳定性的影响，观测孔隙水压力和其它相关参数的变化情况；事中(施工阶段)通过每天的土体监测，将理论与实际相比较，判断理论计算、分析的可靠性。

情况2：土坡破坏的后果较为严重。事前(仅勘察阶段)对周边环境进行了分析并进行了有选择性的试验，通过性状试验再综合现场情况进行判别，采用有效应力确定土坡稳定安全系数Fs；施工阶段，由专门人员定期进行监测和检查。

3.2 土坡失效概率

美国著名学者Baecher[9]和Whitman[10]根据大量土坡工程经验得到如下判断：当土坡稳定安全系数取值1.5时，第2种情况中的土坡其发生破坏的概率为0.000 1；而同为麻省理工学院的Lambe教授[11-12]则认为第1种情况下，当Fs=1.3时，土坡的失效概率为Pf=0.000 1。

假定安全系数服从正态分布，变异系数V为常数，不考虑状态参数间的相关性，则：

β=-φ(Pf)

(5)

(6)

根据公式(5)(6)，可以绘制出在两种情况下土坡稳定安全系数与失效概率之间的关系(如图1所示)。

图1 安全系数与失效概率的关系示意

由图1可知，对于两种不同的情况下的土坡，当Fs<1.2时，安全系数的提高，土坡失效概率降低不明显；当Fs>1.2时，随着安全系数的增加，失效概率之间的差值急剧增大。因此在实际工程中将设计、施工与监测三者结合起来，建立动态反馈机制，不断加深对土坡相关信息的了解，并对工程出现的问题及时采取有效措施，才能有效降低土坡的失效概率。

3.3 土坡失效风险分析

考虑到土坡设计、施工成本以及隐含的预测破坏后果，可以使用可靠度指标进行成本—效益之间的经济关系分析。优化设计是从多种方案中选择最佳方案的设计方法。它以数学中的最优化理论为基础，以计算机为手段，根据设计所追求的性能目标，建立目标函数，在满足给定的各种约束条件下，寻求最优的设计方案。这个过程中，可靠度指标就是设计追求的性能目标，而设计、施工成本以及隐含的预测破坏就是给定的各种约束条件，这样的分析过程能减少主观判断的影响。

风险分析所提供的逻辑程序能帮助工程人员理解施工风险的不确定性，并从认识、了解、评价及如何采取减灾灭灾措施等方面，使工程人员对灾害的把握方面有着更为实用的分析工具，其流程如图2所示。风险评价可以从详细到准确。在工程中，设计工程师一般根据数据做决定，而定量化的风险分析方法在设计和施工中能产生重要影响。

图2 风险分析的流程示意

土坡的风险分析包括两个方面：一是方案决策风险；二是土坡失效的风险。

决策风险，是指在决策活动中，由于主、客体等多种不确定因素的存在，决策活动不能达到预期目的的可能性及其后果。对于土坡工程来说，其方案决策风险为可能因土坡破坏而造成严重后果。这里面的风险又包括有发生的可能性，以及发生后的严重性。前者主要指土坡的失效概率，后者对社会、经济及人身安全造成的损失可用下式进行计算：

C=Pc(Cc+PfCf)

(7)

式中C表示土坡的总风险损失；Pc，Pf分别为选择某一设计方案的概率和土坡失效概率；Cc为该设计方案的费用，主要指有关土坡的施工成本；Cf为土坡失效造成的损失。

4 工程实例

4.1 工程概况

广东省某土坡工程项目平面布置如图3所示，场地的工程地质条件如下：岩土分布主要是泥盆系强风化、中风化、微风化砂岩，岩体节理裂隙发育，结构面倾向与土坡倾向存在不利组合。地下水主要为基岩裂隙水，其中强风化及中风化细粒砂岩为主要含水层，受大气降雨补给，含水量小，排泄条件较好。场地区内无地表水体，坡体上溪流不发育。

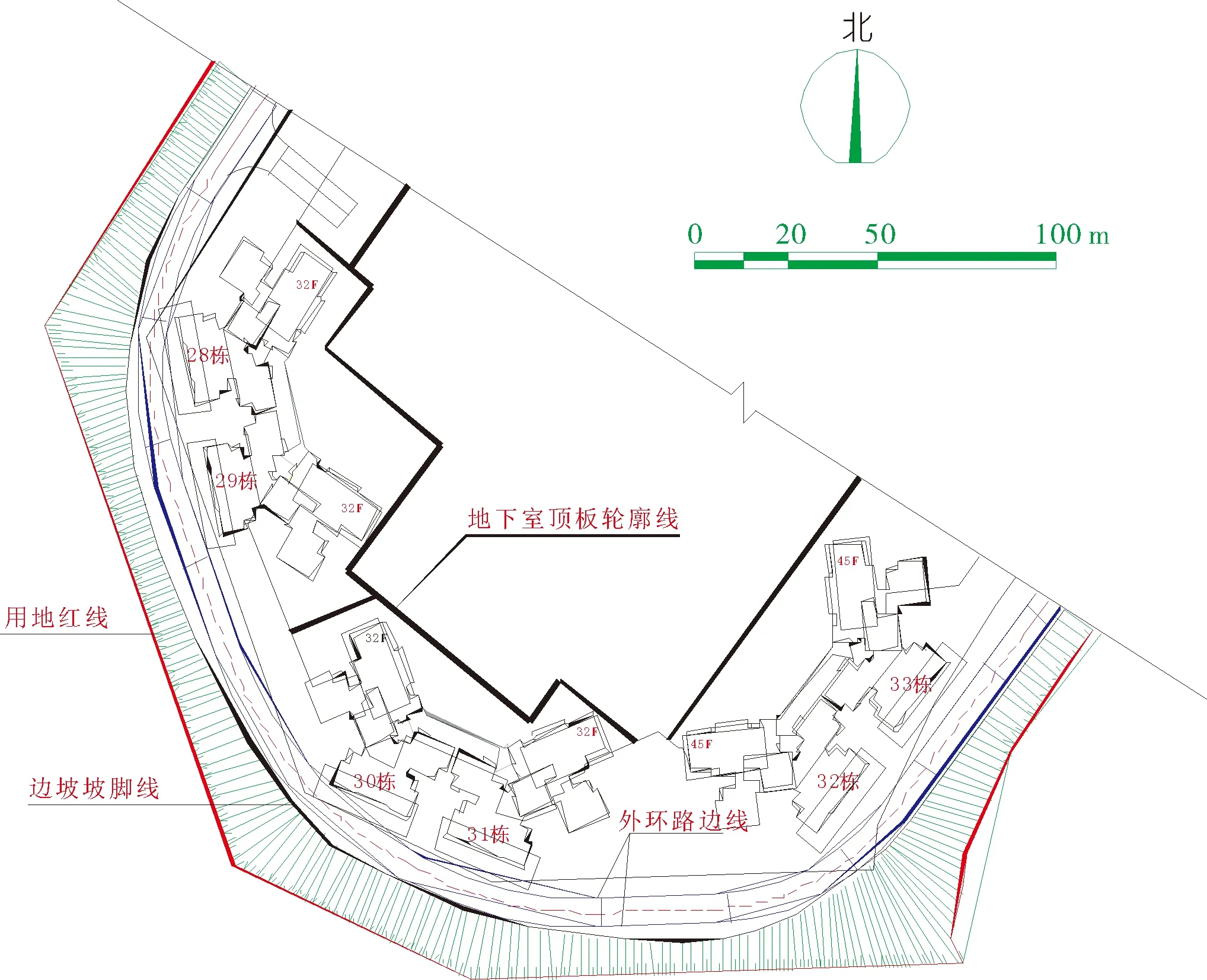
图3 场地平面示意

场地建筑物基础工程开挖后，3面环山处分别形成了3处高度为8～48 m，坡度在35°～70°之间的土坡。为了保证建筑物周边场地的永久稳定，建设方同意采用“分台阶放坡+分层分段治理+地表排水+格构梁+钢筋锚杆+绿化”的土坡综合治理方案。

各层土体主要物理性能指标见表1所示。

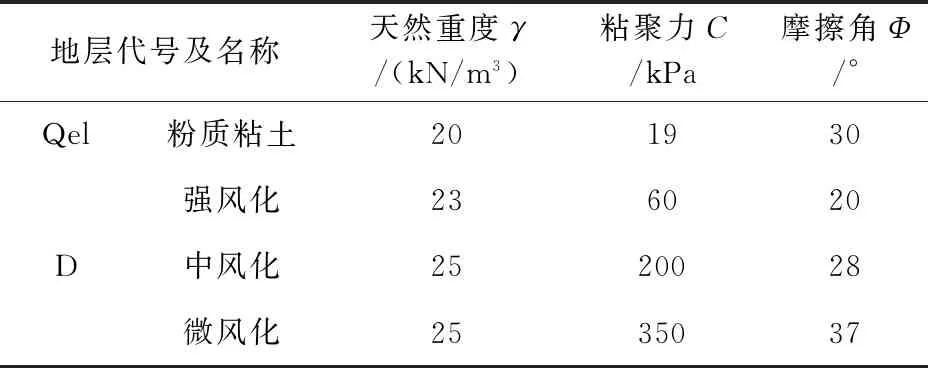
表1 各土层主要物理性能指标

4.2 土坡失效风险分析

该土坡安全等级为一级，详细勘察单位需要提供土坡场地位置、地质条件、场地复杂程度，分析场地周围环境，同时采用场地原位试验和实验室试验相结合的方式测量土体强度参数；在施工过程中进行土坡变形监测，完工后仍对土坡继续进行为期2 a的监测。因此该土坡为前述情况1所示的土坡，可以通过对本工程土坡场地最不利处的40 m长土坡剖面进行稳定性分析。图4为最不利处土坡的剖面示意，图5为相应的土坡三维模型网格划分示意。

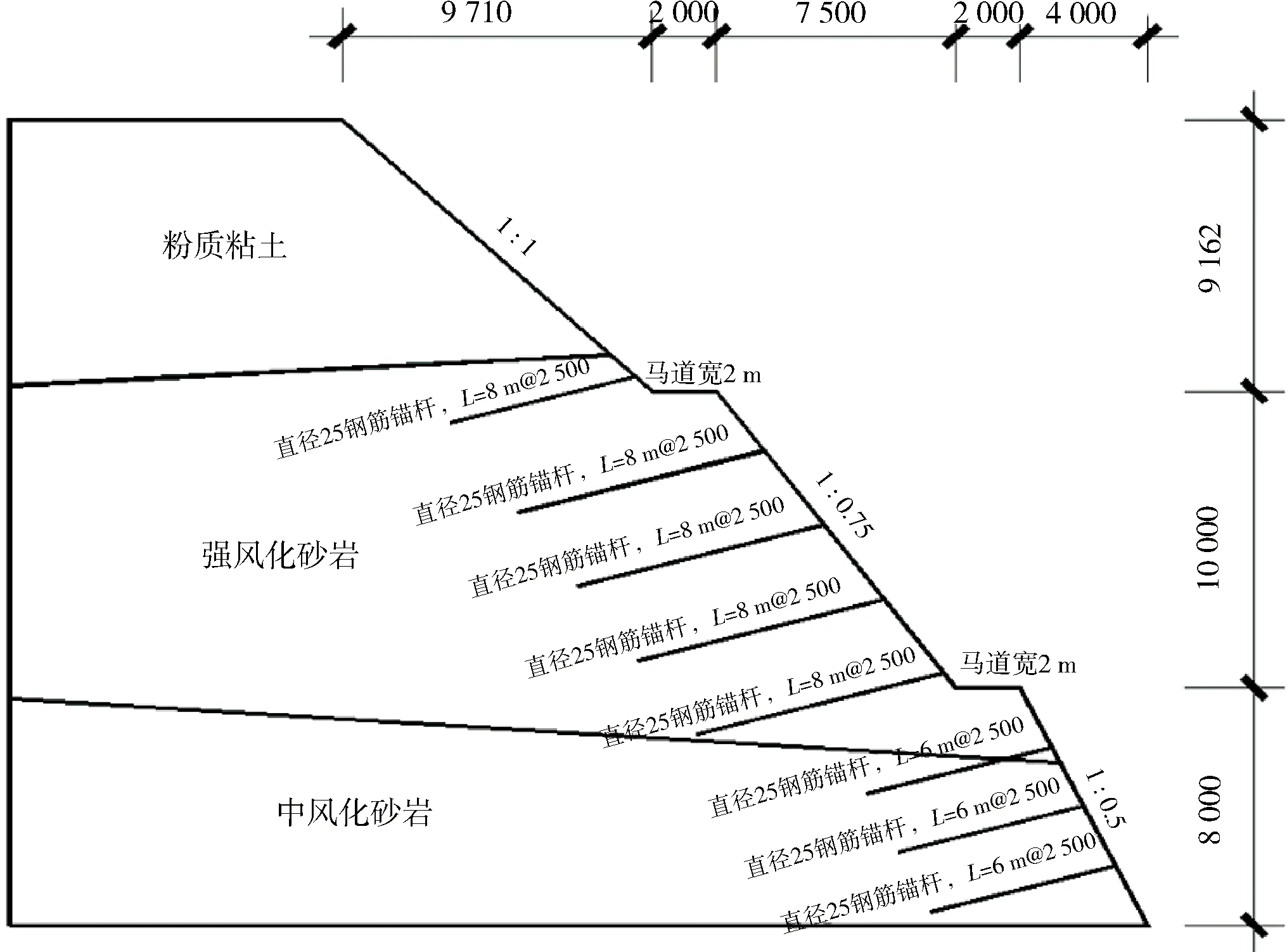
图4 典型剖面几何尺寸示意

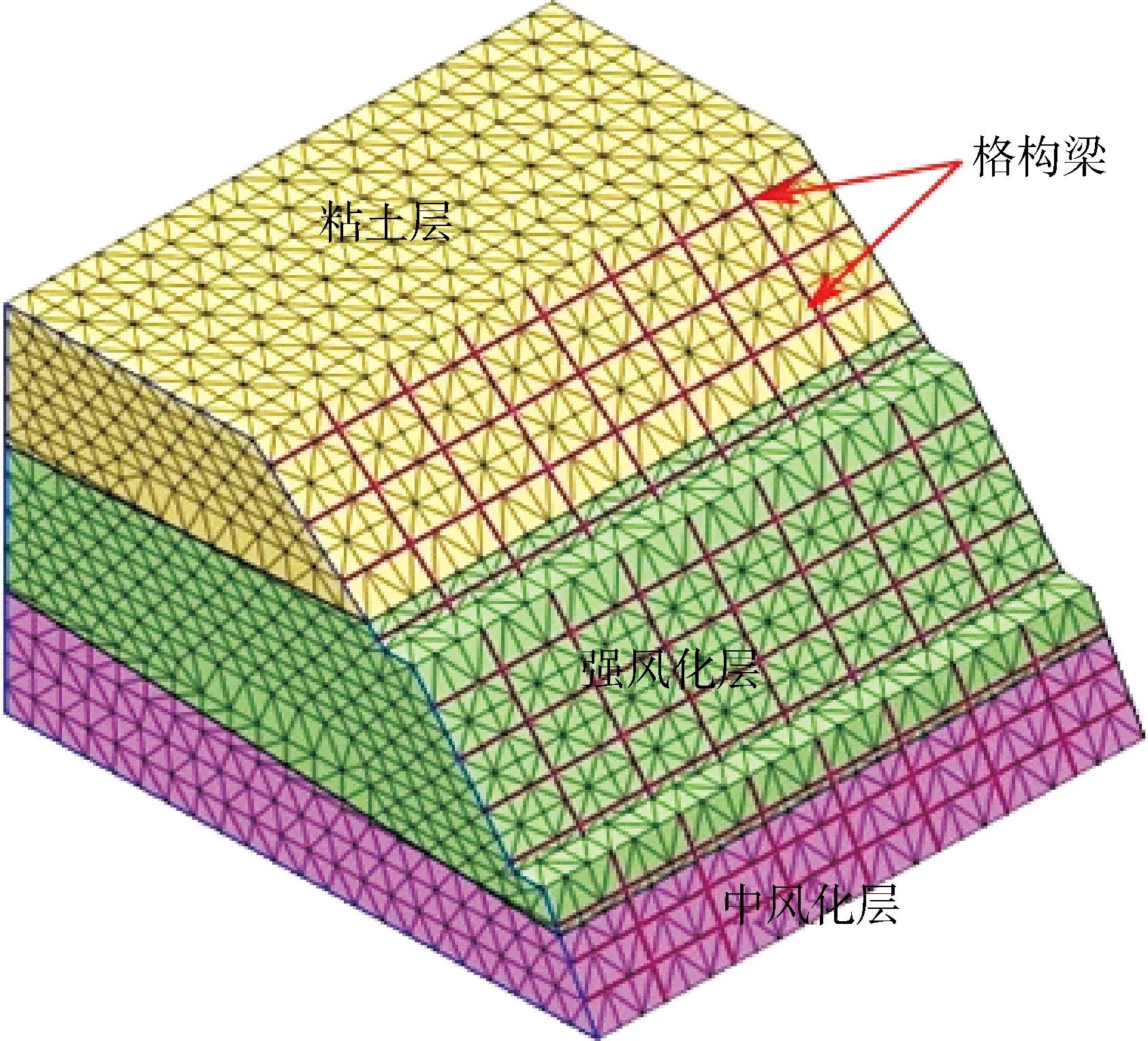
图5 三维土坡模型网格划分示意

土坡处理有两种方案。方案1为削坡之后，不采取加固措施时，有限元分析计算的土坡安全系数为1.14，由图1安全系数与失效概率的关系可知，与此对应的土坡失效概率为0.016；方案2增加了支护结构，有限元分析计算的安全系数为1.65，与之对应的失效概率为1×10-10。由此对整个土坡的稳定性进行风险评估：若第1种情况下发生土坡破坏，估算滑坡量约为14 500 m3，相关财产损失约为90多万元，且可能造成人员伤亡；若第2种情况下土坡发生滑坡，相关财产损失大约为240万元，滑坡量为1 800 m3，造成的财产损失大约为25万元，无人员伤亡。

假定两种方案采用的概率均为0.5，滑坡后岩土体处理单价按300元/ m3计算，则第1种情况下的风险损失约为1.7万元；第2种情况下的风险损失为120万元。虽然方案2的风险损失较大，但考虑到土坡破坏后的社会影响程度，仍选择方案2。