采用JADE-SVR方法研究波浪和开孔沉箱相互作用

赵沛泓，孙大鹏，吴 浩

(大连理工大学 海岸和近海工程国家重点实验室，大连 116024)

开孔沉箱结构能够显著降低波浪能量，改善工程海域的波况并减轻结构自重，在保证结构安全可靠的前提下产生良好的经济效益，目前，在海域海岸工程中已有广泛的设计应用。

1 研究背景

自20世纪60年代Jarlan[1]等提出开孔沉箱概念以来，国内外学者对开孔沉箱的消浪特性做了很多物模试验研究[2-6]。然而以往试验数据通常采用传统的多元线性回归方法，分析给出特征物理量和诸多影响因素的计算关系式。这种方法首先要进行单变量分析，将非线性问题线性化，逐一确定每个单变量对特征物理量影响的函数关系(以幂函数为主)，进而利用最小二乘法给出最终的拟合公式。拟合公式的拟合精度与泛化性能有着天然的内在矛盾，用何种策略平衡这一矛盾，使两者都能达到令人满意的结果，是许多学者关注的重点。对于传统的多元回归分析方法，通过单变量分析+最小二乘估计的操作过程给出最后的回归函数表达式，由于最小二乘估计是一固定过程不存在分歧，回归函数的拟合精度和泛化性能，几乎全部由单变量分析决定，然而恰恰是这一过程完全由人工完成，存在着很强的随意性。

传统多元回归分析方法存在缺陷的根源是缺乏保证回归函数拟合精度与泛化性能同时满足条件的机制或说“策略”。而具有相应“策略”指导的机器学习方法无疑是另外一种可行的选择。

支持向量机SVM是Vapmik等人在1995年[7]基于统计学习理论提出的一种新型的机器学习方法，它用结构风险最小化策略代替传统的经验风险最小化策略，使之较传统的机器学习方法具有更好的泛化性能。支持向量回归机SVR是SVM在估计函数、处理回归问题上的推广。在港口工程领域，SVR的应用较少，2011年Patil S G[8]等利用遗传算法优化的SVR研究了浮水管式防波堤的透射系数与相关变量间的关系，结果表明，通过SVR学习得到的模型能够很好地描述各物理量的非线性关系。

本文利用带有外部存档的差分进化算法(JADE)优化的SVR对开孔沉箱波浪反射系数及所受波浪力与各影响因子的关系进行回归分析，对比传统多元回归分析方法，评价两种回归模型的拟合精度和泛化性能，探讨SVR在港口建筑物设计领域旳应用前景。研究结果表明：SVR方法对开孔沉箱波浪反射系数及波浪力的分析具有适用性，与物模试验值相比，其结果优于传统多元回归方法的分析结果。

2 试验概况

本文中物理模型试验在大连理工大学海岸和近海工程国家重点实验室的波浪水槽内进行，如图1所示，水槽长56 m、宽0.7 m、最大试验水深0.7 m。造波端安装有液压伺服推板式造波机，模型布置在距离造波机35 m处，水槽末端铺设消能缓坡装置。

图1 二维试验波浪水槽Fig.1 The flume used in the experiment

开孔沉箱模型采用1.0 cm厚的有机玻璃制成，模型设计为无顶板形式，前墙开孔、后墙实体，消浪室宽度bc分别为0.15 m、0.20 m、0.30 m。开孔形式为矩形开孔，开孔率μ采用20%、40%两种型式，开孔位置从水下0.2 m至顶部，等间距开4排孔，不开孔部分均用石子填充。基床前试验水深d保持0.4 m不变，基床前后肩宽W均为0.25 m。沉箱模型放置在不同高度的基床上，基床高度hm分别为0 m、0.10 m、0.15 m、0.20 m。图2为模型外观示意图。

图2 开孔沉箱模型示意图Fig.2 Perforated caisson used in the experiment

为了计算开孔沉箱前波浪反射系数，在沉箱前不等间距布置5个浪高仪，其位置如图3所示，对于不同的试验波要素选取适当的浪高仪组合进行数据分析，采用合田良实的两点法分离入、反射波，进而计算出反射系数。

为了计算开孔沉箱所受波浪力，如图4、图5所示，在沉箱开孔板迎浪面、背浪面、后实体板和底板的上面和下面布置多点压力传感器，点压力布置情况如图3所示。图中●表示前墙迎浪面和底板测量浮托力点压力布置情况；○表示前墙背浪面和底板测量渗流力点压力布置情况。通过采集各个点压力仪的同步时间序列，积分得到结构受到的总水平力和总垂直力。

图3 试验模型布置图Fig.3 Wave flume and the setup of the model experiment

试验过程中的波浪条件和模型尺寸变化由表1给出。

表1 试验条件及试验参数变化范围Tab.1 Experimental conditions and the scope of experimental parameters

3 试验结果及分析

3.1 确定开孔沉箱波浪反射系数及波浪力的影响因素

根据LI[9]的分析，开孔沉箱波浪反射系数Kr与相对基床高度hm/L1/3、相对消浪室宽度bc/L1/3、相对水深d/L1/3、波陡H1/3/L1/3及开孔率μ有关，最终反射系数Kr可表示为

(1)

而开孔沉箱所受波浪力可分为总水平力与总垂直力。总水平力为沉箱迎浪面、背浪面与消浪室后实体板所受波浪力合力；总垂直力为消浪室中动水压力与沉箱底部所受浮托力的合力。如图6所示，由于开孔沉箱的结构特性，其所受到的总垂直力与总水平力之间存在一定的相位差，即两者不在同一时刻到达峰值或谷值。用Pv表示沉箱所受总水平力达到极值时刻对应所受的总垂直力，Pv0表示沉箱在全时间段内所受的总垂直力极值，定义Pv/Pv0为水平力极值时刻对应的总垂直力相对于总垂直力极值的折减系数，可表示为

图6 不规则波作用下开孔沉箱受力的时间过程线Fig.6 Time series data of total wave forces acting on perforated caisson by irregular waves

(2)

3.2 JADE算法优化的SVR模型

假设有训练样本集{(xk,yk)|xk∈Rd,yk∈R,k=1,2…n}，在SVR算法中，目标是寻找一个函数f(x)=wTx+b，使其尽可能平坦且允许样本值的最大偏差为ε，其中w∈Rn，b∈R，对于容量为l的样本集，采用ε-不敏感损失函数度量经验风险，即有

(3)

(4)

式中：常数C体现了f(x)的平坦程度与允许样本最大偏离程度的折衷。上式是典型的二次规划问题，可以引入Lagrange函数

(5)

(6)

也等价于拉格朗日对偶问题形式

(7)

根据KKT条件，该极值可通过对拉格朗日函数求导得到

(8)

(9)

(10)

(11)

(12)

通过求解上述最大化问题，可得线性回归函数为

(13)

当样本为非线性时，可以先通过非线性映射将原空间中的输入量x映射到高维Hilbert空间，即x→φ(x)，其中φ(x)∈H，然后在H空间中构造最优超平面

(14)

然而对φ(x)进行显式表达是困难的，根据Mercer定理，可以找到一个对称半正定的有效核函数，直接表达出映射函数的内积形式，即

K(xi,x)=<φ(xi)·φ(x)>

(15)

非线性回归优化问题和线性回归优化问题形式相同，不同之处仅在于样本输入向量变成了向量的映射函数，可以发现映射函数及核函数的引入不影响优化过程，最后，SVR给出的非线性回归函数为

(16)

本文采用径向基函数(RBF)作为核函数，即

(17)

SVR的泛化性能与求解过程中几个参数的取值密切相关，这些参数分别是惩罚系数C、损失函数中的参数ε和核函数参数g，常采用启发式算法优化这些参数。常见的启发式算法包括遗传算法、粒子群算法、差分进化算法、模拟退火算法等。

本文采用Zhang[10]提出的带有外部存档的差分进化算法对C、ε、g三个参数进行寻优，寻优过程可以概括为以下几步：

(1) 随机生成20组参数初始值{(Ci,εi，gi)|i=1,2,…,20}，每一组参数初始值可以看做是种群中的一个个体，20则代表种群规模；

(2)将训练样本集分为5份，取第1份作为预测数据，其余4份作为训练数据；

(3)将参数值代入优化问题(12)，求解回归模型，利用模型对预测数据进行计算，得到均方误差值；

(4)再依次取训练样本集中的第2、3、4、5份作为预测数据，其余作为训练数据，重复上一过程，得到4个均方误差值；

(5)计算总共5个均方误差值的均值，作为一步进化过程的个体适应度值，20组参数得到20个适应度，其均值为种群平均适应度，最小值为种群最优适应度；

(6)利用差分进化算法原理进行变异，交叉，选择操作，得到下一步进化过程的种群，计算新的种群平均适应度，种群最优适应度；

澳大利亚不同年龄段消费者对于酒种的偏好具有较大差异：14～17岁年龄段消费者更偏爱喝预调烈酒，但随着年龄增长，喜爱瓶装葡萄酒的消费者占比逐渐增加，而预调烈酒的占比逐渐减少。对于烈酒，14～17岁年龄段消费者消费烈酒比例占该群体总消费酒精饮料的60%，为各年龄阶段群体中最高。但随着年龄的增加，消费者饮用烈酒的比例总体上呈下降趋势，18～24岁年龄段消费者消费烈酒的比例占该人群总消费酒精饮料的22%，为各年龄阶段群体中最高。25～29岁及30～39岁消费者消费普通烈度啤酒占该人群总消费酒精饮料的27%，为各年龄层最高。具体情况见图2。

(7)重复上一过程，则种群不断进化，最终达到最大进化步数。这时具有最优适应度的个体代表的参数值，可以认为是最优参数组合。

参数寻优过程中的(2)～(5)即为通常所说的K-折交叉验证，本文取K=5。

现有波浪和开孔沉箱相互作用的试验数据216种工况组合，其可分为两部分，一部分作为SVR模型的训练数据，一部分作为模型的测试数据，这里随机抽取162组数据作为训练数据，其余54组数据作为测试数据。事实上，前人基于传统多元回归分析方法拟合公式，是将全部试验数据进行拟合，而没有划分另外的数据进行验证，所以JADE-SVR中提到的“训练数据”和“测试数据”的概念对这些回归模型没有意义，但是为了便于比较，仍然给出传统模型对“训练数据”和“预测数据”的计算结果，这也相当于在一定程度上高估了传统多元回归分析模型的预测性能。

以反射系数试验中162组“训练数据”为例，进行JADE-SVR模型参数寻优，图7给出了寻优过程中最优适应度和平均适应度的收敛情况，图7横坐标表示差分进化算法的迭代次数，纵坐标表示适应度值，根据前述参数寻优过程可知，适应度即为SVR模型的均方误差平均值，其值越小，则SVR模型预测性能越好。由图可以看出，一方面，种群平均适应度下降平缓，表示进化过程中种群多样性没有突然性的降低，减少了算法发生“早熟”的可能性，另一方面，迭代后期，平均适应度收敛于最优适应度，表示种群中优良个体保存良好，避免了算法陷入类似随机搜索的可能。

图7 JADE算法适应度曲线Fig.7 Fitness curves of optimizing SVR parameters using JADE algorithms

3.3 JADE-SVR模型与传统多元回归模型的对比

根据求得的最优参数，建立JADE-SVR回归模型，对训练数据和预测数据进行计算，并与传统回归分析模型给出的计算值作比较。为了量化比较结果，引入四个评测指标，分别为偏移率Bias、均方根误差RMSE、散射指数SI和相关系数R，其定义如下

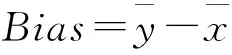
(18)

(19)

(20)

(21)

关于反射系数，分别采用SVR模型、行天强[11]推荐计算公式及2011年《防波堤设计与施工规范》[12]推荐计算公式，对训练数据和预测数据进行计算，所得结果与试验值对比，其中，SVR模型与行天强[11]推荐计算公式是由相同试验数据拟合得到的，2011年《防波堤设计与施工规范》推荐计算公式是由暗基床开孔沉箱试验数据拟合得到的。各统计评价指标如表2～3所示。由表可知，无论对训练数据和预测数据，JADE-SVR性能都显著超过传统多元回归模型。由图8所示，利用JADE-SVR模型所得计算值更加接近真实值，故而能很好地描述反射系数与各无因次变量间的函数关系；另外，JADE-SVR模型不仅对训练数据的计算达到很高精度，对预测数据也有良好的计算精度，没有出现机器学习过程中易发生的“欠拟合”和“过拟合”现象。

表2 三种模型关于波浪反射系数计算性能对比(训练数据)Tab.2 Comparison on computing the wave reflection using three different models (train data)

表3 三种模型关于波浪反射系数计算性能对比(预测数据)Tab.3 Comparison on computing the wave reflection using three different models (test data)

图8 反射系数计算值与试验值比较Fig.8 Comparison of Kr between measured and calculated results

表4 三种模型关于水平力峰值时刻垂直波浪力折减系数计算性能对比(训练数据)Tab.4 Comparison of computing the wave reflection using three different models (train data)

表5 三种模型关于水平力峰值时刻垂直波浪力折减系数计算性能对比(预测数据)Tab.5 Comparison of computing the wave reflection using three different models (test data)

图9 水平力峰值时刻垂直力折减系数Pv/Pv0计算值与试验值比较Fig.9 Comparison of Pv/Pv0between measured and calculated results

关于垂直波浪力折减系数Pv/Pv0，分别采用SVR模型、冯延奇[13]推荐计算公式及2011年《防波堤设计与施工规范》推荐计算公式，对训练数据和预测数据进行计算，所得结果与试验值对比，其中，SVR模型与冯延奇[13]推荐计算公式是由相同试验数据拟合得到的，2011年《防波堤设计与施工规范》推荐计算公式是由暗基床开孔沉箱试验数据拟合得到的。表4～5给出关于水平力峰值时刻对应垂直力折减系数计算评价结果，表6～7给出水平力谷值时刻对应垂直力折减系数计算评价结果。与反射系数计算结果类似，SVR模型给出的计算结果仍好于传统回归分析方法计算结果，而《防波堤设计与施工规范》推荐公式计算结果精度偏低，原因在于其没有考虑基床高度的影响，只适用于暗基床形式开孔沉箱的计算。

表6 三种模型关于水平力谷值时刻垂直波浪力折减系数计算性能对比(训练数据)Tab.6 Comparison of computing Pv/Pv0 using three different models (train data)

表7 三种模型关于水平力谷值时刻垂直波浪力折减系数计算性能对比(预测数据)Tab.7 Comparison of computing Pv/Pv0 using three different models (test data)

值得注意的是，在以往的工作中，无论是行天强[11]对反射系数Kr或是冯延奇[13]对垂直波浪力折减系数Pv/Pv0给出的多元回归分析模型，都是将全部216组试验数据进行拟合，而没有像本文一样，只取其中一部分作为拟合数据，另一部分单独划出作为预测数据，对拟合后的公式进行预测精度的验证。因此可以认为在本文中这些多元回归分析模型的预测精度在一定程度上被高估了。

图10 水平力谷值时刻垂直力折减系数Pv/Pv0计算值与试验值比较Fig.10 Comparison of Pv/Pv0between measured and calculated results

综合来看，JADE-SVR模型相比传统回归分析模型，回归预测性能更佳。其一体现在计算结果更加接近真实值，能更加精确地模拟复杂非线性物理问题，其二在于JADE-SVR作为一种机器学习方法，将回归分析的全过程交予计算机，省去大量人工工作量。

一般的机器学习方法有可能过高的估计回归模型的复杂程度，从而发生“过拟合”现象。SVR理论上用结构风险最小化策略代替传统的经验风险最小化策略，使之较传统机器学习方法具有更好的泛化性能，在编程实现上利用交叉验证进行参数寻优，进一步降低了出现“过拟合”的可能。本文选用试验数据样本数量在200～300区间内，从数据分析的结果来看，SVR模型给出的预测精度并没有显著低于拟合精度，故而没有出现“过拟合”的现象，这说明JADE-SVR对本文涉及的开孔沉箱波浪反射系数、垂直力折减系数的回归分析是适用的。

4 结论

传统回归分析方法，在拟合回归公式之前还要进行单变量分析，从而一一确定各变量的影响阶数，这一过程是人工完成的，有一定的随意性，为了保证拟合公式的泛化性能，通常将各变量的影响阶数确定的较低，偏于保守。利用本文建立的JADE-SVR模型对开孔沉箱反射系数、垂直力折减系数进行拟合，对比传统多元回归分析法可以发现，JADE-SVR模型对拟合精度和泛化性能都有所改进，可以利用其对波浪-开孔沉箱相互作用问题进行深入研究。

随着科技的不断进步和大数据的兴起，各行业的分析研究工作都倾向于依靠更加庞大丰富的试验数据样本。在港口工程领域，数值模拟方法的不断完善也为物理模型试验提供了有益补充，使得数据分析的样本容量大大增加，这样机器学习方法具有的高效率、高精确度的优势将越来越明显。