反激变换器无源耗散型RCD箝位电路分析与设计

汪 礼，何宁业，陈珍海，胡 娟，郭启利

(1．黄山学院 智能微系统安徽省工程技术研究中心，安徽 黄山 245041；2. 广州金升阳科技有限公司，广东 广州 510700)

0 引言

反激变换器拓扑结构简单、成本低廉，在中小功率工业电源中应用非常广泛[1].反激变换器功率MOS管关断瞬间，由变压器漏感产生的电压尖峰可能会导致其雪崩击穿而损坏.为了有效保护功率MOS管，大量文献报道了相关电压箝位电路的分析与设计[2-3].其中无源能量耗散型RCD箝位电路(以下简称RCD箝位电路)由于电路结构简单、设计成本低廉，广泛应用于中小功率反激变换器中.文献[4-7]从RCD箝位电路工作过程中能量守恒的角度提出了相关元器件参数的求解方程.文献[8]在文献[4-7]的基础上提出回馈能耗，进一步完善和丰富了箝位过程中能量守恒的表达式，其最终目的仍然是推导求解RCD箝位电路的元件参数.文献[9]认为反激变压器次级绕组漏感能量对RCD箝位电路也存在影响，进一步修正了箝位过程中能量守恒的表达式.

诸多的文献都是从RCD箝位电路工作过程中能量守恒，推导RCD箝位电路元件参数；但是从抑制尖峰电压的角度出发，应该依据RCD箝位电路参数，从理论上推导计算功率MOS管关断后其漏极电压极值.为此本文详细分析RCD箝位电路工作原理，推导建立功率MOS管关断后其漏极瞬态电压二阶微分方程.从RCD箝位电路工作过程中能量守恒的角度，解析并确定功率MOS管漏极电压取得极值的条件，最终得到只要合理选择RCD箝位电路元件参数Cc和Rc，即可准确地量化功率MOS管关断以后出现的电压极值Vdcmax.并通过试验数据对理论分析和设计过程进行了验证，为反激变换器的设计提供可靠、有效的理论支撑和依据.

1 RCD箝位电路工作过程分析

采用RCD箝位电路的反激变换器结构如图1所示，图中：Rc、Cc、Dc构成RCD箝位电路；Lk为变压器漏感；n为变压器初级绕组和次级绕组之间的匝比；Q为功率MOS管；Coss为功率MOS管输出电容；iDC为RCD箝位电路的回路电流；iP为MOS管关断瞬间的峰值电流.

图1 无源耗散型RCD箝位反激变换器

图2为功率MOS管Q漏极电压Vds，电流iQ以及RCD箝位电路回路电流iDC和箝位电容Cc两端的电压波形.

图2 无源耗散型RCD箝位电路工作波形

为了解析功率MOS管Q关断以后，MOS管漏极电压的瞬态表达式，本文将RCD箝位电路的工作过程分为5个时刻点进行详细的阐述.

1) (t0～t1)：Q在t0时刻截止，变压器励磁电感Lm中的电流开始对电容Coss和输出端二极管结电容Cj进行充电和放电.在t1时刻变压器初级侧，被输出电压箝位为反射电压nVo.在t1时刻之后变压器开始将导通时间内存储的能量传输到输出端.但是存储在漏感中的能量无法转移到次级侧，因此漏感中的电流仍然对Coss充电，直到t2时刻Vds等于Vin+Vcs,然后Dc打开(Vcs为RCD箝位电路电容Cc两端电压的稳态值).

2)(t2～t3)：t2时刻后RCD箝位电路Dc打开，变压器初级绕组电流开始传输到RCD箝位电路中.此阶段RCD箝位电路电容Cc开始充电，该工作过程的等效电路如图3(a)所示.其中Req等效为变压器交流电阻与电路中的寄生电阻之和，理论计算式取10 Ω.

3)(t3～t5)：iDC在t3时刻达到零，此时箝位电容Cc开始放电，但由于二极管的反向恢复需要时间，Dc将继续导通至t5时刻，其等效电路如图3(b)所示.t5时刻结束，RCD箝位电路二极管Dc关断，箝位电容Cc利用并接的电阻Rc继续将二极管导通时存储的能量缓慢地进行释放，直到下一个功率MOS管关断时刻的到来.

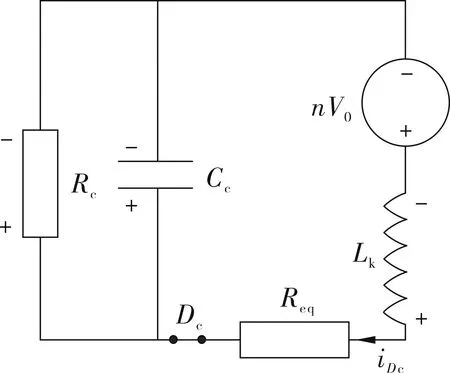
(a) 箝位电容充电等效电路

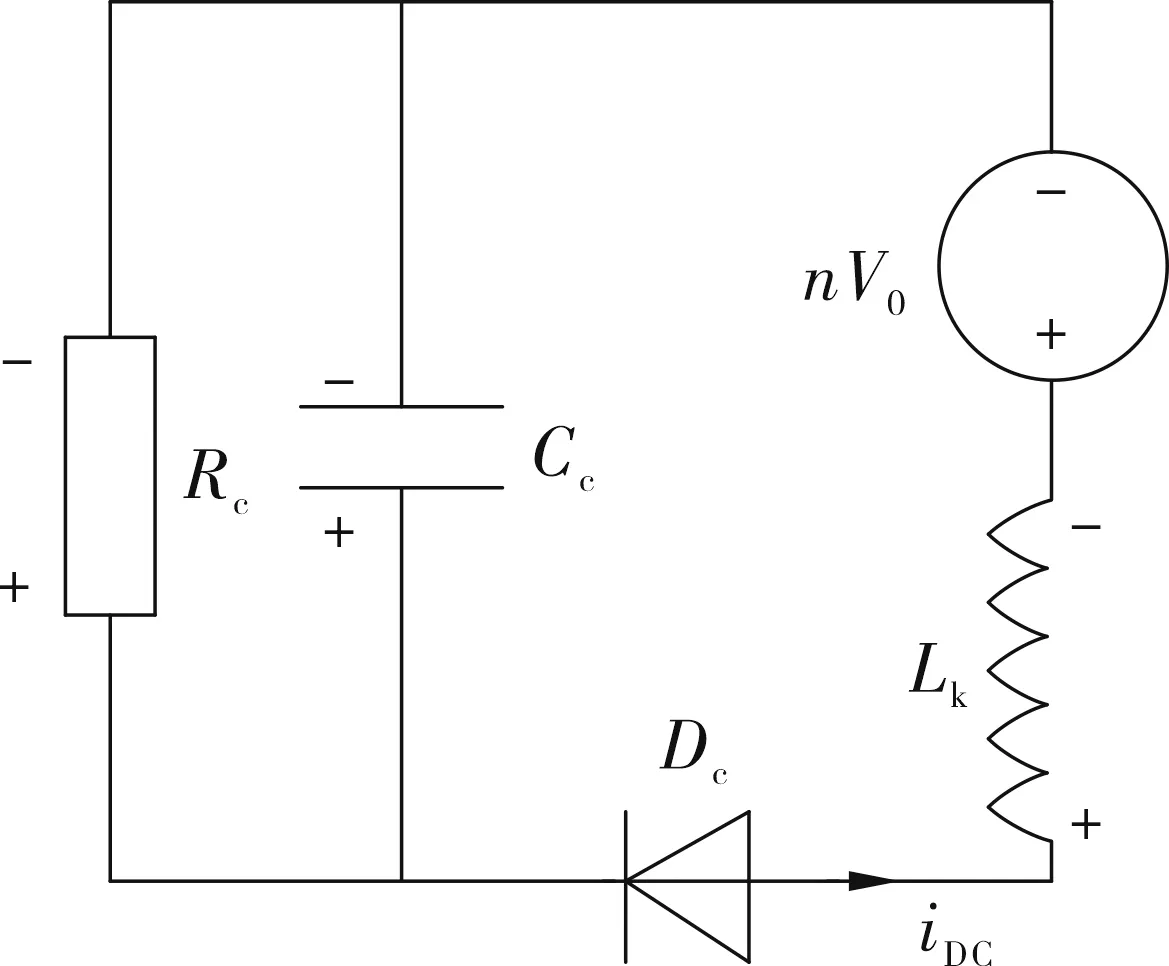
(b) 箝位电容开始放电等效电路图3 RCD箝位电路吸收漏感能量等效电路

RCD箝位电路的工作过程表明了其限制功率MOS管漏极电压极值的本质.功率MOS管关断的瞬间，由于漏感释放能量，假设反激拓扑中未设置任何的尖峰电压箝位电路，漏感仅仅只对MOS管输出电容Coss充电，由于Coss容值极小，充电电压的尖峰瞬间会上升到一个很大的值.如果在电路中增加RCD箝位电路，电压上升到Vin+Vcs以后，箝位电路开始工作，箝位电容Cc比Coss的容值要大得多，利用电容Cc的充电过程延缓了电压上升的斜率，从而限制了功率MOS管的关断瞬间漏极电压的上升.

2 功率MOS管关断瞬间漏极电压极值方程推导

由图2可知，功率MOS管漏极电压的极值出现在RCD电容Cc充电到最大值的时刻.因此依据图3(a)电容Cc的充电等效电路建立瞬态电压的二阶微分方程，即可解析功率MOS管漏极电压的极值.

依据基尔霍夫电压定律(KVL)箝位电容Cc两端电压的时域二阶微分方程为

(1)

初始条件Vc(t2)以及dVc(t2)/dt表达式为

Vc(t2)=Vcs,

(2)

(3)

二阶微分方程的解Vc(t)为

(4)

其中，

(5)

wd=

(6)

(7)

(8)

式(5)中阻尼系数b是寄生电阻和箝位电路放电周期的RcCc倒数的相关表达式，是一个很小的值.因此Vc(t)在t3时刻的最大值近似为

(9)

即

Vdcmax=Vcmax+Vinmax+VDC,

(10)

式中：Vinmax为反激变换器交流输入电压最大值，经整流滤波后的直流峰值一般取375 V；VDC为箝位电路二极管Dc的压降，一般取0.5～0.7 V，实际情况下可忽略不计.

因此求解功率MOS管关断瞬间漏极电压的极值，实际为求解RCD箝位电容Cc两端电压的极值.由式(9)可以看出，Vcmax是电容Cc两端电压稳态值Vcs和箝位电路元件参数Cc和Rc的函数.因此只要合理地确定Vcs的值，即可在给定的元件参数Cc和Rc的条件下，近似计算功率MOS管关断瞬间漏极电压的极值.

3 箝位电容Cc两端电压稳态值Vcs的确定

反激变换器功率MOS管关断后，反射电压nVo在漏感电流下降期间对RCD箝位电路做功形成的反射能耗Wr将直接影响变换器的工作效率.因此，首先需要明确反射能耗Wr和箝位电容稳态值Vcs之间的关系.根据图3(a)以及KVL得到漏感两端的电压值为

VLk=Vcs-nV0.

(11)

则漏感电流的峰值ip(t)瞬态表达式以及其下降到零的时间Δt为

ip(t)=ip-VLk·t/Lk,

(12)

Δt=ip·Lk/(Vcs-nV0).

(13)

由于功率MOS管的输出电容COSS非常小，近似认为反射电压nVo在漏感电流下降期间只对RCD箝位电路做功[10].因此反射能耗Wr为

(14)

针对式(14)进行求导得

(15)

Wr和Vcs的关系曲线如图4所示. 由图4可知，当Vcs的值大于反射电压nVo时，Wr急剧减小.为了尽可能地减小Wr，Vcs不仅要大于nVo，还要尽可能地增大.但是从式(9)可以看出，Vcs增加将导致功率MOS管漏极电压极值也随之增大，因此需要寻找约束Wr取值尽可能小的限制条件.

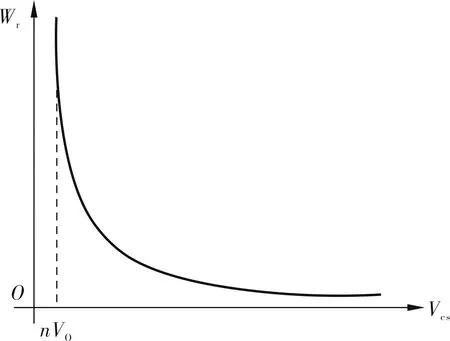
图4 Wr和Vcs关系曲线

RCD箝位电路吸收的能量除了反射能耗以外，还包括漏感本身提供的能量，漏感提供的能量WLk为[11]

(16)

反激变压器漏感一般为励磁电感的1%～5%之间，其数量级一般在几百个nH.中小功率反激变换器输入端的峰值电流ip为几十到几百mA之间，因此漏感提供的能量非常小.

反射能耗Wr如果小于漏感提供的能量WLk，仍然继续减小反射能耗Wr对改善反激变换器的工作效率变得微乎其微[12].因此将Wr和WLk相等作为限制Wr继续减小的条件，即

Wr=WLk,

(17)

Vcs=2·nV0.

(18)

由以上分析可知，当箝位电容Cc的稳态值Vcs取2倍nVo时，可以合理地在反激变换器工作效率和功率MOS管漏极电压极值之间进行折衷.

4 RCD箝位电路元件参数的计算

箝位电容Cc两端电压的稳态值Vcs确定以后，即可计算RCD箝位电路总的功率耗散，即

(19)

式(19)中，当反激变换器工作于电流连续模式(CCM)，在最大输入电压以及满载条件下功率MOS管漏极的峰值电流ip为

(20)

当反激变换器工作于电流断续模式(DCM)， 在最大输入电压以及满载条件下功率MOS管漏极的峰值电流ip为

(21)

RCD箝位电路在功率MOS管关断后的t2～t3时间段内吸收的总功率PLOSS都将耗散在缓冲电阻Rc上，缓冲电阻Rc的功率耗散值为Vcs2/Rc，因此RCD箝位电路缓冲电阻Rc的计算表达式为

(22)

箝位电容Cc的大小可以根据电容的电压纹波值与电容放电的电流进行计算，通常情况下ΔV取2%～5%倍Vcs，则

(23)

RCD箝位电路的二极管Dc没有固定的型号要求，一般选取标称值为1 A，反向耐压为1 000 V的超快速恢复二极管即可.

5 试验分析

搭建采用RCD箝位电路反激变换器的试验实例，其主体电路如图1所示.反激变换器输入电压范围为85～265 V AC，输出功率为5 V/5 A，变压器初次级绕组匝比为9，开关频率为45 kHz.经实际测试变压器初级电感量Lm为718 μH,漏感Lk为17.95 μH，反激变换器在满载范围内始终工作在电流连续模式.

测试不同箝位电路参数条件下反激变换器功率MOS管漏源电压波形，并且利用VISO软件将多个VDS波形进行整合，如图5所示.从测试波形可以看出,随着箝位电容Vcs取值逐渐增大1.5nVo到4.0nVo，功率MOS管两端电压Vds逐渐上升.

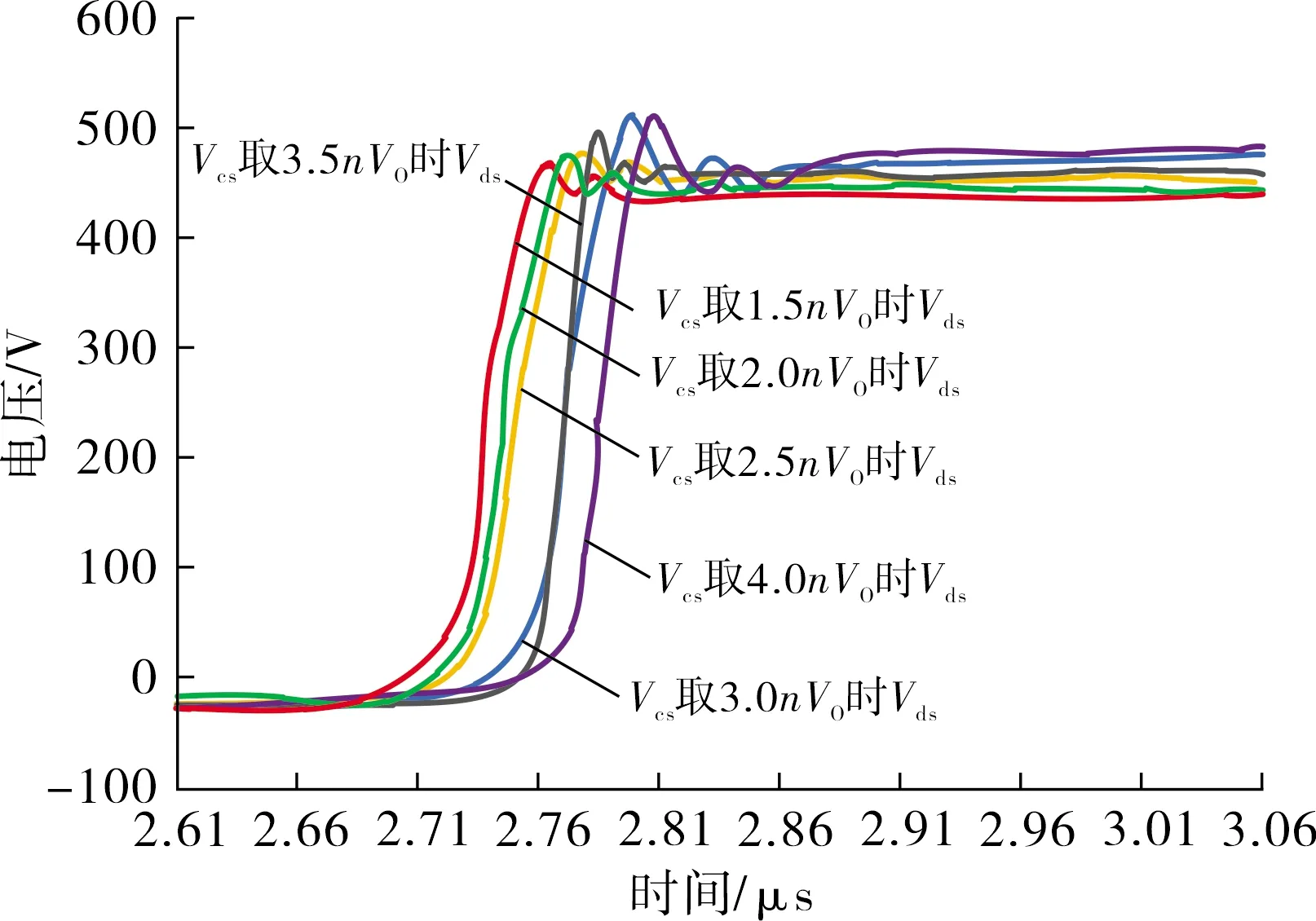
图5 不同Vcs条件下Vds的波形

依据前文分析的结论，依据式(10)计算功率MOS管漏极电压极值时，需要确定RCD箝位电路稳态条件下箝位电容Cc两端电压Vcs的大小，进而通过式(22)～(23)求得RCD箝位电路元件参数Rc和Cc的大小.理论计算和实际测试结果如表1所示.

表1 MOS管漏极极值Vds测试与计算结果

试验数据分析如下：

1) 随着Vcs的增加，反激变换器工作效率增加，在漏感和其他参数不变的前提条件下，反映了反射能耗Wr的减小，符合图4理论推导的结论.

2) 随着Vcs的增加，功率MOS管Vdcmax理论计算值与实际测试值均呈现出增大的趋势，但是二者之间的差距逐渐增大.由于变换器的工作过程中包含了大量的寄生参数，RCD箝位电路吸收的能量实际小于发射能耗Wr和漏感能量WLk理论计算之和，也间接导致了箝位电容Cc两端稳态电压Vcs取值偏大，因此功率MOS管漏极电压极值理论计算值大于实际测试值；另外，当Vcs取值较小时，代表反射能量较高，电路中寄生振荡的可能性更大，此时实际测试值大于理论值.

6 结论

1) 本文建立的开关管漏极电压瞬态二阶微分方程式(10) 极值求解的3个条件，在式(18)和式(22)～(23)均给出了理论的推导和计算.因此，本文的理论分析和公式推导实现了反激变换器功率MOS管关断瞬间漏极电压极值的量化计算，同时搭建的试验案例也充分证明了理论计算的合理性.

2) RCD箝位电路的设计是在箝位电容稳态电压Vcs和变换器工作效率以及元器件参数之间进行折衷，严格意义上没有最优的方案.需要工程设计人员依据工程案例的需求进行合理的选择，表1的相关参数也说明了这一点.例如，如果特别注重反激变换器的工作效率，即可适当增加功率MOS管选型成本，提高功率MOS管漏源电压的耐压值，选取更大的箝位电容稳态电压Vcs.