城市地下空间轨道交通结构抗震性能分析

高伟豪

(淮北师范大学 美术学院，安徽 淮北 235000)

0 引言

随着越来越多的城市建设地下轨道交通，城市地下空间轨道交通结构(以下简称地下交通结构)地震问题受到广泛的关注[1-2].寻求有效方法分析地下交通结构的抗震性能，具有重要应用意义.以往国内外研究人员对地下交通结构抗震性能分析的研究较多，但均存在一定缺陷，例如：文献[3]采用反应位移法计算地震荷载作用下地下交通结构内的土层相对位移与结构上的等效荷载，构建有限元模型计算结构各点的相对位移，分析过程中忽略了边界的处理，分析结果误差高；文献[4]根据结构动力学相关研究结果，分析竖向地震条件下，双层双跨地下结构上下2层中柱的动力响应，该方法只能分析中柱的抗震性能，实用性较差；文献[5]仿真地基结构半无限性过程中选择粘弹性局部人工边界，参考各超越概率水平下的地震动参数，兼顾相位随机性作用，构建地基与结构相互作用的三维有限元模型，未考虑建筑材料对地下交通结构抗震性能的影响，分析结果不全面.

为提高地下交通结构抗震性能分析的准确性，本文采用新方法分析地下交通结构抗震性能，通过Midas/Gtsnx软件构建交通结构的三维有限元动力模型，采用该模块模拟分析地震情况下轨道交通结构的三维数值，依据分析结构研究地下交通结构的地震响应特性.

1 地下交通结构抗震性能分析方法

1.1 工程概况

某地下交通结构工程由地铁1号线车站、2号线车站、街道下穿隧道和其城市地下空间结构组成，地下结构共3层，每一层建筑面积5.2万m2[6].1号线站厅层及地下商业开发设置在地下1层，1号线和2号线的车站站台层分别设置在地下2层和3层，同时地下2层和3层也作为地下停车场使用.2条轨道线路换乘区域在水平视图内为“T”形.下沉式广场在地下1层顶板上开口部位，共设置4处.轨道交通结构覆土层厚度3 m，以箱型框架结构为地下交通结构的结构形式，该结构由众多纵横梁与中柱组成，选取桩筏基础为整体基础型式[7].顶梁、底梁和中梁的基础尺寸分别是1 450 mm×1 850 mm、2 350 mm×2 350 mm和1 050 mm×1 050 mm，中柱大部分采用ø1 150 mm与ø1 350 mm两种型号，采用ø2 000 mm的桩，其长度为30 m.该轨道交通结构地下空间的顶层板、中层楼板、底层板厚度分别为750、450、1 250 mm.

1.2 三维有限元动力模型

通过Midas/Gtsnx软件构建交通结构的三维有限元动力模型，模拟分析得到其地震响应特性[8].设定交通结构三维有限动力模型的长、高、宽分别为645、565、125 m，模型节点119 000，单元个数521 000.在模型内将土地划分为4层，通过四面体单元实施仿真，地层呈现为成层水平图相，表1为土体物理力学参数.分别选取板单元和梁单元仿真交通结构主体和交通结构的梁、柱、桩[9]，表2为板单元与梁单元参数.

表1 土体物理力学参数

表2 结构物理力学参数

1.2.1 材料及参数设定

该轨道交通结构所在区域的软土受地震荷载影响后非线性特征明显，动剪应变增加可减少动剪切模量，通过Davidenkov模型描述二者之间联系[10]，可得

(1)

(2)

式中：Hd和Hmax为动剪切模量与其最大值；ηd为动剪应变；δ和δmax为阻尼比与最大阻尼比；A、B、ηt、θ均为拟合参数.

按照场地土的剪切波可知最大动剪模量为

Hmax=ρws2，

(3)

式中：ρ和ws分别为质量密度和剪切波速.

在剪切波速无法获取的情况下，可采用式(4)计算，即

(4)

1.2.2 边界处理

三维模型内通过人工边界处理应力波，保障模型边界内应力波不会形成发射现象[11].运算静荷载时，两侧边界限制水平向位移，底部边界限制竖向位移，顶部边界为无限制；动力荷载与静荷载运算的不同之处在于两侧边界设置为自由场边界.设置人工边界节点法向的弹簧元件和切向的阻尼元件，提升同有限元法融合采用的便利性[12].弹簧系数包括竖向和水平2种类型[13]，运算方程分别为

(5)

(6)

式中：α为系数，通常为1；Ms、Mh分别为介质边界竖向的截面积、水平方向的截面积；P为介质弹性模量.

单位面积阻尼系数包含压缩波和剪切波2种[14]，运算方程分别为

(7)

(8)

式中：ρ为介质密度；λ为Lame系数；G为介质剪切模量；cw、cx分别为压缩波、剪切波三维面积阻尼系数；Z为人工边界节点的面积.

1.2.3 地震动输入及介质阻尼

根据该轨道交通结构所在区域地震动参数小区划研究结果，经由LSSRL地震反应软件运算得到三维有限元动力模型的地震动输入[15]，最大加速度为0.75 m/s2.

通常情况下，土介质阻尼比为0.05，自振频率d的表达式为

(9)

式中：ws′、Q分别为土层的平均剪切波速和总厚度.

2 试验分析

为测试本文提出的地下交通结构抗震性能分析新方法的性能，试验分别从结构层间位移差、合剪力、合弯矩、合轴力、内力平均增加率、分析准确性等方面分析文中交通结构的抗震性能.

2.1 结构层间位移差(角)

在Ⅰ型地震和Ⅱ型地震影响下，本文方法分析所得地下交通结构3个规范断面内结构顶层同底层间的位移差与位移角的统计结果如表3所示.

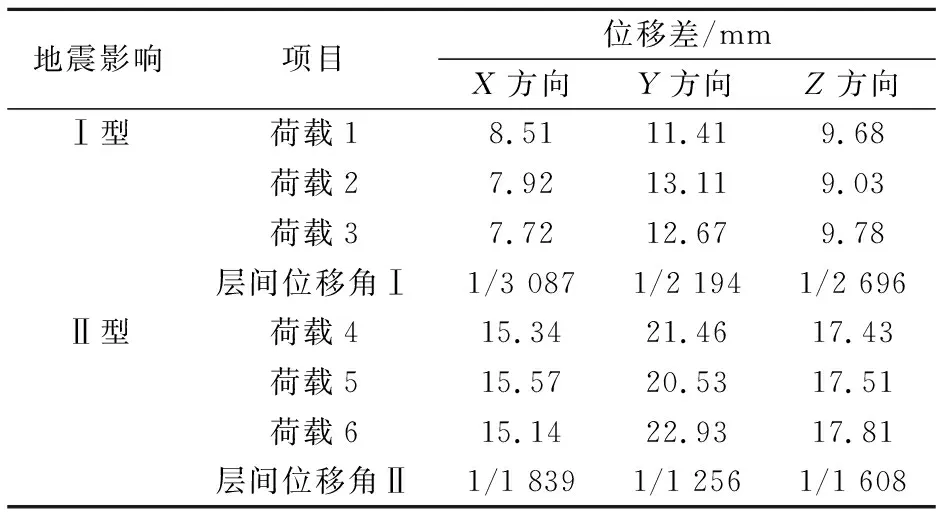
表3 位移差与位移角的统计结果

由表3可得：受Ⅰ型地震和Ⅱ型地震影响，轨道交通结构顶层与底层间位移差的最大值均存在于Y方向；位移差最大值分别为13.11、22.93 mm；层间位移角最大值分别为1/2 194、1/1 256.试验结果表明，本文方法能够有效分析地震影响下地下交通结构的层间位移差和层间位移角.

2.2 结构合剪力分析

受静荷载与地震荷载相结合的影响下，采用本文方法分析地下交通结构不同构件静荷载与地震荷载相结合影响下的合剪力的最大值Qh与单纯静荷载影响下不同构件的剪力Q，比较结果见表4.

表4 不同构件的最大合剪力值比较

由表4可知：在不同荷载影响下，顶层板的最大合剪力值增长率最低，由静荷载影响下的380 kN增长到静荷载与地震荷载相结合影响下的409 kN，其增长率为7.6%；中层板的最大合剪力值增长率最高，由静荷载影响下的63 kN增长到静荷载与地震荷载相结合影响下的113 kN，其增长率为79.4%.试验结果表明，本文方法能够有效分析地震影响下地下交通结构不同构件的最大合剪力情况.

2.3 结构合弯矩分析

受静荷载与地震荷载相结合的影响下，采用本文方法分析地下交通结构不同构件静荷载与地震荷载相结合影响下的合弯矩的最大值Mh与单纯静荷载影响下不同构件的弯矩M，比较结果见表5.

表5 不同构件的最大合弯矩值比较

由表5可知：在不同荷载影响下，合弯矩值增长率最低和最高处分别是顶层板中跨跨中处和右边墙，分别由静荷载影响下的575、746 kN·m上升至静荷载与地震荷载相结合影响下的621、1 497 kN·m，增长率分别为8.0%和100.7%.试验结果表明，本文方法能够有效分析地震影响下地下交通结构不同构件的最大合弯矩情况.

2.4 结构合轴力分析

表6为本文方法分析所得文中地下交通结构受静荷载与地震荷载相结合的影响下，结构不同构件静荷载与地震荷载相结合影响下的合轴力的最大值Nh与单纯静荷载影响下不同构件的轴力N比较结果.

表6 不同构件的最大合轴力值比较

由表6可知：在不同荷载影响下，右边墙的最大合轴力值由静荷载影响下的492 kN增长到静荷载与地震荷载相结合影响下的724 kN，增长率为47.2%，是不同构件中最大合轴力值增长率最高的构件；柱子的最大合轴力值由静荷载影响下的655 kN增长到静荷载与地震荷载相结合影响下的720 kN，增长率为9.9%，是不同构件中最大合轴力值增长率最低的构件.试验结果表明，本文方法能够有效分析地震影响下地下交通结构不同构件的最大合轴力.

2.5 结构内力平均增加率分析

地下交通结构不同构件受静荷载与地震荷载影响下，本文方法分析得出的内力平均增长率的汇总结果见表7.

表7 不同构件内力平均增长率汇总结果

由表7可知：结构不同构件受地震荷载与静荷载影响的剪力相比较，平均增长率达到68.83%；结构不同构件受地震荷载与静荷载影响的弯矩相比较，平均增长率为63.33%；结构不同构件受地震荷载与静荷载影响的轴力相比较，平均增长率为21.00%；结构动力响应导致结构内力增长率较高，进而使结构的抗震性能降低.试验表明，本文方法能够有效分析地震影响下地下交通结构不同构件的内力平均增长率.

2.6 准确性分析

为验证本文方法分析地下交通结构抗震性能时的准确性，分别采用本文方法、基于反应位移法的地下交通结构抗震性能分析方法和基于结构动力学的地下交通结构抗震性能分析方法，分析2.1小节到2.5小节中5种轨道交通结构抗震性能的准确率情况，如图1所示.

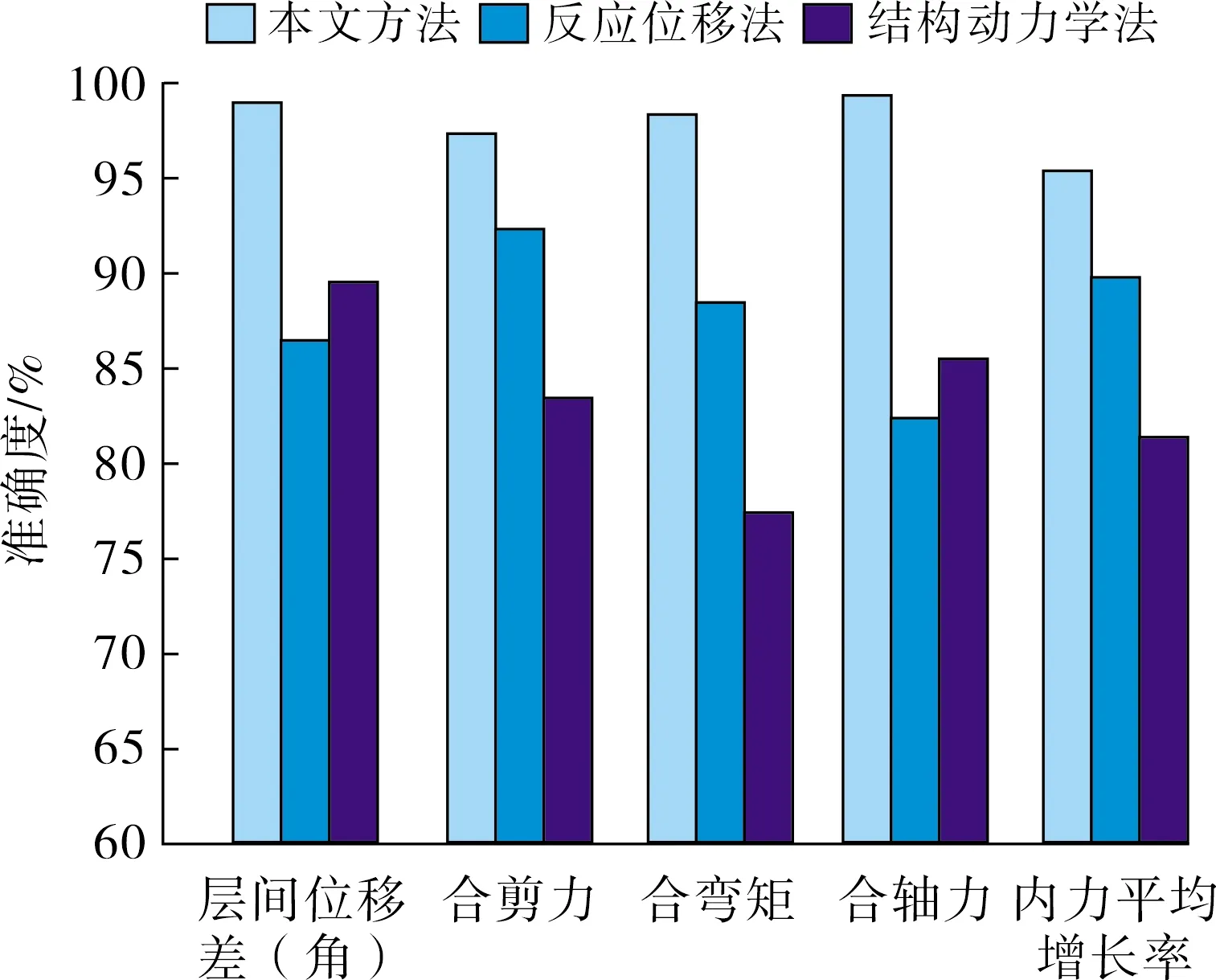
图1 不同方法结构抗震性能分析准确性对比

由图1可知：地下空间轨道交通结构5种抗震性能分析中，本文方法的准确性波动范围为95.3%～99.1%，平均准确度约为97.7%；反应位移法和结构动力学法的准确性波动范围分别为82.4%～92.5%和77.4%～89.2%，平均准确度分别约为88.6%和83.1%.试验结果表明，使用本文方法分析地下交通结构抗震性能具有较高的准确性.

3 结语

当下，地下空间轨道交通方式已经成为多数城市中人们交通出行的首选.由于我国位于地震多发地带，许多地下空间轨道交通建设在高烈度区域内，因此地下交通结构抗震性能问题引起了广泛关注.本文针对反应位移法研究地下交通结构抗震性能时，无法解决有限元模型边界内力波存在严重的发射现象，而存在的抗震性能分析结果误差高的弊端，提出新的地下交通结构抗震性能分析方法.该方法在了解工程概况的基础上，采用Midas/Gtsnx软件构建轨道交通结构的三维有限元动力模型，获取结构的模拟分析三维数值，实现交通结构抗震性能的有效分析.本文方法的优势是利用人工边界处理应力波，保障轨道交通结构三维模型边界内应力波不会形成发射现象，提高地下交通结构抗震性能分析的准确性.