三角恒等变换中的数学思想

■吴淑梅 刘宏博 王 彬

三角恒等变换中蕴含着重要的数学思想,如数形结合思想、分类讨论思想、整体换元思想等,下面举例分析。

一、数形结合思想

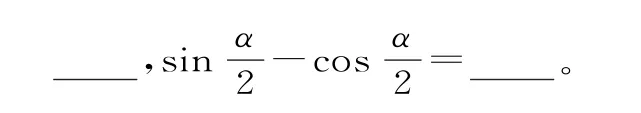
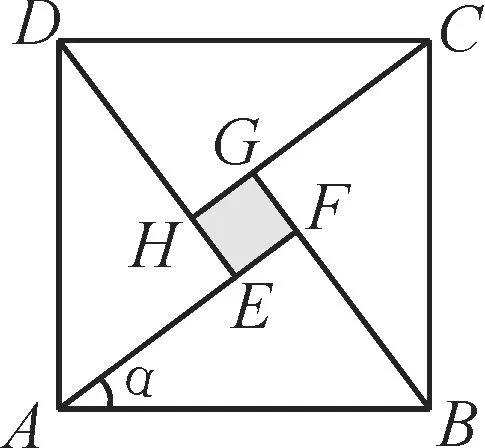
图1

评注：本题以“赵爽弦图”为背景,考查了三角恒等变换中对公式的灵活运用。

二、分类讨论思想

评注：解答本题的关键是准确判断所求角的终边所在的象限。

三、整体换元思想

例3 求函数f(x)=sinx+cosx+sinxcosx,x∈R的最值及取得最值时x的值。

评注：在三角恒等变换中,可以把一个代数式整体视为一个“元”来参与计算和推理,但要注意这个“元”的取值范围。

说明：课题名称:“数学文化”校本课程对学生文化底蕴的培养的研究(立项编号:ayjky20277)。