从三个角度理解机械能守恒定律的应用

■袁兆强

在只有重力或弹力做功的物体系统内,动能与势能可以互相转化,而总的机械能保持不变,这是机械能守恒定律的内容。要想深入理解机械能守恒定律的本质,以达到在具体问题的求解中灵活运用的目的,就需要从以下三个不同的角度着手了。

一、从守恒的角度理解

在满足机械能守恒条件的研究过程中,任意两个状态下,研究对象的机械能必定相等,即E2=E1。通常情况下,我们会选择一个研究过程的始、末两个状态,根据机械能守恒定律列式求解相关物理量。

注意：研究对象在始、末两状态下的机械能相等,不说明研究对象在研究过程中的机械能一定守恒,只有在研究过程中的任意状态下,研究对象的机械能都保持恒定时,研究对象的机械能才是守恒的。

例1 如图1所示,一小球用不可伸长的轻绳悬于O点,小球的质量为m,绳长为l,在O点正下方的B点固定一颗钉子,O、B两点间的距离为d。初始时小球位于与O点同在一水平面上的A点,将其无初速度地释放。为使小球能绕B点做完整的圆周运动,求d的取值范围。

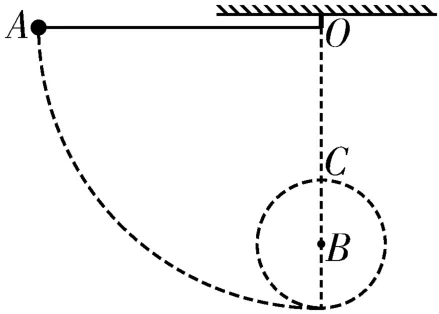
图1

运用守恒的观点根据机械能守恒定律列式求解时,需要选取合适的重力势能的零参考平面,并正确表达研究对象在所选研究过程始、末两状态下重力势能是正,是负,还是零。

二、从转化的角度理解

在满足机械能守恒条件的研究过程中,研究对象动能的增加量等于势能(包括重力势能和弹性势能)的减少量,或者研究对象动能的减少量等于势能(包括重力势能和弹性势能)的增加量,即ΔEk=-ΔEp。

例2 如图2所示是游乐场中过山车轨道的一部分,固定在水平地面上的圆形轨道BCD与右侧弧状轨道AB在B点平滑连接,与左侧弧状轨道DE在D点平滑连接。已知轨道AB最高点A到水平地面的竖直高度h=6.6m,圆形轨道的直径d=1.6m,取重力加速度g=10m/s2,忽略一切摩擦。过山车从轨道AB最高点A无初速度出发,它到达轨道BCD最高点C点时的速度为多大?

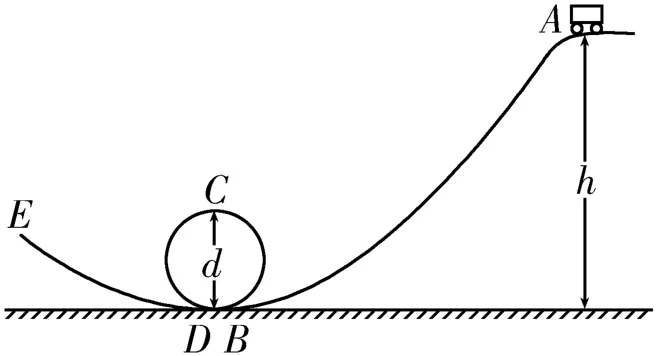
图2

在过山车沿轨道从A点运动到C点的过程中,只有重力做功,机械能守恒。根据机械能守恒定律

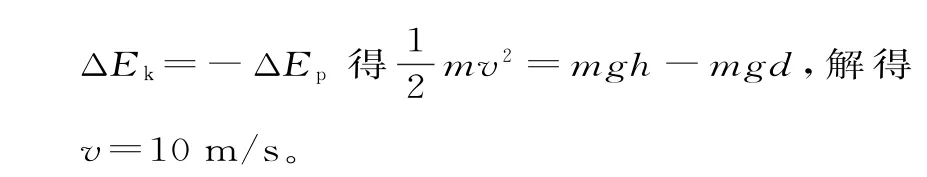
运用转化的观点根据机械能守恒定律列式求解时,无须选取重力势能的零参考平面,只要判断出运动过程中研究对象势能的变化量与动能的变化量即可,解题过程更加简单。

三、从转移的角度理解

在由两个或两个以上的物体组成的系统内,在满足机械能守恒条件的研究过程中,系统某部分的机械能减少了多少,其他部分的机械能就增加了多少,即ΔE1=-ΔE2。

例3 如图3所示,在一光滑水平板的中央有一个小孔,孔内穿过一根光滑轻线,轻线的一端系一质量为M的小球A,另一端系着质量分别为m1和m2的物体B、C,B、C两物体间由一小段轻线相连。当小球A在光滑水平板上沿半径为R的轨道做匀速圆周运动时,B、C两物体都处于静止状态。若将B、C两物体之间的轻线剪断,则小球A的线速度为多大时才能再次在水平板上做匀速圆周运动?

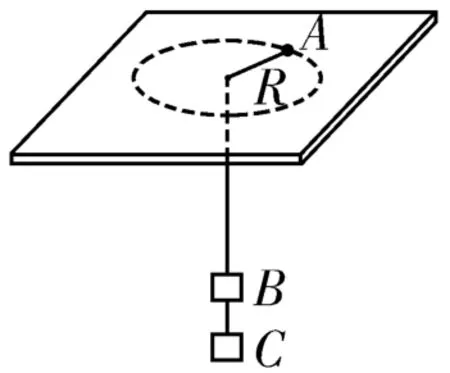
图3

运用转移的观点根据机械能守恒定律列式求解时,需要合理选择满足机械能守恒条件的系统作为研究对象,并正确判断系统内哪些物体的机械能增加,哪些物体的机械能减少。

总结：应用机械能守恒定律解题的基本步骤为选取研究对象(可以是单一物体,也可以是由两个或两个以上物体组成的系统)→根据研究对象所经历的物理过程,进行受力分析和做功分析,判断机械能是否守恒→恰当地选取不同的机械能守恒定律表达式列方程→解方程,代入数据,进行运算,求出结果,并进行检验。

1.如图4所示,在地面上以初速度v0斜向上抛出质量为m的物体,物体落到比地面低h的海平面上。若以地面为零势能参考平面,且不计空气阻力,则下列说法中正确的有( )。

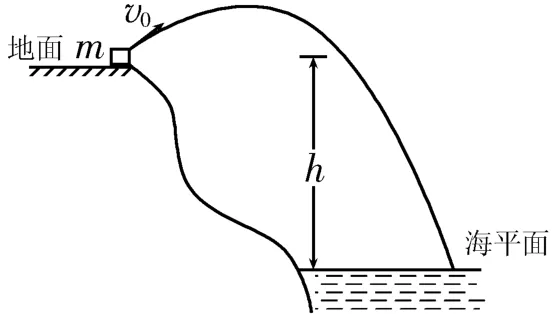
图4

2.如图5所示,长度相同的三根轻杆构成一个正三角形支架,支架的顶点O悬挂在天花板上,并可以绕过O点与支架所在平面垂直的固定轴转动。在支架的顶点A处固定质量为2m的小球,在顶点B处固定质量为m的小球。开始时轻杆OB与地面相垂直,放手后支架开始运动。在不计任何阻力的情况下,下列说法中正确的是( )。

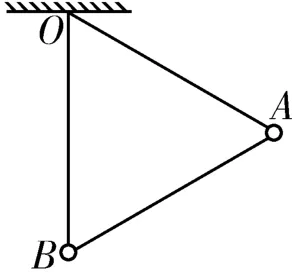
图5

A.固定在顶点A处的小球到达最低点时的速度为零

B.固定在顶点A处小球机械能的减少量等于固定在顶点B处小球机械能的增加量

C.固定在顶点B处小球向左摆动所能到达的最高位置应高于固定在顶点A处小球的起始高度

D.当支架从左向右回摆时,固定在顶点A处的小球一定能回到起始高度

3.如图6所示,质量相等的物体A、B用跨过两个轻小定滑轮的细绳相连,处于静止状态。现将质量与A、B两物体相同的物体C挂在水平段细绳的中点P,挂好后让物体C由静止开始下落。设两滑轮间的距离为2l,细绳足够长,求物体C下落的最大高度。

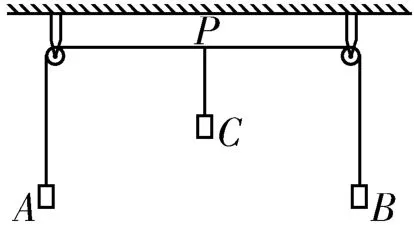
图6

参考答案：