Ground States to the Generalized Nonlinear Schrdinger Equations with Bernstein Symbols
2021-06-29JinmyoungSeokandYounghunHong
Jinmyoung Seokand Younghun Hong
1 Department of Mathematics,Kyonggi Univeristy,Suwon 16227,Korea
2 Department of Mathematics,Chung-Ang University,Seoul 06974,Korea
Abstract. This paper concerns with existence and qualitative properties of ground states to generalized nonlinear Schr¨odinger equations (gNLS) with abstract symbols.Under some structural assumptions on the symbol,we prove a ground state exists and it satisfies several fundamental properties that the ground state to the standard NLS enjoys.Furthermore,by imposing additional assumptions,we construct,in small mass case,a nontrivial radially symmetric solution to gNLS with H1-subcritical nonlinearity,even if the natural energy space does not control the H1-subcritical nonlinearity.
Key Words: Generalized NLS,solitary waves,variational methods,Bernstein symbols.
1 Introduction
We consider the generalized nonlinear Schr¨odinger equation (NLS for abbreviation) of the form


In this article,we are concerned with the ground state solution to the generalized NLS(1.1). By a ground state,we mean a standing wave solution of the form

which minimizes the value of the action integral. A rigorous definition of a ground state shall be given in Section 4. As for the standard NLS,i.e.,the caseP(λ)=λ,inserting the standing wave ansatz(1.2)into(1.1),we get the standard stationary NLS

In this case, the theory of ground states has been almost completed during several decades. A criteria for their existence and nonexistence, depending on the range ofµandp, is established in [1,22,23]. Qualitative properties of ground states, such as positiveness,radial symmetry,monotonicity,and uniqueness have been proved in[4,13,14].
With a general symbolP,the stationary generalized NLS is given by

In this paper,we are interested in finding general conditions on the symbolPwhich allow ground states to the generalized NLS (1.4) to have the same kinds of qualitative properties. We propose the following structural assumptions for the symbolP:
(H1)P:[0,∞)→[0,∞)is continuous on[0,∞)and smooth on(0,∞);
(H2)Pis a Bernstein function,i.e.,P′is totally monotone(see Section 2 for definition);

Our first theorem states that by assuming(H1)–(H3),one can construct a ground state to(1.4)that fulfills desired qualitative properties.
Theorem 1.1(Existence of a ground state).Suppose(H1)–(H3).Let p ∈(1,(d+s)/(d −s))be given. Then for anyµ>0,the generalizedNLS

possesses a ground state u ∈HP+µwhich is positive,radially symmetric and monotone decreasing in the radial direction.
The sign-definiteness of a ground state is naturally expected for the original NLS as a result of Hopf maximum principle enjoyed by second order elliptic PDEs. Here, we show that the minimizing property of a ground state and the strict positiveness of the fundamental solution of the operatorP(−Δ)+µgives the same consequence.
Theorem 1.2(Sign-definiteness of a ground state).Suppose(H1)–(H3). Let p ∈(1,(d+s)/(d −s))be given and u ∈HPµ be a ground state to(1.4).Then u0is either positive everywhere or negative everywhere.
The radial symmetry of a ground state is usually shown by the moving plain method [13] for standard NLS or by strict Riesz rearrangement inequality [17] for fractional NLS and pseudo-relativistic NLS.These methods do not seem to work without the explicit form ofP. As for uniqueness,a standard argument requires spectral information for the linearized operator at the ground state(see[4]). In[16],Lenzmann showed by a perturbative method that a(radial)ground state to pseudo-relativistic nonlinear Hartree equations (NLH for abbreviation) is unique for the small mass case. In [8], the authors developed,in a similar point of view,some perturbative arguments that show the uniqueness,up to a translation,of a(possibly non-radial)ground state to higher-order NLH.In the same spirit,we are able to show the symmetry and uniqueness of a ground state under more restrictive assumptions onPandpwhenµis sufficiently small. More precisely,we require that

We note that the choices ofP(0)=0 andP′(0)=1 in(H4)are just for numerical simplicity. Indeed,the assumption(H4)can be relaxed to
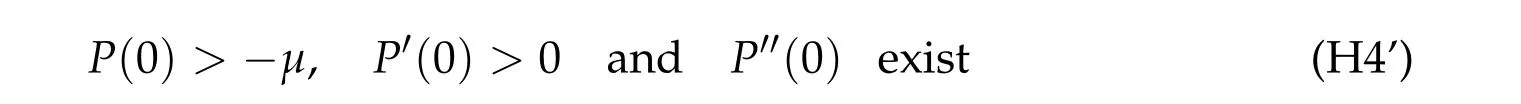
by a simple reformulation of Eq.(1.4).
Theorem 1.3(Uniqueness of a ground state).Suppose(H1)–(H4). Let p ∈(1,d/(d −s))be given and u ∈HPµ be a positive ground state to(1.4). Then there exists µ0> 0such that ifµ∈(0,µ0)then u is unique up to a translation.
The uniqueness result asserted in Theorem 1.3 is perturbative in nature. Indeed,the smallness of the massµis transferred to the smallness of∊>0 in the equation plays an indispensable role in the proof.



Theorem 1.4(Existence of a radial solution forH1subcritical range ofp).Suppose(H1)–(H4). For any p ∈(1,(d+2)/(d −2))and any q>d/s, there exists µ0> 0such that ifµ∈(0,µ0)then there exists a radially symmetric nontrivial solution u ∈Ws,q(Rd)to(1.4).
The rest of this paper is organized as follows.In Section 2,we introduce the concept of Bernstein functions and the properties of Fourier multiplier operators made by Bernstein symbols. In Section 3, we construct a nontrivial radial solution to (1.4) for small massµ>0 by using perturbation argument. Section 4 is devoted to the study of existence and qualitative properties on ground states to(1.4).
2 Preliminaries
2.1 Bernstein functions
A continuous functionf: [0,∞)→[0,∞)is said to betotally monotoneif it is smooth on(0,∞),and

for all nonnegative integernandλ> 0, wheref(n)is then-th derivative off. Totally monotone functions are an important class of functions in many areas of analysis. We refer the book[21]for a comprehensive overview. As for totally monotone functions,an important theorem is Bernstein’s theorem. It asserts that a totally monotone function is the Laplace transform of a Borel measure.
Theorem 2.1(Bernstein’s theorem[2]).If f:[0,∞)→[0,∞)is totally monotone,then there exists a non-negative Borel measureµon[0,∞)such that

From now on,we assume thatf: [0,∞)→[0,∞)andf′is totally monotone. Such a function is called aBernstein function. Note that the symbols(λ+m2)s −m2s,0 This function space is equipped with the inner product First,we prove that the symmetric decreasing rearrangement reduces the norm. Proposition 2.1(P´olya-Szeg¨o inequality).Suppose that f: [0,∞)→[0,∞)is a Bernstein function. Then,for any non-negative function u ∈Hf(Rd;R),we have where u∗is the symmetric decreasing rearrangement of u. Proof.We claim that iffis a Bernstein function,thene−f(λ)is totally monotone. For the claim,it suffices to show that then-th derivative ofe−f(λ)is of the form(−1)ne−f(λ)gn(λ),wheregnis a(non-negative)totally monotone function. Whenn=0,it is obviously true withg0= 1. Suppose that the claim holds whenn=k. Then,the next order derivative ofe−f(λ)is(−1)k+1e−f(λ)gk+1(λ),where By functional calculus,we write Note that by the claim and Bernstein’s theorem,for eachs ≥0,there exists a non-negative Borel measureµssuch that Hence, insertingλ=−Δ, we see that the operatore−s f(−Δ)is the convolution of the radially symmetric,non-negative and decreasing function Thus we complete the proof. Next,we prove the symmetry and the positivity of the fundamental solution. Proposition 2.2(Positivity of the fundamental solution).If f: [0,∞)→[0,∞)is a Bernstein function, then the fundamental solutionΦ = Φf for the differential operator f(−Δ)is radially symmetric,strictly positive and decreasing.Proof.It follows from (2.1)and the heat kernel. We also show that a real-valued function inHfcan be orthogonally decomposed into two functions having different signs. Proposition 2.3(Orthogonal decomposition).Suppose that f: [0,∞)→[0,∞)is a Bernstein function. Then, for any u ∈ Hf(Rd;R), there exist u± ∈ Hf(Rd;R)such that u=u+−u−,u± ≥0a.e. and〈u+,u−〉Hf(Rd;R)=0. Proof.LetKbe the set of non-negative functions inHf(Rd;R),which is a closed convex non-empty cone inHf(Rd;R). Then, by Theorem 3.4 in [12] (see [19] for the original work),there exists a unique decompositionu=u1+u2,withu1∈Kandu2∈K∗,such that〈u1,u2〉Hf(Rd;R)=0,whereK∗is the dual cone ofKdefined by It remains to show that everyw ∈K∗is non-positive. Indeed,ifu ∈C∞c(Rd;R)is nonnegative,then by Proposition 2.2,so is Φ∗u. Therefore,for anyw ∈K∗,we have However,sinceuis arbitrary,this proves thatwis non-positive. Here we recall the structural assumptions for the symbolP: (H1)P:[0,∞)→[0,∞)is continuous on[0,∞)and smooth on(0,∞); (H2)Pis a Bernstein function,i.e.,P′is totally monotone; (H4)P(0)=0,P′(0)=1 andP′′(0)exists. The advantage of assuming (H2) is to provide a nice integral representation of the symbol from which several important properties in our analysis are deduced. Lemma 2.1(Integral representation of the symbol).Suppose that the symbol P:[0,∞)→Rsatisfies(H2). Then,there exists a unique measureµon[0,∞)such that As a consequence,if we further assume(H4),then the zeroth and the first moments of the measure is finite and Proof.By the fundamental theorem of calculus,we have By(H2),it follows from Bernstein’s theorem for complete monotone functions[21,Theorem 1.4]that for some unique measureµon[0,∞). Therefore,inserting the integral formula forP′(λ)and then integrating inℓ,we obtain(2.2). By(H2),the symbolPis sub-linear,and differentiation reduces the degree of the symbol. Lemma 2.2(Properties of the symbol).Suppose that P:[0,∞)→Rsatisfies(H2). (i) For all λ1,λ2≥0,we have P(λ1+λ2)≤P(λ1)+P(λ2). (ii) For any integer k ≥0and λ ≥0,we have|P(k)(λ)|λ−kP(λ). Proof.(i)By(2.2),we have (ii)Differentiating(2.2)ktimes,we write and then apply the elementary inequality Thus we complete the proof. This section is devoted to prove Theorem 1.4. Consider a one-parameter family of nonlinear elliptic equations whereP∊(λ) =P(∊λ)/λ. IfP′(0) exists, Eq. (3.1) formally converges to the nonlinear elliptic equation We remark that Eq.(3.1)is possibly supercritical,since the differential operator may have a lower order than the Laplacian(see Lemma 2.2(i)). In this section, we impose the hypotheses (H1)–(H4) on the symbolPto establish existence of a non-trivial solution to (3.1) by the contraction mapping argument in [6]provided that∊is sufficiently small. The following two lemmas will be employed in the contraction mapping argument.The first lemma asserts a certain coercivity of the Fourier multiplierP∊(−Δ). Lemma 3.1(Coercivity).Suppose that(H1)–(H3)hold for some s ∈(0,2]. Letµ> 0. Then,for any1 where‖·‖L(Lq;Ws,q)denotes the standard operator norm from Lq to Ws,q. Proof.By the H¨ormander-Mikhlin theorem,it suffices to show that for all integerk ≥0, withj1+···jm=k. We prove the claim by induction. The zeroth step is trivial. If the claim is true for thek-th step, then the (k+1)-th step follows, because when the derivative hits one of the fractions,it generates fractions of the same kind. Precisely,we have The second lemma claims the convergenceP∊(−Δ)→−Δ in the norm resolvent sense. Lemma 3.2(Norm resolvent convergence ofP∊).Suppose that(H1)–(H4)hold for some s ∈(0,2]. Letµ>0. Then,for any1 Proof.By the H¨ormander-Mikhlin theorem again,it suffices to show that and by(3.4),we have It is obvious that and we have shown that (see(3.4)). Thus,it remains to consider the last factor(λ −P∊(λ)). Indeed,differentiating(2.2)and using(2.3),one can show that Therefore,collecting all,we complete the proof of(3.7). Now,we seek for a solution of the form near the ground state to the limit equation. Note that Theorem 3.1 below obviously includes Theorem 1.4. Theorem 3.1(Existence and local uniqueness of a non-trivial solution).Suppose that(H1)–(H4)for some s ∈(0,2]. Assuming(3.3),let u0be the unique radially symmetric solution to the limit equation(3.2). Then,there exists small ∊0>0such that Eq.(3.1)has a non-trivial radially symmetric solution u∊∈Ws,q for all r ≥2. Moreover, u∊is a unique radial solution in the neighborhood of u0with respect to the norm‖·‖Ws,q. We insertu∊=u0+w∊,assuming that the differencew∊is small. Then,reorganizing in the linearized form,the equation forw∊is derived as We claim that the linearized operator on the left hand side is invertible. Lemma 3.3(Invertibility of the linearized operator).Suppose that(H1)–(H4)hold for some s ∈(0,2]. Then,for any q ∈[2,∞),there exists small ∊0> 0such that if0<∊≤∊0,then the operator Proof.We write where Therefore, is invertible onLqr, and its inverse is uniformly bounded. Therefore, inverting(3.9)and applying Lemma 3.1,we complete the proof. We aim to find a solution to (3.10) by a contraction mapping argument. The following elementary inequality is helpful to handle the nonlinearity in the equation. Lemma 3.4.If a>0and p>1,then Proof.By the fundamental theorem of calculus, If 1 we obtain the desired bound. Ifp> 2, we apply the fundamental theorem of calculus again to get Therefore, there exists small∊0> 0 (depending on the functionu0) such that for∊∈(0,∊0], while ifp>2, Collecting all, we conclude that Φ is contractive onBδ(0). Therefore, Eq. (3.10) (consequently,(3.1))has a unique solution inBδ(0). In this section we prove Theorems 1.1–1.3. Throughout this section,µdenotes a positive constant. For a symbolPsatisfying(H1)–(H3),we consider the Hilbert spaceHP+µ=HP+µ(Rd;R).We note thatP+µis a Bernstein function because so isP. By(P2)and Sobolev embedding,one has a natural embedding Then the functionalIgiven by is well-defined andC1onHP+µ. It is clear that (1.4) is the Euler-Lagrange equation of(4.1). We sayu0∈HP+µis a ground state to(1.4)ifu0is a critical point ofIandI(u0)≤I(v)for any nontrivial critical pointv ∈HP+µofI. In this subsection,we construct a ground state for the generalized NLS,which is positive,radially symmetric and monotone decreasing up to translation. We shall be done by establishing existence of a minimizer for the variational problem Such a minimizer is of course a ground state for the generalized NLS,since every critical point ofIsatisfies the constraint. The following lemma is trivial, but we write it as a lemma, because it will be used frequently. Lemma 4.1.Suppose that u is admissible for the variational problem(4.2),i.e.,u/=0and We assume that Then,there exists t ∈(0,1]such that t˜u is admissible and If we further assume that either the inequality(4.3a)or(4.3b)holds strictly,then Proof.Since there existst ∈(0,1]such thatt˜uis admissible,i.e., Therefore,by(4.3a),it follows that If either(4.3a)or(4.3b)holds strictly,thent<1 andI(t˜u) Proof of Theorem1.1.By the constraint, for admissibleu. Let{un}∞n=1⊂HP+µbe a minimizing sequence. For eachn, applying Proposition 2.3, we writeun=un,+−un,−such thatun,± ∈HP+µ,u± ≥0 and〈un,+,un,−〉HP+µ= 0. We define a new sequence{˜un}∞n=1by ˜un=un,++un,−≥|un|.Then,we have Thus,it follows from Lemma 4.1 that there exists{tn}∞n=1⊂(0,1]such that{tn˜un}∞n=1is also a minimizing sequence. Replacingunbytn˜un,we assume thatunis nonnegative. Letu∗n, wheref∗is the symmetric decreasing rearrangements off ≥0. Then, by P´olya-Szeg¨o inequality(Proposition 2.1)and the measure preserving property of the rearrangement, Hence,by Lemma 4.1 again,we can find a sequence{tn}∞n=1⊂(0,1]such that{tnu∗n}∞n=1is also a minimizing sequence. Replacingunbytnu∗n,we assume thatunis radially symmetric and monotone decreasing. We now have a minimizing sequence{un}∞n=1of nonnegative radially symmetric functions monotone decreasing in the radial direction. Hence,passing to a subsequence,{un}weakly converges to someuinHP+µ,which implies that and{un}converges toua.e. This shows thatuis also nonnegative radial symmetric function monotone decreasing in radial direction. This implies a positive lower bound of‖un‖HP+µ, which makes a contradiction. Thus,choosing appropriatet ∈(0,1]by Lemma 4.1 as above,we can maketuadmissible,and Therefore,we conclude thattuis a minimizer. We once more redefiningtuasuso thatuis a nonnegative ground state to(1.4)which is radially symmetric and decreasing in radial direction. It remains to show thatuis strictly positive everywhere. Let ΦP+µbe the fundamental solution of the differential operatorP(−Δ)+µ. By Proposition 2.2,it is strictly positive. Since the ground stateuis represented by we see thatuis strictly positive. This completes the proof. This subsection is devoted to prove Theorem 1.2,the sign-definiteness of a ground state to(1.4). Proof of Theorem1.2.By Proposition 2.3,there are non-negativeu± ∈HP+µsuch thatu=u+−u−,〈u+,u−〉HP+µ= 0. We observe thatu+(x)u−(x) = 0 for allx ∈Rd. In other words,u+andu−have disjoint supports, Indeed,if(4.4)does not hold,the function ˜u=u++u−obeys‖˜u‖2HP+µ=‖u‖2HP+µand where the inequality holds strictly due to cross terms. Thus, it follows from Lemma 4.1 that there existst ∈(0,1]such thattuis admissible andI(tu) Next,we claim that To prove the claim,we note that by(4.4),the equality holds in(4.5).As a consequence,the function ˜udefined previously is also a minimizer, so it is a solution to (1.4). Moreover,˜u=|u|. For contradiction, we assume thatu+/= 0 andu−/= 0. Observe from the orthogonality ofu+andu−that Then either The strict inequality is due to the assumption thatu−/= 0. Sinceuis a minimizer, this makes a contradiction and the claim is proved. Finally, we have already seen in the proof of Theorem 1.1 that a nonnegative (nonpositive) minimizer is positive (negative)everywhere since the fundamental solution ΦP+µofP+µis strictly positive. This ends the proof. Here, we prove Theorem 1.3. Throughout this subsection, we assume(H1)–(H4)on the symbolPhold. We fix arbitrarily chosenp ∈(1,d/(d −s))and denote byu0the unique radial positive ground state to the original NLS, As mentioned in Section 3,the generalized NLS is equivalently transformed to Lemma 4.2(Convergence).Let v∊∈HP∊+1be a positive ground state to(4.9). Then there exists{a∊}⊂Rd such that Proof.The lemma is a natural consequence of energy minimality of the ground statesv∊to(4.9). We refer to Proposition 2.3 in[8],with which their proof follows the exactly same lines. We omit the proof for avoiding the paper too lengthy. Lemma 4.3(Nondegeneracy).Let {v∊} ⊂HP∊+1be a family positive ground state to(4.9)such that{v∊}converges to u0in HP∊+1as ∊→0. Define the linearized operator by Then there exists a constant β>0independent of small ∊>0such that for any g ∈HP∊+1which is HP∊+1orthogonal to ∂xiv∊for each i=1,···,d. Proof.This lemma can be proved in the same spirit with Lemma 3.3 but one should take care on the change of function spaces from the radial function space (Ws,qr →span{∂xiv∊|i= 1,···,d}⊥). This can be easily done by repeating the proof of Proposition 3.3 in[8]. We omit it. Proof of Theorem1.3.Let{v∊},{˜v∊} ⊂HP∊+1be two families of positive radially symmetric ground states to (4.9). By Lemma 4.2, we may assume that both of{v∊}and{˜v∊}converge tou0inHP∊+1as∊→0 by taking translations if necessary. This means that Let{a∊}⊂Rdbe a family of vectors such that Then one has since We redefine ˜v∊(·−a∊)by ˜v∊so that ˜v∊is still a ground state, ˜v∊−v∊is orthogonal to∂xiv∊inHP∊+1and lim∊→0‖v∊−˜v∊‖HP∊+1=0 by definition ofa∊. Let us definer∊= ˜v∊−v∊. From Eq.(4.9),one has so that by Lemma 4.3, It is easy to see from (H3) that there exists a uniform constantC> 0 independent of∊∈(0,1)such that Then we invoke Lemma 3.4 and H¨older inequality to obtain Combining this with(4.16)and using the fact that lim∊→0‖r∊‖HP∊+1=0,we getr∊=0 for sufficiently small∊>0. This shows ˜v∊=v∊and ends the proof. Acknowledgements This research of the first author was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT(NRF-2020R1A2C4002615). This research of the second author was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF)funded by the Ministry of Science and ICT(NRF-2020R1C1C1A01006415)


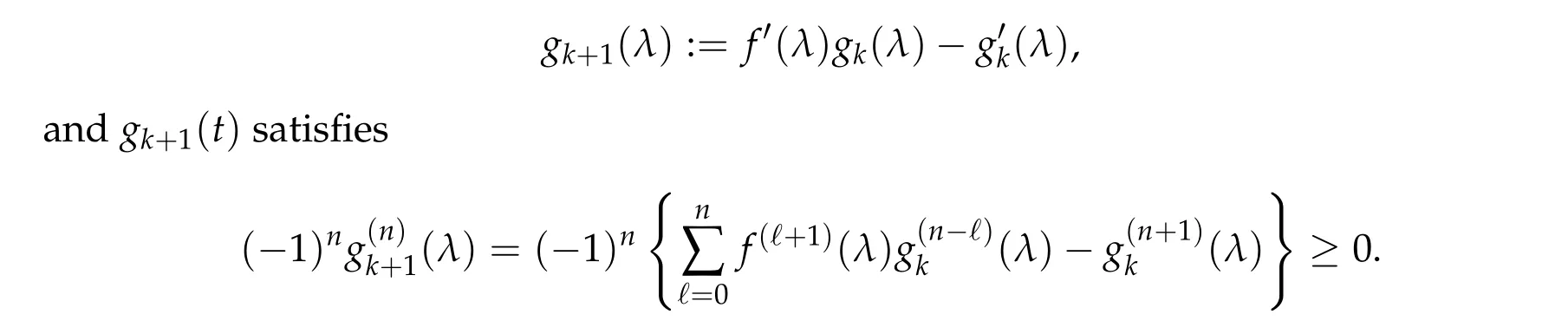
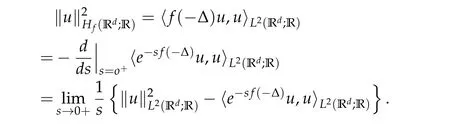





2.2 Assumptions on the symbol P and its properties







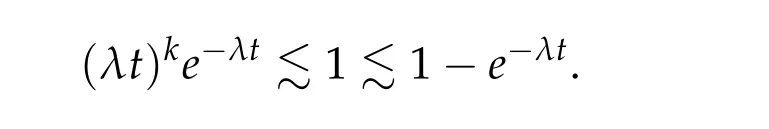
3 Construction of a radial solution to the generalized NLS in H1 subcritical range of p








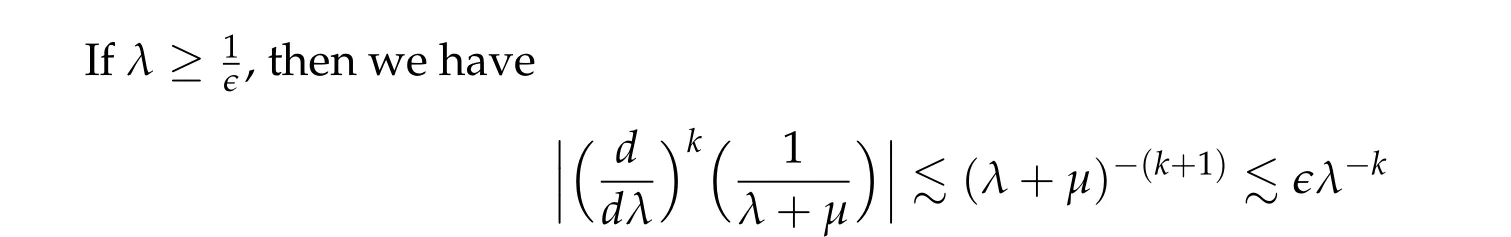




3.1 Construction of a non-trivial solution









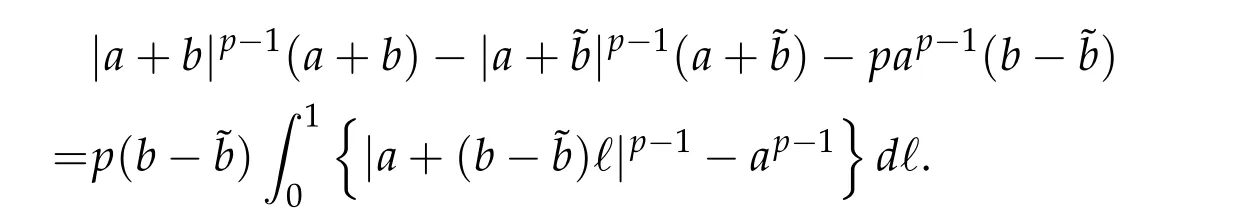







4 Ground state for the generalized lower-order NLS
4.1 Variational settings
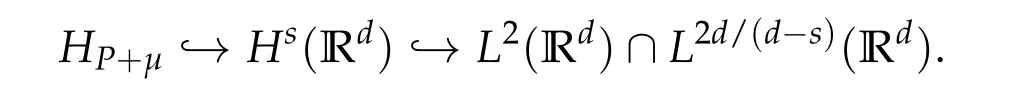

4.2 Existence of a ground state






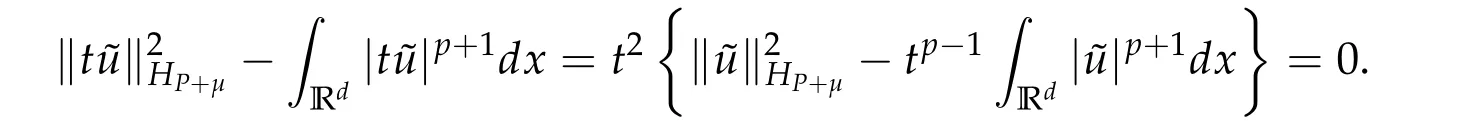
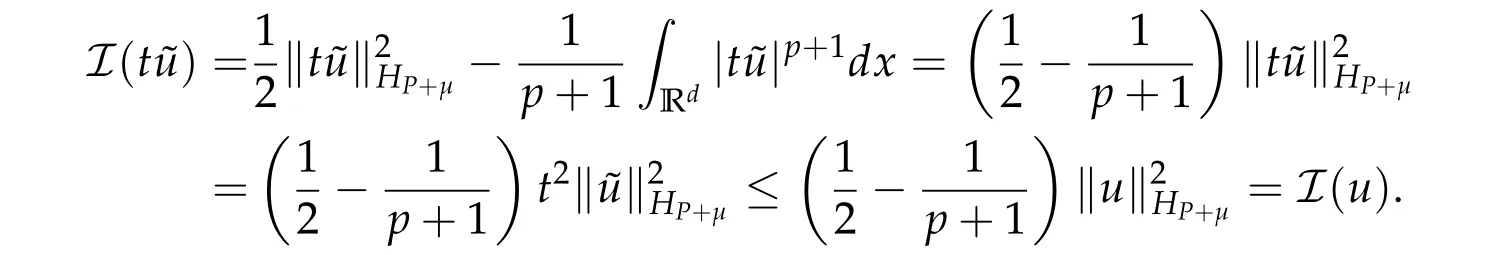


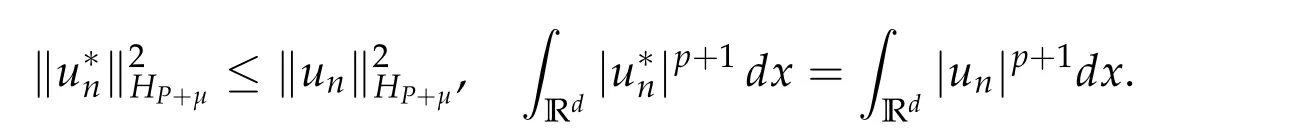




4.3 Sign-definiteness of a ground state





4.4 Uniqueness of a ground state


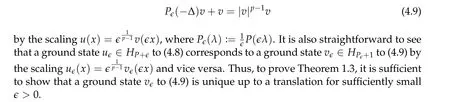
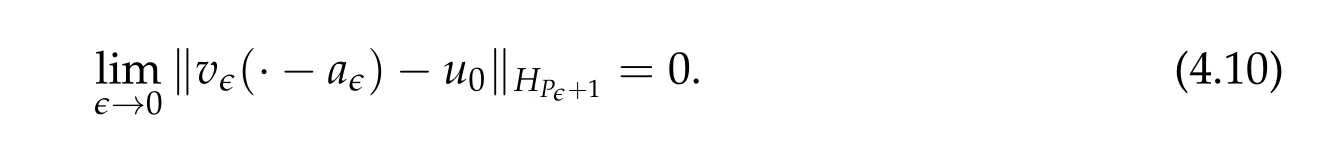





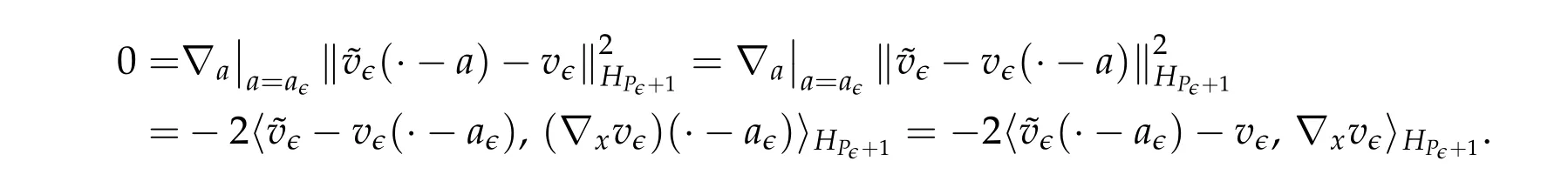




杂志排行
Analysis in Theory and Applications的其它文章
- Classification of Positive Ground State Solutions with Different Morse Indices for Nonlinear N-Coupled Schr¨odinger System
- Index Iteration Theory for Brake Orbit Type Solutions and Applications
- Diffusion with a Discontinuous Potential: a Non-Linear Semigroup Approach
- Deformation Argument under PSP Condition and Applications
- Multiple Sign-Changing Solutions for Quasilinear Equations of Bounded Quasilinearity
- Ground States to the Generalized Nonlinear Schr¨odinger Equations with Bernstein Symbols
