Index Iteration Theory for Brake Orbit Type Solutions and Applications
2021-06-29ChungenLiuYimingLongandDuanzhiZhang
Chungen Liu,Yiming Long and Duanzhi Zhang
1 School of Mathematics and Information Science,Guangzhou University,Guangzhou,Guangdong 510006,China
2 Chern Institute of Mathematics and LPMC, Nankai University, Tianjin 300071,China
3 School of Mathematical Sciences and LPMC, Nankai University, Tianjin 300071,China
Abstract. In this paper, we give a survey on the index iteration theory of an index theory for brake orbit type solutions and its applications in the study of brake orbit problems including the Seifert conjecture and the minimal period solution problems in brake orbit cases.
Key Words: Hamiltonian system,Index theory,Iteration theory,Lagrangian boundary problem,Seifert conjecture,Brake orbits.
1 Introduction
Since 1990,the iteration theory of the Maslov-type index theory for symplectic paths has been systematically developed by Long and his research group[54–56]. It has become a powerful tool in the study of various problems on periodic solutions(or orbits)of nonlinear Hamiltonian systems including: existence, multiplicity, and stability of periodic solution orbits [57,59,67,68] and closed geodesic [5,13,14], stability problems of periodic orbits ofn-body problems [35–37], Rabinowitz’s minimal periodic solution conjecture[12,50–52],Conley’s conjecture on sub-harmonic periodic orbits for second as well as first order Hamiltonian systems[27,32]. Recently,Long,Duan,and Zhu published a survey paper[15]on this topic. Interested readers are referred to this paper and references therein.
Since the paper of[57]of Long,Zhang,and Zhu in 2006,motivated by the study of the existence,multiplicity and stability of brake orbit type periodic solutions of Hamiltonian systems,in order to get more precise information,the index theory and its iteration theory of the Maslov-type index for symplectic paths under brake orbit boundary conditions have been systematically developed. This index and its iteration theory can be used to study brake orbits problems of reversible Hamiltonian systems[47,48,57,73,74]as well as other related problems including Conley conjecture and minimal periodic solution problems in brake orbit case[42,72].
In this survey,we shall give an introduction to this Maslov-type index theory and its relationship with the Maslov index theory in Section 1. In Section 2,we shall describe the main results in the iteration theory of such an index theory. For applications,in Section 3, we shall introduce recent developments on brake orbit problem for compact convex reversible hypersurfaces inR2n, which yields some partial answer to the Seifert conjecture on the multiplicity of brake orbits proposed by Seifert in 1948[64]. In Section 4,we shall briefly summarize the study of the minimal period solution problems of reversible Hamiltonian systems in brake orbit case.
In this paper,letN,R,Z,QandCdenote the sets of natural integers,integers,rational numbers,real numbers and complex numbers respectively. LetUbe the unit circle of the complex planeC,i.e.,U={z ∈C||z|=1}.
2 A review on the Maslov-type index theory iL for symplectic paths under Lagrangian boundary condition
2.1 The iω index theory for symplectic paths
We firstly give the definition ofiωindex for symplectic paths which was first introduced by Long in [54] of 1999, all the materials here with historical notes can be found in [56]of 2002 and the recent survey paper[15]. Let(R2n,ω0)be the standard symplectic vector space with coordinates(x1,···,xn,y1,···,yn)and the standard symplectic form
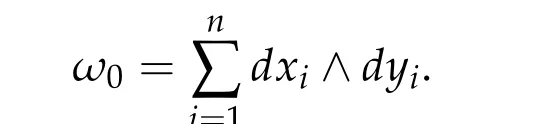
Let
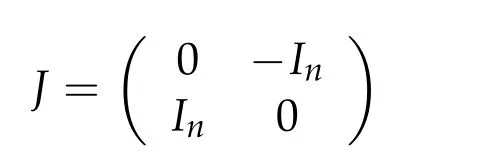
be the standard symplectic matrix, whereInis the identity matrix inRn. The real symplectic group Sp(2n)is defined by
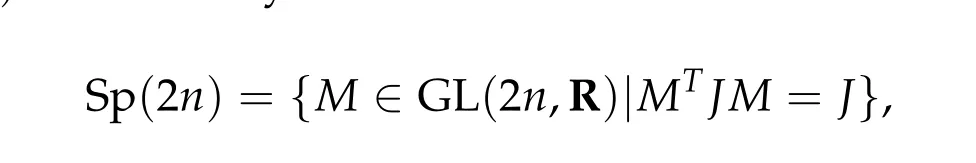
whose topology is induced from that ofR4n2, whereMTis the transpose of matrixM.The set of symplectic paths in Sp(2n)starting from the identity matrix is defined by
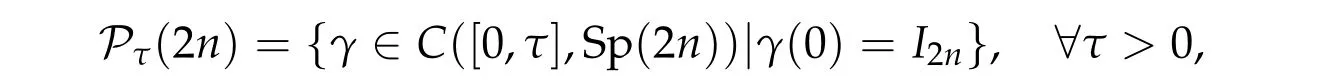
whose topology is induced from Sp(2n). Denote the set of all 2n×2nreal matrices byL(R2n) and its subset of symmetric ones byLs(R2n). For anyM ∈Ls(R2n), we denote the dimensions of the maximal positive definite subspace, negative definite subspace,and kernel ofMbym+(M),m−(M)andm0(M),respectively.
Forω ∈UandM ∈Sp(2n),the function
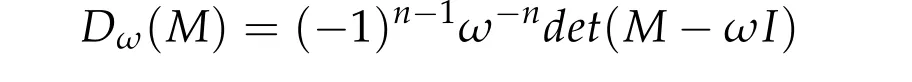
was defined and proved to be real by Long in [53] of 1999. Following [53] and [54], for anyω ∈U,we define
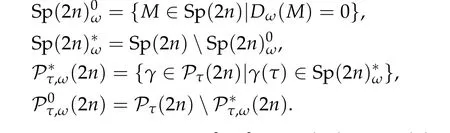
For any two continuous pathsξandη: [0,τ]→Sp(2n)withξ(τ) =η(0),we define their joint path by
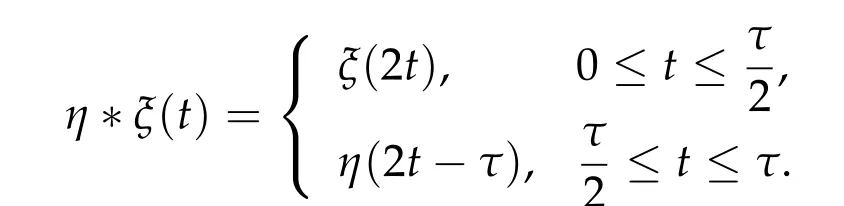
For any two 2ki×2kimatrices of square block form
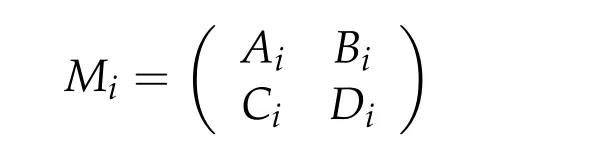
withi= 1,2 as in[56],the◇-sum ofM1andM2is defined by the following 2(k1+k2)×2(k1+k2)matrix
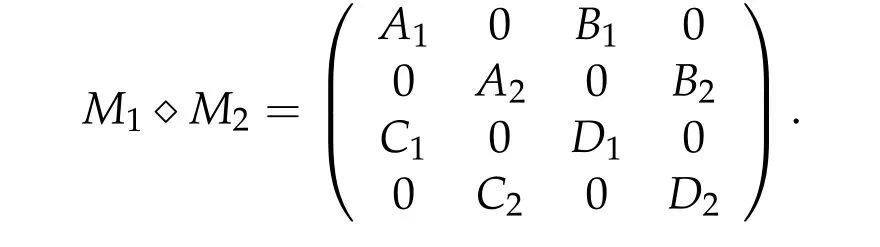
We denote byM◇kthek-time self◇-sum ofMfor anyk ∈N.
Define a special pathξn ∈Pτ(2n)by
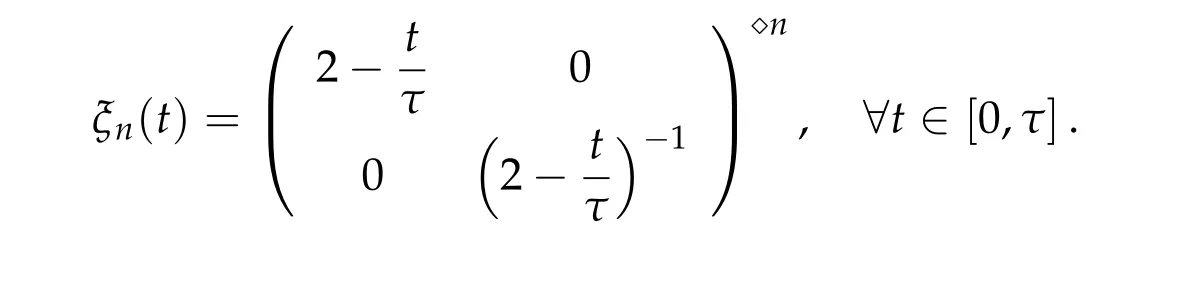
Definition 2.1([54,56]).For any ω ∈Uand M ∈Sp(2n),define
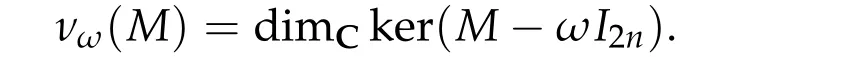
For any τ>0and γ ∈Pτ(2n),let

If γ ∈P∗τ,ω(2n),then we define

where the right-hand side of(2.1)is the usual homotopy intersection number and the orientation of γ ∗ξn is its positive time direction under homotopy with fixed endpoints.
If ω= 1,simply denote by i(γ)instead of i1(γ). If γ(τ)∈P0τ,ω(2n),let F(γ)be the set of all open neighborhoods of γ in Pτ(2n),and define

Then(iω(γ),νω(γ))∈Z×{0,1,···,2n}is called the index function of γ at ω.
For anyM ∈Sp(2n),following[54]we define
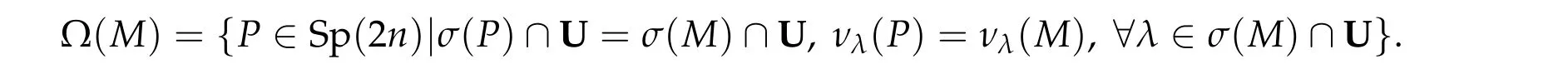
Denote by Ω0(M)the path-connected component of Ω(M)containingM,and call it the homotopy component ofM ∈Sp(2n).
Definition 2.2([54,56]).For any M ∈Sp(2n)and ω ∈U,we define the splitting number of M by

for any path γ ∈Pτ(2n)with γ(τ)=M.
2.2 The Maslov type iL-index theory associated with a Lagrangian subspace for symplectic paths
In this section,we give a brief introduction to the Maslov typeiL-index theory. We refer to the papers[40,41,47,48,57]for more details.
A Lagrangian subspaceLof the standard symplectic space(R2n,ω0)with

is anndimensional subspace satisfyingω0|L= 0. The set of all Lagrangian subspaces in(R2n,ω0)is denoted by Λ(n).
Whenτ= 1, we write simplyP(2n) instead ofP1(2n). For a symplectic pathγ ∈Pτ(2n),we write it in the following form

Since the space Sp(2n)is path connected,and the set ofn×nnon-degenerate matrices has two path connected components consisting of matrices with positive and negative determinants respectively,we denote by

Definition 2.3([40,57]).We define the L0-nullity of any symplectic path γ ∈Pτ(2n)by

with the n×n matrix function V(t)defined in(2.2).
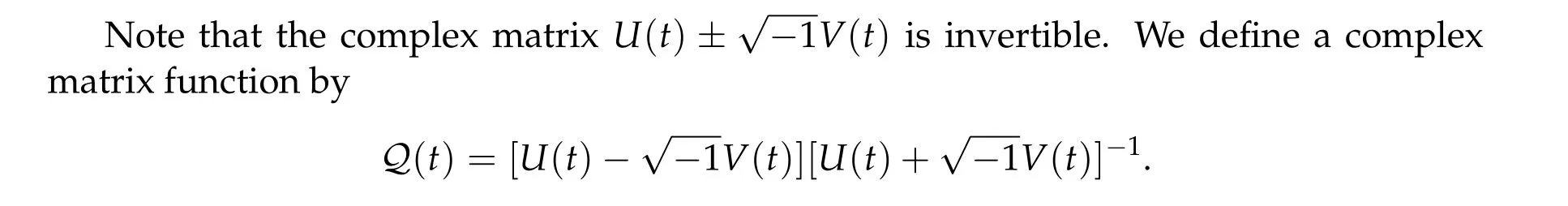
The matrixQ(t)is unitary for anyt ∈[0,τ]. We denote by
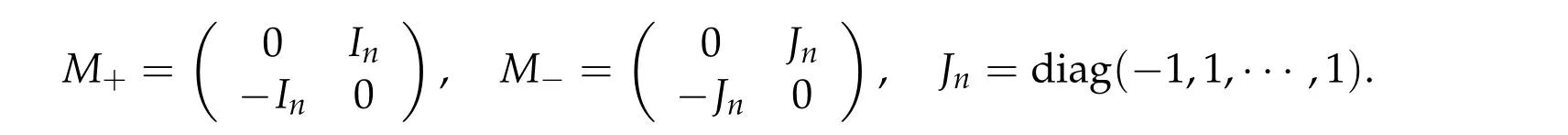
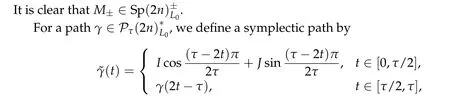

By the definition,we see that the symplectic path ¯γstarts from−M+and ends at eitherM+orM−. As above,we define
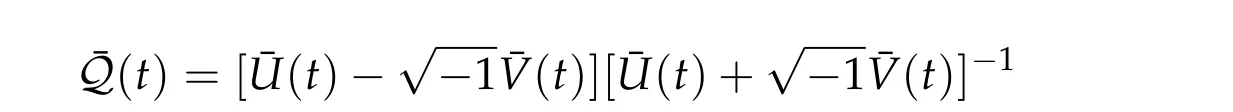
for
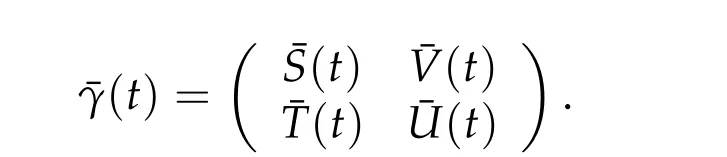
We can choose a continuous function ¯Δ(t)on[0,τ]such that



In the general situation,letL ∈Λ(n). It is well known that Λ(n) =U(n)/O(n),this means that for any linear subspaceL ∈Λ(n),there is an orthogonal symplectic matrix


Definition 2.6([40]).We define the L-nullity of any symplectic path γ ∈Pτ(2n)by
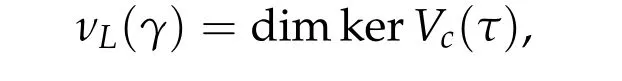
the n×n matrix function Vc(t)is defined in(2.2)with the symplectic path γ replaced by γc,i.e.,

Definition 2.7([40]).For a symplectic path γ ∈Pτ(2n),we define the L-index of γ by
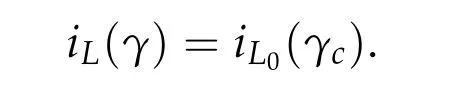
Remark 2.1.(1) The Definitions 2.6 and 2.7 do not depend on the special choice ofP.(2) In [57] of 2006, Long, Zhang and Zhu studied the multiple solutions of the brake orbit problem on a convex hypersurface, they introduced indices (µ1(γ),ν1(γ)) and(µ2(γ),ν2(γ)) for any symplectic pathγ. The indicesµ1(γ) andµ2(γ) are special cases of theL-indexiL(γ) for Lagrangian subspacesL0={0}×RnandL1=Rn×{0}respectively up to a constantn. In[63]of 1993,Robbin and Salamon defined a half integer valued index for symplectic paths with Lagrange boundary conditions.
TheiLindex can also be defined by Maslov indices of the corresponding Lagrangian subspace pair paths.There is a good introduction on Maslov indices of the corresponding real Lagrangian subspace pair paths in[11]of 1994 by Cappel,Lee and Miller,which can be extended to complex Lagrangian subspace pair paths [58]. Recently the first author of this paper defined also aniL-index theory for general symplectic curves in the monograph[43],such an index theory satisfies an axioms characterization in terms of the affine scale invariance,homotopy invariance,path additivity,symplectic additivity,symplectic invariance and normalization.
We denote by
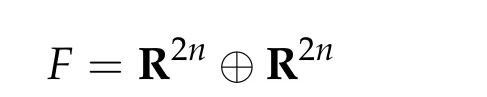
equipped with the standard inner product(·,·)and define the symplectic structure ofFby

We denote by Lag(F)the set of Lagrangian subspaces ofF,and equip it with the topology as a subspace of the Grassmannian of all 2n-dimensional subspaces ofF.
It is easy to check that,for anyM ∈Sp(2n)its graph

is a Lagrangian subspace ofF.
Let

Proposition 2.1([47,59]).For any continuous path γ ∈Pτ(2n),there hold
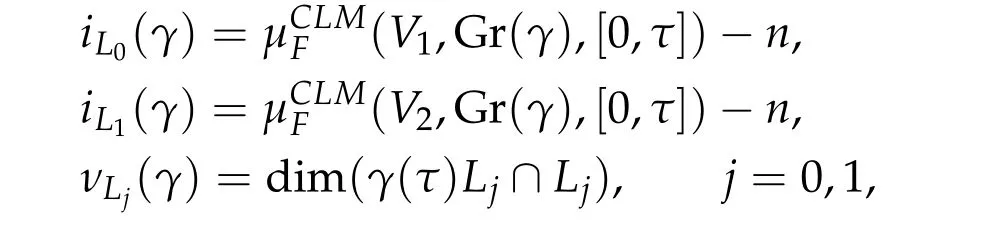
where we denote by iCLMF(V,W,[a,b])the Maslov index for Lagrangian subspace path pair(V,W)in F on[a,b]defined by Cappell, Lee, and Miller in [11]. For any M ∈Sp(2n)and j=0,1,we also denote by νLj(M)=dim(MLj ∩Lj).
In[16],Duistermaat introduced the H¨ormander index which expresses the difference of Maslov index of the same symplectic path under different lagrangian boundary conditions as signature of corresponding quadratic form in nondegenerate case. In [75] of 2018, Zhou, Wu, and Zhu extended the H¨ormander index into degenerate case. By the computation of the H¨ormander index,in[57]of 2006,Long,Zhang and Zhu proved
Theorem 2.1([57]).For any continuous path γ ∈Pτ(2n),there hold
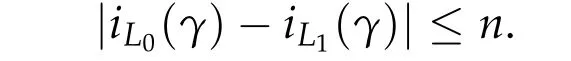
More precisely,for anyP ∈Sp(2n)andε ∈R,set

In[72],Zhang proved
Theorem 2.2([72]).For γ ∈Pτ(2n)with τ>0,we have

wheresgnMε(γ(τ))is the signature of the symmetric matrix Mε(γ(τ))and ε>0is sufficiently small.
We also have,
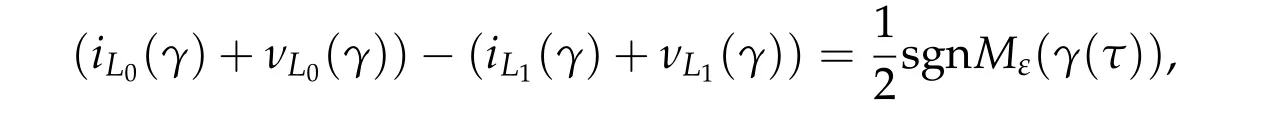
where ε<0and|ε|is sufficiently small.
The key ingredients in the proof of Theorem 3.2 below are some ideas from [47,57]and the following estimate,where the iteration pathγ2will be defined in Section 2 below.
Theorem 2.3([48]).For γ ∈Pτ(2n), let P=γ(τ). If iL0(γ)≥0, iL1(γ)≥0, i(γ)≥n,γ2(t)=γ(t −τ)γ(τ)for all t ∈[τ,2τ],then
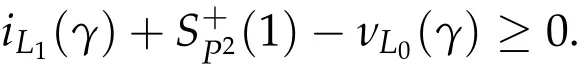
3 The iteration theory for iL0 and iL1 index
In many problems related to nonlinear Hamiltonian systems, it is necessary to study iterations of periodic solutions. In order to distinguish two geometrically distinct periodic solutions,one way is to study the Maslov-type indices of the iteration paths of the fundamental solutions of the corresponding linearized Hamiltonian systems. Forγ ∈Pτ(2n),we define ˜γ(t)=γ(t −j)γ(1)j,j ≤t ≤j+1,j ∈{0}∪N,and thek-times iteration path ofγbyγk= ˜γ|[0,k]for anyk ∈N. In the paper[54]of Long in 1999,the following result was proved
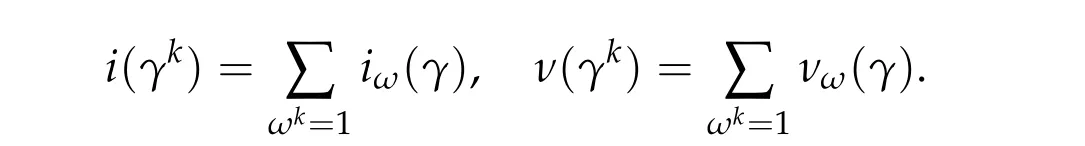
In[55]of 2000,Long established the precise index iteration formula for the Maslov-type indices. From these results, various iteration index formulas were obtained and were used to study the multiplicity and stability problems of periodic solutions related to the nonlinear Hamiltonian systems. We refer to the book[56]of Long in 2002 and the references therein for these topics.
In order to study the brake orbit problem, it is necessary to study iterations of the brake orbits. In order to do this, one way is to study theL0-index of the iteration pathγkof the fundamental solutionγof the corresponding linear system for anyk ∈N. In this case, theL0-iteration pathγkofγis different from that of the general periodic case mentioned above. Its definition is given below.
In 1956, Bott in [10] established the famous iteration formula of the Morse index for closed geodesics on Riemannian manifolds. For convex Hamiltonian systems, Ekeland developed the similar Bott-type iteration index formulas for the Ekeland index theory[17]of 1990. In[54]of 1999,Long established the Bott-type iteration formulas for the Maslov-type index theory. Motivated by the above results, in [47] of Liu and Zhang in 2014,the following Bott-type iteration formulas for theL0-index was established. In[70]of 2018,Wu and Zhu extended the iteration formula to weak symplectic Hilbert spaces.
Define the involution matrix of(R2n,ω0)by
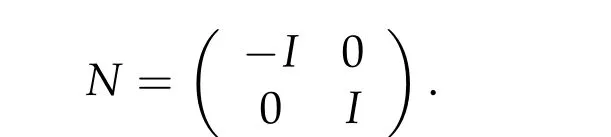
It is anti-symplectic,i.e.,NJ=−JN. The fixed point set ofNand−Nare the Lagrangian subspacesL0={0}×RnandL1=Rn×{0}of(R2n,ω0),respectively.
For simplicity,we supposeγ ∈P1(2n),i.e.,we takeτ= 1. Forj ∈N,we define thej-times iteration pathγj:[0,j]→Sp(2n)ofγby

and in general,fork ∈N,we defineγ(2)=Nγ(1)−1Nγ(1)and

Forγ ∈Pτ(2n),we define

Theorem 3.1([47] of Liu and Zhang in 2014).Suppose γ ∈Pτ(2n), for the iteration symplectic paths γk,when k is odd,there hold

when k is even,there hold
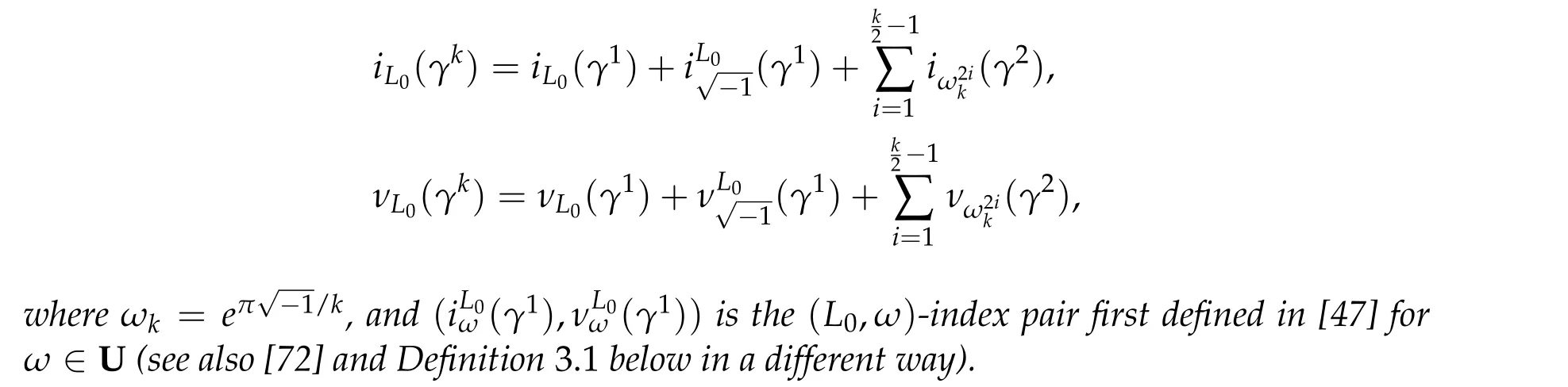
From the Bott-type formulas in Theorem 3.1, the abstract precise iteration index formula ofiL0was given in [47]. We recall the definition ofE(a) = min{k ∈Z|k ≥a}fora ∈R.
Theorem 3.2([47]).Let γ ∈Pτ(2n), γk is defined by as above, and M=γ2(2τ). Then for every k ∈2N−1,there holds
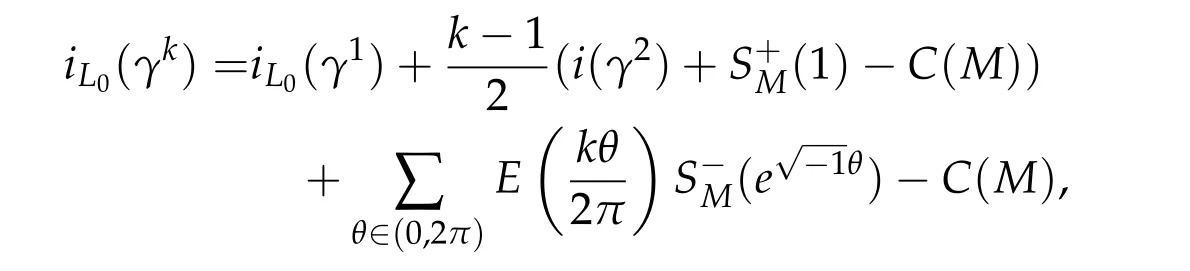
where C(M)is defined by
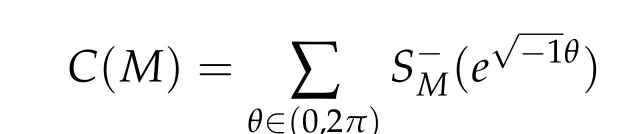
and S±M(ω)is the splitting number of the symplectic matrix M at ω for ω ∈Udefined in Subsection 1.1. For every k ∈2N,there holds


and for even k,we have
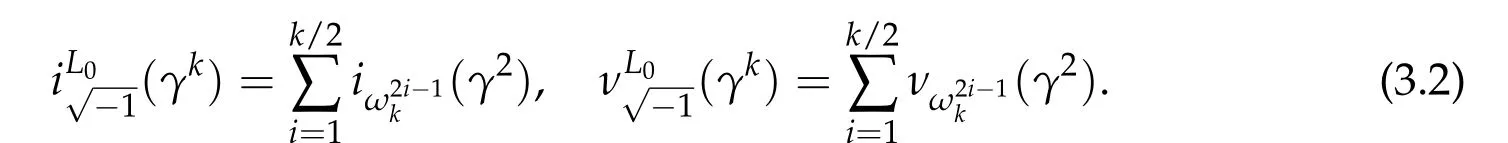
For any given compact strictly convex (or star-shaped)C2hypersurface Σ inR2n, a closed characteristic(τ,y)on Σ is a solution of the problem

wherenΣ(y)is the outward normal vector of Σ atynormalized by the conditionnΣ(y)·y=1. Herea·bdenotes the standard inner product ofa,b ∈R2n.
In the study of closed characteristics problems and closed geodesics,the common index jump theorem[59]of Long and Zhu in 2002 and the enhanced common index jump theorem[13]of Duan,Long and Wang in 2016 for a finite collection of symplectic paths starting from identity with positive mean indicesi1(γj) play important roles. The common index jump theorem of theiL0-index for a finite collection of symplectic paths starting from identity with positive meaniL0-indices was established in[47]. In the following of this paper, we write (iL0(γ,k),νL0(γ,k)) = (iL0(γk),νL0(γk)) for any symplectic pathγ ∈Pτ(2n)andk ∈N. From Theorems 3.1 and 3.2,we know that the mean indices

are well defined and we have
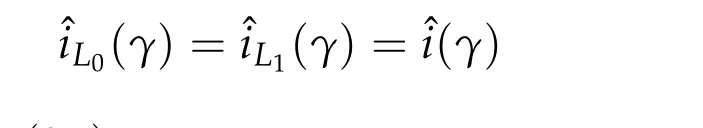
for any symplectic pathγ ∈Pτ(2n).

Then there exist infinitely many(R,m1,m2,···,mq)∈Nq+1such that
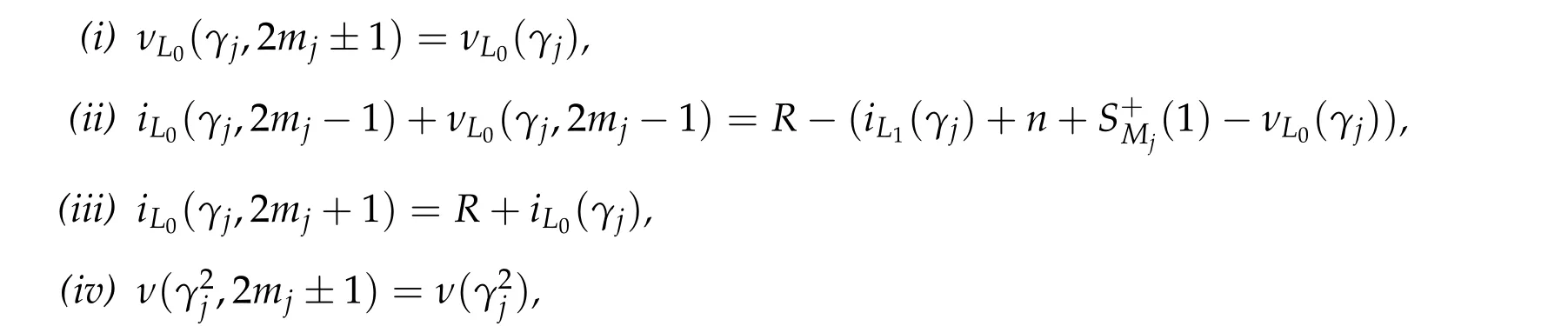
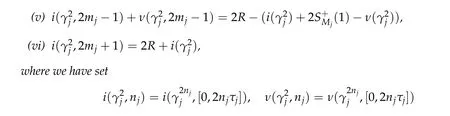
for nj ∈N.
4 Applications, brake orbits on given reversible hypersurfaces in R2n
TheiLindex theory is suitable for studying the Lagrangian boundary value problems(Lsolution,for short)related to nonlinear Hamiltonian systems. A typical application is to study the Seifert conjecture for the multiplicity of brake orbits.
4.1 The Seifert conjecture
Let us recall the famous conjecture proposed byH. Seifert in his pioneer work [64] of 1948 concerning the multiplicity of brake orbits in certain Hamiltonian systems inR2n.We assume thatH ∈C2(R2n,R)possesses the following form
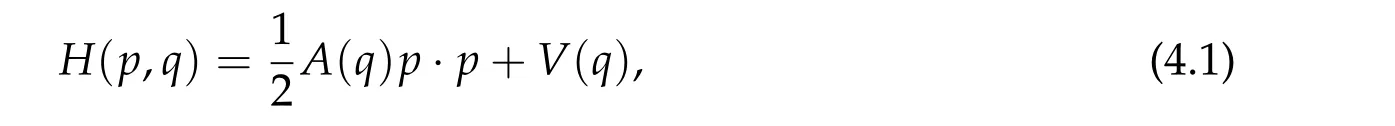
wherep,q ∈Rn,A(q) is aC2positive definiten×nsymmetric matrix inq ∈RnandV ∈C2(Rn,R)is the potential energy. The solution of the following Hamiltonian system
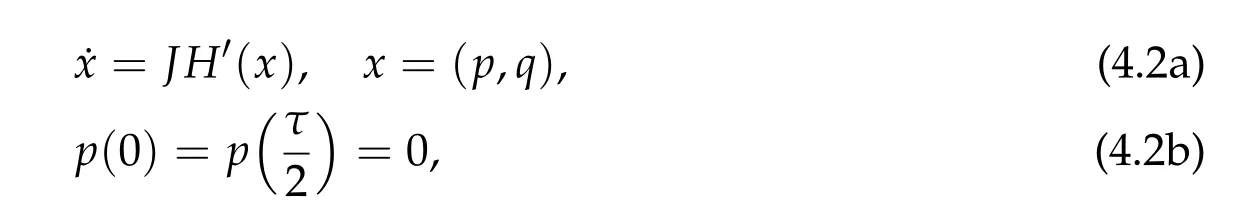
is called a brake orbit. Moreover, ifhis the total energy of a brake orbit (p,q), i.e.,H(p(t),q(t)) =handV(q(0)) =V(q(τ)) =h. Thenq(t)∈¯Ω≡{q ∈Rn|V(q)≤h}for allt ∈R.
In [64] of 1948, Seifert studied the existence of brake orbits for system (4.2a)-(4.2b)with the Hamiltonian functionHbeing in the form of(4.1)and proved that the setJb(Σ)of brake orbits on the energy surface Σ =H−1(h)is not empty,i.e.,Jb(Σ)/= ∅providedV′/=0 on∂Ω,Vis analytic and ¯Ω is bounded and homeomorphic to the unit ballBn1(0)inRn. Denoted by ˜Jb(Σ)the set of geometrically distinct brake orbits on the energy surface Σ. The precise sense of the setsJb(Σ) and ˜Jb(Σ) are explained in the next subsection.Then in the same paper he proposed the following conjecture#˜Jb(Σ)≥nfor Σ described as above.
We note that for the Hamiltonian function
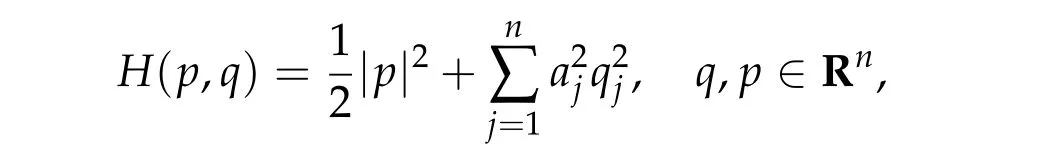
whereai/aj ∈RQfor alli/=jandq=(q1,q2,···,qn),there are exactlyngeometrically distinct brake orbits on the energy hypersurface Σ=H−1(h).
4.2 The generalized Seifert conjecture for reversible hypersurfaces
In general, we suppose thatH ∈C2(R2n{0},R)∩C1(R2n,R) satisfies the following reversible condition
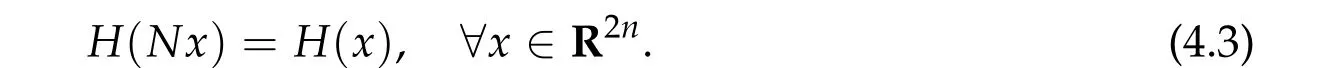
For givenh> 0,we consider the following fixed energy problem of nonlinear Hamiltonian system with Lagrangian boundary conditions
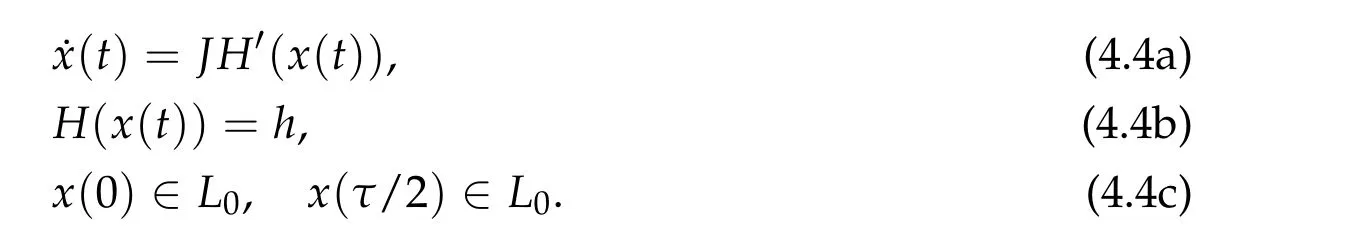
It is clear that a solution (τ,x) of (4.4a)-(4.4c) is a characteristic chord on the contact submanifold Σ :=H−1(h)={y ∈R2n|H(y)=h}of(R2n,ω0)and satisfies

In general, this kind ofτ-periodic characteristic (τ,x) is called a brake orbit on the hypersurface Σ. We note that the problem(4.2a)-(4.2b)with the Hamiltonian functionHdefined in(4.1)is a special case of the problem(4.4a)-(4.4c).We denote byJb(Σ,H)the set of all brake orbits on Σ. Two brake orbits(τi,xi)∈Jb(Σ,H)withi= 1,2,are equivalent,if the two brake orbits are geometrically the same,i.e.,x1(R)=x2(R).We denote by[(τ,x)]the equivalence class of(τ,x)∈Jb(Σ,H) in this equivalence relation and by ˜Jb(Σ,H)the set of [(τ,x)] for all (τ,x)∈Jb(Σ,H). In fact ˜Jb(Σ,H) is the set of geometrically distinct brake orbits on Σ,which is independent of the choice ofH. So from now on we simply denote it by ˜Jb(Σ)and in the notation[(τ,x)]we always mean thatxhas the minimal periodτ. We also denote by ˜J(Σ)the set of all geometrically distinct closed characteristics on Σ. The number of elements in a setSis denoted by#S. It is well known that# ˜Jb(Σ)(and also#˜J(Σ))depends only on Σ,that is to say,for simplicity we takeh= 1,ifHandGare twoC2functions satisfying (4.3) and ΣH:=H−1(1) = ΣG:=G−1(1),then#Jb(ΣH) =#Jb(ΣG). So we can consider the brake orbit problem in a more general setting. Let Σ be aC2compact hypersurface inR2nbounding a compact setCwith nonempty interior. Suppose Σ has non-vanishing Gaussian curvature and satisfies the reversible conditionN(Σ−x0) = Σ−x0:={x −x0|x ∈Σ}for somex0∈C. Without loss of generality, we may assumex0= 0. We denote the set of all such hypersurfaces inR2nbyHb(2n). Forx ∈Σ, letnΣ(x) be the outward unit normal vector atx ∈Σ as in (3.3). Note that here by the reversible condition there holdsnΣ(Nx) =NnΣ(x). We consider the dynamics problem of findingτ> 0 and aC1smooth curvex: [0,τ]→R2nsuch that
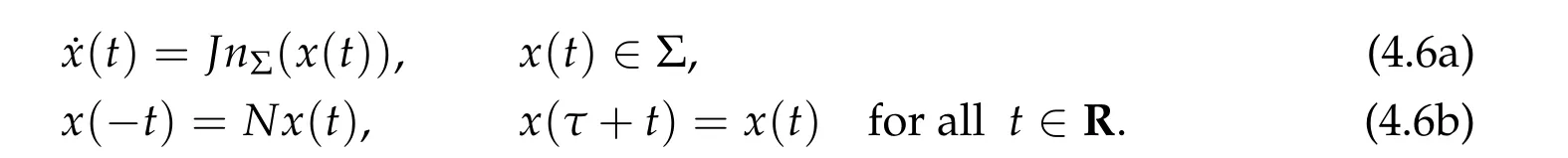
A solution (τ,x) of the problem (4.6a)-(4.6b) determines a brake orbit on Σ. Now the generalized Seifert conjecture can be represented as
The Generalized Seifert Conjecture:For any Σ∈Hb(2n),there holds
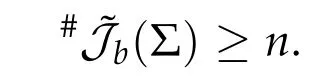
We can view the above estimate as a result on the number of Lagrangian intersection(more precisely the Legendre intersection,since Σ∩L0is a Legendre submanifold of the contact manifold Σ)of“reversible”Hamiltonian mapϕb:

The famous Arnold conjecture is related to the Lagrangian boundary problem, it says that the number of Lagrangian intersection of a Hamiltonian map on a closed symplectic manifoldMcan be estimated from below by the Betti number ofMin the non-degenerate case and by the cuplength ofM[4]of 1965. In this direction readers are referred to[22,34,39]of 1989,1998,and 2005 respectively.
4.3 Some related results since 1948
As a special case, lettingA(q) =Iin (4.1), the problem (4.2a)-(4.2b) corresponds to the following classical fixed energy problem of the second order autonomous Hamiltonian system
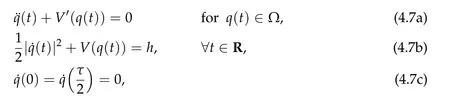
whereV ∈C2(Rn,R)andhis a constant such that Ω≡{q ∈Rn|V(q) A solution(τ,q) of(4.7a)-(4.7c)is still called a brake orbit in ¯Ω. Two brake orbitsq1andq2:R→Rnare geometrically distinct ifq1(R)/=q2(R). We denote byO(Ω,V)and ˜O(Ω)the sets of all brake orbits and geometrically distinct brake orbits in ¯Ω respectively. Remark 4.1.It is well known that via x=(p,q)andp= ˙q,the elements inO(Ω,V)and the solutions of(4.4a)-(4.4c)are one to one correspondent. After 1948,various studies have been carried out for the brake orbit problem. Bolotin proved in [8] of 1978 the existence of brake orbits in general setting. Hayashi in [31] of 1983, Gluck and Ziller in [28] of 1983, and Benci in [6] of 1984 proved#˜O(Ω)≥1, ifVisC1, ¯Ω ={V ≤h}is compact, andV′(q)/= 0 for allq ∈∂Ω. Rabinowitz in [62] of 1978 proved that ifHsatisfies(4.3),Σ≡H−1(h)is star-shaped,andx·H′(x)/= 0 for allx ∈Σ, then#˜Jb(Σ)≥1. Benci and Giannoni gave a different proof of the existence of one brake orbit in [7] of 1989. In 2005, it was pointed out in [24] of Giamb`o, Giannoni and Piccione that the problem of finding brake orbits is equivalent to find orthogonal geodesic chords on manifold with concave boundary. Giamb`o, Giannoni and Piccione in [25] of 2010 proved the existence of an orthogonal geodesic chord on a Riemannian manifold homeomorphic to a closed disk and with concave boundary. For the multiplicity of the brake orbit problems, Weinstein in [69] of 1973 proved a local result: AssumeHsatisfies(4.3). For anyhsufficiently close toH(z0)withz0being a nondegenerate local minimum ofH,there exist at leastngeometrically distinct brake orbits on the energy surfaceH−1(h). In[9]of 1978 of Bolotin and Kozlov and in[28]of 1983 of Gluck and Ziller,the existence of at leastnbrake orbits was proved under assumptions of Seifert in [64]and an additional assumption on the energy integral such that different minimax critical levels correspond to geometrically distinct brake orbits. Szulkin in [65] of 1989 proved that#˜Jb(H−1(h))≥n,ifHsatisfies conditions in[62]of 1978 of Rabinowitz and the energy hypersurfaceH−1(h)is 2-pinched. Groesen in[29]of 1985 and Ambrosetti,Benci and Long in[1]of 1993 also proved#˜O(Ω)≥nunder different pinching conditions. Definition 4.1.We denote by Without any pinching conditions,Long,Zhang and Zhu in[57]of 2006 established a Maslov-type index theory for brake orbits and proved In order to show the role of iteration theory ofiLindex,we give a sketch of the proof of Theorem 4.2 below by applying Theorem 3.4 and the estimate in Theorem 2.3. More details can be found in[48]. For anyxτbeing aτ-periodic brake orbit solution, letγxτbe the symplectic path associated toxτ. We define we obtain a sufficient large integerRand the iteration timesm1,m2,···,mp+q,mp+q,mp+q+1,···,mp+2qsatisfying(i)-(vi)of Theorem 3.4. By the proofs in [57] of Long, Zhang and Zhu in 2006 and the fact thatxand−xhave the sameiL0andνL0index,we can define a mapφwith such that 1≤k(s)≤p+qand Step 2Let We shall prove that In fact,by the strict convexity of Σ,we haveiL0(xk(s))≥0. Hence by(4.8a)and(iii)of Theorem 3.4,for everys=1,2,···,n,there holds (4.11)and(ii)of Theorem 3.4 would yield Note that the convex assumption of the hypersurface Σ implies that theiL0(x,j)andiL0(x,j)+νL0(x,j) are both strictly increasing in the iteration timejfor any brake orbitxon Σ. Hence by(4.10),(4.12),we obtain Hence(4.9)holds. Step 3(4.8b)and(4.9)imply#S1≤p. By similar arguments,we obtain which yields#S2≤2q. So we have The proof of Theorem 4.2 is completed. Remark 4.2.Theorem 4.2 is a kind of multiplicity result related to the Arnold chord conjecture. The Arnold chord conjecture is an existence result which was proved by Mohnke in[60]of 2001. Another kind of multiplicity result related to the Arnold chord conjecture was proved by Guo and Liu in[30]of 2008. Ifrj/rk ∈RQwheneverj/=k,one can easily see that there are preciselyngeometrically distinct symmetric brake orbits onEn(r)and all of them are nondegenerate. The following two important results are direct consequences of Theorem 4.2. Corollary 4.1([48]).If H(p,q)defined by(4.1)is even and convex,then Seifert conjecture holds.Corollary 4.2([48]).Suppose V(0) = 0, V(q)≥0, V(−q) =V(q)and V′′(q)is positive definite for all q ∈Rn{0}. Then for any given h> 0andΩ≡{q ∈Rn|V(q) In 2015,by non-smooth Lyusternik-Schnirelmann theory,Giamb`o,Giannoni and Piccione proved the following result which means Seifert conjecture holds in the casen=2 while it is still open forn ≥3. Theorem 4.3([26]).Under Seifert’s condition with A and V weakened to C2, for n ≥2, there holds We call a compact star-shaped reversible hypersurface Σ∈R2nbeing dynamically convex,if for any brake orbit(τ,x)on Σ,there holds We call Σ isL0-nondegenerate if every brake orbits on it is nondegenerate. In a preprint of 2018,using the equivariant wrapped Floer homology theory and the Common Index Jump Theorem 3.4,Kim,Kim and Kwon proved, Theorem 4.4([38]).For any L0-nondegenerate compact dynamically convex reversible hypersurfaceΣ∈R2n,there holds The conclusion of Theorem 4.2 can be extended to dynamically convex case. Theorem 4.5([49] of Z. Liu and Zhang).For any compact symmetric dynamically convex reversible hypersurfaceΣ∈R2n,there holdsIn 2006,Zhang considered the multiplicity of symmetric brake orbits and proved, For stability of brake orbits, there are only few results, since information obtained from variational methods is not easy to be used. In 2017,Fan and Zhang proved, Then all of the n closed characteristics onΣare symmetric brake orbits after suitable time translation. Note that for the hypersurface we have where we have denoted by ˜Jsb(Σ) the set of all symmetric brake orbits on Σ. We also note that on the hypersurface Σ ={x ∈R2n||x| = 1}there are some non-brake closed characteristics. Forn= 2,it was proved in[33]of Hofer,Wysocki and Zehnder that#˜J(Σ)is either 2 or+∞for anyC2compact convex hypersurface Σ inR4. In the brake orbit case,in[23]of 2016, Frauenfelder and Kang proved that#˜Jb(Σ) is either 2 or +∞for anyC2compact dynamically convex reversible hypersurface Σ inR4. So it is natural to propose the following conjecture: Conjeture:#˜Jb(Σ)is eithernor+∞for anyC2compact convex reversible hypersurface Σ inR2n. The multiplicity of closed characteristics on a fixed energy hypersurface inR2nis a very important problem in nonlinear Hamiltonian systems. Similar to Seifert conjecture,there is a long standing(more than 100 years)conjecture that on every compact convex hypersurface inR2n, there exist at leastnclosed characteristics. An important progress was made by Long and Zhu in [59] of 2002, by using the iteration theory of Maslovtype index of symplectic paths and establishing the common index jump theorem. They proved that Then in 2002,Liu,Long and Zhu in[45]proved that provided Σ is a convex compact symmetric hypersurface inR2n. It is also interesting to ask the following question:Can we prove the above conjecture on closed characteristics if the hypersurface is additionally reversible? For the nonlinear Hamiltonian system: in his pioneering paper[61]of 1978,Rabinowitz proved the following famous result via a variational method. SupposeHsatisfies the following conditions: (H1′)H ∈C1(R2n,R). (H2)There exist constantsµ>2 andr0>0 such that (H3)H(x)=o(|x|2)atx=0. (H4)H(x)≥0 for allx ∈R2n. Then for anyT>0,the system(5.1)possesses a non-constantT-periodic solution. Because aT/kperiodic function is also aT-periodic function,in[61]Rabinowitz proposed the conjecture that under conditions (H1′) and (H2)-(H4), there is a periodic solution of (5.1) withTas its minimal period for anyT> 0. Since 1978, this conjecture has been deeply studied by many mathematicians. A significant progress was made by Ekeland and Hofer in their celebrated paper [18] of 1985, where they confirmed Rabinowitz’s conjecture for the strictly convex Hamiltonian systems. For Hamiltonian systems with convex or weakly convex assumptions,we refer to[2,3,12,17,44,56]and references therein for more details. For the seconder order case without any convex condition we refer to[50–52], and Chapter 13 of[56]as well as references therein. In[12]of 1997,Dong and Long gave the first index theoretical proof of the Ekeland-Hofer theorem,and discovered the deep connection between the minimal period and the index theory. It is natural to consider the minimal period solution problem of brake orbits in reversible first order nonlinear Hamiltonian systems. The key tool is the iteration theory ofiLindex. Motivated by [12,20,21,50,51] we consider the case that the systems are semipositive,i.e.,the HessianH′′(x)has no negative eigenvalues at anyx ∈R2n,which guarantees the existence of a lower bound ofiLindices of brake orbits of the system. It is natural to supposeHsatisfies the following reversible and semipositive conditions: (H5)H(Nx)=H(x)for allx ∈R2n. (H6)H′′(x)is semipositive definite for allx ∈R2n. We also suppose the following smooth condition: (H1)H ∈C2(R2n,R). In order to introduce our results more conveniently, we define the following (B1)condition. Since the Hamiltonian systems considered here are reversible, this condition is natural. (B1)Condition. For anyτ>0 andB ∈C([0,τ],Ls(R2n)of then×nmatrix square block form satisfyingB12(0) =B21(0) = 0 =B12(τ) =B21(τ), we callBsatisfying the condition (B1). For anyB ∈C([0,τ],Ls(R2n)),denote byγBthe fundamental solution of the following problem For readers’ convenience we give the idea of Theorem 5.2 below as an example to show how to estimate the minimal period by the index iteration theory,more details can be found in[72]of Zhang in 2015. Idea of the proof of Theorem5.2.For anyτ> 0, by the Galerkin approximation and the variational argument, we obtain aτ-periodic brake orbit solutionxτof (5.1) such thatiL0(xτ)≤1. Suppose its minimal period isT,thenτ/T ≡kis a positive integer andxτ=xkTwithxT=xτ|[0,T]. In the variational argument we also haveiL1(xT)+νL1(xT)≥1. By the semipositive assumption we have andiL0(γxT)+νL0(γxT)≥0 which implies Next we consider the minimal period problem for whereB0∈Ls(R2n). Theorem 5.3([72]).Let B0= diag(B11,B22)be a2n×2n real semipositive matrix with B11and B22being n×n matrices. Assume Remark 5.1.In[72],it was proved that ifB0is semipositive,theniL0(B0)+νL0(B0)≥0.Theorem 5.4([72]).Suppose that H satisfies the conditions(H1)-(H6)and (H7)H(−x)=H(x)for all x ∈R2n. Then for any τ> 0, the system(5.1)possesses a symmetric brake orbit with minimal period belonging to{τ,τ/3}. Acknowledgements The first author is partially supported by the NSFC Grants (No. 11790271), Guangdong Basic and Applied basic Research Foundation (No. 2020A1515011019), Innovation and Development Project of Guangzhou University. The second author is partially supported by National Key R&D Program of China(No.2020YFA0713300),NSFC Grants Nos. 11671215 and 11790271, LPMC of Ministry of Education of China, Nankai University, Nankai Zhide Foundation, Wenzhong Foundation, and the Beijing Center for Mathematics and Information Interdisciplinary Sciences at Capital Normal University. The third author is partially supported by National Key R&D Program of China(No.2020YFA0713300),NSFC Garnts Nos.11790271 and 11171341,and LPMC of Nankai University.
4.4 Recent progress on the Seifert conjecture
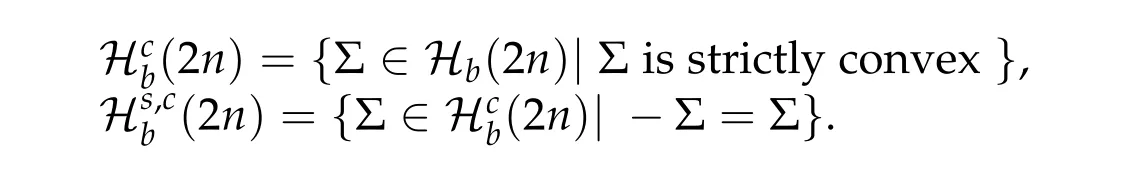
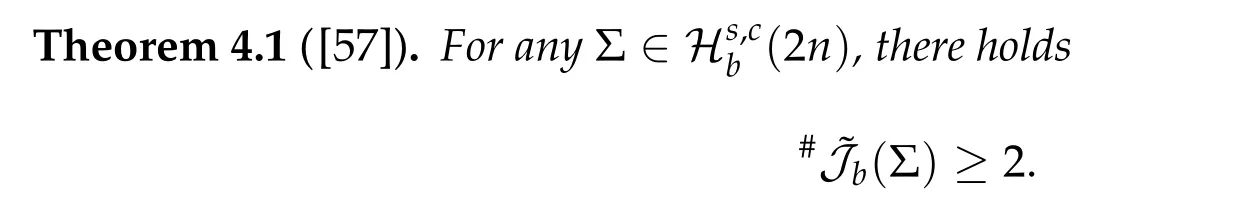


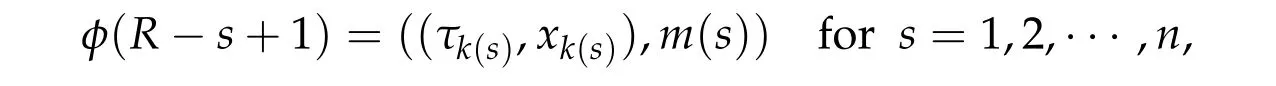
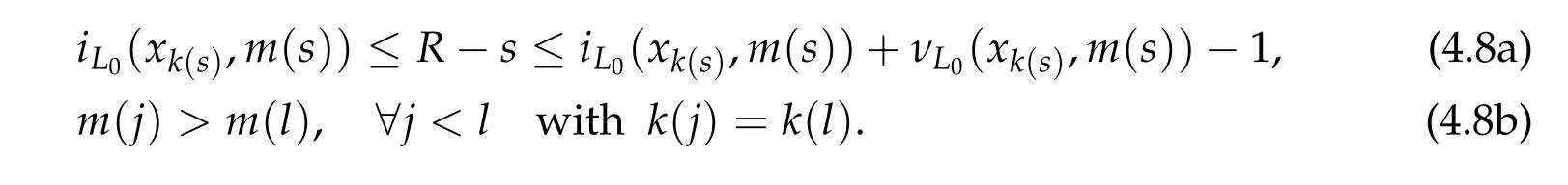


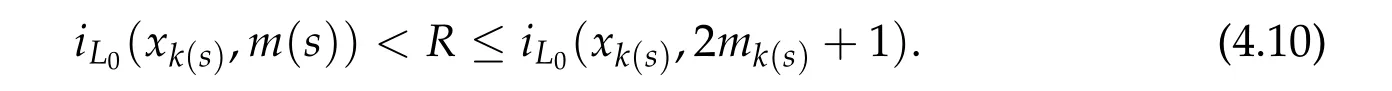

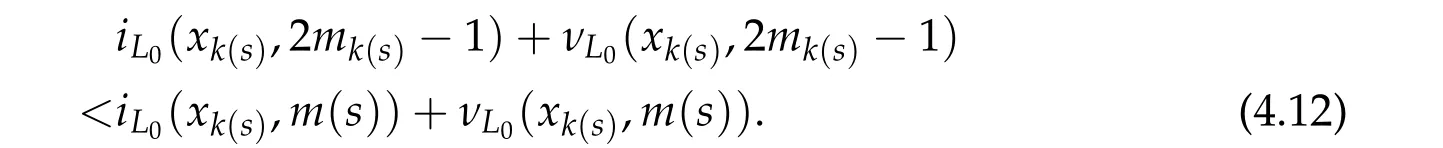
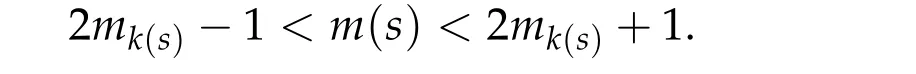
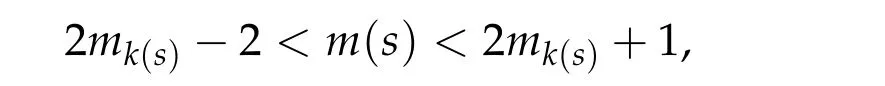
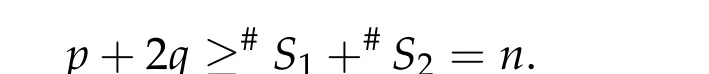



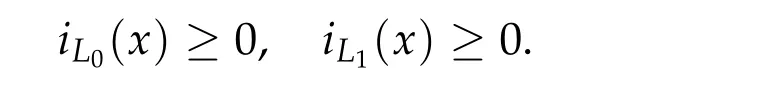
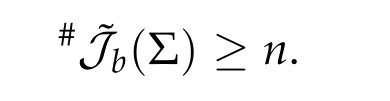
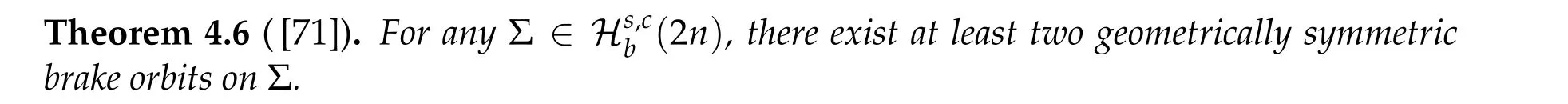
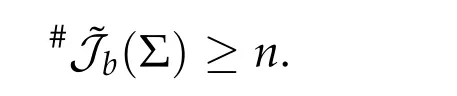
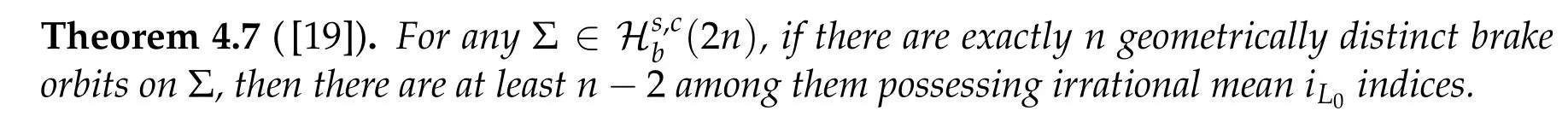
4.5 Related results
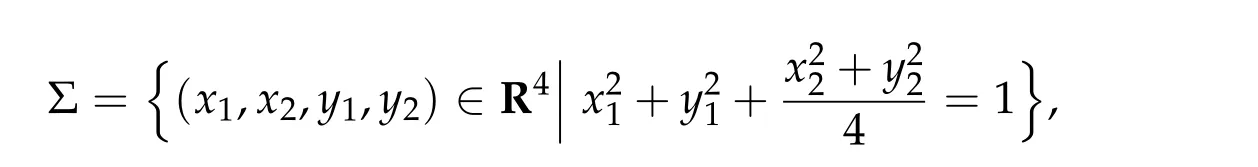

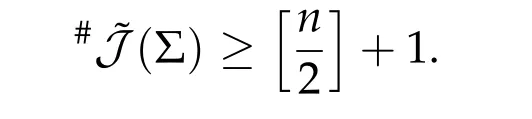
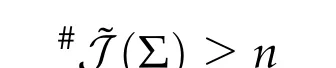

5 Applications,minimal period solution problems in the brake orbit case

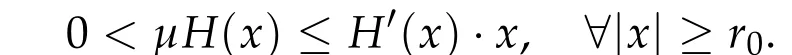

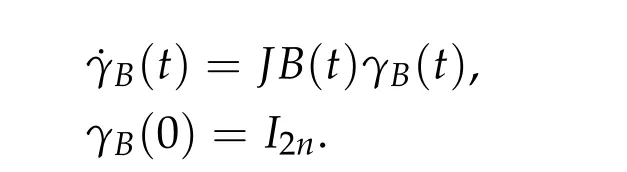





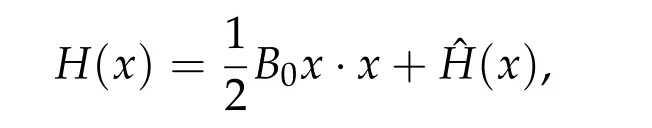
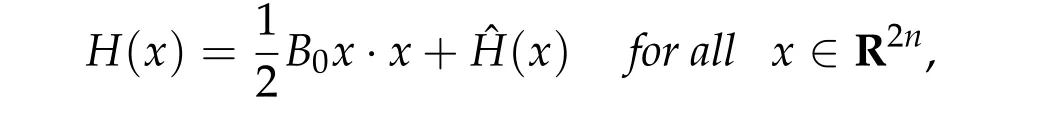
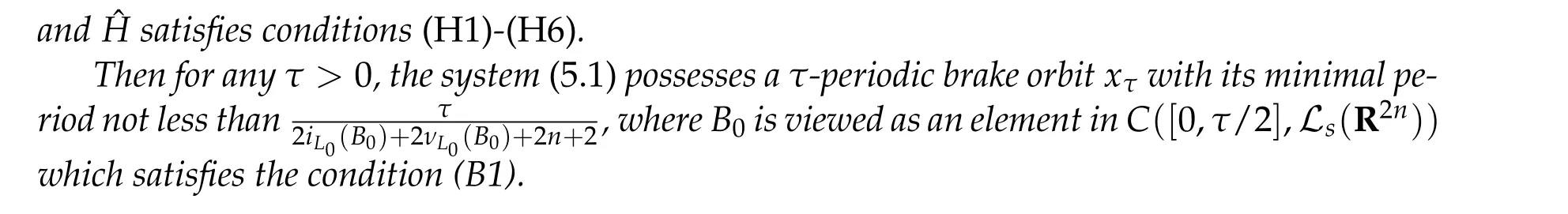

杂志排行
Analysis in Theory and Applications的其它文章
- Classification of Positive Ground State Solutions with Different Morse Indices for Nonlinear N-Coupled Schr¨odinger System
- Ground States to the Generalized Nonlinear Schrdinger Equations with Bernstein Symbols
- Diffusion with a Discontinuous Potential: a Non-Linear Semigroup Approach
- Deformation Argument under PSP Condition and Applications
- Multiple Sign-Changing Solutions for Quasilinear Equations of Bounded Quasilinearity
- Ground States to the Generalized Nonlinear Schr¨odinger Equations with Bernstein Symbols
