Classification of Positive Ground State Solutions with Different Morse Indices for Nonlinear N-Coupled Schr¨odinger System
2021-06-29JunchengWeiandMaodingZhen
Juncheng Weiand Maoding Zhen
1 Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2,Canada
2 School of Mathematics,Hefei University of Technology,Hefei,Anhui 230009,China
Abstract. In this paper,we study the following N-coupled nonlinear Schr¨odinger system
Key Words: Nonlinear Schr¨odinger system, unique ground state solution, variational method,Morse indices.
1 Introduction
In this paper,we study the followingN-coupled nonlinear Schr¨odinger system

wheren ≤3,N ≥3,µj> 0 are constants andβi,j=βj,i> 0 are coupling parameters(βj,j=µj). This paper is concerned with the uniqueness of ground state solution in the general caseN ≥3.
This system arises as standing wave solutions of the time-dependentN-coupled Schr¨odinger systems of the form

and these systems are also known as coupled Gross-Pitaevskii equations. In the past fifteen years,a great attention has been focused on the study of two coupled systems with nonlinear terms, both for their interesting theoretical structure and their concrete applications, such as in nonlinear optics and in Bose-Einstein condensates for multi-species condensates. By using variational methods or Lyapunov-Schmidt reduction methods,there are lots of results about existence, multiplicity and qualitative properties of nontrivial solutions of two coupled elliptic system. Since it seems almost impossible for us to provided a complete list of references,we refer the readers only to[1–11,18–20,25–27]and reference therein.

ForN-coupled system with mixed couplings,J.Wei and T.Lin[16]established some general theorems for the existence and nonexistence of ground state solution and showed that when allβi,jare positive and the matrix B is positively definite,there exist a ground state solution which is radially symmetric. However, if allβi,jare negative, or one ofβi,jis negative and the matrix B is positively definite, there is no ground state solution.Recently, J. Wei and Y. Wu [28] gave a systematic and an (almost) complete study on the existence of ground state solution for N-coupled system when the system admits mixed couplings. By dividing this system into repulsive-mixed and total-mixed cases,they proved the nonexistence of ground state solution for repulsive-mixed case and gave an necessary condition for the existence of ground state solution for total-mixed cases.Peng et al.[21]use a construction argument for singularly perturbed elliptic problems to obtain vector solutions with some of the components synchronized between them while being segregated with the rest of the components simultaneously.
Inspired by the above-mentioned works, especially by [14,22,28], in this paper our goal is two-folds. One is to give a complete classification of ground state solution with different Morse indices for three-coupled Schr¨odinger system under suitable conditions.Another goal of the paper is to give a different approach from [14] to get the existence of ground state solutions for N-coupled system. The difficulty is that we can’t use the method introduced in [14], where the authors considered the ground state solution with Morse indexNon bounded domain of Rn, when the parameter satisfies−λ1(Ω)<λ1=···λN=λ< 0. The novelty is that in order to obtain the unique minimum point ofg(τ1,···,τN),(2.6b),it is not feasible to use the method in[22]by directly calculate the second derivative to determine the unique minimum values, so we use the method of Lagrange’s multiplier, implicit function theorem and the Cramer’s Rule to show there exists a unique(τ1,min,···,τN,min),τi,min> 0,i= 1,···,N,such thatg(τ1,min,···,τN,min) =g(t1,···,tN)min(see details in Lemma 3.3). Then we give a complete classification of ground state solutions with Morse index 1 for system (1.1) under suitable conditions. We prove that all the ground state solutions of(1.1)must be the form of(c1w,···,cNw),wherewis the unique positive ground state solution of(1.5). Finally,we generalize our results to fractionalN-coupled Schr¨odinger system.
Before we state our main results we introduce some notations. LetH1(Rn) be the Hilbert space of functions in Rnendowed with the standard scalar product and norm
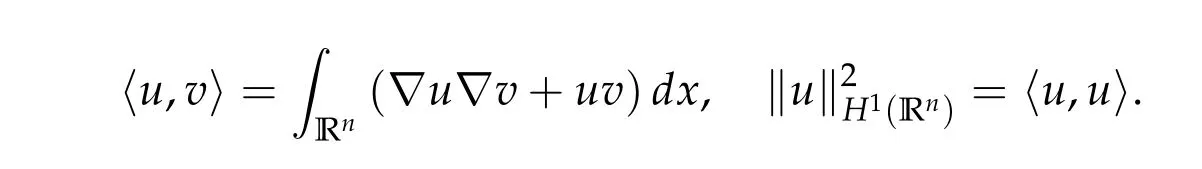
The energy functional associated with(1.1)is given by
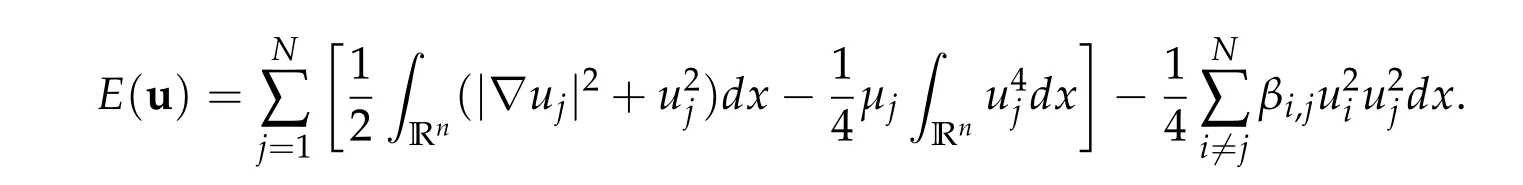
Define two Nehari manifolds
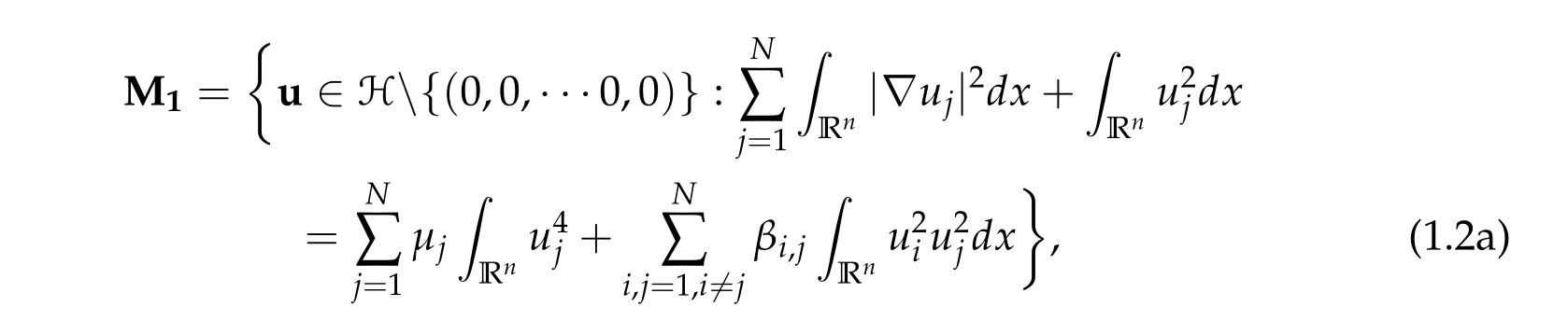

foru=(u1,···,uN)∈H and H=(H1(Rn))N.
We say thatuis a ground state solution of(1.1),ifuj> 0,j= 1,···,N,usolves(1.1)andE(u)=ai,i=1,N. Ifuis a nontrivial solution of(1.1),thenuis inMl,l=1,N. It is easy to see thatMl/= ∅. In fact,if we takeϕj ∈C∞c(Rn),j=1,···,N,withϕj/≡0 and
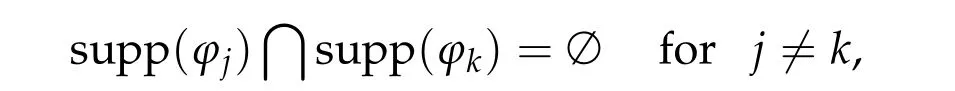
then there existst1,···,tN>0,such that(t1ϕ1,···,tNϕN)∈Ml.
To state our results,we introduce the matrix B and B−as following,where B−is the inverse matrix of B
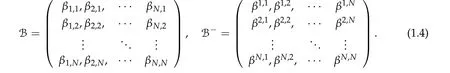
From[15],we can letwbe the unique positive solution of following problem
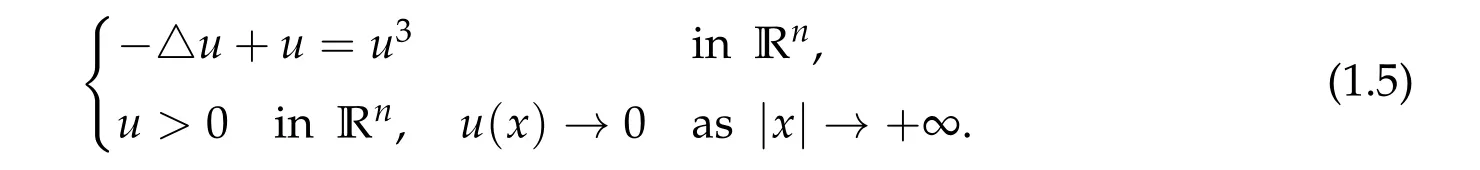
By Lemma 1 and Lemma 2 in[16],wis also the unique positive ground solution of above problem.
2 Statement of main results
Before we present the results in the general caseN ≥3,we first explain the key ideas and main results whenN=3.
We first study the following three-coupled nonlinear Schr¨odinger system

wheren ≤3,µj> 0 are constants andβi,j=βj,i> 0,i,j= 1,2,3. By the method of moving plane,we can assume that all solutions to(2.1)are radially symmetric.
We first give an almost complete classification of ground state solution with different Morse indices for 3-coupled system under suitable conditions. We will show that any positive ground state solution with different Morse indices must be the form of(c1w,c2w,c3w), wherewis the unique positive ground state solution of (1.5). As far as we know, there are some results about the existence and nonexistence of ground state solution. J. Wei and Y. Wu [28] gave an (almost) complete study on the existence and nonexistence of ground state solution with different Morse indices of (2.1) under different conditions by the idea of block decomposition and measure the total interaction between different blocks for 3-coupled system when the system admits mixed couplings.For other results about the existence and nonexistence of ground state solution for threecoupled system,see[16,17,23]and references therein.
We state our main results now. By the the definition of Morse index,it is well-known that if the ground state solution of (2.1) is defined on Nehari manifoldM1(see(1.2a)),then the ground state solution has Morse index 1. If the ground state solution of (2.1)is defined on Nehari manifoldM3(see(1.2b)),then the ground state solution has Morse index≤3. If the ground state solution of(2.1)is defined on Nehari manifoldM2defined below
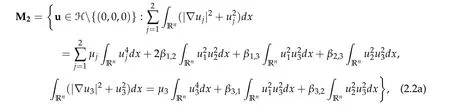


which implies that the Morse index ofvis greater than or equals to 3. Thus,vis a ground state with Morse index 3. The other cases is similar as the proof of Morse index 3,so we omit the details here.
For ground state solution with Morse index 1,we define a multivariate function

We first prove that iff(τ1,τ2,τ3) has a unique positive minimum point(τ1,min,τ2,min,τ3,min) under suitable conditions, then we show that (ηminτ1,minw,ηminτ2,minw,ηminτ3,minw)is the unique positive ground state solution of(2.1)(whereηminis some positive constant defined later). For ground state solution with Morse index 3,the key step is to show(d1w,d2w,d3w) is a ground state solution of(2.1)when matrix B and B−(see(1.4))satisfy suitable conditions,wheredi,i=1,2,3 satisfy

Then by the same arguments as above step, we can show that if (u1,0,u2,0,u3,0) be any positive ground state solution of(2.1),then(u1,0,u2,0,u3,0)=(d1w,d2w,d3w).
For ground state solution with Morse index 2, we first prove (d1w,md1w,d3w) is a ground state solution of(2.1),whered1,d3satisfy following equation,

Then we prove that if (u12,0,mu12,0,u3,0) be any positive ground state solution of (2.1)with Morse index 2 on Nehari manifoldM2,then(u12,0,mu12,0,u3,0)=(d1w,md1w,d3w).
Let the matrix B and B−be defined at(1.4)andf(τ1,τ2,τ3) be defined at(2.3). Our first result on three-component system is the following on classification of ground state solutions with Morse index 1.
Theorem 2.1.Assume βi,j ≥0,if(τ1,0,τ2,0,τ3,0)satisfies ∇f(τ1,τ2,τ3) =0,then(η0τ1,0w,η0τ2,0w,η0τ3,0w)is a positive solution of(2.1),where
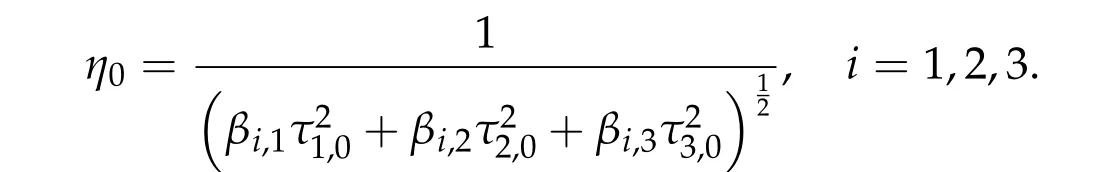
Conversely,under the condition that β∗j< 2,for all j= 1,2,3and thatdet B/= 0, f has a unique global minimum(τ1,min,τ2,min,τ3,min),τi,min>0,i=1,2,3,and

is the unique positive ground state solution of(2.1)with the Morse index 1,where
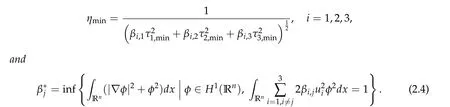
Here, uj are the ground state state solution of two-coupled system. If j= 3, then(u1,u2)is a ground state solution of system(2.1)when u3=0. The other cases are similar.
Furthermore all ground state solutions to(2.1)must be
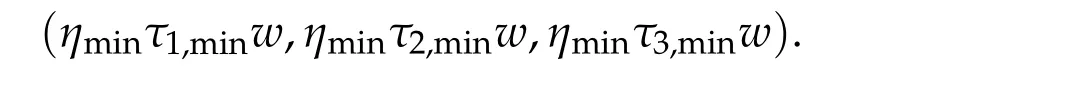
The next theorem classifies ground state solutions with Morse index 3.
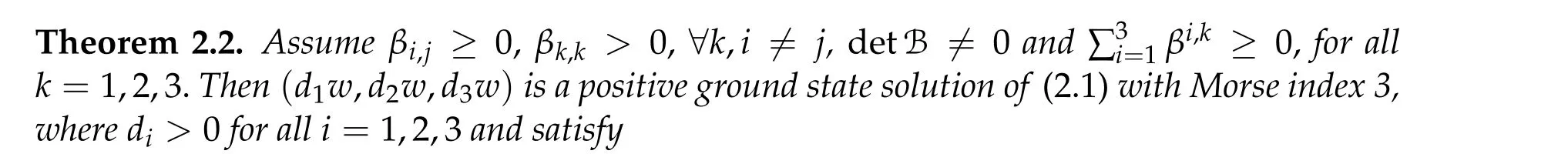
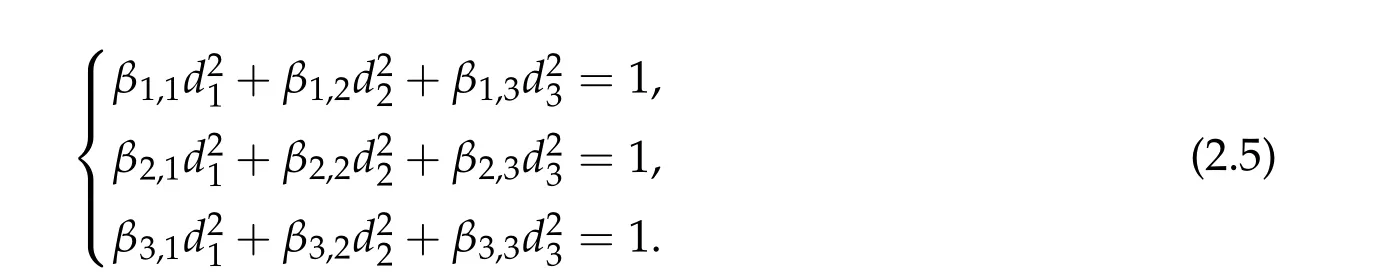
Conversely,(d1w,d2w,d3w)is the unique positive ground state solution of(2.1)with Morse index 3.
The last result on three-component system classifies the ground state solutions with Morse index 2.
Theorem 2.3.Assume βi,j ≥0,βk,k> 0,∀k,i/=j,det D/= 0,D−is an inverse matrix ofDand(1+m2)D11+D21≥0, (1+m2)D12+D22≥0.If(u12,0,mu12,0,u3,0)be any positive ground state solution of(2.1)with Morse index 2 on Nehari manifoldM2, then(u12,0,mu12,0,u3,0)=(d1w,md1w,d3w),where d1,d3satisfy following equation,
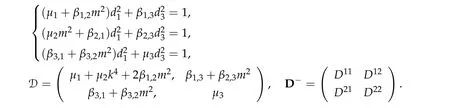
Theorem 2.1 can be extended toN-component system as follows.
Theorem 2.4.Assume βi,j ≥0,if(τ1,0,τ2,0,···,τN,0)satisfies ∇g(τ1,τ2,···,τN)=0,then

is a positive solution of(1.1),where

Conversely,under the condition that β∗j< 2,for all j= 1,···,N and thatdet B/= 0, g has a unique global minimum(τ1,min,τ2,min,···,τN,min),τi,min>0,i=1,···,N,and

is the unique positive ground state solution of(2.1)with the Morse index 1,where
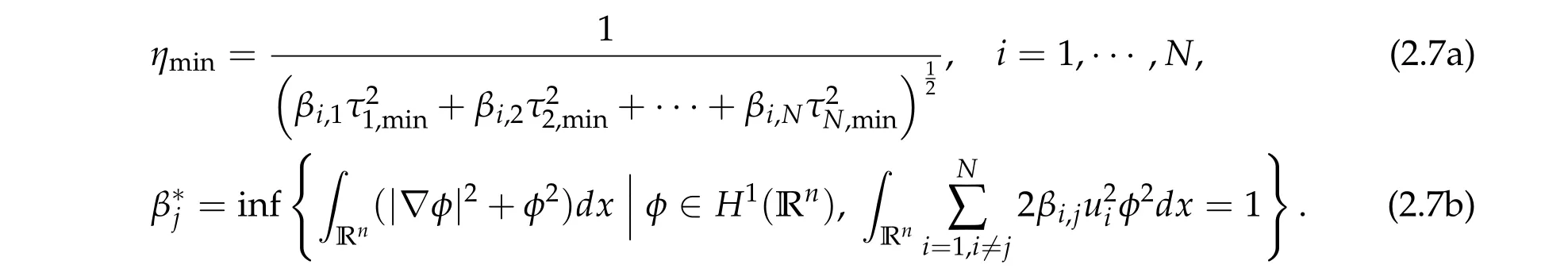
Furthermore,all ground state solutions to(2.1)must be
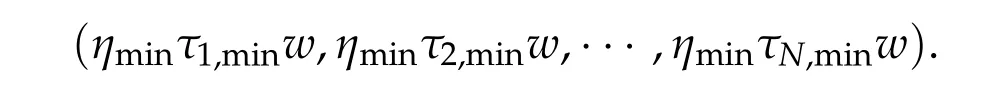
Similarly Theorem 2.2 can be extended toN−component systems:
Theorem 2.5.Assume βi,j ≥0,βk,k> 0,∀k,i/=j,det B/= 0and∑Ni=1βi,k ≥0,for all k= 1,···,N.Then(d1w,d2w,···,dNw)is a positive ground state solution of(1.1)with Morse index N,where di>0for all i=1,2···,N and satisfy
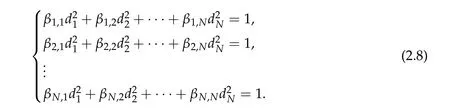
Conversely(d1w,d2w,···dNw)is the unique positive ground state solution of(1.1)with Morse index N.
Remark 2.1.The similar results as Theorem 2.5 can be found in Guo et al. in[14],where the authors considered the ground state solution with Morse index N for N-coupled system on bounded domain of Rn, when the parameter satisfy−λ1(Ω)<λ1=···λN=λ<0.
Remark 2.2.We should point out that Theorem 2.1 to Theorem 2.5 are also true for corresponding fractional Laplacian system,since for the following subcritical fractional equation

R. L. Frank and E. Lenzmann [12] showed the unique positive radial least energy solutions for one dimension case and R.L.Frank,E.Lenzmann and L.Silvestre[13]showed the general unique ground state solution for dimension greater than one.
Remark 2.3.In order to obtain the unique minimum point ofg(τ1,···,τN), (2.6b)it is not feasible to use the method in [22] by directly calculate the second derivative to determine the unique minimum values, so we use the method of Lagrange’s multiplier, implicit function theorem and the Cramer’s Rule to show there exists a unique (τ1,min,···,τN,min),τi,min> 0,i= 1,···,N, such thatg(τ1,min,···,τ1,min) =g(t1,···,tN)min(see details in Lemma 3.3).
The paper is organized as follows. In section 3,we introduce some preliminaries that will be used to prove theorems. In Section 4,we prove Theorem 2.1 and Theorem 2.4. In Section 5,we prove Theorem 2.2 and Theorem 2.5. Finally,Theorem 2.3 will be proved in Section 6.
3 Some preliminaries
The energy functional associated with(2.1)is given by
Recall the Nehari manifoldsM1,M2,M3as defined in(1.2a),(1.2b)and(2.2)respectively.Consider the minimization problems
Define
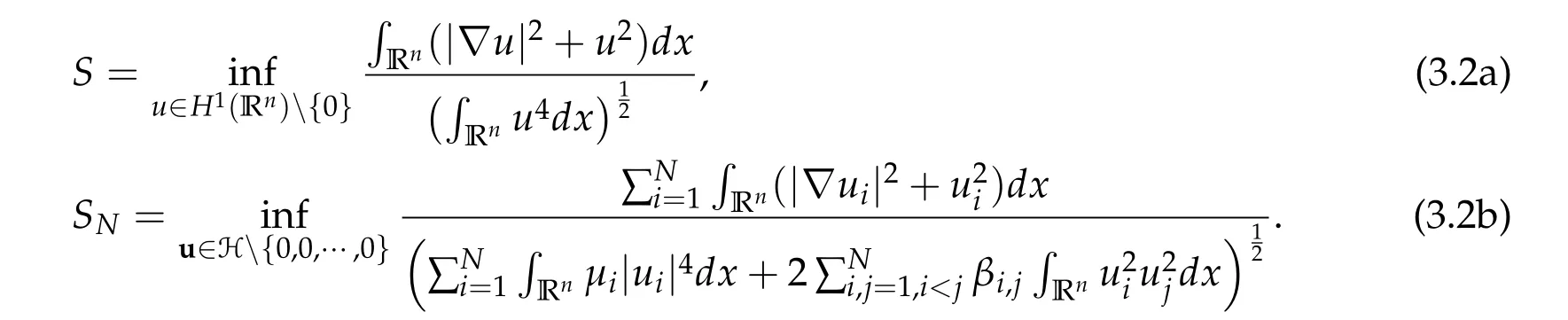
We first have the following lemma.
Lemma 3.1.For

where
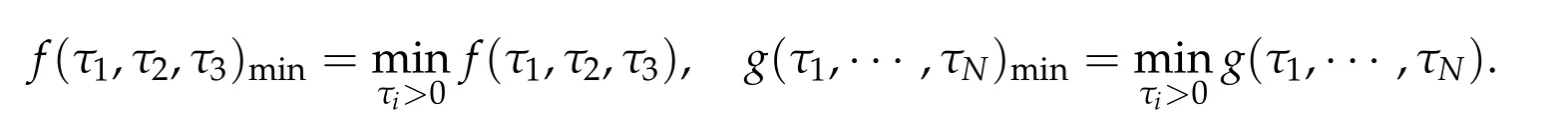
Proof.For anyϕ ∈H1(Rn){0},letf(τ1,min,τ2,min,τ3,min)=f(τ1,τ2,τ3)minand
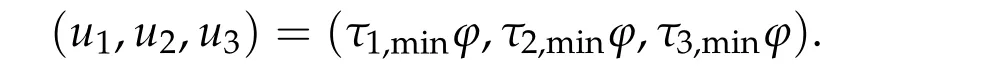
Then by the definition ofS3,we have
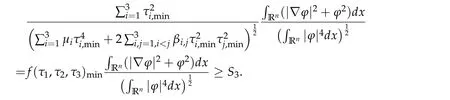
Hence

On the other hand, let (u1,n,u2,n,u3,n)∈H be a minimizing sequence ofS3. Letzi,n=ti,nui,n,i=1,2,3,where
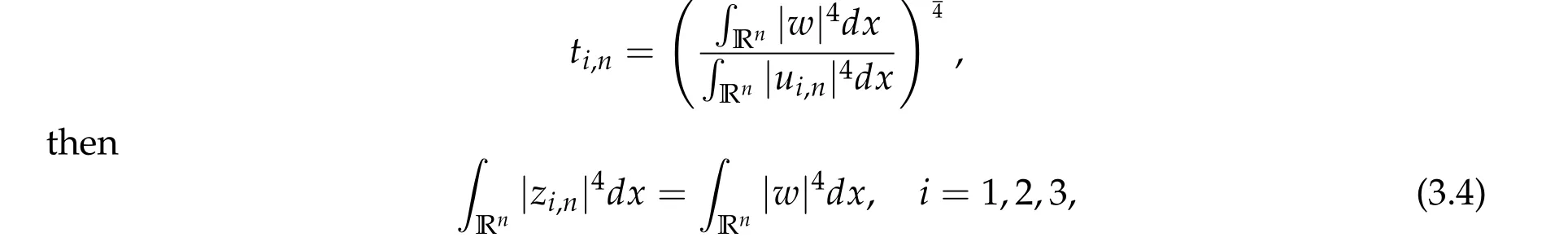
wherewis the unique positive solution of Eq. (1.5). By H¨older inequality and (3.4), we have
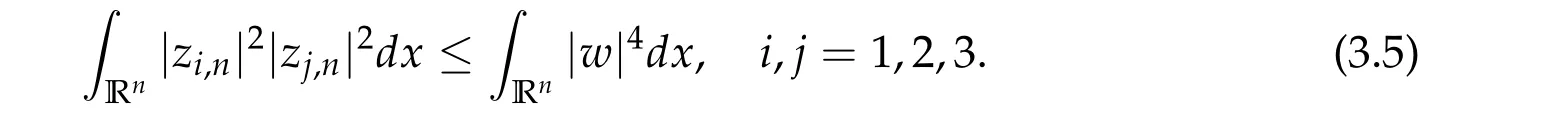
Therefore,by(3.5)andzi,n=ti,nui,n,i=1,2,3,we can deduce that

Letn →+∞. We have that

By(3.3)and(3.6),we get
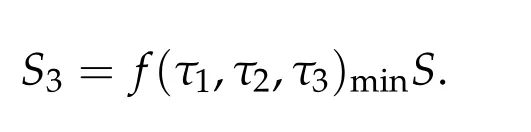
The case ofN ≥4 is similar.
T
o prove the existence and uniqueness of ground state solution,we study the properties off(τ1,τ2,τ3). To this end we first have following simple lemma
Lemma 3.2.If ∇f(τ1,τ2,τ3)=0,and

then(ητ1w,ητ2w,ητ3w)is a positive solution of(2.1).
Similarly,if ∇g(τ1,τ2,···,τN)=0,and
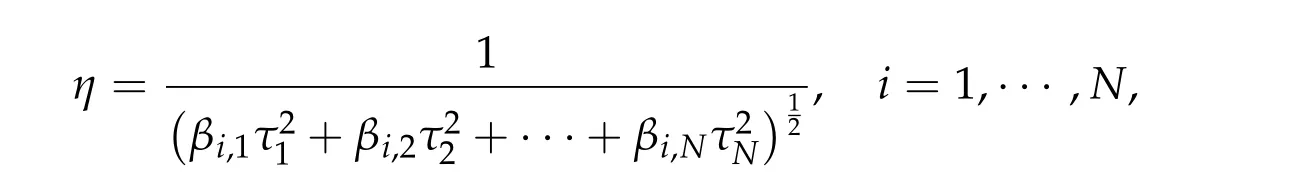
then(ητ1w,ητ2w,···,ητNw)is a positive solution of(1.1).
Proof.By direct calculation,we have
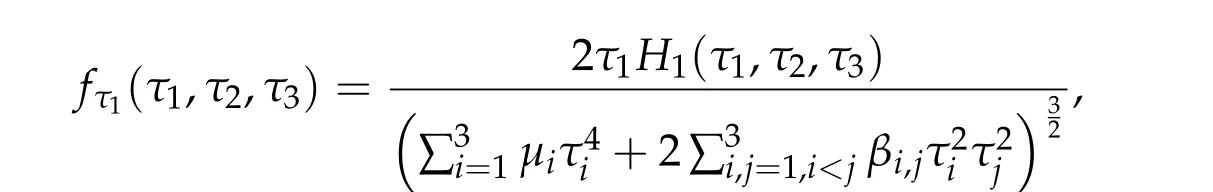
where

Similarly,we have

where
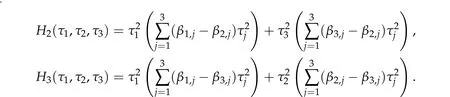
ThusHi(τ1,τ1,τ3)=0,i=1,2,3,which implies that
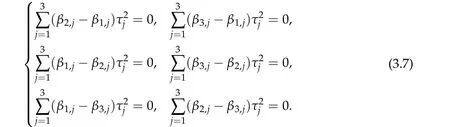
If(ητ1w,ητ2w,ητ3w)is a positive solution of(2.1),then

It is easy to see that(3.7)and(3.8)are equivalent.Hence,we complete the proof of Lemma 3.2. The proof in the case ofg(τ1,···,τN)is similar and thus omitted.

Then
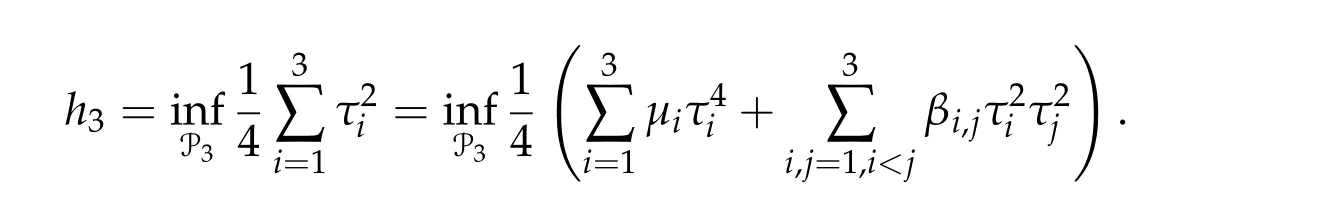
By a standard argument,we can see that
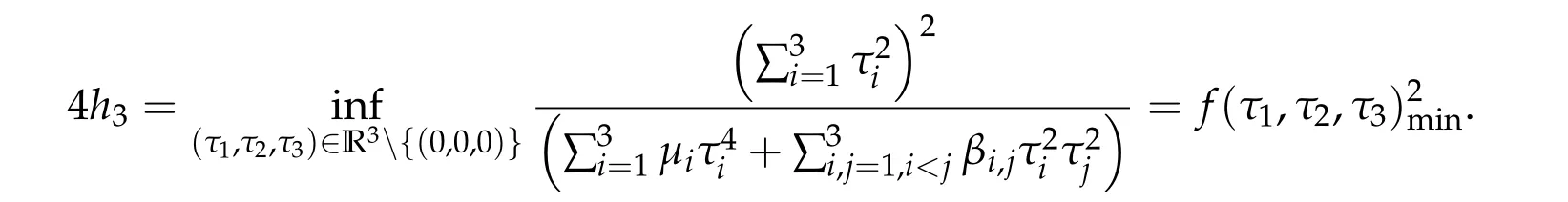
Thus,h3can be attained by someτi,min≥0 for alli= 1,2,3 andτi,min> 0 for somei. By the method of Lagrange’s multiplier,τi,min≥0 for alli= 1,2,3 also satisfies the following system

Next,we proveτi,min>0 for alli=1,2,3.
To show thatτ3,min> 0,we just need to prove thatc1 such that(t(s)u1,t(s)u2,t(s)sφ)∈M1fors>0 small enough. So, forβ∗3<2 ands>0 is small enough. Thus,we haveτ3,min>0. Similarly we can use the condition thatβ∗j<2, for allj=1,2,3 to show thatτi,min>0 for alli=1,2,3. Letsi=τ2i,min. Then(3.9)is equivalent to the following linear system By the Cramer’s Rule and the fact that det B/= 0, the linear system (3.10) has a unique solutions=(s1,s2,s3). The proof of second part of this lemma are similar to the first part of this lemma. To showτi,min> 0 for alli= 1,···,N,we letm= 1,···,N −1 andlm={l1,l2,···,lm} ⊂{1,···,N −1}withl1 where If we can show with then we can see thatτi,min> 0 for alli= 1,···,N. Without loss of generality, we assumecN−1=min{clm,m}and it is attained by(u1,u2,···,uN−1). By the implicit function theorem,there exists a unique such that(t(s)u1,t(s)u2,···,t(s)uN−1,t(s)sφ)∈M1fors>0 small enough. So, sinceβ∗i,N< 2 ands> 0 is small enough. Thus,we haveτN,min> 0. The other cases are similar. Proof of Theorem2.1and Theorem2.4.By Lemma 3.2, (η0τ1,0w,η0τ2,0w,η0τ3,0w) is a positive solution of(2.1),where and(τ1,0,τ2,0,τ3,0)satisfies∇f(τ1,τ2,τ3)=0. Next, we show that (ηminτ1,minw,ηminτ2,mimw,ηminτ3,minw) is the unique positive ground state solution of(2.1),where and(τ1,min,τ2,min,τ3,min)satisfies Since(ηminτ1,minw,ηminτ2,minw,ηminτ3,minw)is a positive solution of(2.1),we have Since∇f(τ1,min,τ2,min,τ3,min)=0,from(3.7)in Lemma 3.2,we have Thus,by(4.1)and direct calculation,we have So On the one hand, for any (u1,u2,u3)∈M1and by the definition ofS3(see (3.2b)), we have Hence On the other hand,by(4.2)and(ηminτ1,minw,ηminτ2,minw,ηminτ3,minw)∈M1,we have So, Consequently, (ηminτ1,minw,ηminτ2,minw,ηminτ3,minw) is a positive ground state solution of (2.1). If (τ1,min,τ2,min,τ3,min) is the unique minimum point off(τ1,τ2,τ3), then(ηminτ1,minw,ηminτ2,minw,ηminτ3,minw)is the unique positive ground state solution of(2.1)of the form(c1w,c2w,c3w). By Lemma 3.3 and above arguments, we complete the proof. The proof of Theorem 2.4 are similar to Theorem 2.1,we only need to replacei=3 toi=Nand use the second part of Lemma 3.2,we omit the details here. Next,we prove the second part of Theorem 2.1 and Theorem 2.4. Let (ηminτ1,minw,ηminτ2,minw,ηminτ3,minw) be the unique positive ground state solution of (2.1) of the form (c1w,c2w,c3w) and let (u1,0,u2,0,u3,0) be any positive ground state solution of(2.1)of Morse index 1. We first claim that To prove(4.3a)and(4.3b),we use implicit function theorem.We first consider the following 3-coupled system,whereµ1is replaced byµin system(2.1): and the following function where Thus(µ,τ1,τ2,τ3)=0,i=1,2,3,which implies that Since(τ1,min,τ2,min,τ3,min)is the minimum point off(τ1,τ2,τ3)(see(2.3)),we have By direct calculation,we have where By(4.6),we have Since(τi,min,τ2,min,τ3,min)is the minimum point off(τ1,τ2,τ3)(see(2.3)),then Let G=[Gi,j]3×3be the matrix defined above,then det G/=0 and so By the implicit function theorem,we know is alsoC1forµ ∈(µ1−∊,µ1+∊). Thus, the energy functional associated with (4.4) is given by Next,we show that Indeed,by the definition ofc1(µ),for any∊>0,we can take a(u1,u2,u3)/≡(0,0,0),such that Thus, On the other hand,by the definition of we can take a(u1,u2,u3)/≡(0,0,0)such that and(tuu1,tuu2,tuu3)satisfies(4.8),which implies that whereM1,µis a Nehari manifold whenµ1was replaced byµin Nehari manifoldM1.Thus So the proof of(4.7)is complete. Thus,there existst(µ)>0 such that wheret(µ)>0 satisfiesF(µ,t(µ))=0 and Since by implicit function theorem, there existsδ> 0 such thatt(µ1) = 1,t(µ1)∈C1(µ1−δ,µ1+δ)and By Taylor expansion,we have thus, Since then,by(4.9)-(4.11),we have Thus so Similarly, and Hence Since(ηminτ1,minw,ηminτ2,minw,ηminτ3,minw)is the ground state solution of(2.1),we have Thus, Thus,by(4.3a),(4.3b),we have Next,we prove Since(ηminτ1,minw,ηminτ2,minw,ηminτ3,minw)is a ground state solution of(2.1),we have Let then,by(4.12)and(4.13),we have Hence, Since(u1,0,u2,0,u3,0)and(ηminτ1,minw,ηminτ2,minw,ηminτ3,minw)are both the ground state solution of(2.1),we obtain which implies that So,ui,i=1,2,3 are positive ground state solutions of(1.5). Since(u1,0,u2,0,u3,0)satisfies(2.1)and we have So Since(1.5)has a unique positive ground state solutionw,thus,we have The proof is thus completed. The proof of second part of Theorem 2.4 is similar to the proof second part of Theorem 2.1. We choose auxiliary function as following So where The other part of the proof is similar as the proof of the second part of Theorem 2.1. Proof of Theorem2.2and Theorem2.5.We follow some ideas from [10] and recent work[29],where two-coupled system was considered. Indeed,by Lemma 1 and Lemma 2 in[16],wis the unique function attainingS.Thus, On the one hand,ifd1,d2,d3satisfy(2.5),it is easy to see that satisfies(2.1)and belongs toM3. So On the other hand,let(u1,n,u2,n,u3,n)∈M3be a minimizing sequence forc3,that is Define then by the definition ofS(see(3.2a))and H¨older inequality,we have Thus Similarly,we have Since we have Thus By(2.5),(5.2)to(5.4),we obtain We claim Indeed,from(5.5),we have where Next,we show Since B−is the invertible matrix of B,we let where By(5.5)and(5.6),we have Thus, So Combining(5.1)with(5.7),we have Thus, (d1w,d2w,d3w) is a positive ground state solution of (2.1). The proof of Theorem 2.5 are similar to above proof. To proof the uniqueness of positive ground state solution of (2.1), we show that if(u1,0,u2,0,u3,0)be any ground state solution of(2.1),then Let (u1,0,u2,0,u3,0) be any ground state solution of (2.1), then by strong maximum principle,we haveuj,0>0,j=1,2,3. We claim To proof the claim,we consider the following system,whereµ1is replaced byµin system(2.1). The corresponding energy functional is given by It is easy to see The next steps are same as the proof of Theorem 2.1 and Theorem 2.4. Thus, we have proof Thus,we complete the proof. So it is easy to see that(d1w,md1w,d3w)satisfies(2.1)and belongs toM2. So On the other hand,let(u12,n,mu12,n,u3,n)∈M2be a minimizing sequence forc2,that is Define then by the similar arguments as(5.2),we have Since So Thus,by(6.1),(6.3a),(6.3b)and(6.4),we have Next,we claim From(6.5),we have where Next,we show SinceD−is the invertible matrix of D,we let where If we let then So, Thus, So, Thus, So when (d1w,d2w,d3w)is a positive ground state solution of(2.1). Step 2. We show that if(u12,0,mu12,0,u3,0)be any ground state solution of(2.1),then The next steps are similar as we proof Theorem 2.1,for readers conveniences,we give the details here. Let(u12,0,mu12,0,u3,0)be any ground state solution of(2.1),then by strong maximum principle,we haveu12,0>0,u3,0>0. We claim To proof the claim,we consider the following system,whereµ1is replaced byµin system(2.1). The corresponding energy functional is given by It is easy to see Thus,there existst(µ)>0 such that wheret(µ)>0 satisfiesF(µ,t(µ))=0 andF(µ,t)is defined as following then by implicit function theorem, there existsδ> 0 such thatt(µ1) = 1,t(µ1)∈C1(µ1−δ,µ1+δ)and By Taylor expansion,we have thus, Since then,by(6.7)-(6.9),we have Thus,by(6.6a),(6.6c),we have Next,we prove Since(d1w,md1w,d3w)is a ground state solution of(2.1),we have Let then,by(6.10)and(6.11),we have Similar,we have Hence, Since(u12,0,mu12,0,u3,0)and(d1w,md1w,d3w)are both the ground state solution of(2.1),we obtain which implies that So Since(1.5)has a unique positive ground state solutionw,thus This completes the proof. Acknowledgements This paper was completed when M.Zhen was visiting the University of British Columbia.He is grateful to the members in the department of Mathematics at University of British Columbia for their invitation and hospitality.The research of J.Wei is partially supported by NSERC of Canada. The first author was partially supported by NSERC of Canada.


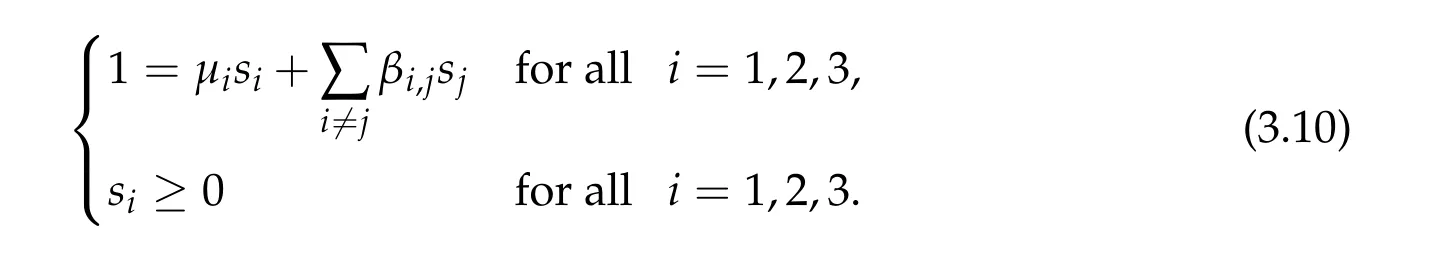

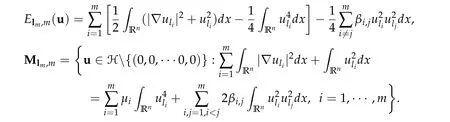


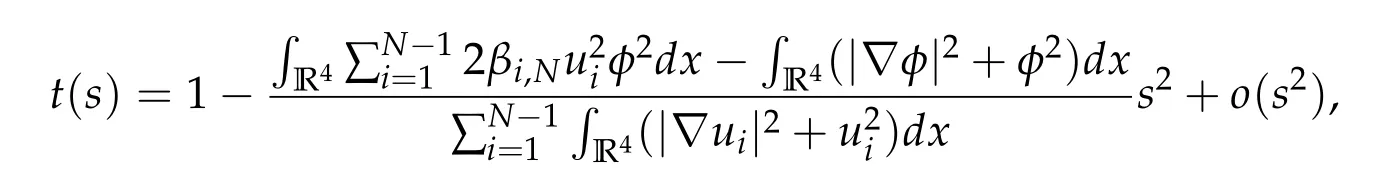

4 Proof of Theorem 2.1 and Theorem 2.4

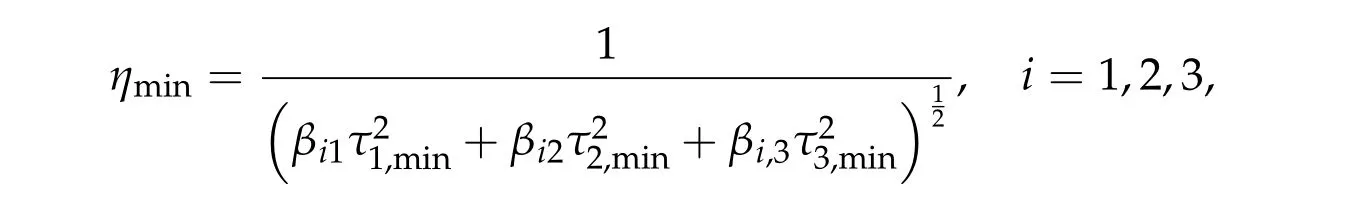
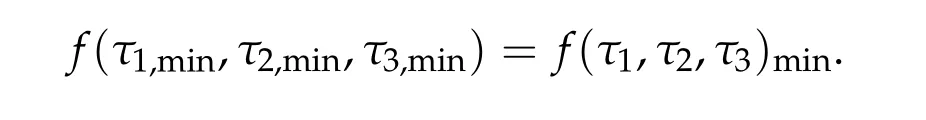

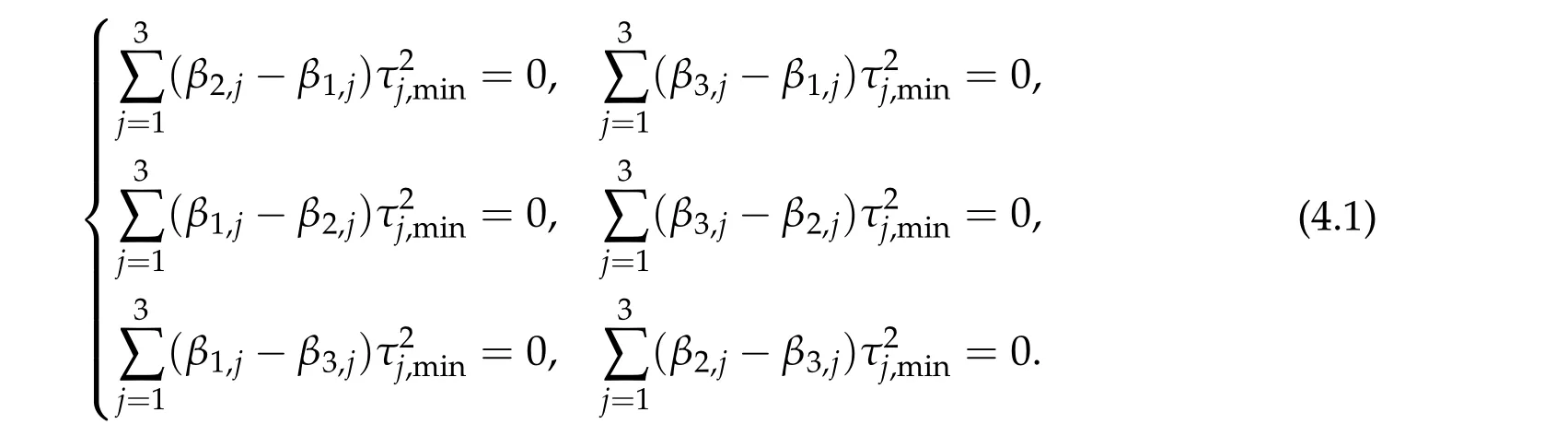




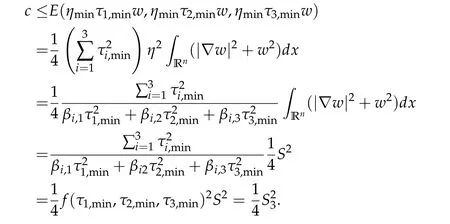
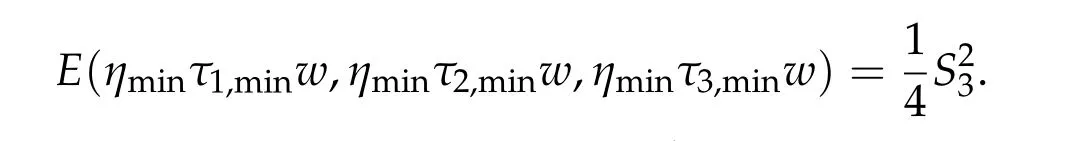


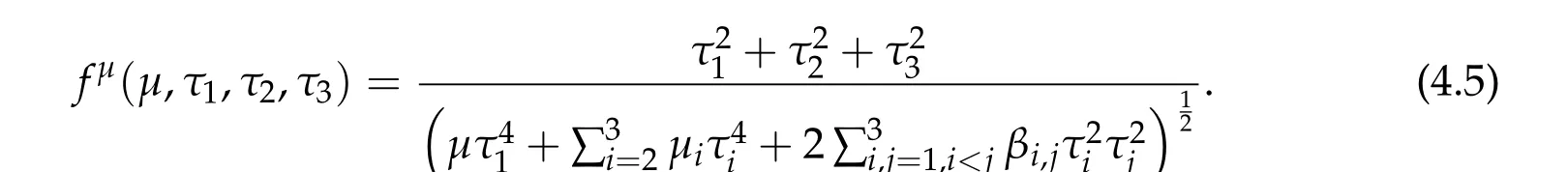

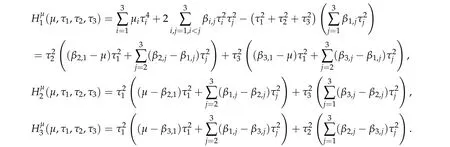
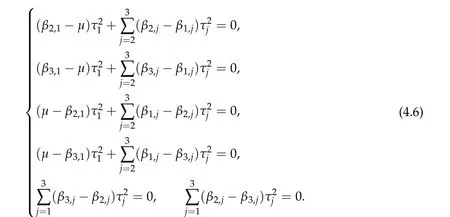
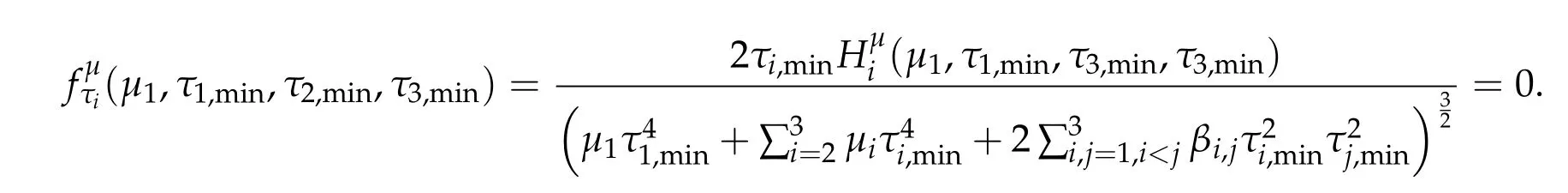
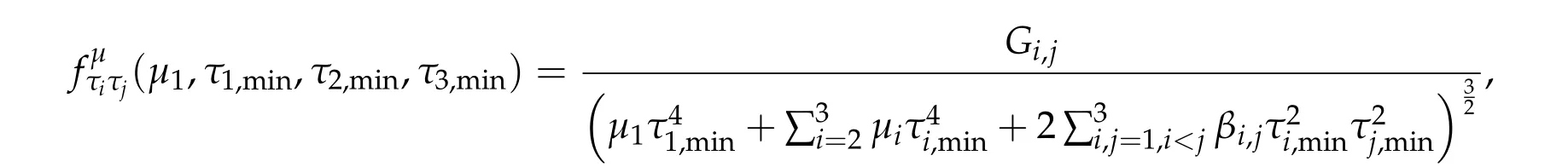

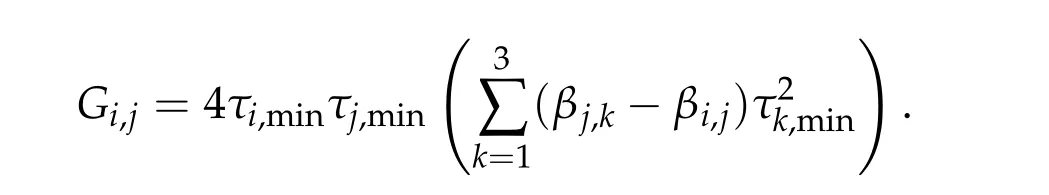
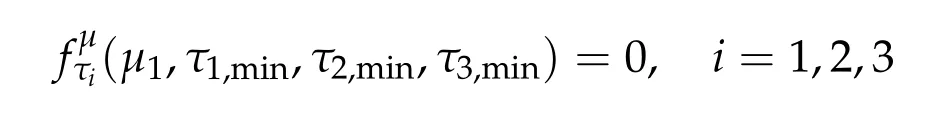
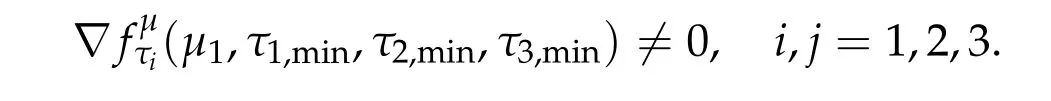
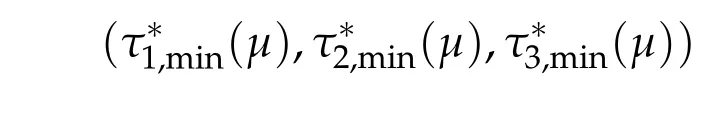

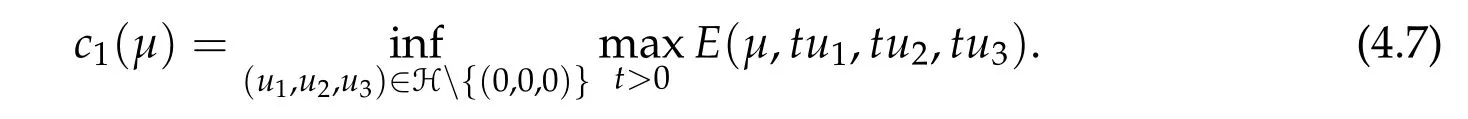
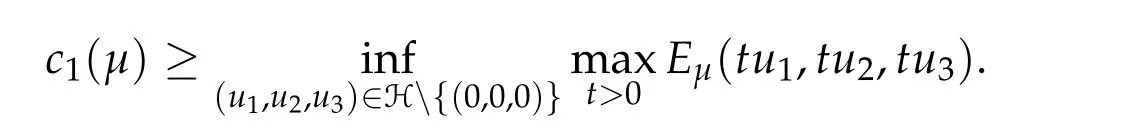

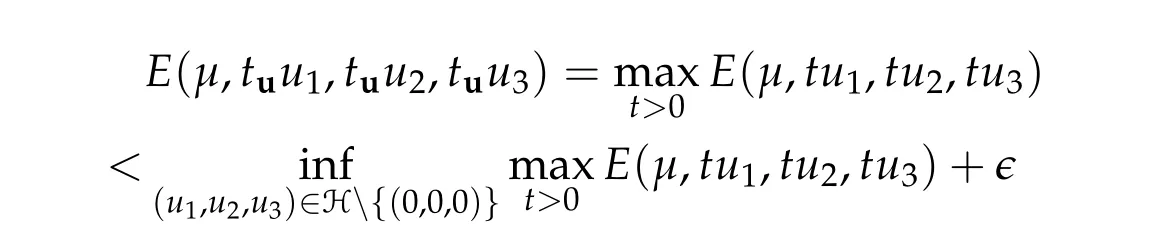
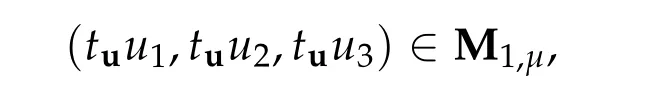
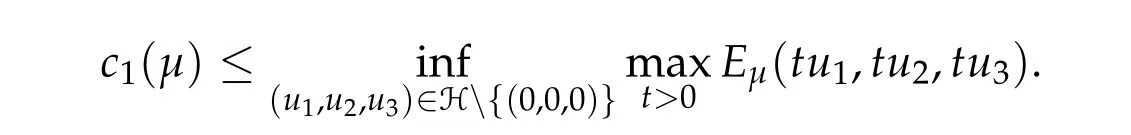

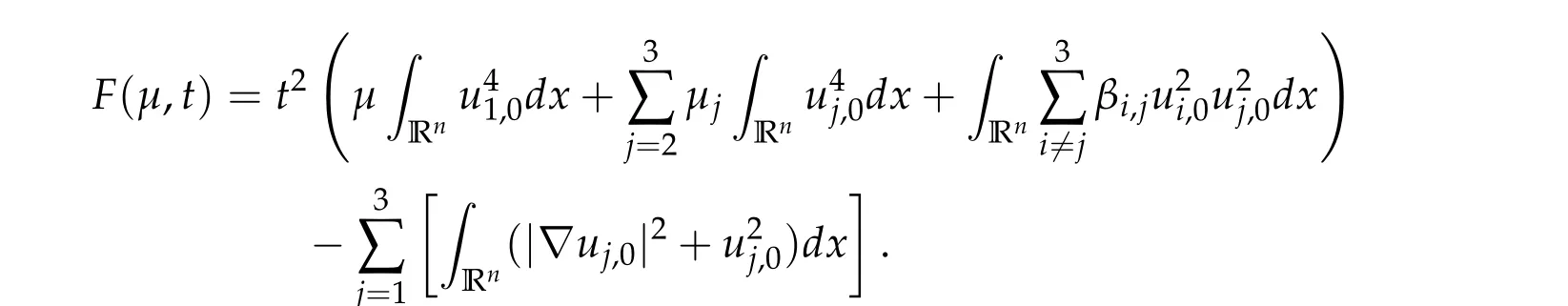


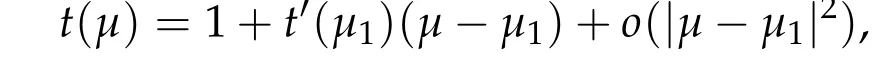

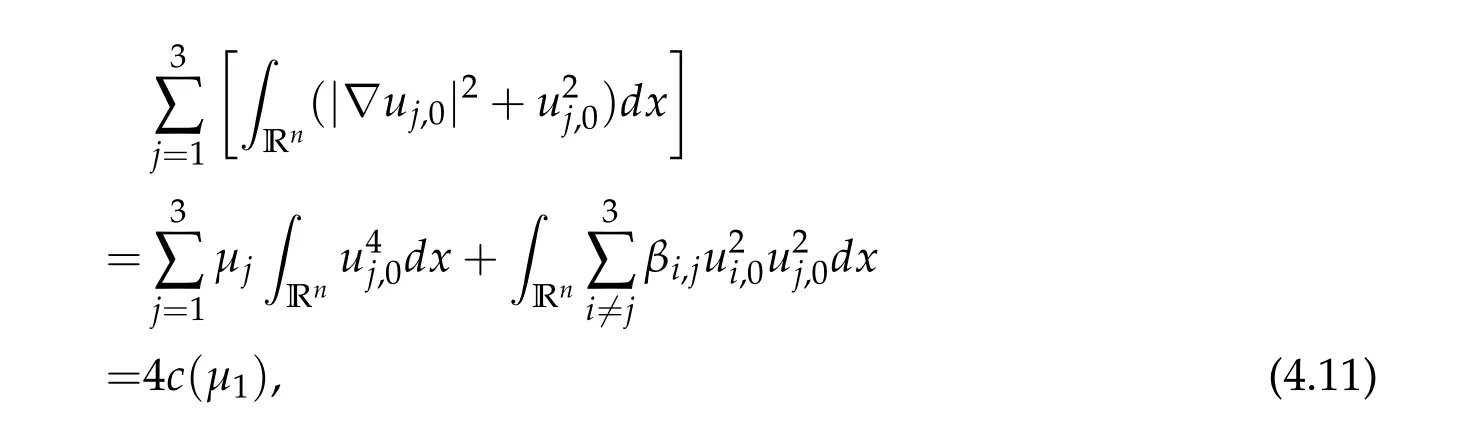
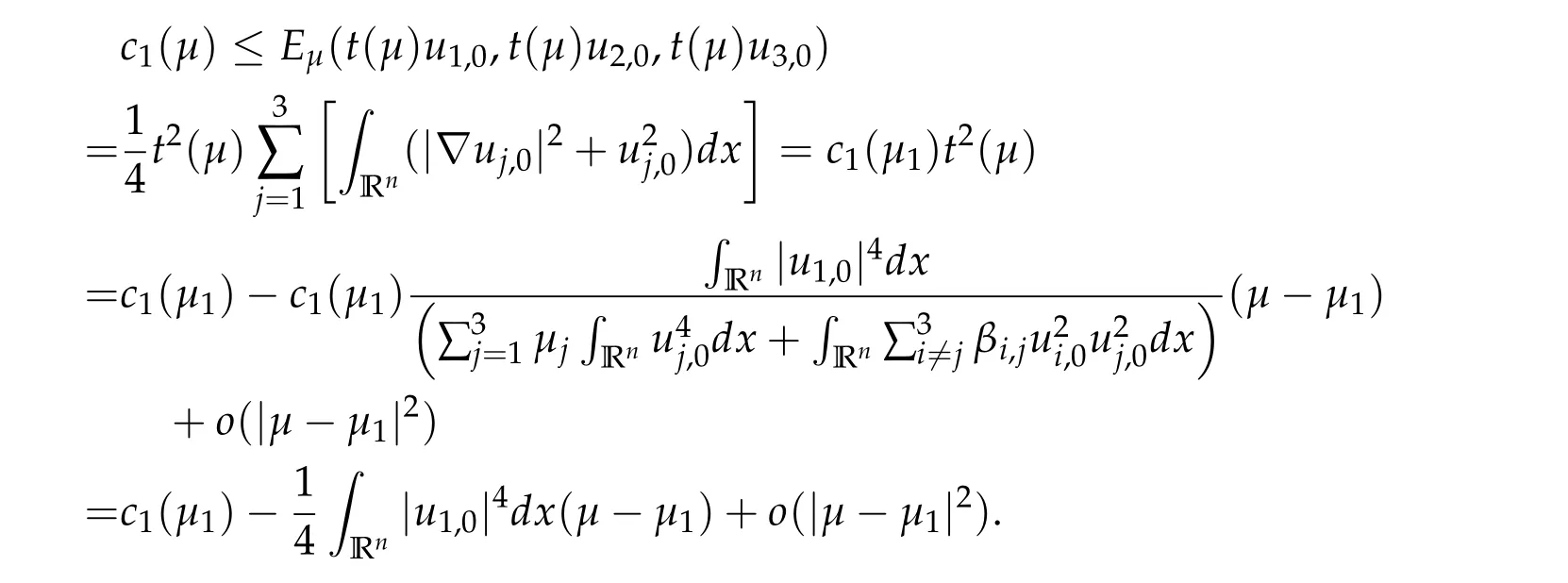


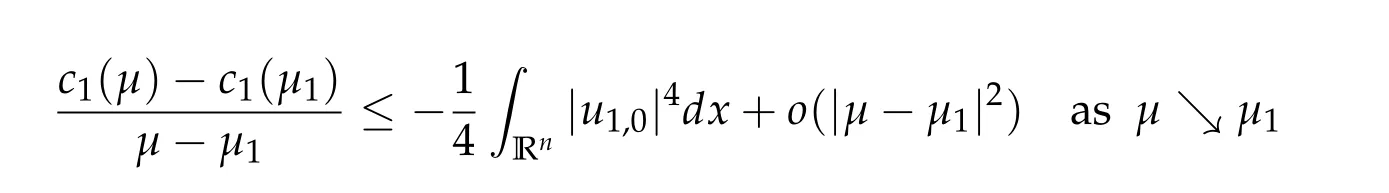
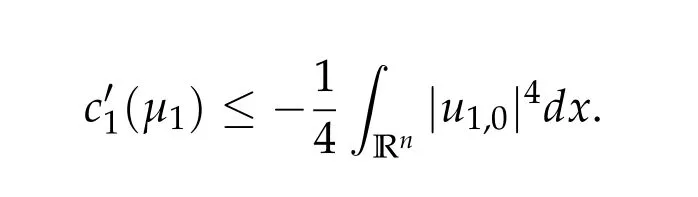




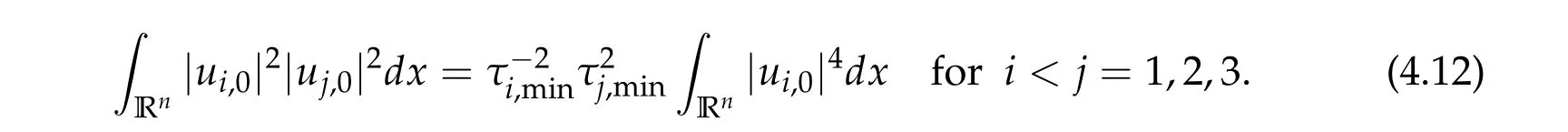
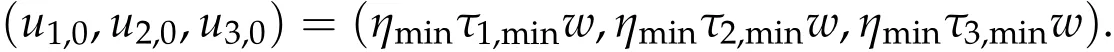
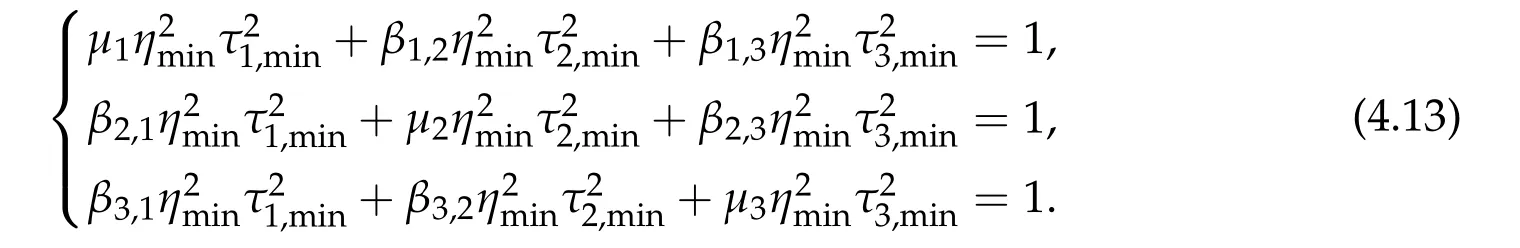

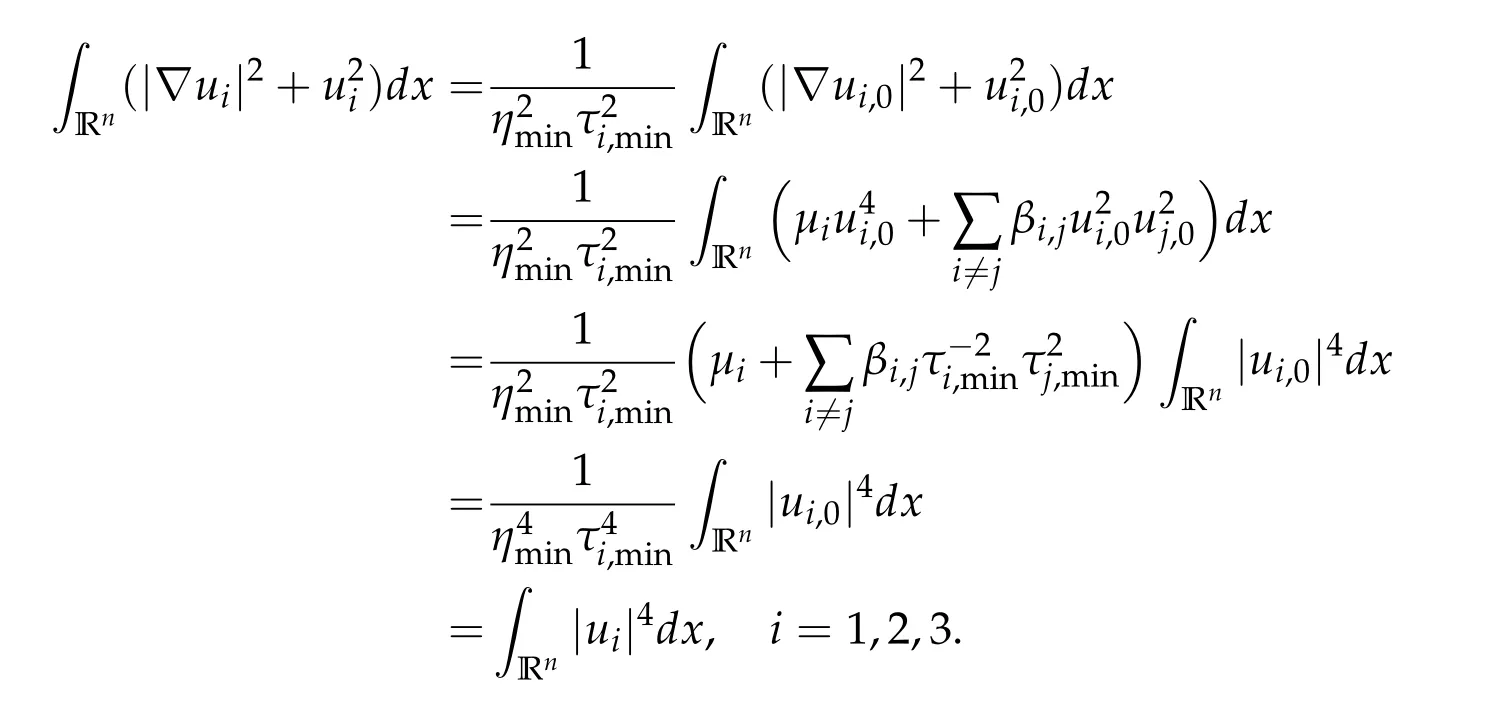

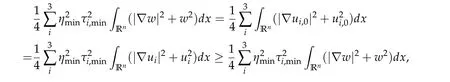
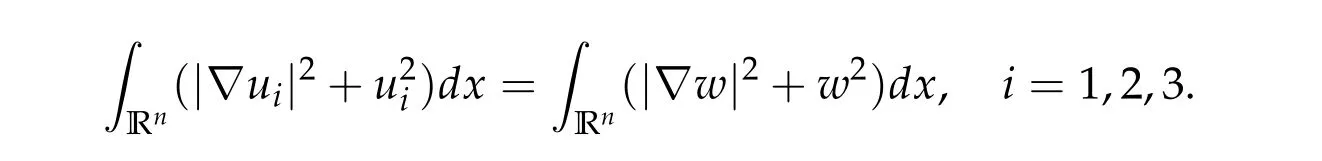

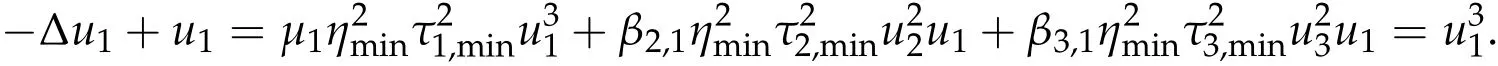
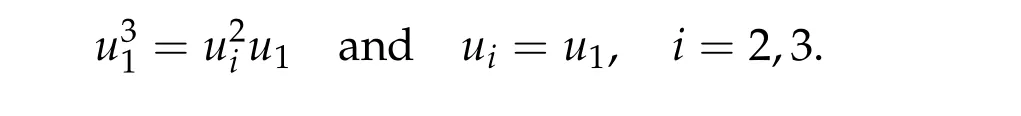
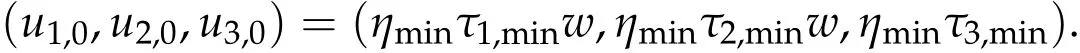
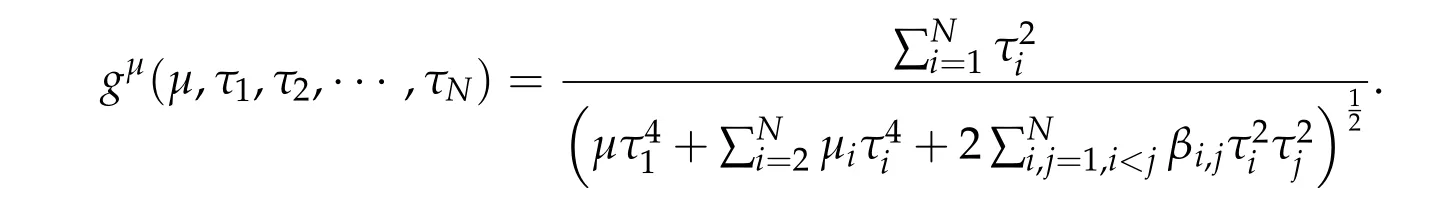

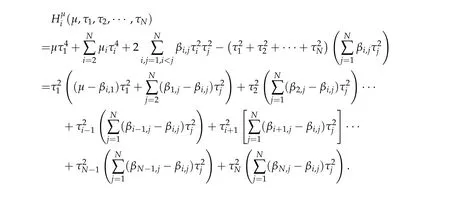
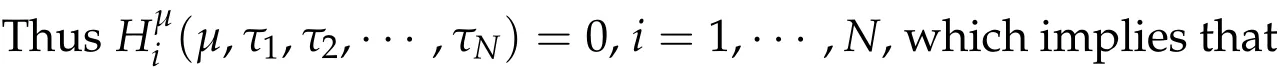
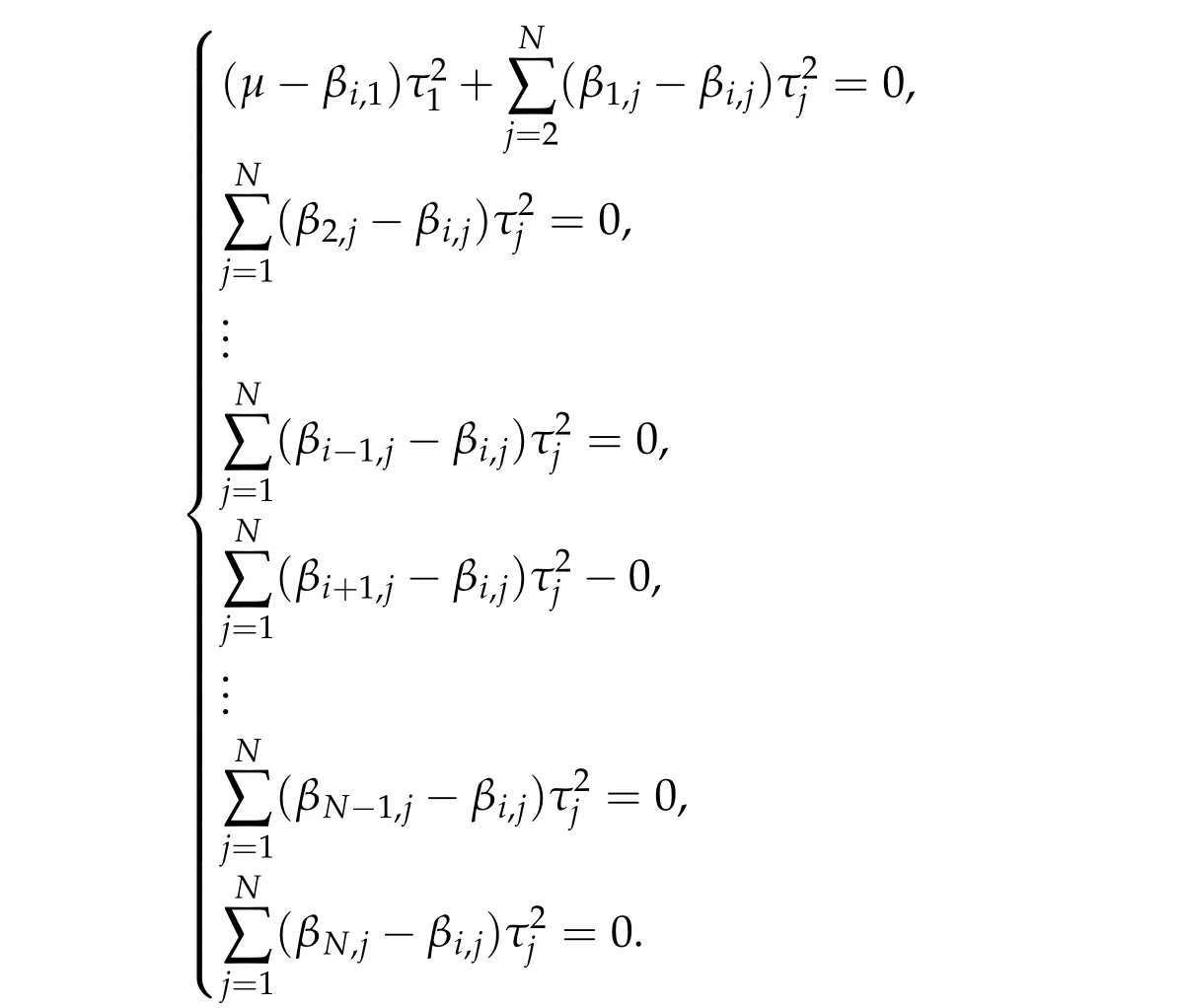
5 Proof of Theorem 2.2 and Theorem 2.5





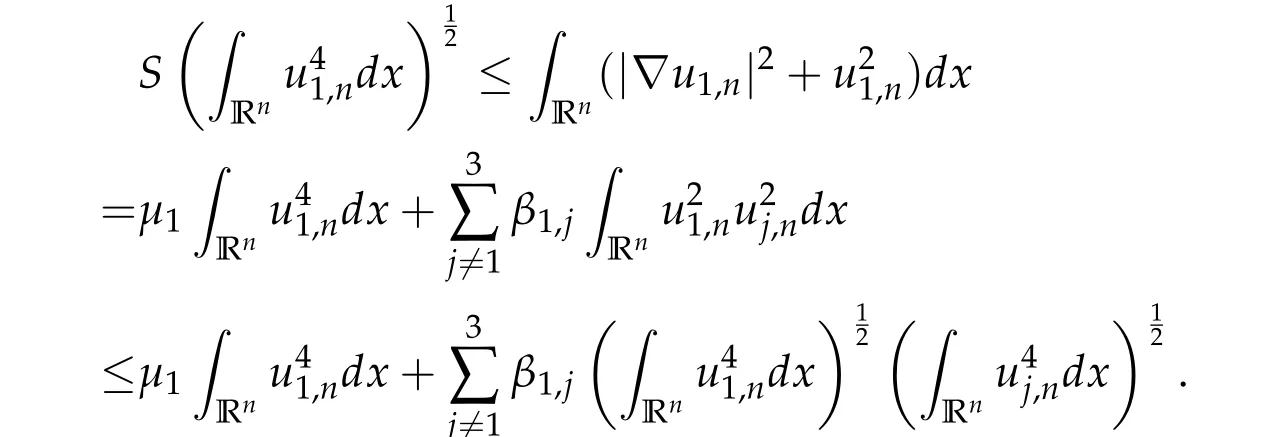

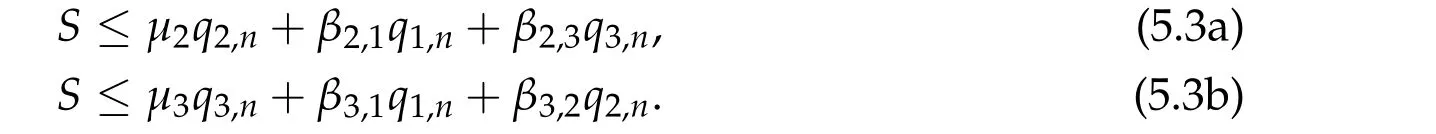

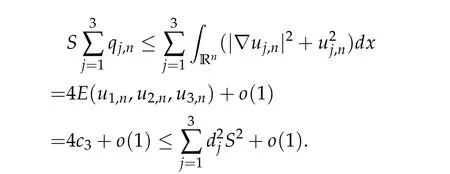

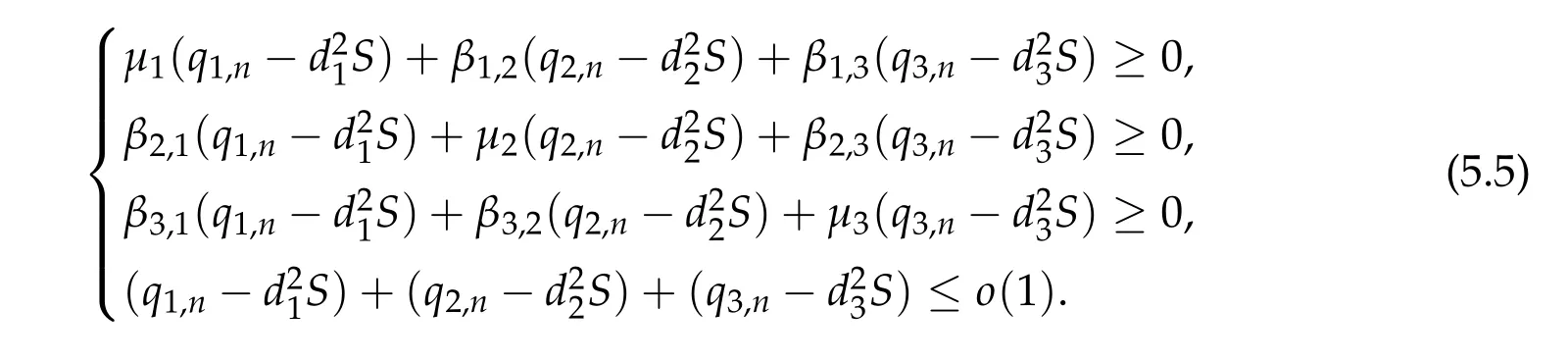




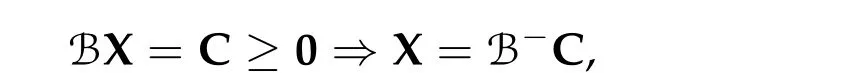


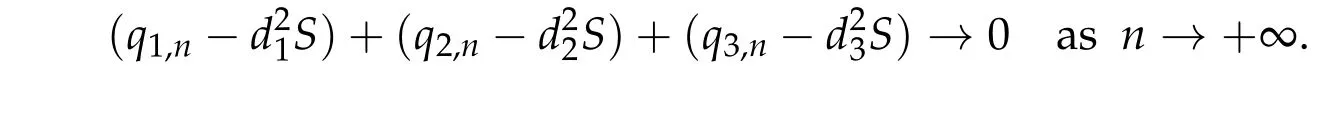






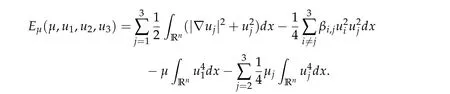

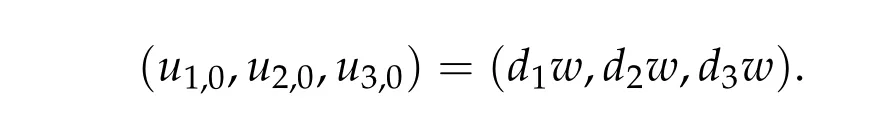
6 Proof of Theorem 2.3


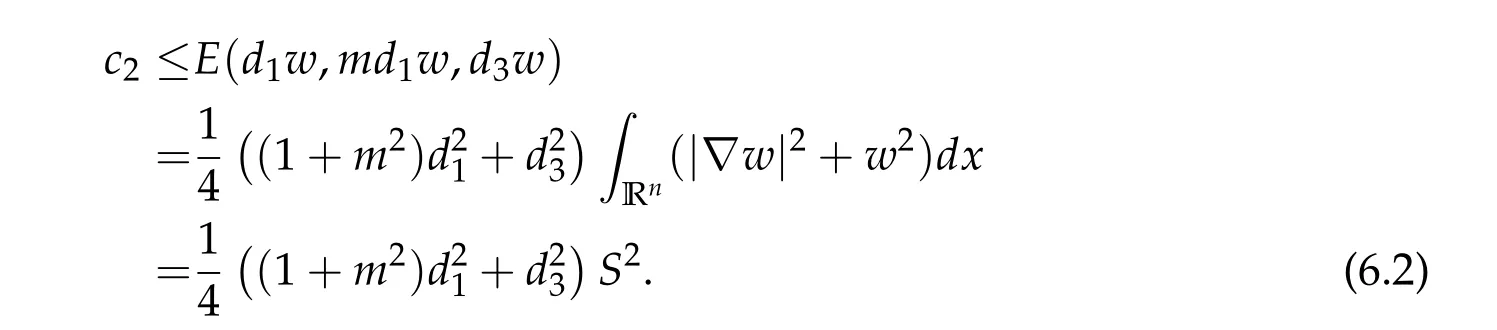
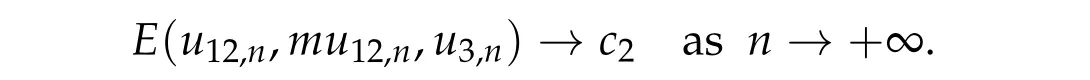
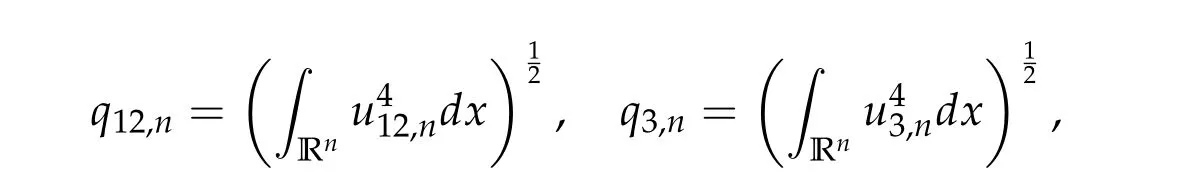

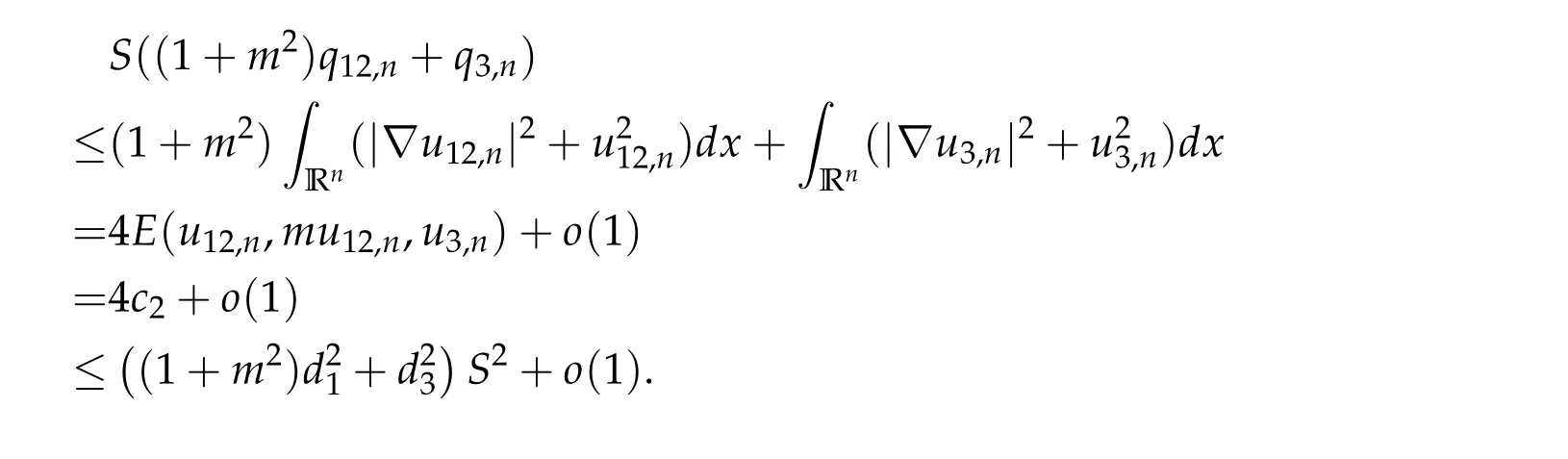

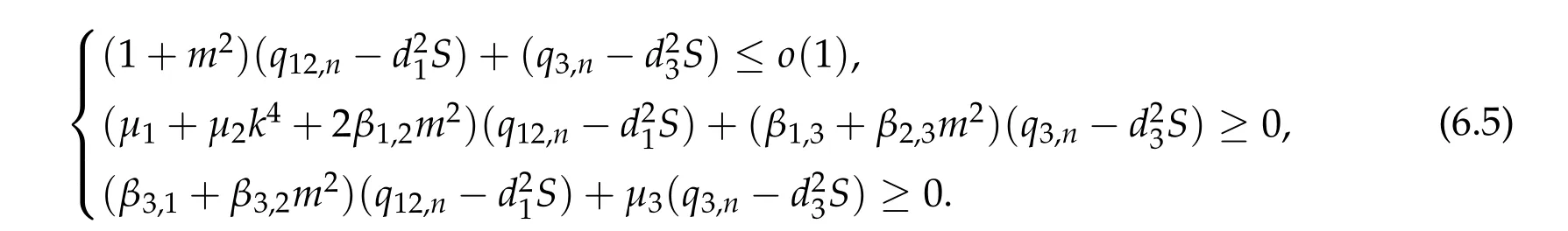

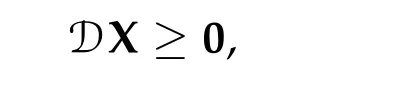

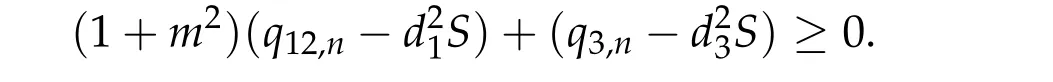
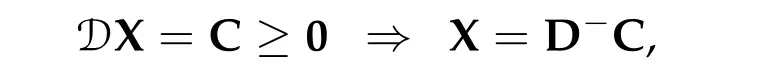


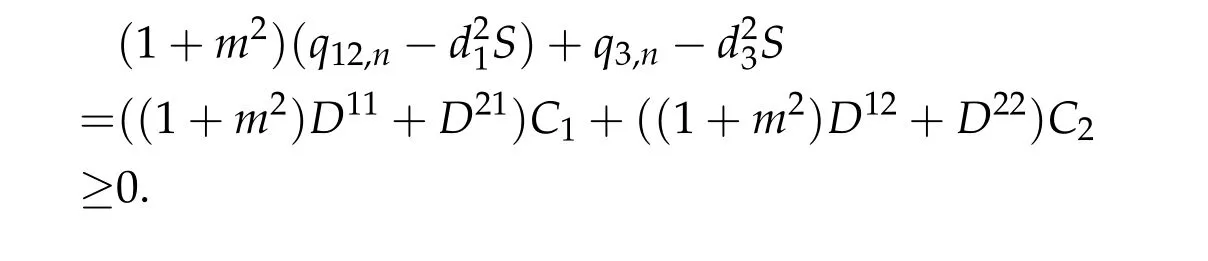


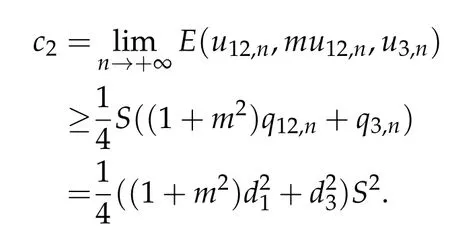
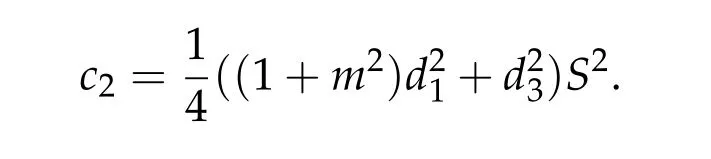
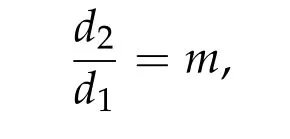
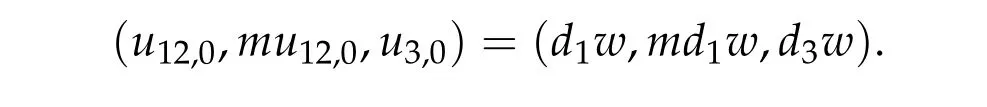
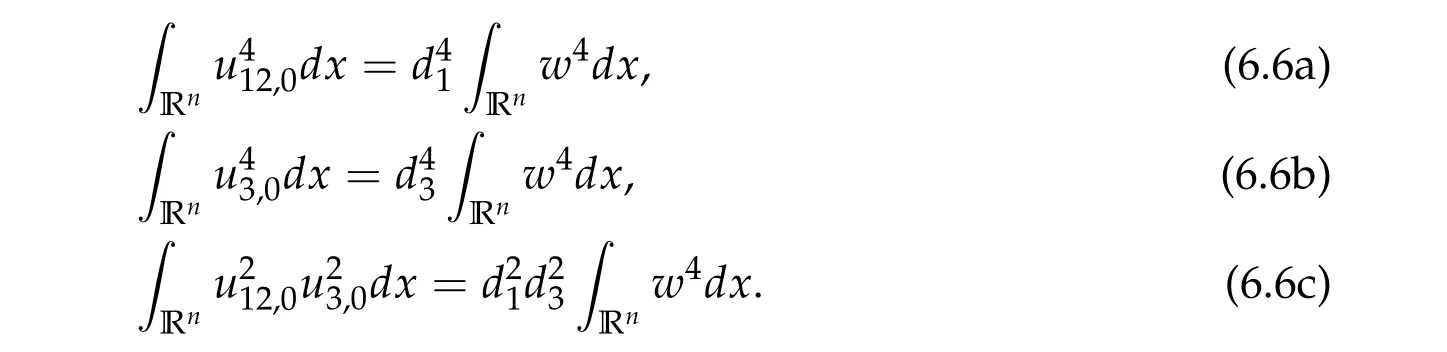

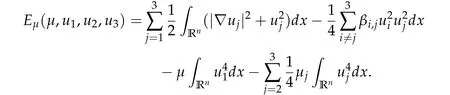
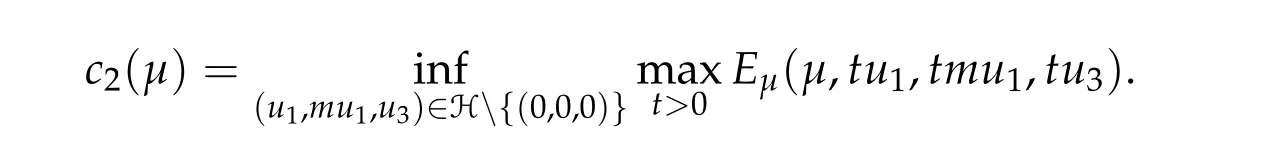



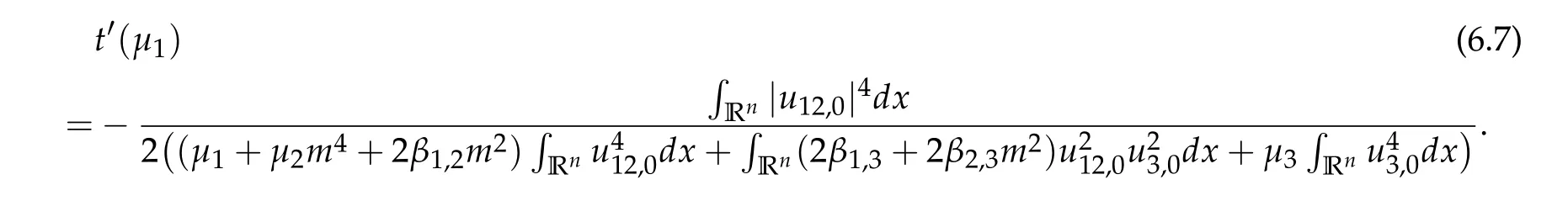


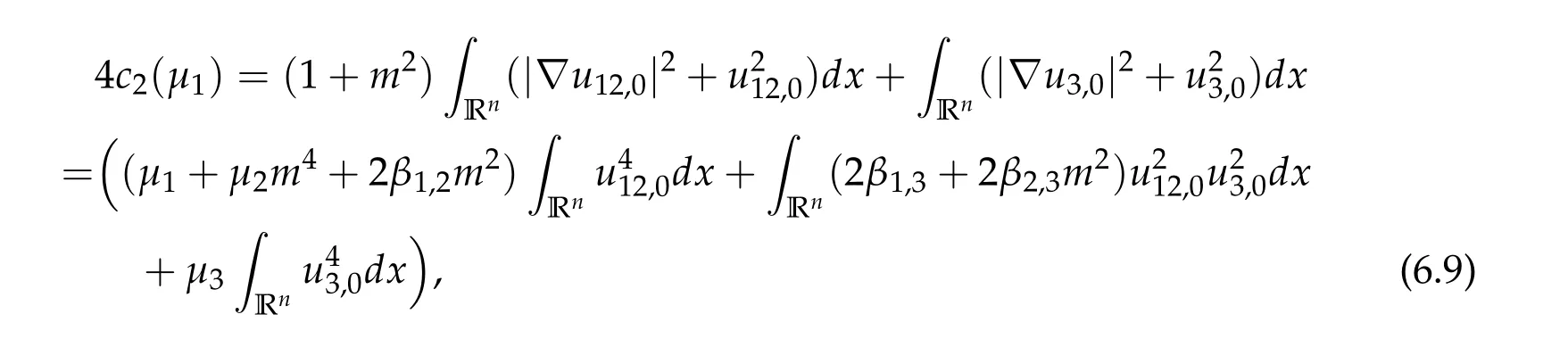

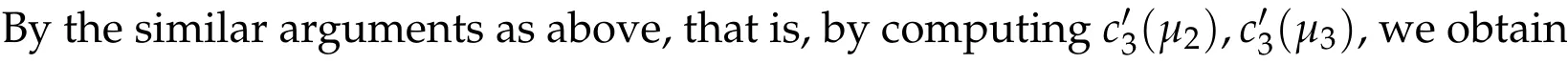


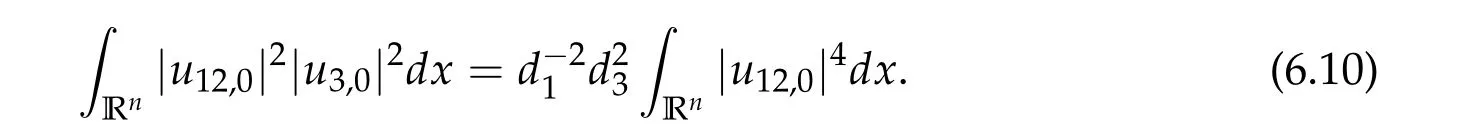
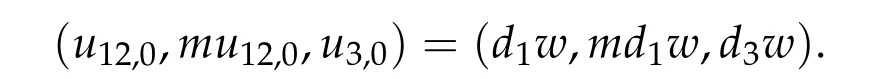
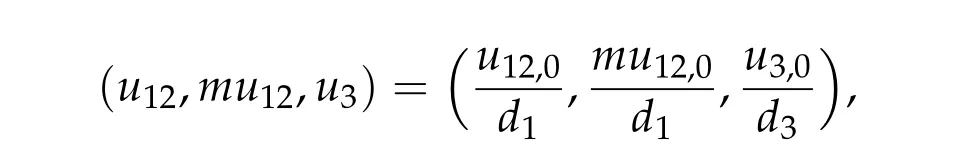
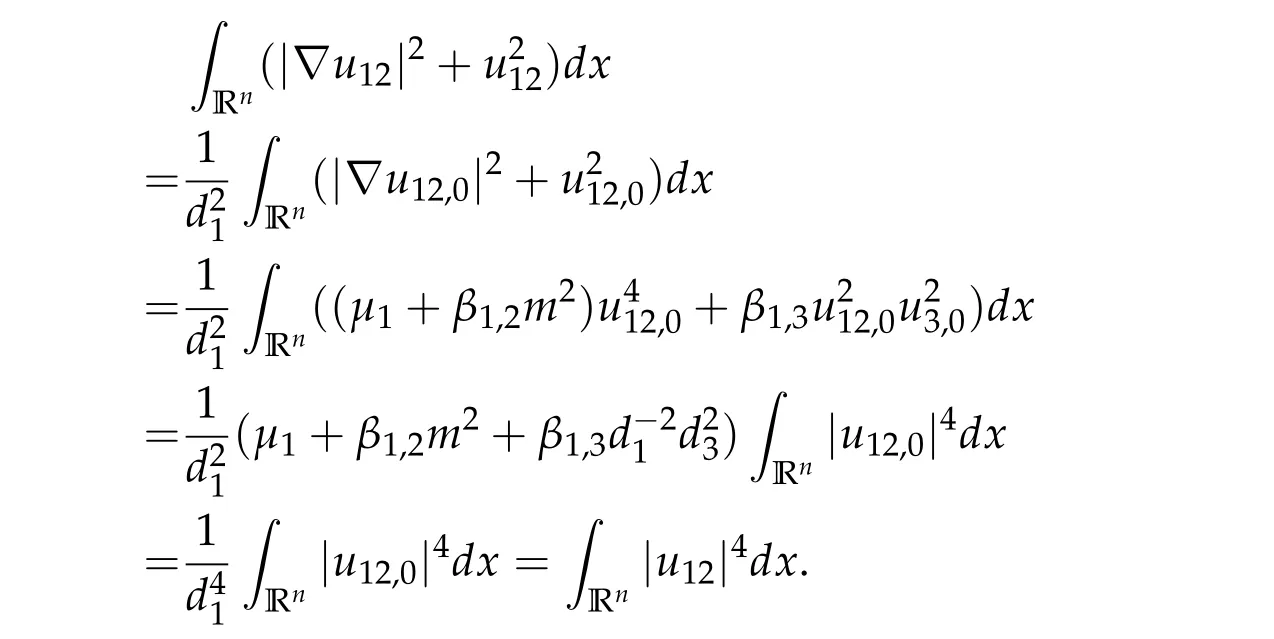
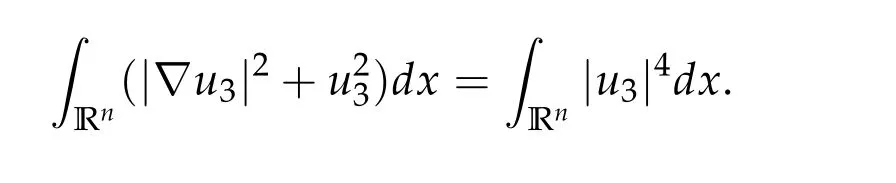
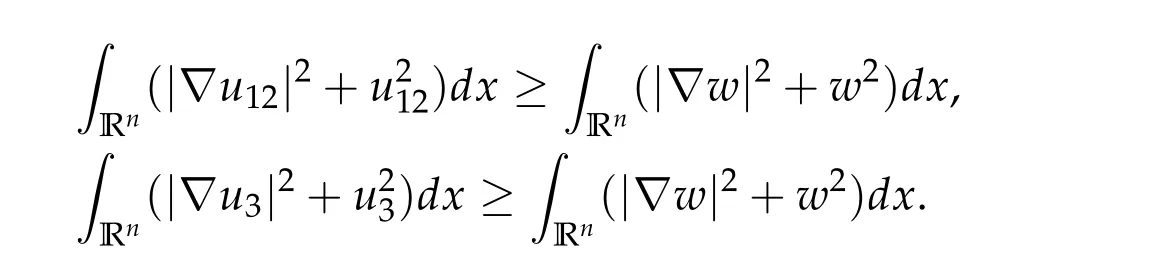
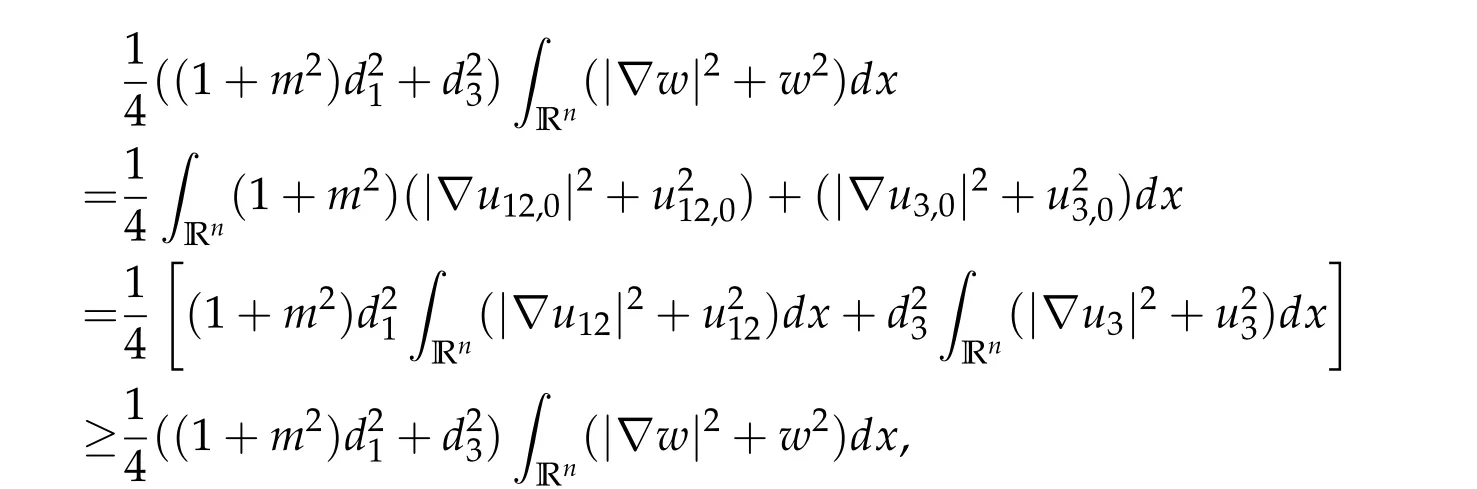
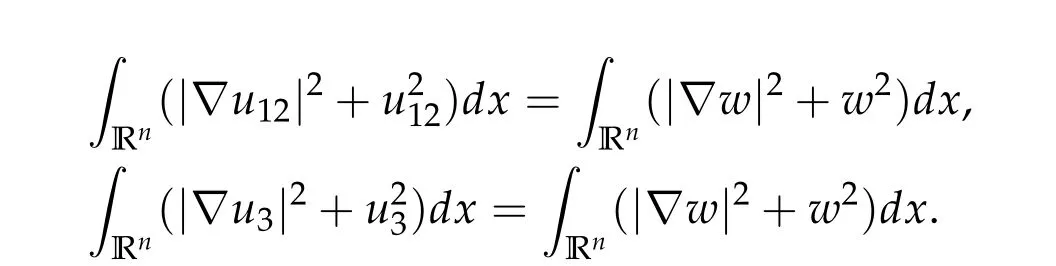

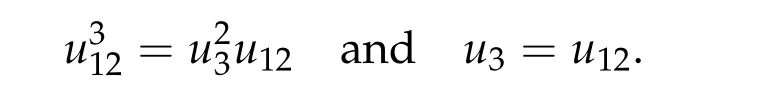
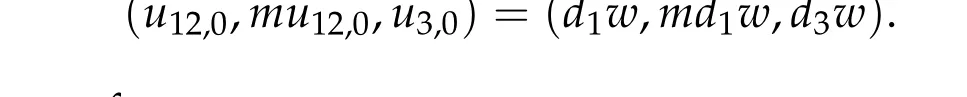
杂志排行
Analysis in Theory and Applications的其它文章
- Ground States to the Generalized Nonlinear Schrdinger Equations with Bernstein Symbols
- Index Iteration Theory for Brake Orbit Type Solutions and Applications
- Diffusion with a Discontinuous Potential: a Non-Linear Semigroup Approach
- Deformation Argument under PSP Condition and Applications
- Multiple Sign-Changing Solutions for Quasilinear Equations of Bounded Quasilinearity
- Ground States to the Generalized Nonlinear Schr¨odinger Equations with Bernstein Symbols
